基于方差分析与Logistic回归模型的公路交通事故率研究

刘亚洲

(招商局重庆交通科研设计院有限公司， 重庆 400067)

基于方差分析与Logistic回归模型的公路交通事故率研究

刘亚洲

(招商局重庆交通科研设计院有限公司， 重庆 400067)

为了能够对公路交通事故的发生进行有效控制，采用方差分析方法对交通事故率的相关因素进行统计分析，得知疲劳驾驶、车速、超载、道路几何线形、车道宽度、交通流、交通密度、交叉口间距和气象条件9个相关因素对交通事故率的影响较为显著。基于Logistic回归模型理论，建立交通事故率回归模型，定量分析各个影响因子对交通事故率的影响程度。结果表明：车道宽度、超载、车速、交叉口间距对交通事故率的影响程度最大。

交通事故；方差分析；Logistic；回归模型

随着高速公路建设的快速发展，我国高速公路交通安全问题成为研究的热点。在人-车-路-环境系统体系中，由于某因素条件的改变可引起交通事故的发生，因此应加强对公路交通事故率相关因素的探索与研究。景天然[1]依据大量交通事故数据与调查资料，分析了城市道路条件，包括交通饱和度、路面宽度、交叉口间距和交通量等，与交通事故率之间的关系。在交通事故率的相关因素研究过程中，一些研究学者分别从驾驶员、平面线形、气象条件、交通流等几方面对交通事故率进行了深刻研讨[2-7]。王洪明、陈斌等[8-9]对我国公路交通事故现状进行了特征分析，分析表明西部地区高速公路的交通事故仍呈增长趋势。这些研究中，仅仅只考虑了单因素对交通事故率的影响，且不清楚各个单因素对交通事故率的具体影响程度。因此，本文采用方差分析方法对交通事故率的相关因素进行统计分析时，首先面临的问题是对交通事故率的相关因素进行筛选，找出影响程度明显的几个因素，并将其作为代表变量，再利用这些主要影响因素对事故率进行回归分析，探讨其对事故率的综合影响。

1 交通事故率的相关因素

在人-车-路-环境道路体系中，根据专家调查法，可认为交通事故率的相关因素如表1所示。在获取交通信息前，需对其数据进行预处理，将定性或定量变量进行规范化，以便于后期对其建模。

表1 交通事故率的相关因素

由于影响交通事故的因素很多，一些因素可能对交通事故率的影响程度不够显著，且变量太多可能会给后期构建回归分析结果带来严重影响，因此，本文首先对交通事故率的影响因素进行显著性筛选，剔除那些影响不够显著的因素。下面采用方差分析方法对人(包括年龄、性别、疲劳驾驶及车速)、车(包括超载和制动性)、道路(包括道路几何线性、路面状况、车道宽度、交通流、交通密度及交叉口间距)、环境(包括气象条件和温度)4大类变量进行显著差异区分。

2 方差分析

方差分析[10]实质上就是对观测值的变异情况进行数量分析。从变异性角度出发，可将观测值的总变异分解为如下2部分：

1) 由各因素水平改变引起的变异，称为组间变异；

2) 由个体差异(随机因素、误差)引起的变异，称为组内变异。

实践表明，任一事物的影响因素很多，因此，要想辨别出交通事故率具有哪些显著性因素，且探索其显著因素的边际影响效应，是当前面临的主要问题。

变量X组间变异的计算公式为：

(1)

变量X组内变异的计算公式为：

(2)

变量X标准差的计算公式为：

(3)

式中：S是标准差；n为群组i和j数据个数的总和；n-1为整体数据的自由度。

将所有数据的离差平方和(SS)分解成组间的平方和(SSG)与误差平方(SSE)2部分，计算公式分别为：

SS=SSE+SSG

(4)

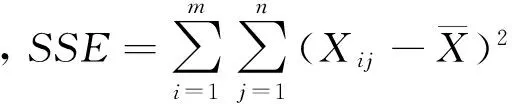
(5)

(6)

因此，可由式(3)计算出整体数据的均方差(平方和与自由度的比值)：

(7)

式中：MS为均方差；DF为自由度。

将总均方差分解为组间方差(MSG)和误差方差(MSE)2部分，并利用统计量F来表示自变量对因变量影响的显著性，计算公式为：

(8)

将该F值与统计分析得到的F值进行比较，若观测的F值大于理论值，则可认为各因素水平之间存在显著差异。

本文对重庆市某高速公路2011—2013年的交通事故信息进行了统计，对原始数据信息进行预处理后，应用STATA软件对其进行了方差分析，结果如表2所示。

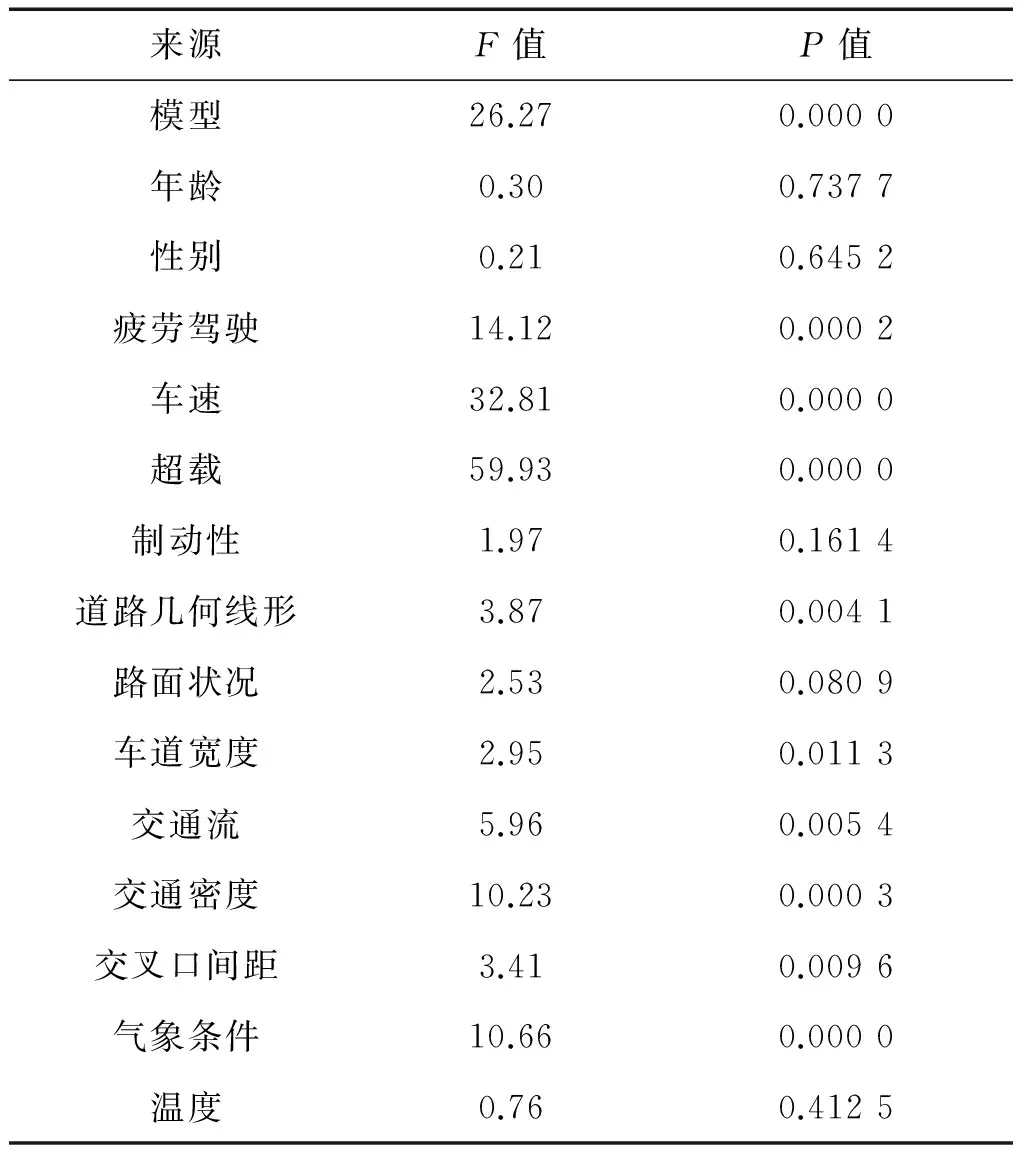
表2 方差分析结果

由表2可以发现，疲劳驾驶、车速、超载、道路几何线形、车道宽度、交通流、交通密度、交叉口间距和气象条件9个因子变量的概率P均小于0.05，表明9个因子变量对交通事故率的影响比较显著。

3 Logistic回归模型

3.1 模型建立

将交通事故看作二分因变量yi(yi=0表示该交通事故没有发生，yi=1表示该交通事故发生)，建立Logistic回归模型[11]，对因变量交通事故率和以上分类自变量进行回归分析。 每个事故案例中，各个自变量X=(X1,X2…,Xn)可以被认定为定量或定性变量，也可以被认为是连续或离散变量。 将第i个事故案例会发生的概率P(Yi)简写为Pi，记为：

Pi=P(yi=1|X1,X2,…,Xn)

(9)

二分类Logistic回归模型公式为：

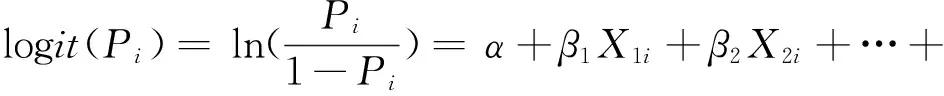
(10)

因此，可以计算Pi值：

(11)

式中：α为常数项；βi为回归系数，其代表解释变量与因变量的相关性。

通常，计算某事件发生的概率时应采用事件发生和不发生概率的比值作为参考指标，也称其为相对风险比，简称发生比。发生比的表达式为：

(12)

发生比率exp(β)是衡量相关因子变量对因变量事故率影响程度的重要指标。当因子变量每增加1个单位，因变量事故率将增加exp(βi)个单位。

3.2 结果分析

本文依托重庆市绕城高速公路G5001南彭镇至复盛镇段交通事故调查表，利用STATA对该路段在2011—2013年内的交通事故数据进行了多元Logistic回归，回归分析结果如表3所示。另外，对模型的拟合优度进行了ROC检验 ，ROC 检验值达到 0.75 以上,表明回归模型模拟效果较好。

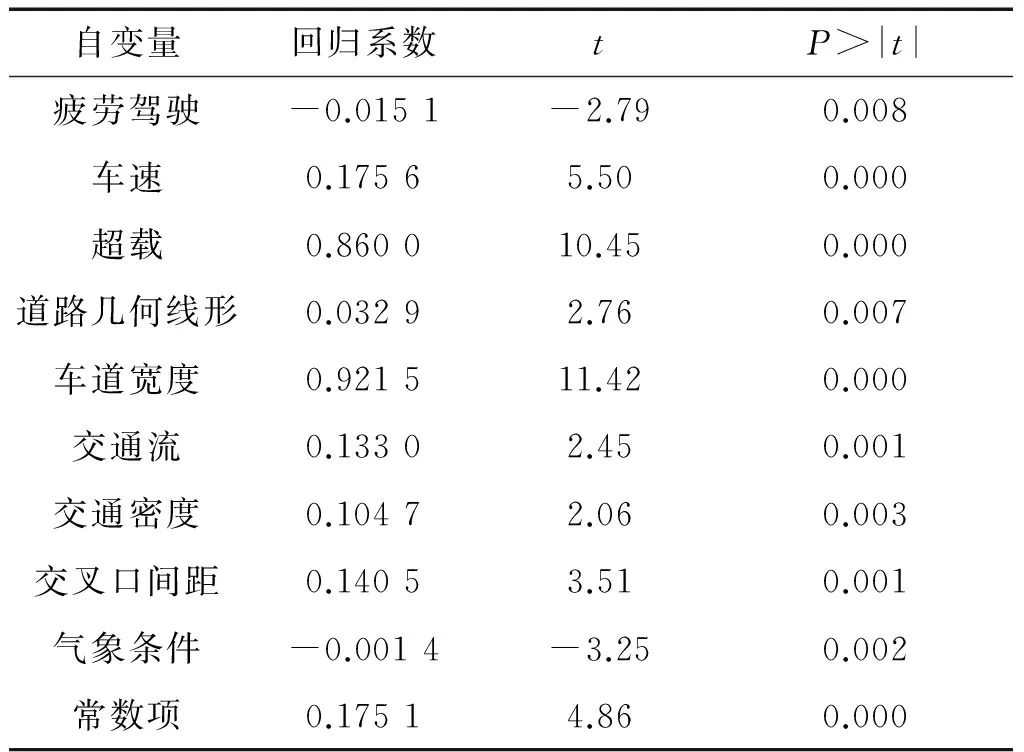
表3 Logistic回归模型结果

注：t为统计量。

由表3可知，车道宽度、超载、车速、交叉口间距、交通流是交通事故率的主要影响因素；车速每增加1个单位，其会致使交通事故率增加exp(0.175 6)个单位。

对交通事故数据进行多元Logistic回归时，将各自变量的回归系数代入Logistic回归模型中，可得：

4 结论

本文对交通事故统计数据中所采集的相关因素进行了方差分析，找出其影响显著的相关因素，并通过建立的Logistic回归模型对显著因素进行了Logistic回归分析，以观察各因素对因变量交通事故率的影响程度。基于本文研究,得出以下结论：

1) 对交通事故率具有显著影响的相关因素为疲劳驾驶、车速、超载、道路几何线形、车道宽度、交通流、交通密度、交叉口间距和气象条件。

2) 交通事故率的相关因素对其的影响程度大小排序为：车道宽度>超载>车速>交叉口间距>交通流>交通密度>道路几何线性>气象条件>疲劳驾驶。

3) 对于交通不安全或危险路段，可从车道宽度、超载、车速、交叉口间距、交通流等几方面采取相应的抢险措施，及时疏通交通。

4) Logistic回归模型可用于预测在不同因素条件下的交通事故率，进而评估某城市潜在危险路段的分布区域。

[1]景天然.城市道路条件与交通事故率的关系[J].同济大学学报，1992，20(3)：335-340.

[2]朱 嘉.对沪杭甬高速公路交通事故率影响因素的计量分析[J].公安大学学报(自然科学版)，2002(1):58-60.

[3]郭应时，付 锐，袁 伟，等.山区公路事故率与平面线形的关系[J].交通运输工程学报，2012，12(1):63-71.

[4]白永清，何明琼，刘 静，等.高速公路交通事故与气象条件的关系研究[J].气象与环境科学，2015，38(2)：66-71.

[5]陈雪梅，高 利，魏中华，等.驾驶员因素与交通事故率的关联性[J].北京工业大学学报，2007，33(7)：697-701.

[6]吴 勇，刘新荣，李 蕊.快速路分流区事故率与交通密度的关系[J].西南交通大学学报，2014，49(1)：134-140.

[7]吴 勇，刘新荣.快速路路段类别事故率与交通流状态关系[J].中国公路学报，2013，26(3)：150-157.

[8]陈 斌，袁 伟，付 锐，等.连续长大下坡路段交通事故特征分析[J].交通运输工程学报，2009，9(4)：75-84.

[9]王洪明.我国公路交通事故的现状及特征分析[J].中国安全科学学报，2009，19(10)：121-126.

[10]杨小勇.方差分析法浅析-单因素的方差分析[J].实验科学与技术，2013，11(1)：41-43.

[11]许月卿，田 媛，孙丕苓.基于Logistic回归模型的张家口市土地利用变化驱动力及建设用地增加空间模拟研究[J].北京大学学报(自然科学版)，2015，51(5)：955-964.

Study on Road Traffic Accident Rate Based on Variance Analysis and Logistic Regression Model

LIU Yazhou

In order to effectively control the occurrence of road traffic accidents,this paper pays uses the variance analysis method to statistically analyze the relevant factors of traffic accident rate,and the results showed that there are nine factors of fatigue driving,speed,overload,road geometry,lane width,traffic flow,traffic density,intersection distance and weather conditions have obvious influence to traffic accident rate. Based on logistic regression model,this paper sets up traffic accidents regression model to quantitatively analyze the influence degree of each influence factor to traffic accidents rate. Results show that lane width,overload,vehicle speed and intersection distance have the most significant influence on traffic accident rate.

road traffic accident; variance analysis; Logistic; regression model

10.13607/j.cnki.gljt.2016.06.031

2016-07-28

刘亚洲(1984-)，男，江苏省泗阳县人，本科，工程师。

1009-6477(2016)06-0144-04

U491.3

A