悬臂梁不同单元类型计算误差分析

张永超，佟丽莉，曹 婧,吕 晨

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；2.哈尔滨师范大学 数学科学学院，黑龙江 哈尔滨 150025)

悬臂梁不同单元类型计算误差分析

张永超1，佟丽莉1，曹 婧2,吕 晨1

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；2.哈尔滨师范大学 数学科学学院，黑龙江 哈尔滨 150025)

为了研究悬臂梁用不同单元类型计算应力结果与真实测量值的误差和该误差产生的影响因素。首先，用ABAQUS有限元软件对悬臂梁结构进行壳单元建模和实体单元建模，分别计算出Mises应力值，再用经典材料力学方法计算出相同情况下悬臂梁Mises应力值，然后用电阻应变测试法计算出悬臂梁的真实应力值，计算出各种应力计算方法相对于真实测量值的误差。最后，分别计算不同厚度悬臂梁，用壳单元和实体单元分别计算出的Mises应力值，将实体单元计算应力值代替真实测量应力值，得到壳单元计算结果相对于实体单元计算结果的相对误差。研究结果表明，悬臂梁用实体单元计算出的Mises应力值相对于壳单元更加接近于真实测量值。随着悬臂梁厚度的增加，壳单元计算结果的精度越来越小。对于同一厚度的悬臂梁，不同位置处壳单元计算应力值对于真实值的相对误差近似为一常数。

悬臂梁；壳单元；实体单元；Mises应力；相对误差

在实际工程中，对于薄壁结构进行数值模拟时，人们将薄壁结构简化为壳单元进行计算的方法被广泛应用到各个行业[1]。虽然这种壳单元的简化可以大大提高计算效率，但是由此带来的计算误差往往不能被忽视。因此很有必要对不同单元类型数值模拟的工程问题进行误差分析,以达到既能提高计算效率又能满足工程精度的要求[2]。对于数值模拟分析中，用不同单元类型进行模拟，国内外学者开展了大量的研究工作。中南大学的张雅鑫等[3]用数值模拟的方法对泵车壁架进行多种单元类型的计算，得到用壳单元和实体单元对泵车壁架进行简化计算的结果相对于真实结果偏小，并且用实体单元进行简化的结果更接近于真实值。邱智学等[4]利用ABAQUS对一受话器播脚采用不同的壳单元类型进行了有限元分析和比较,并用ANSYS软件的模拟结果进行检验。本文分别通过壳单元，实体单元和经典材料力学方法对悬臂梁受弯应力进行计算，计算结果与实际测量值进行对比得到各种计算方法的误差值。再用实体单元模型的计算结果代替真实测量值，通过对不同厚度的悬臂梁进行壳单元数值模拟分析，进一步探讨了壳单元计算悬臂梁的误差影响因素。

1 计算过程及方法

1.1 悬臂梁结构尺寸和实验方案

1.1.1悬臂梁结构尺寸

试验用悬臂梁结构如图1，截面尺寸分别为30 mm×30 mm、23 mm×23 mm的薄壁悬臂梁模型的几何参数，及施加的载荷如表1。材料为202不锈钢，材料的弹性模量2.3×105MPa、密度7 850 kg/m3、泊松比0.29、屈服强度≥345 MPa、抗拉强度490～630 MPa。

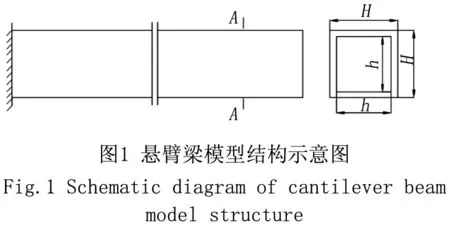
表1 悬臂梁模型几何参数

悬臂梁号H/mmh/mm悬臂梁长度l/mm端部载荷F/N悬臂梁一3028.41000100悬臂梁二2322100040

1.1.2实验方案

测试点分布如图2，在距离固定端尺寸分别为30，60，100，200，...，900 mm等共计选取11个测试点，应变片贴在悬臂梁受拉面对称中心线上。

应变片粘贴之前要将粘贴表面磨光并擦拭干净，保证应变片不会在测量过程中发生脱落的现象，挤出应变片下的气泡和过量胶水，贴好的应变片要保证胶层均勾、位置准确、无气泡和整洁干净。应变片贴片前后以及接线前后都要使用万用表进行检测，确保线路连接正确，避免虚接、损坏等问题。

1.2 ABAQUS计算过程

1.2.1实体单元

材料参数：弹性模量为203 000 MPa;密度为7 850kg/m3;泊松比为0.29。

边界条件为固支：U1=U2=U3=UR1=UR2=UR3=0

载荷为Y方向集中力：FY=-100 N

网格：网格尺寸2 mm；网格形状为六面体结构化网格；单元类型C3D8R八结点线性六面体单元。

1.2.2壳单元

材料参数：弹性模量203 000 MPa;密度7 850kg/m3;泊松比0.29;壳厚度0.8 mm。

边界条件为固支：U1=U2=U3=UR1=UR2=UR3=0

载荷为Y方向集中力：FY=-100 N

网格：网格尺寸2 mm；网格形状六面体结构化网格；单元类型S4R四结点曲面薄壳或厚壳。

1.2.3材料力学计算方法

实际工程中，悬臂梁发生横力弯曲较为常见，横力弯曲不仅有正应力，而且还有切应力，由于切应力的作用，横截面才会发生翘曲，平面假设不成立。但是经过理论分析证明，对于跨度与横截面高度之比大于5的细长梁，可以简化成不考虑横力弯曲的形式，材料力学公式仍然适用。

取悬臂梁上表面中心线上一点作为研究对象

根据材料力学中第四强度理论(形状改变比能理论)：

(1)

通过平面应力状态应力圆分析法得到下式：

(2)

σy=σz=0,再根据切应力互等定理：τyz=τzy=τxz=τzx=0

得：

(3)

又σmax=σx

(4)

所以得：

(5)

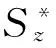
2 计算结果和分析

2.1悬臂梁1结果分析

根据悬臂梁1有限元实体单元和有限元壳单元模型计算结果，最大Mises应力分别为136.8、130.9 MPa,均靠近悬臂梁固定端。

在有限元模型中找出与实测点相同位置的Mises应力，得到实体单元计算值、壳单元计算值、材料力学计算值，以及实体单元计算值、壳单元计算值、材料力学计算值分别对实验值相对误差，相对误差绝对值平均值如表2所示，计算值和实验值的对比曲线如图3。

表2表明，对于实体单元模型，各测试点对于实验值的应力相对误差都在10%以内，平均相对误差为4.824%，小于5%，满足工程要求；对于壳模型，各测试点相对于实验值的应力相对误差都在20%以内，平均相对误差为9.088%，小于10%，和实际测量值误差较大；对于材料力学计算方法所得出的结果，各测试点相对于实验值的应力平均相对误差为26.879%，与真实值的误差最大。可见，用有限元软件做悬臂梁受弯构件所得的弯曲应力比用材料力学计算方法做悬臂梁受弯构件所得的弯曲应力更为准确。有限元实体单元比壳单元更适合悬臂梁的应力计算。

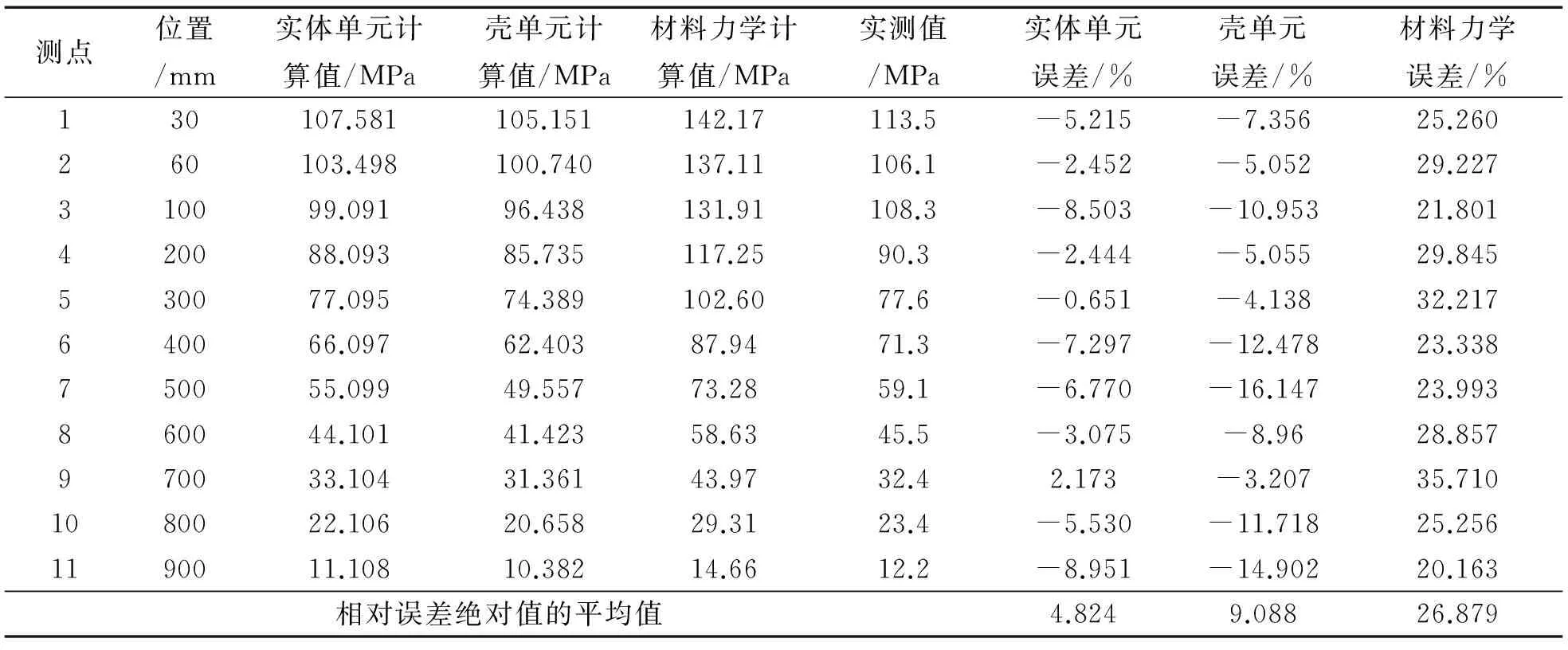
表2 悬臂梁1的不同计算方法计算值及相对误差

表3 悬臂梁2各种计算方法计算值及相对误差

2.2悬臂梁2结果分析

根据悬臂梁2的有限元实体单元和有限元壳单元模型计算结果，最大Mises应力分别为147.3、119.3 MPa,均靠近悬臂梁固定端。

在有限元模型中找出与实测点相同位置的Mises应力，得到实体单元计算值、壳单元计算值、材料力学计算值，以及实体单元计算值、壳单元计算值、材料力学计算值分别对实验值相对误差，相对误差绝对值平均值如表4所示，计算值和实验值的对比曲线如图4。

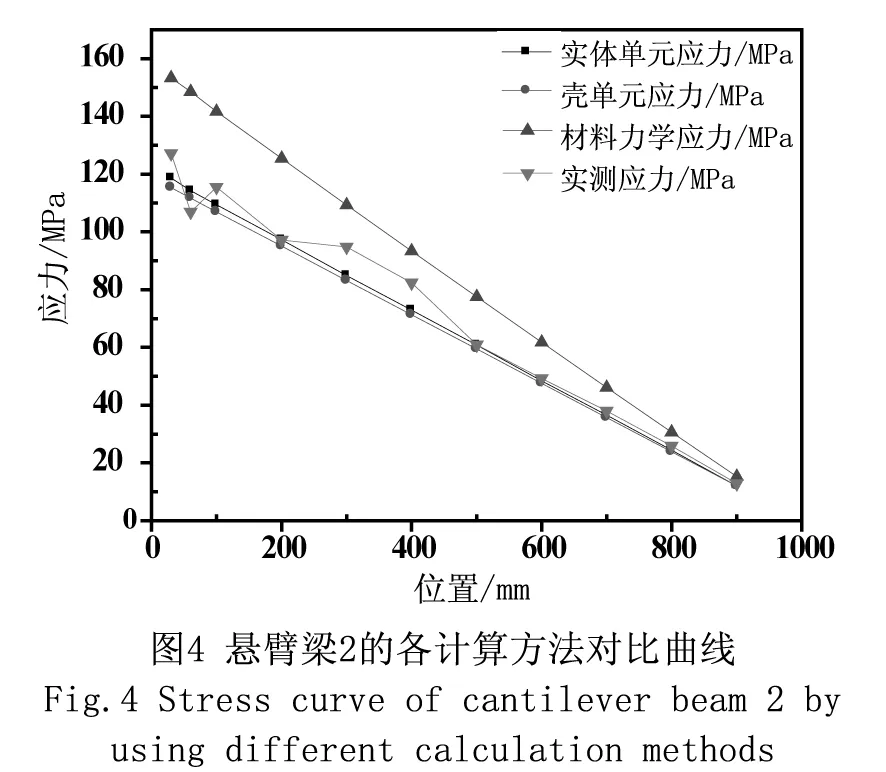
表3表明，对于实体单元模型，各测试点对于实验值的应力平均相对误差为4.337%，小于5%，满足工程要求；对于壳单元模型，各测试点相对于实验值的应力相对误差都在20%以内，平均相对误差为6.869%，小于10%，和实际测量值误差较大；对于材料力学计算方法所得出的结果，各测试点相对于实验值的应力平均相对误差为22.786%，与真实值的误差最大。可见，用有限元软件做悬臂梁受弯构件所得的弯曲应力比用材料力学计算方法做悬臂梁受弯构件所得的弯曲应力更为准确。有限元实体单元比壳单元更适合悬臂梁的应力计算。验证了对悬臂梁1计算所得的结论。

2.3不同壁厚悬臂梁计算结果分析

为探究壳单元计算悬臂梁受弯应力与真实值的相对误差的影响因素，设置长度为1 000 mm，厚度T分别为0.2、0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0 mm的悬臂梁，截面如图5所示。

根据以上讨论，用实体单元应力计算结果与实际测量值误差不到5%，所以可以用实体单元的应力计算结果代替实际测量值。分别用壳单元和实体单元计算不同厚度悬臂梁，距固定端200、400、600、800 mm处的Mises应力值，得到表4。

表4 不同厚度悬臂梁在不同位置壳单元相对实体单元误差表 单位：%

根据上表所得数据，得到距固定端相同位置处，不同厚度的悬臂梁用壳单元计算应力值相对于用实体单元计算应力值的误差曲线，如图6所示。同时也得到了，同一厚度，距固定端不同位置处的悬臂梁用壳单元计算应力值相对于用实体单元计算应力值的误差曲线，如图7所示。

由表4、图6和图7可知，不同厚度的悬臂梁，用壳单元计算应力结果相对于实体单元计算应力结果的误差是不同的。随着悬臂梁厚度的增加，误差值也随之增大。这是因为随着壁厚的增加，模型不能忽略截面法线方向的正应力，就不能再用壳单元来近似计算，也就是说壳单元更加适用于薄壁模型。

对于同一厚度的悬臂梁，用壳单元数值模拟的应力值相对于用实体单元数值模拟应力值的相对误差，在距固定端不同位置处近似为一常数。

3 结论

1)用不同单元类型对悬臂梁进行数值模拟分析，应力计算结果精度是不一样的。用壳单元和实体单元对悬臂梁进行数值模拟的结果相对于真值偏小，其中壳单元的误差较大，结果精度低；实体单元误差小于5%，结果精度高，满足工程要求。

2)悬臂梁壁厚对用壳单元数值模拟悬臂梁受弯应力的精度有影响，随着悬臂梁厚度的增加，计算精度随之降低。

3)对于同一厚度的悬臂梁，用壳单元数值模拟的应力值相对于用实体单元数值模拟应力值的相对误差，在距固定端不同位置处近似为一常数。

[1]CAE应用联盟 张建伟.ABAQUS 6.12有限元分析从入门到精通[M].北京：机械工业出版社, 2015.

[2]高广军, 田红旗, 姚 松.有限元三维实体单元与壳单元的组合建模问题研究[J].中国铁道科学, 2002, 23(4):52-54.

[3]张雅鑫.泵车臂架有限元多种单元计算的比较研究[D].长沙：中南大学, 2014.

[4]邱智学, 黄菊花, 谢世坤,等.ABAQUS壳单元在有限元分析中的应用研究[J].模具技术, 2003(5):9-11.

[5]林 芳, 鄂大辛, 张敬文.单元类型对有限元计算弯管截面畸变及壁厚变化的影响[J].精密成形工程, 2012(3):10-13.

(责任编辑 李军)

Calculation error analysis of cantilever beam of different element types

ZHANG Yongchao1,TONG Lili1,CAO Jing2,LV Chen1

( 1． College of Aerospace and Civil Engineering，Harbin Engineering University，Heilongjiang Harbin 150001，China; 2． College of Mathematical Sciences，Harbin Normal University，Heilongjiang Harbin 150025，China)

To study the error of calculated stress results and real measurement values of the cantilever beam with different element types and the its influencing factors, firstly, ABAQUS finite element software was used to model the shell element and solid element, and the stress value of Mises was calculated. Then the classical mechanics of materials method was used to calculate the same cantilever beam under Mises and the resistance strain test method was used to calculate real cantilever stress values. Finally, the shell element and the solid element of different thickness of the cantilever beam were used to calculate the Mises stress value. The results show that the Mises stress value calculated by the solid element is more close to the true value than the shell element. With the increase of the thickness of the cantilever beam, the accuracy of the calculation results of the shell element is getting smaller and smaller. For the same thickness of the cantilever beam, the relative error of the calculated stress value of the shell element at different position of the shell element is a constant.

Cantilever beam; shell element; solid element; Mises stress; relative error

1673-9469(2016)04-0005-05

10.3969/j.issn.1673-9469.2016.04.002

2016-08-01

国家自然科学基金资助项目(S2014GAT013)

张永超(1993-)，男，安徽滁州，硕士，从事先进复合材料与智能结构的研究。

TG333.17

A