基于铁路有效路径的换乘方案快速搜索方法
苏焕银,史峰 ,张佩,魏堂建,3
(1.中南大学 交通运输工程学院,湖南 长沙 410075; 2.郑州铁路局,河南 郑州 450052;3.华东交通大学 轨道交通学院,江西 南昌 330013)
基于铁路有效路径的换乘方案快速搜索方法
苏焕银1,史峰1,张佩2,魏堂建1,3
(1.中南大学 交通运输工程学院,湖南 长沙 410075; 2.郑州铁路局,河南 郑州 450052;3.华东交通大学 轨道交通学院,江西 南昌 330013)
研究铁路旅客换乘方案的快速搜索方法可为铁路售票系统提供支持。通过分析铁路旅客出行路径特征,引入非最短系数概念,给出有效路径的判定条件,设计有效路径的搜索算法。基于有效路径集,设计前序弧数法搜索任意计划出发时间的旅客最优换乘方案。整体算法由2个部分组成,一是整个铁路网络有效路径的预先生成和存储;二是给定计划出发时间和起讫站点的最优换乘方案的快速搜索。算法既考虑了铁路旅客的出行路径特征又突出了“快速搜索”的特点。基于2014年中国高速铁路网络及运行图进行算例分析,结果显示算法具有较高的运算效率和很强的实用性。
铁路运输;换乘方案;有效路径;非最短系数;运行图
铁路运输是旅客中长距离出行的重要交通方式,具有节能环保、安全舒适、可持续发展的明显优势。随着铁路客运网络的扩大以及居民生活水平的提高,旅客对铁路客运服务提出了更高的要求。旅客换乘方案的搜索既是协助旅客购票的铁路客运服务,又是基于列车时空网络进行客流分配的核心技术,在铁路旅客运输组织中具有重要意义。目前对换乘方案的研究一般以时间、费用、里程等为多目标构建数学规划模型[1],通过构造换乘网络,求解最短路获得最优解。崔炳谋等[2]通过匹配列车发到站间的衔接关系得到所有可行的出行方案,根据目标权重对方案排序得到K优解。杨信丰等[3]考虑最大换乘次数的限制,建立铁路旅客乘车方案优化模型,设计旅客出行可行路径的快速搜索算法。林冬梅等[4]提出换乘节点匹配法,在换乘次数的限制下通过匹配列车发到站间的衔接关系,等到始发终到站间所有可行出行方案。史峰等[5]设计了多种类型的换乘网络,并对各换乘网络的规模、功能和计算能力进行了综合比较分析。在出行路径搜索方面,传统的路径搜索方法是从起点开始,从各个方向不断向周围扩展,直到终点,背离终点方向的搜索为无效搜索,搜索规模较大。Hart等[6]提出的A*启发式算法,通过估价函数可引导搜索向着成本最小的方向进行,提高了最小费用路径搜索效率,但是对于铁路旅客特有的出行行为特征不能很好地描述,是具有一般应用性的路径搜索方法,针对性不强。对铁路路径选择的研究主要侧重于客运经由的计算,大多遵从“里程短、换乘次数少”的原则[7]。王华等[8]以接算站为点集构造网络缩小路网规模,考虑换线数来模拟换乘数,设计以距离与换线结合为单目标的启发性算法求解客运径路。吕晓艳等[9]提出一种车次约束机制下的径路生成计算方法:采取车站特殊径路的分布式存取与径路公共信息的全路共享的方式, 有效压缩径路信息存储空间,并通过车站特殊径路计算和公共径路计算生成有效径路。DOU等[10]基于列车时刻表构建了旅客换乘网络,考虑广义费用和列车剩余能力搜索路径。
铁路旅客换乘方案搜索主要在售票过程或售票模拟过程中实施运用,采用传统方法不能满足快速搜索的需求。随着售票过程的进展,一些列车区段相继满员,列车时空网络变得越来越支离破碎。在这种不断变化的网络中搜索当前最优换乘方案时,如何既考虑铁路旅客的出行路径特征又突出“快速搜索”的特点,是本文研究的核心内容。铁路网络中,任意2点之间旅客经常出行的路径一般是确定的,这样的路径具有2个特征,一是绕道里程不会太长,二是一般不会出现迂回节点。旅客根据实时信息,选择最优的换乘方案,而且,旅客的选择空间是有限的,更确切地说是局限于常用的几条路径上。因此,大可不必从全路网的范围内搜索旅客出行的最优换乘方案,可以将搜索范围限制于常用的几条路径上,既符合旅客的出行行为特征,又可以避免大量的无效搜索工作,提高换乘方案的搜索效率,实现快速搜索的目的。本文通过引入非最短系数概念,给出有效路径(旅客经常出行的路径)的判定条件。设计具有能力约束的时空换乘网络,将换乘方案的搜索范围限制在有效径路上,并设计了前序弧数法,基于有效路径集快速搜索任意计划出发时间的旅客最优换乘方案。整体算法由2个部分组成,一是整个铁路网络有效路径的预先生成和存储;二是给定计划出发时间和起讫站点的最优换乘方案的快速搜索。基于2014年中国高速铁路网络及运行图进行算例分析,验证了算法的正确性和高效性。
1 铁路旅客换乘方案及费用分析

铁路旅客换乘方案是指从始发站u出发,换乘几趟列车后,到达终点站v的乘车序列,可表示为
(1)
其中,“+”表示列车区段之间的换乘衔接,当m=1时,该换乘方案表示直达方案;当m>1时,表示需要换乘不同的列车。

(2)


2 铁路旅客有效路径
2.1 有效路径定义
铁路网络中任意两点之间旅客经常出行的几条路径称为有效路径。有效路径通常有2个重要特征:1)绕道里程不会太长;2)仅当需要换乘或列车折返时才可能使得路径上出现重复节点。

(3)
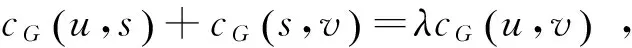

综上所述,有效路径R的判定条件如下:
(4)

图1 有效路径搜索范围示意图Fig.1 Hunting zone diagram of effective paths
2.2 有效路径搜索
在式(4)判定条件的约束下,可以在式(3)的范围内搜索出多条有效路径。注意到“最短路上任意两点之间的路径也是最短路”,有效路径也具有类似特征“有效路径上任意2点之间的路径也是有效路径”。基于此特征,设计有效径路的搜索算法。



图2 有效路径搜索方法示意图Fig.2 Search method diagram of effective paths
算法1 有效路径的搜索算法
开始
对于k=2,3,…,n,循环执行
开始1
当m 开始2 返回2 返回1 结束 3.1 有效路径上列车区段的判定法则 图3 列车路径与有效路径不一致的示意图Fig.3 Train section doesn’t lie on an effective path (5) 3.2 基于单条有效路径搜索换乘方案 方便描述起见,构造沿有效路径R进入或离开车站s的列车区段集: (6) (7) 算法2 基于单条有效路径的换乘方案搜索算法 开始 开始1 开始2 返回2 返回1 结束 运算量较大的运算为语句: (8) 综上所述,算法2只要适当加强预处理,就是一个关于有效路径内乘车区段数的线性复杂度的最优算法。 3.3 基于多条有效路径搜索换乘方案 算法2所描述的是基于单条有效路径搜索换乘方案的方法,注意到不同有效路径之间可能存在重叠部分,基于多条有效路径搜索换乘方案时,将公共部分共享搜索,则可进一步提高搜索效率。 4.1 基础数据及参数标定 采用2014年7月1日运营的高铁线路及列车时刻表(独立于路网的线路除外)。路网节点由444个列车停靠站组成,路网弧段为相邻两站间铁路线路,站间里程为弧段里程。车站划分为4个等级,如表1所示。设置列车票价为0.45元/km,疲劳因子为0.5元/min,调整出发时间惩罚因子为0.4 元/min。考虑到高铁网络比较简单,设置每对O-D间的最多有效路径数M=2,非最短系数λ=1.7。 表1 不通车站等级的参数设置Table 1 Parameter settings for different station classes 4.2 程序运行结果及分析 算法代码采用C#语言编写,运行环境是CPU双核、主频为3.20 GHz,内存为4G的计算机。算法运行分为2部分:1)加载基础数据并计算任意2站间有效路径,将有效路径存储;2)在给定计划出发时间及始发终到站的条件下,实时搜索最小费用换乘方案。第1部分平均耗时50 s,第2部分运行时间不超过0.1 s,算法具有很高的求解速度。 4.2.1 有效路径分析 选取两个具有代表性的出行O-D,计算有效路径,结果如表2所示,具体的路径节点分布如图4所示。南京南至上海虹桥的2条有效路径确实是旅客经常出行的路径,符合旅客的出行行为特征。其实,蚌埠南至武汉还有第2条路径:蚌埠南→滁州→南京南→全椒→合肥→麻城→武汉,图4中虚线部分的子路径(蚌埠南→滁州→南京南→全椒→合肥)的里程为329 km,而对应的最短路(蚌埠南→淮南东→合肥)的里程为132 km,那么该子路经的非最短系数为2.49,远大于非最短系数的上限λ=1.7,所以,第2条路径不满足有效路径的判定条件。若调整非最短系数上限λ=2.5,那么第2条路径即可满足有效路径的判定条件。但是,由于绕道里程太长,在一般情况下旅客不会选择第2条路径出行,其实,设置λ=1.7是符合绝大多数旅客的出行路径习惯的。 表2 有效路径Table 2 Effective paths 图4 有效路径示意图Fig.4 Effective paths diagram 4.2.2 换乘方案分析 不同计划出发时间的旅客最优换乘方案选择情况如图5所示,将计划出发时间划分了7个时段,每个时段内的乘客具有相同的最优乘车方案。在时段①内计划出行的旅客需要换乘1次,这是因为该时段的旅客若要选择直达方案,将会等待很长时间,出行时间调整费用过高,因此宁愿选择换乘1次的方案出行;其他时段内列车发车频率较高,出行时间调整费用较小,因此旅客都愿意选择直达方案,和实际情况相符合。 图5 不同计划出发时间的最优换乘方案Fig.5 Optimal transfer scheme at different expected departure time 本文在分析铁路旅客出行路径特征的基础上,通过引入非最短系数概念,给出了有效路径的判定条件,设计了有效路径快速搜索算法。设计了前序弧数法,基于有效路径集快速搜索任意计划出发时间的旅客最优换乘方案。整体算法由2部分组成,一是整个铁路网络有效路径的预先生成和存储;二是给定计划出发时间和起讫站点的最优换乘方案的快速搜索。在不断变化的换乘网络中搜索当前最优换乘方案时,本文设计的算法实现了既考虑铁路旅客的出行路径特征又突出“快速搜索”的特点的目的。基于2014年中国高速铁路网络及运行图进行算例分析,算例结果显示全路网有效径路的生成和存储平均耗时50 s,任意一个最优换乘方案的搜索时间不足0.1 s,算法具有较高的运算效率和很强的实用性。 [1] 张铱莹,彭其渊. 综合运输旅客换乘网络优化模型[J]. 西南交通大学学报,2009,44(4):517-522. ZHANG Yiying, PENG Qiyuan. Optimization model of passenger transfer network for integrated transportation [J]. Journal of Southwest Jiaotong University,2009,44(4):517-522. [2] 崔炳谋,马钧培,陈光伟,等. 铁路旅客旅行换乘方案优选算法[J]. 中国铁道科学, 2007,28(6):122-127. CUI Bingmou, MA Junpei, CHEN Guangwei, et al. Optimal algorithm of travel transfer scheme for railway passengers [J]. China Railway Science,2007, 28(6):122-127. [3] 杨信丰,刘兰芬,李引珍,等. 多目标铁路旅客乘车方案优化模型及算法研究[J]. 交通运输系统工程与信息,2013,13(5):72-78. YANG Xinfeng, LIU Lanfen, LI YInzhen, et al. Route selection for railway passengers: A multi-objective model and optimization algorithm [J]. Journal of Transportation Systems Engineering and Information Technology,2013,13(5):72-78. [4] 林冬梅,刘军. 限制网络上的铁路旅程规划快速求解算法[J]. 铁道学报,2013,35(2):8-13. LIN Dongmei, LIU Jun. A fast algorithm for railway route planning on restricted network [J]. Journal of the China Railway Society,2013,35(2):8-13. [5] 史峰,邓连波. 旅客换乘网络优化设计[J]. 铁道科学与工程学报,2004,1(1):78-82. SHI Feng, DENG Lianbo. Optimal design of passenger transfer network [J]. Journal of Railway Science and Engineering,2004,1(1):78-82. [6] Hart P E, Nilsson N J, Raphael B. A formal basis for the heuristic determination of minimum cost paths in graphs [J]. IEEE Transactions of Systems Science and Cybernetics, 1968, 4(2):100-107. [7] 史峰,马钧培,向联慧,等. 客运中转径路的换乘模型及算法[J]. 铁道学报,1999,21(5):1-4. SHI Feng, MA Junpei, XIANG Lianhui, et al. A Transfer model and its algorithm of the transfer route in railway passenger transportation [J]. Journal of the China Railway Society, 1999,21(5):1-4. [8] 王华,季令. 我国铁路客运合理径路选择的研究[J].上海铁道大学学报,1999,20 (4):51-54. WANG Hua, JI Ling. Research an rational pathway assemble in our national railway[J]. Journal of Shanghai Tiedao University, 1999,20 (4):51-54. [9] 吕晓艳,刘春煌,单杏花,等. 基于车次径路约束下的客运径路生成算法优化[J]. 中国铁道科学,2007, 28(3):122-125. LÜ Xiaoyan, LIU Chunhuang, SHAN Xinghua, et al. Optimal on route computation algorithm based on train-route restriction [J]. China Railway Science,2007,28(3):122-125. [10] DOU Fei, YAN Kai, HUANG Yakun, et al. Optimal path choice in railway passenger travel network based on residual train capacity [J]. The Scientific World Journal, 2014:1-8. Fastsearch algorithm of transfer scheme based on effective paths in railway networks SU Huanyin1, SHI Feng1, ZHANG Pei2, WEI Tangjian1,3 (1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China;2. Zhengzhou Railway Department, Zhengzhou 450052, China;3.School of Rail Transit, East China Jiaotong University, Nanchang 330013, China) Research on fast search algorithm of transfer scheme for railway passengers can provide supports to ticket booking system. Through analyzing characters of rail passenger travel paths, this paper designs decision conditions of an effective path by non-shortest coefficient and develops a search algorithm for effective paths. Based on the set of effective paths, a fast search algorithm of transfer scheme with minimum cost at any expected departure time is proposed by a front-arc-number method. The whole algorithm in this paper includes two parts: firstly, producing and storing effective paths of the whole railway network in advance; secondly, searching a transfer scheme with minimum cost on effective paths with the given departure time and O-D pair. This algorithm captures passenger’s travel characters and lights the fast-search feature. Numerical experiment is conducted based on China high-speed railway network and train schedule in 2014, and results verify the effectiveness and utility of the algorithm. rail transit; transfer scheme; effective path; non-shortest coefficient; train schedule 2016-01-26 国家自然科学基金资助项目(U1334207);中南大学博士生自主探索创新项目(2015zzts046) 史峰(1956-),男,湖南芷江人,教授,博士,从事交通流理论,运输网络优化研究;E-mail:shifeng@csu.edu.cn U293.32 A 1672-7029(2016)12-2496-07



3 基于有效路径的换乘方案搜索算法









4 算例分析




5 结论

