损耗型单负材料双层异质结构的反常场局域

董丽娟， 石泰侠， 邓富胜， 刘丽想， 石云龙， 刘艳红*

(1. 山西大同大学 微结构电磁功能材料省市共建山西省重点实验室， 山西 大同 037009；2. 太原理工大学 材料科学与工程学院， 山西 太原 030024)



损耗型单负材料双层异质结构的反常场局域

董丽娟1， 石泰侠2， 邓富胜1， 刘丽想1， 石云龙1， 刘艳红1*

(1. 山西大同大学 微结构电磁功能材料省市共建山西省重点实验室， 山西 大同 037009；2. 太原理工大学 材料科学与工程学院， 山西 太原 030024)

通过计算损耗型单负材料双层异质结构中的透射、反射和吸收随损耗系数的变化，对单负材料双层异质结构基于损耗的光学性质调控进行了研究。首先，对损耗型单负材料单层结构的透射行为进行了计算，给出了单层结构随损耗系数增大的非单调透射的变化图像。接着，计算了损耗型单负材料双层异质结构中的透射、反射和吸收随损耗系数的变化曲线，并分析了不同频率下透射与损耗系数之间的关系。研究结果表明，在远离隧穿频率处，随损耗系数的逐渐增大，异质结的透射呈现出先减小后增大的变化。计算的电磁场强度分布图像表明，双层异质结中透射与损耗系数之间为非单调关系，起源于损耗型单负材料界面处的反常场局域效应，即随着损耗系数的增大，场局域先减弱后增强。

单负材料； 光学性质； 异质结构

1 引 言

特异材料是指由亚波长微结构单元组成的人工电磁材料，其等效介电常数和磁导率可以通过微结构设计进行任意调控。随着特异材料(Metamaterials)的研究发展[1]，对实验制备人工微结构材料的要求越来越高。单负材料(Single-negative materials)是特异材料的一种，按仅介电常数小于0，或者仅磁导率小于0，可分为负介电常数材料和负磁导率材料。两种单负材料是组成双负材料(Double-negative materials)的基本结构，既实现了单负材料的实验制备，又可以利用它们构造双负材料。同时，单负材料复合结构中的许多新奇的物理性质[2-3]，可以用来设计新型的光学器件。但是，目前对于特异材料的人工制备，多数原料来源于金属，即利用金属微结构的设计实现对等效材料介电常数和磁导率的调控[4-6]。众所周知，损耗是金属材料中不可避免的因素，它严重地限制了金属材料的利用，同时很大程度上局限了特异材料广泛的应用范围。因此，损耗的问题是特异材料发展中急需解决的实际问题[7-12]。

损耗型单负材料，在等离子体频率以下范围可以看作金属材料。由于损耗型单负材料的折射率是复数且实部不能大于虚部，导致该材料的光学性质与其他材料不同。通过分析透射、反射和吸收随损耗系数的变化，我们研究了损耗型单负材料单层结构中反常的非单调透射变化规律[13-16]。本文在该研究成果的基础上，研究了损耗型单负材料双层异质结构中的反常电磁场局域现象。单负材料双层异质结构的性质与单层结构完全不同，它们的电磁场会局域在负介电常数材料和负磁导率材料的界面上[2]。结果证明，在损耗型单负材料双层异质结构中，隧穿频率处于其他频率处的透射随损耗系数的变化不同。在隧穿频率处，由于两种单负材料的匹配原因，导致透射率会随损耗系数增大一直降低；在远离隧穿频率的低频处，透射率依然会随损耗系数增大呈现非单调的变化。

2 损耗型单负材料的反常透射原理

考虑一个由空气层和半无限介质层组成的双层结构，折射率分别为1和n。由菲涅尔公式可以给出空气层和介质层之间界面上的反射率公式：

(1)

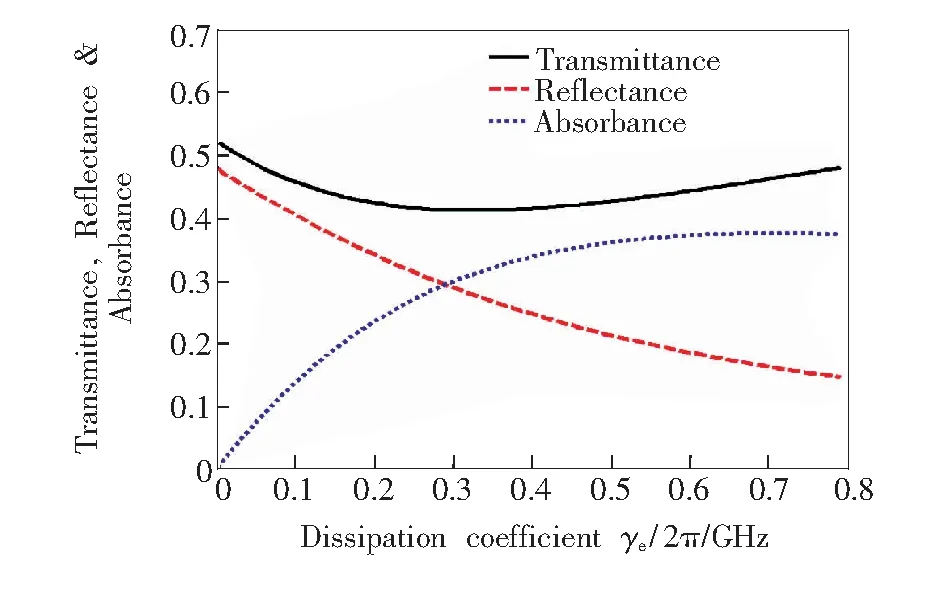
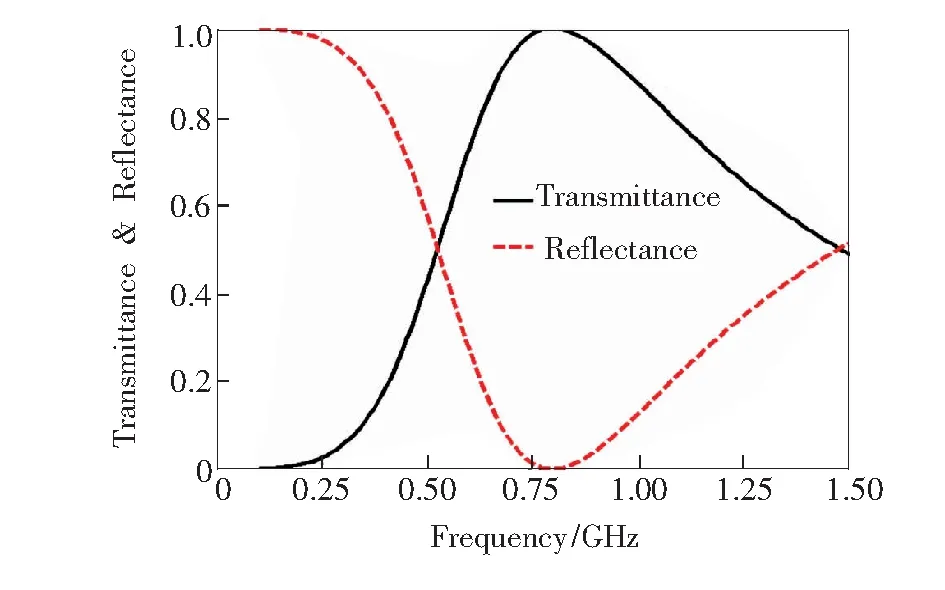
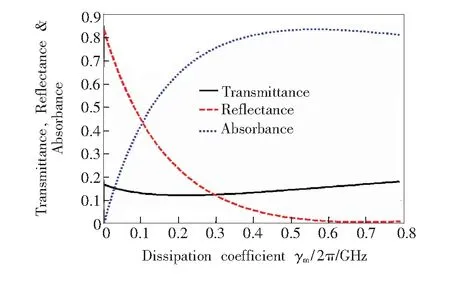
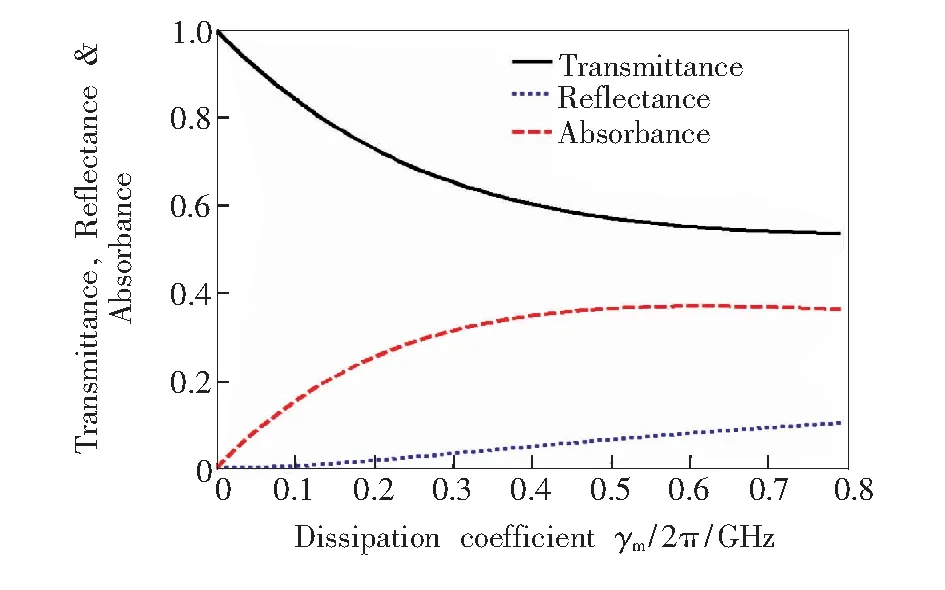
其中n1和n2分别代表介质层折射率n的实部和虚部。下面分析两种变化趋势：一是半无限介质层是介电材料(n1>n2)时，双层结构的反射率R随n2的变化趋势；第二种是半无限介质层是损耗型单负材料(n1

(2)

其中n21和n22分别表示两种不同介电材料的折射率虚部。从式(2)可以看到，当n22>n21时，R2>R1。这个结果表明，如果介电材料的损耗越大(也就是说，n2越大)，将有更多的电磁波被反射。由此可知，对于空气和半无限介质双层结构，随着介电材料损耗的增大，反射率和吸收率都将增大，导致结构的透射率降低。然而，对于空气层和单负材料层组成的双层结构，假设单负材料是理想材料，从式(1)可以推导反射率R=1(n1为0)。假设单负材料是实际材料，则损耗(n1不为0)不可避免。为了简单起见，假设n2不变，则随着n1的增大(即损耗增大)，根据式(1)，反射率R将会单调减小，这个结果将导致更多的电磁波进入双层结构。因此，对于损耗型单负材料，如果反射率的减小幅度比结构吸收率的增大幅度小，将会导致透射率降低；如果前者比后者的幅度大，将会导致透射率提高，变化量将依赖于反射率和吸收率之间变化幅度的竞争强弱。

3 损耗型单负材料的反常透射

3.1 单层结构

负介电常数材料和负磁导率材料是两种不同的单负材料，前者介电常数小于0，磁导率大于0；后者磁导率小于0，介电常数大于0。负介电常数材料的介电常数和磁导率分别为：

(3)

负磁导率材料的介电常数和磁导率分别为：

(4)

其中ωep和ωmp分别为电等离子体频率和磁等离子体频率，γe和γm分别为负介电常数材料和负磁导率材料的损耗系数。本文只考虑(从负介电常数材料一侧)垂直入射情况。

考虑一个置于空气中的负介电常数材料单层结构，厚度为15 mm，ωep为10 GHz，μ1为3。图1给出了0.6 GHz处该单层结构的透射率、反射率和吸收率随损耗系数γe/2π的变化曲线。从图中可以看到，透射率随损耗系数的变化呈现先降低后提高的反常非单调变化趋势。也就是说，损耗增大到一定程度时，透射率反而出现了提高的现象。透射率的提高是由于反射率随损耗系数的增大而一直降低。图1中的反射率一直呈降低趋势，更多的电磁波能量进入了该结构，虽然吸收率同时也在提高，但是如果吸收率提高的幅度没有反射率降低的幅度大，那么透射率也就提高了。因此，透射率提高的多少在于反射率与吸收率变化量之间的竞争关系。同理，由于负磁导率材料与负介电常数材料参数的对称性，它也具有同样的性质。由此可见，透射率随损耗系数的反常变化是单负材料特有的一种性质。

图1 单层损耗型负介电常数材料透射率、反射率和吸收率随损耗系数的变化(0.6 GHz)。

Fig.1 Transmittance, reflectance and absorbancevs. dissipation coefficient in single layer lossy epsilon-negative materials (0.6 GHz).

3.2 双层结构

考虑一个置于空气中的负介电常数材料和负磁导率材料组成的双层异质结构，电磁波从左侧入射，即负介电常数材料层入射。两种材料的厚度都为15 mm，ωep和ωmp都为10 GHz，μ1和ε2都为3。当不考虑负介电常数材料和负磁导率材料损耗时，根据虚阻抗和虚相位匹配，可以得到该共轭结构的隧穿谱，如图2所示。可以看到，透射率在0.8 GHz处达到了隧穿，反射率为0。当考虑负磁导率材料损耗时，取γe=0，计算双层异质结构的透射率、反射率和吸收率随损耗系数γm/2π的变化，如图3所示。图3中给出的是对应于图2中频率为0.4 GHz时的透射率、反射率和吸收率随损耗系数的变化情况。可以看到，透射率随损耗系数的增大呈现先降低后提高的反常非单调变化趋势。其原因与单层单负材料结果一样，在损耗系数增大的过程中，反射率单调下降，吸收率先急速提高后缓慢下降，最终导致透射率先降低后提高的结果。然而，我们发现，并不是在双层异质结构所有对应的频谱中都会出现反常的透射现象，如图4所示。图4给出了双层异质结构中隧穿频率0.8 GHz处对应的透射率、反射率和吸收率随损耗系数增大的变化情况。可以看到，透射率随损耗系数的增大一直处于降低的状态，而反射率一直在提高，即使吸收率在损耗系数很大处变化平缓，也会由于反射率的提高而导致透射率降低。这是因为反射率的持续提高会导致越来越少的电磁波能量进入结构中。那么，为什么在0.4 GHz处可以出现反常的透射现象，却在隧穿频率0.8 GHz处没有出现呢？原因在于单负材料的双层异质结构具有特殊的隧穿效应，损耗系数的增大导致虚相位和虚阻抗匹配的条件越来越不满足，所以透射率一定是单调递减的。因此，在隧穿频率附近，透射率随损耗系数的变化都是单调递减的变化过程；而在远离隧穿频率处，透射率随损耗系数的变化才可以出现反常的非单调透射变化过程。

图2 双层异质结构无损耗时透射率和反射率随频率的变化

Fig.2 Transmittance and reflectancevs. frequency in double layers heterostructure with lossless

图3 双层异质结构透射率、反射率和吸收率随损耗系数的变化(0.4 GHz)。

Fig.3 Transmittance, reflectance and absorbancevs. dissipation coefficient in double layers heterostructure (0.4 GHz).

图4 双层异质结构透射率、反射率和吸收率随损耗系数的变化(0.8 GHz)。

Fig.4 Transmittance, reflectance and absorbancevs. dissipation coefficient in double layers heterostructure (0.8 GHz).

4 反常的电磁场局域现象

在由负介电常数材料和负磁导率材料组成的双层异质结构中，电磁波入射该结构时，由于需要满足麦克斯韦边界条件，会在负介电常数材料和负磁导率材料的界面上形成局域模。界面模局域的强弱决定了电磁波透射的高低程度。因此，若要解释在0.4 GHz频率处的电磁波透射存在反常的非单调透射的物理原因，需要先计算在该频率处界面模的局域情况。图5给出了0.4 GHz频率处的双层异质结构中，在不同损耗系数时的电磁场强度随材料厚度的分布情况。以电场强度分布为例，图中黑色、蓝色和绿色实线分别是损耗系数为0.000 01，0.1，0.6 GHz时的电场强度分布。可以看到，随损耗系数的增大，电场强度的局域程度先减弱后增强。

图5 不同损耗系数下，0.4 GHz时的电磁场强度分布图。

Fig.5 Distribution of electromagnetic field intensity with different dissipation coefficient at 0.4 GHz

从图5可以看到，磁场强度的分布变化情况也是如此。这样的结果正好解释了在该频率处透射率随损耗系数的增大具有反常的非单调变化趋势。

5 结 论

利用转移矩阵方法，根据单负材料特有的反常非单调透射现象，研究了单负材料双层异质结构中的反常透射和场局域现象。对于双层异质结构，分别讨论了远离隧穿频率处和隧穿频率处的透射率、反射率和吸收率随损耗系数增大时的变化趋势。在远离隧穿频率处，双层异质结构呈现透射率随损耗系数增大的反常非单调变化趋势，并且给出了该频率处的电磁场强度分布曲线。正是由于电磁场强度随损耗系数增大呈现先减弱后增强的变化趋势，才导致了该频率处的反常透射。在隧穿频率处，由于损耗系数增大对隧穿条件减弱的影响，导致该频率处的透射随损耗系数不会出现反常现象。

[1] OLIVERI G, WERNER D H, MASSA A. Reconfigurable electromagnetics through metamaterials—a review [J].Proc.IEEE, 2015, 103(7):1034-1056.

[3] JIANG H T, CHEN H, LI H Q,etal.. Properties of one-dimensional photonic crystals containing single-negative materials [J].Phys.Rev. E, 2004, 69(6):066607.

[4] SHEN B, POLSON R, MENON R. Metamaterial-waveguide bends with effective bend radius < λ0/2[J].Opt.Lett., 2015, 40(24):5750-5753.

[5] BHASKAR M, JOHARI E, AKHTER Z,etal.. Gain enhancement of the vivaldi antenna with band notch characteristics using zero-index metamaterial [J].MicrowaveOpt.Technol.Lett., 2016, 58(1):233-238.

[6] WU H W, WANG F, DONG Y Q. Cavity modes with optical orbital angular momentum in a metamaterial ring based on transformation optics [J].Opt.Express, 2015, 23(25):32087-32097.

[7] JIANG Z H, YUN S, LIN L,etal.. Tailoring dispersion for broadband low-loss optical metamaterials using deep-subwavelength inclusions [J].Sci.Rep., 2013, 3:1571.

[8] YUN S, JIANG Z H, XU Q,etal.. Low-loss impedance-matched optical metamaterials with zero-phase delay [J].Acs.Nano, 2012, 6(5):4475-4482.

[9] SUN L, YU K W. Strategy for designing broadband epsilon-near-zero metamaterial with loss compensation by gain media [J].Appl.Phys.Lett., 2012, 100:261903.

[10] SUN L, FENG S, YANG X D. Loss enhanced transmission and collimation in anisotropic epsilon-near-zero metamaterials [J].Appl.Phys.Lett., 2012, 101(24):241101.

[11] RODRIGO S G, GARCIA-VIDAL F J, MARTIN-MORENO L. Theory of absorption-induced transparency [J].Phys.Rev. B, 2013, 88(15):155126.

[12] FENG S. Loss-induced omnidirectional bending to the normal in-near-zero metamaterials [J].Phys.Rev.Lett., 2012, 108(19):193904.

[13] DONG L J, DU G Q, JIANG H T,etal.. Transmission properties of lossy single-negative materials [J].J.Opt.Soc.Am. B, 2009, 26(5):1091-1096.

[14] LIU Y H, JIANG H T, CHEN H. Experimental investigation on transmission properties of lossy single-negative metamaterials [J].Eur.Phys.J. B, 2012, 85:11-16.

[15] LIN W H, WU C J, CHANG S J. Angular dependence of wave reflection in a lossy single-negative bilayer [J].Prog.Electromag.Res., 2010, 107:253-267.

[16] LIN W H, WU C J, CHANG S J. Analysis of angle-dependent unusual transmission in lossy single-negative (SNG) materials [J].SolidStateCommun., 2010, 150:1729-1732.

董丽娟(1976-)，女，山西襄汾人，博士，副教授，2009年于同济大学获得博士学位，主要从事人工微结构材料的研究。

E-mail: donglijuan_2012@163.com

刘艳红(1979-)，女，山西文水人，博士，副教授，2013年于同济大学获得博士学位，主要从事人工微结构材料的研究。

E-mail: lyh030114@163.com

Abnormal Localized Field in Double Layers Heterostructure with Lossy Single-negative Materials

DONG Li-juan1, SHI Tai-xia2, DENG Fu-sheng1, LIU Li-xiang1, SHI Yun-long1, LIU Yan-hong1*

(1.ShanxiProvincialKeyLaboratoryofElectromagneticFunctionalMaterialsforMicrostructure,ShanxiDatongUniversity,Datong037009,China;2.SchoolofMaterialsScienceandEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China)

The effects of material loss on light propagation in heterostructure comprising of two single-negative layers were studied, with the aim of light manipulation based on loss. Firstly, transmission of a single-negative layer was calculated, and the variation of the non-monotonic transmission with the dissipation coefficient in the structure was given. Then, the relationships of the transmission, reflection and absorption with the dissipation coefficient in the double layer heterostructure of the two single-negative materials were dicussed, and the variation of the transmission at different frequency was analyzed. Finally, the distribution of the electromagnetic field intensity was shown in order to explain the anomalous transmission phenomenon with the dissipation coefficient. The results illuminate that the anomalous nonmonotonic transmission behavior with the increasing of dissipation coefficient remains in the double layer heterostructure of the single-negative materials, only at the far from tunneling frequencies. This reason is the anomalous localized fields in the interface between two different single-negative materials.

single-negative materials; optical property; heterosturcture

2016-04-23；

2016-05-26

国家自然科学基金(11274207，11504210，11504211)； 山西省攻关计划(2015031002-2)； 大同市攻关计划(2015015，201308，201422-3)资助项目

1000-7032(2016)07-0887-05

O469

A

10.3788/fgxb20163707.0887

*CorrespondingAuthor,E-mail:lyh030114@163.com