利用陷光结构增加硅薄膜太阳能电池的吸收效率

沈宏君， 李 婷， 卢辉东， 黄仙健， 李新兰

(1. 宁夏大学 物理电气信息学院， 宁夏 银川 750021； 2. 青海大学 新能源光伏产业研究中心， 青海 西宁 810016)



利用陷光结构增加硅薄膜太阳能电池的吸收效率

沈宏君1*， 李 婷1， 卢辉东2， 黄仙健1， 李新兰1

(1. 宁夏大学 物理电气信息学院， 宁夏 银川 750021； 2. 青海大学 新能源光伏产业研究中心， 青海 西宁 810016)

提出了一种含有光锥光子晶体防反射层和四棱锥光栅背反射层的a-Si薄膜太阳能电池结构，吸收层厚1 μm，总厚度为1.45 μm。根据光子晶体及亚波长光栅的衍射特性，利用严格耦合波方法对器件参数进行了优化。计算结果表明：当光锥结构倾角θ=72°、晶格常数T1=1 200 nm、介质底半径r=100 nm时，防反射层的透射率较高，在300～600 nm波长范围内，该薄膜太阳能电池的吸收效率比不含防反射层电池提高了11.54%；当四棱锥光栅结构周期L=1.2 μm、占空比f=0.38、槽深h5=560 nm时，背反射层的反射效果较好，在600～850 nm波长范围内，电池的吸收效率提高了3.75%。所设计的薄膜电池结构在波长为300～750 nm、入射角为0°～75°范围内的吸收效率均在80%以上，平均吸收效率达92%，满足太阳电池对宽频谱、广角度的光俘获的要求。

薄膜太阳能电池； 光子晶体； 亚波长光栅； 严格耦合波； 衍射效率

1 引 言

近年来，光伏太阳能电池没能实现大规模商业化生产，其主要限制性因素是较低的光电转化效率和较高的制作成本。到目前为止，Si太阳能电池所能达到的最高效率仅为(25.6±0.5)%[1]。在一般的硅(Si)太阳能电池中，Si材料的使用成本占整个结构制作成本的40%[2]。20世纪80年代末，Green等[3]提出了薄膜太阳能电池结构(0.2～50 μm)，有效减少了半导体材料的使用量。然而薄膜太阳能电池对光的吸收率相对较低，因此有效陷光机制的运用是非常必要的。

亚波长光栅具有减反射和偏振双折射效应，且二维亚波长光栅的偏振敏感性较低，因此，不同面型的二维亚波长光栅一经提出便被广泛应用在薄膜太阳能电池中。Li等[4]提出了二次面型防反射光栅并证明其具有较好的防反射特性。 Lin提出一种背反射层和闪耀光栅结合的薄膜太阳能电池结构，可使衍射效率加倍[5]。亚波长光栅能有效增加光的传播路径，因此通常用亚波长光栅作背反射层以增加太阳能电池的光俘获。 Biswas等[6]证明，具有粗糙化背反射层的太阳能电池结构的最优吸收率可超过传统的朗伯限制(4n2)。Li等[7]设计了防反射层为光栅结构、背反射层为金属光栅的非晶硅薄膜太阳能电池，在0.3～0.6 μm、0.6～0.84 μm的入射光波长范围内，吸收效率分别提高了0.4%～10.8%和20%～385%。1987年，Yablonovich[8-9]提出光子晶体的概念，因其特殊的对光子的控制能力，且存在完全带隙可以完全反射带隙内频段的光波，进而成为薄膜太阳能电池中防反射层[10]或背反射层[11]结构的最佳选择。在不使用其他材料作为防反射层的前提下，Domínguez 等[10]利用1D光子晶体使得防反射层在500～900 nm波长范围内的平均反射率低于10%。Yu等[11]证明用1D光子晶体作分布布拉格反射器可以有效改善基于P3HT∶ICBA混合物的半透明聚合物太阳能电池的性能，600 nm时的最高传输效率达到了80.4%。Chutinan等[12]将2D光子晶体作为活性区域，证明2 μm厚的c-Si太阳能电池的效率可提高11.15%。金属表面等离子体可以将电磁场集中在纳米尺度范围内，使场强得到大幅度的提高[13-14]。武振华等[15]通过计算得出，具有Ag/ZnO背反射器的电池结构的短路电流密度与不含背反射器的电池结构相比提高了3.19 mA/cm2。

本文根据光栅、光子晶体及金属的光学特性，设计了一种光子晶体结构作为防反射层、亚波长光栅结构作为背反射层的非晶硅(a-Si)薄膜太阳能电池结构。文中运用严格耦合波方法(RCWA)[16-17]分析a-Si薄膜太阳能电池，优化结构参数，使其实现了宽频谱、广角度的较高吸收。

2 结构模型

严格耦合波方法是用于分析亚波长周期结构的矢量衍射理论，通过严格求解Maxwell方程组，结合边界条件可以得到衍射效率。该方法的精确性取决于计算过程中所保留的衍射级次，且具有良好的收敛性。该方法最初用于研究一维光栅的衍射效率，现在已经广泛应用于计算不同面型不同周期的光栅结构[18]。

本文设计的薄膜太阳能电池结构模型如图1所示，从上至下依次为防反射层、折射率渐变介质层、活性层、背反射层。其中防反射层是介质柱为光锥结构的光子晶体，以SiO2为基底填充Si3N4；折射率渐变介质层分别为ITO和TiO2，可有效减少入射光的反射；活性层即为光的吸收层，本文材料为a-Si；背反射层由ZnO四棱锥亚波长光栅及Ag基底组成。

图1 薄膜太阳能电池结构模型图

Fig.1 Schematic illustration of the investigated thin-film solar cell

其中Si3N4的折射率为2，ITO折射率为1.9，SiO2折射率满足cauchy模型[19]：

(1)

其中A=1.491，B=0.006 86，C=-0.000 764 8。

TiO2折射率满足公式[20]：

(2)

ZnO折射率满足公式[21]：

图2 Ag(a)和a-Si(b)的折射率、消光系数曲线。

Fig.2 Refractive indexnand extinction coefficientkof Ag (a) and a-Si (b)

Ag和a-Si的折射率n、消光系数k随波长的变化如图2所示[22]。

3 结果与讨论

以横磁波(TM极化波)为例，我们对入射波长为500 nm、入射角为0°、h2=h3=60 nm时的防反射层光锥光子晶体进行优化，其中入射区介质为空气，出射区介质为a-Si。本结构的衍射效率与光锥倾角θ、介质层厚度h1、介质底半径r及晶格常数T1有关。

分别对光锥光子晶体的光锥参数进行优化，结果如图3所示。其中图3(a)为透射率随倾角θ的变化曲线，可以看出透射率随倾角θ呈周期性变化。当θ=3°，25°，47°，72°时，透射率变化范围较小，具有良好的冗余度。对于光锥结构而言，倾角越大越容易实现光沿Z轴方向的传输，因此，我们取倾角θ=72°。透射率随介质柱高度h1，即槽深变化的曲线如图3(b)所示。当h1=720 nm时，透射率最高达99.36%。晶格常数T1分别为200，600，900，1 200，1 600 nm时，透射率随介质底半径r的变化曲线如图3(c)所示。从制作工艺方面考虑，我们令晶格常数T1=1 200 nm、介质底半径r=100 nm。图3(d)是防反射层在全波段及全角入射情况下的透射率分布，红色表示透射率高；蓝色则表示透射率低。可以看出入射角在0°～80°的全波段均有高透射，最高达99.99%，平均透射率为94.74%；全角全波段的平均透射率为90.63%，具有较好的防反射效果。

图3 (a)防反射层透射率随光锥倾角的变化；(b)防反射层透射率随光锥高度的变化；(c)不同光锥光子晶体周期下的透射率随光锥底半径的变化；(d)防反射层透射率分布。

Fig.3 (a) Transmittance of AR coating layervs. light cone angles. (b) Transmittance of AR coating layervs. light cone height. (c) Transmittance of AR coating layervs. light cone bottom radius for different photonic crystal periods. (d) Distribution of the transmittance of the AR coating layer.

入射光在防反射层的作用下会产生相移[23]：

(4)

其中n为光子晶体介质柱折射率的实部，h为槽深，λ为入射光波长。当相移为π的奇数倍时，仅传输奇数级衍射级次，如级次m=±1，±3，…；而当相移为π的偶数倍时，仅传输偶数级衍射级次，如级次m=0，±2，±4，…。其中大部分光强集中在0级，且相移φ随波长变化，因此图3(d)中出现了透射率随波长交替增大或减小的情况。

由图2(a)可知Ag的折射率较低，更容易发生全反射，而消光系数高则使得介质容易吸收到达Ag介质表面的光波而增加损耗[7]。ZnO具有较强的抵抗氢等离子体的特性，为了减少金属损耗，在a-Si层和金属层之间插入ZnO层[7,24]。反射光栅的衍射可有效增加活性层中的有效光程。本文设计的背反射层结构即在活性层a-Si与金属Ag之间插入ZnO四棱锥光栅结构，其中Ag的厚度为50 nm。

在特定波长范围内，太阳能电池的光吸收能力强烈依赖于光栅的占空比(f=S1/S2,其中S1为介质柱底面积，S2为光栅单位周期的面积)和槽深[25]。在四棱锥光栅结构周期L=1.2 μm条件下，我们对该结构进行了优化计算。其中入射区域为a-Si吸收层，透射区域为空气。计算结果如图4所示：其中图4(a)表示波长分别为500，700，850 nm时，背反射层结构的反射率随占空比f的变化，根据计算结果取f=0.38；图4(b)表示波长分别为500，700，850 nm时，背反射层结构的反射率随槽深h5的变化，根据计算结果取h5=560 nm；图4(c)表示波长分别为300，500，700，850 nm时，背反射层结构的反射率随入射角的变化。由于ZnO介质与a-Si的折射率差较大导致容易发生全反射及光程的增加，在入射角大于28°时，该背反射结构对全波段入射光的反射率均可达到98%以上。

图4 (a)反射率随光栅占空比的变化；(b)反射率随光栅槽深的变化；(c)反射率随入射角的变化。

Fig.4 (a) Reflectancevs. grating duty cycle. (b) Reflectancevs. grating height. (c) Reflectancevs. incident angle.

4 计算比较

优化后的电池结构总厚度为1.45 μm，其中吸收层厚1 μm，其随波长及入射角变化的吸收效率如图5所示。纵坐标表示入射角的大小，取值范围在0°～89°之间，红色区域对应吸收率较高的波段及入射角范围。从图中可以看出，波长为300～750 nm、入射角为0°～75°时，该薄膜太阳能电池的吸收效率几乎均在80%以上，平均吸收效率为92%。由图2(b)可知，a-Si在700～850 nm之间的消光系数趋近于0，因此对长波段区域的吸收效率相对较低。

与不具有光锥光子晶体防反射层的电池结构和同时不含光锥光子晶体防反射层、四棱锥光栅背反射层的电池结构相比较，该电池结构吸收效率均有较大提高。入射角为50°时，电池吸收效率随波长变化曲线如图6所示。数值结果如表1所示。从表中可知，光锥光子晶体防反射层主要在300～600 nm波段起作用，使得薄膜太阳能电池的吸收效率提高11.54%；而四棱锥光栅背反射层主要在600～850 nm波段具有增强吸收的作用，吸收效率提高了3.75%。

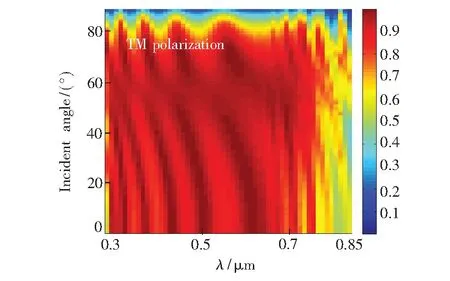
图5 太阳能电池的吸收效率分布

图6 防反射层及背反射层对太阳能电池吸收效率的影响

Fig.6 Effect of AR coating and the presence of the reflector on the absorption spectrum of the solar cell

表1 3种薄膜太阳能电池在不同波段下的吸收率

Tab.1 Absorption efficiencies of the three devices within different wave band

电池300～600nm600～850nm无陷光结构83．28%74．44%无防反射层83．28%78．19%有陷光结构94．82%78．62%

入射角分别为10°和70°时，本文设计的薄膜太阳能电池结构及无陷光结构薄膜太阳能电池的吸收效率随波长的变化如图7(a)、(b)所示。

结合图6、图7及表1、表2可知，本文所设计的薄膜太阳能电池结构在300～600 nm波长范围的光吸收能力明显增强。以10°和70°入射时，有陷光结构的薄膜太阳能电池比无陷光结构的薄膜太阳能电池的平均吸收率分别增加了13.5%和8%；在波长为600～850 nm区域，吸收效率分别提高了4.5%和3.5%。可见，文所设计的薄膜太阳能电池结构成功地实现了在300～850 nm波长范围、广角度范围的吸收增强，具有实际应用的潜力。

图7 10°(a)和 70°(b)入射角度下，陷光结构对太阳能电池吸收效率的影响。

Fig.7 Effect of light traping structure on the absorption efficiency of the solar cell with the incident angle of 10° (a) and 70° (b)

表2 两种薄膜太阳能电池在不同波段、不同入射角下的吸收率

Tab.2 Absorption of the two devices under illumination from light with different lambda and incident angle

电池300～600nm600～850nm10°70°10°70°有陷光结构90．5%92%78%81．5%无陷光结构77%84%73．5%78%

5 结 论

设计了含有光锥光子晶体防反射层和四棱锥光栅背反射层的a-Si薄膜太阳能电池结构，利用RCWA方法优化计算得出：当光锥结构倾角θ=72°、晶格常数T1=1 200 nm、介质底半径r=100 nm时，防反射层透射效率较高，且该结构使得该薄膜太阳能电池在300～600 nm波长范围内的平均吸收效率提高了11.54%；当四棱锥光栅结构周期L=1.2 μm、占空比f=0.38、槽深h5=560 nm时，背反射层的反射效果较好，电池在600～850 nm波长范围内的平均吸收效率提高了3.75%。并且该薄膜电池结构在波长为300～750 nm、入射角为0°～75°时吸收效率均在80%以上，平均吸收效率达92%。与不含陷光结构的薄膜太阳能电池相比，本文设计的太阳能电池结构在可见光波长范围、广角度内均实现了光吸收的增强，增加了光伏太阳能电池商业化生产的可能性。

[1] GREEN M A, EMERY K, HISHIKAWA Y,etal.. Solar cell efficiency tables (version 46) [J].Prog.Photovolt.:Res.Appl., 2015, 23(7):805-812.

[2] MUNZER K A, HOLDERMANN K T, SCHLOSSER R E,etal..Thin monocrystalline silicon solar cells [J].IEEETrans.ElectronDev., 1999, 46(10):2055-2061.

[3] GREEN M.ThirdGenerationPhotovoltaics:AdvancedSolarEnergyConversion[M]. Berlin Heidelberg: Springer-Verlag, 2003.

[4] LI X W, TAN Q F, JIN G F. Surface profile optimization of antireflection gratings for solar cells [J].Optik-Int.J.LightElectronOpt., 2011, 122(23):2078-2082.

[5] LIN L J H, CHIOU Y P. Improving thin-film crystalline silicon solar cell efficiency with back surface field layer and blaze diffractive grating [J].SolarEnergy, 2012, 86(5):1485-1490.

[6] BISWAS R, XU C. Photonic and plasmonic crystal based enhancement of solar cells—Theory of overcoming the Lambertian limit [J].J.Non-Cryst.Solids, 2012, 358(17):2289-2294.

[7] LI H H, WANG Q K, CHEN J,etal.. Light trapping in amorphous silicon solar cells with periodic grating structures [J].Opt.Commun., 2012, 285(5):808-815.

[8] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics [J].Phys.Rev.Lett., 1987, 58(20):2059-2062.

[9] YABLONOVITCH E. Photonic crystals [J].J.Mod.Opt., 1994, 41(2):173-194.

[10] DOMíNGUEZ S, GARCíA O, EZQUER M,etal.. Optimization of 1D photonic crystals to minimize the reflectance of silicon solar cells [J].Photon.Nanostruct.-Fundam.Appl., 2012, 10(1):46-53.

[11] YU W J, SHEN L, LONG Y B,etal.. Highly efficient and high transmittance semitransparent polymer solar cells with one-dimensional photonic crystals as distributed Bragg reflectors [J].Org.Electron., 2014, 15(2):470-477.

[12] CHUTINAN A, KHERANI N P, ZUKOTYNSKI S. High-efficiency photonic crystal solar cell architecture [J].Opt.Express, 2009, 17(11):8871-8878.

[13] 时彦朋,王晓东,刘雯,等. 新型硅薄膜太阳能电池混合陷光结构 [J]. 光子学报, 2014, 43(5):0523001-1-5. SHI Y P, WANG X D, LIU W,etal.. New hybrid light trapping structure in silicon thin film solar cells [J].ActaPhoton.Sinica, 2014, 43(5): 0523001-1-5. (in Chinese)

[14] PATTNAIK S, CHAKRAVARTY N, BISWAS R,etal.. Nano-photonic and nano-plasmonic enhancements in thin film silicon solar cells [J].SolarEnergyMater.SolarCells, 2014, 129:115-123.

[15] 武振华,李思敏,张文涛,等. 一维和双层二维光子晶体太阳能电池背反射器 [J]. 光子学报, 2016, 45(2):0223003-1-5. WU Z H, LI S M, ZHANG W T,etal.. Back reflector of solar cells consisting of one-dimensional photonic crystal and double-layered two-dimensional photonic crystal [J].ActaPhoton.Sinica, 2016, 45(2):0223003-1-5. (in Chinese)

[16] MOHARAM M G, POMMET D A, GRANN E B,etal.. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: enhanced transmittance matrix approach [J].J.Opt.Soc.Am. A, 1995, 12(5):1077-1086.

[17] MOHARAM M G, GRANN E B, POMMET D A,etal.. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings [J].J.Opt.Soc.Am. A, 1995, 12(5):1068-1076.

[18] JIANG J H, DEGUZMAN P C, NORDIN G P. Analysis of stacked rotated gratings [J].Appl.Opt., 2007, 46(8):1177-1183.

[19] PHILIPP H R. Optical properties of silicon nitride [J].J.Electrochem.Soc., 1973, 120(2):295-300.

[20] DEVORE J R. Refractive indices of rutile and sphalerite [J].J.Opt.Soc.Am., 1951, 41(6):416-419.

[21] BOND W L. Measurement of the refractive indices of several crystals [J].J.Appl.Phys., 1965, 36(5):1674-1677.

[22] PALIK E D, GHOSH G.ElectronicHandbookofOpticalConstantsofSolids[M]. San Diego: Academic Press, 1999.

[23] ZHENG G G, XU L H, PEI S X,etal.. Theoretical analysis of performance improvement of thin film solar cells with two-dimensional photonic crystals and distributed Bragg reflector textured structures [J].Opt.Commun., 2013, 309:318-322.

[24] MüLLER J, RECH B, SPRINGER J,etal.. TCO and light trapping in silicon thin film solar cells [J].SolarEnergy, 2004, 77(6):917-930.

[25] SOLNTSEV S, ZEMAN M. Optical modeling of thin-film silicon solar cells with submicron periodic gratings and nonconformal layers [J].EnergyProced., 2011, 10:308-312.

沈宏君(1970-)，男，河南商丘人，博士，副教授，2009于北京邮电大学获得博士学位，主要从事光子晶体方面的研究。

E-mail: shenhongj2004@126.com

Enhancement of Light Absorption in Thin Film Silicon Solar Cells with Light Traping

SHEN Hong-jun1*, LI Ting1, LU Hui-dong2, HUANG Xian-jian1, LI Xin-lan1

(1.SchoolofPhysicsandElectricalInformation,NingxiaUniversity,Yinchuan750021,China;2.NewEnergyIndustryResearchCenter,QinghaiUniversity,Xining810016,China)

An amorphous silicon thin-film solar cell with an anti-reflection coating of light cone photonic crystal and a back surface field layer of rectangular pyramid grating is proposed. The thickness of the cell is 1.45 μm and the thickness of the absorbing layer is 1 μm. Using Rigorous Coupled Wave Analysis method, the parameters of the cell are optimized based the diffraction characteristics of the photonic crystal and the sub-wavelength grating. When the light cone angle is 72°, the lattice constant is 1 200 nm, and the bottom radius is 100 nm, a relative increase of 11.54% for the integrated absorption inside the solar cell can be achieved between 300 nm and 600 nm, compared to an equivalent but no anti-reflection coating cell. When the rectangular pyramid grating period is 1.2 μm, the duty cycle is 0.38, and the depth of the grating is 560 nm, a relative increase of 3.75% for the integrated absorption inside the solar cell can be achieved between 600 nm and 850 nm. According to the simulation, the absorption of the designed thin-film solar cell is over than 80% in the incident angle range of 0°-75° and the wavelength between 300 nm and 750 nm, and the average absorption is up to 92%. This solar cell is designed to meet the demanding requirements of a wide spectrum and wide-angle light capture.

thin-film solar cell; photonic crystal; sub-wavelength grating; rigorous coupled wave analysis; diffraction efficiency

2016-02-29；

2016-04-01

国家自然科学基金(61167002)资助项目

1000-7032(2016)07-0816-07

O436

A

10.3788/fgxb20163707.0816

*CorrespondingAuthor,E-mail:shenhongj2004@126.com