规范解题过程，优化整式运算

江西省南昌市育新学校 金莉莎

规范解题过程，优化整式运算

江西省南昌市育新学校 金莉莎

整式的运算是初中数学的重要内容之一，它所涉及的基础内容深，运算中变化的方式多，计算规律和法则的运用复杂。对学生学习能力和运用能力都是极大的挑战。然而这章的内容又设计在初一年级的上学期，可见它对之后的方程和不等式运算有基础和衔接的作用。所以这就要求学生在接触整式运算的初期就应该规范好解题过程，建立运算过程的思维定式，并且在定式中优化解题过程，为接下来的学习做好基础性的工作。同时规范的解题过程可以有效规避错误的发生，更有助于学生养成良好的解题思路和学习习惯。

解题过程一，识别同类项。

对于整式加减运算和之前学习的有理数的加减运算来说，最大的不同就是整式中包含的项比较复杂，可能同时包含了数字、字母以及指数不同的字母，而且各项之间会有括号的干扰。同类项的准确识别和排列是决定解题结果是否准确的基础性步骤。在这个过程前，需要打开整式中存在的括号，将各项置于同等的条件下进行甄别。属于同类项的必须满足两个条件：一是项的字母相同；二是项的相同字母的指数相同。

通过以上整式的整理步骤和同类项的识别、归属，我们已经将题目整式进行了简化。在这个过程中我们发现：所有的常数为同类项；同类项的系数可以不同；同类项中不同字母的排列可以不同。在开括号的过程中，要遵循有理数运算中符号的变化规律：括号前是负号的，打开括号后，括号内各项均需变号。所以同学们需要灵活掌握和运用同类项需满足的两个条件以及符号的变号规律。

解题过程二，排列和合并同类项。

对于整式的加减运算，合并同类项是最为关键的步骤。在这个过程中要梳理好同类项的位置关系，同时不要疏漏各项的正负号。特别是对于较为复杂，项数较多的整式运算，需要首先将题目中的各项进行有规律的排序，而这个规律需要根据题目的实际情况斟酌后选择，一般按着选定字母的升幂或降幂的次序排列。排列后运用括号将同类项进行合并，这个过程中主要依据加法交换律和结合律，同时也需运用有理数加法法则来确定同类项结果的正负符号。

仍以上题为例，第三步，按着a的降幂顺序来对整式进行排列：

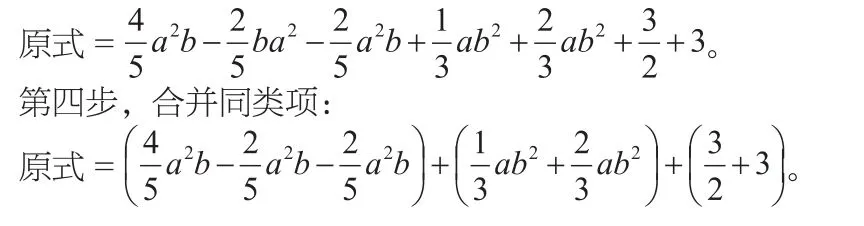
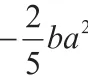
解题过程三，整式的加减运算。

通过以上四步的分析和运算过程，现在我们已经将整式进行了合并同类项，接下来的加减运算就显得简单易行了。但是运算阶段的“变术”较大，可以设计的题型较多。除了上面例题中直接进行整式的运算外，还可以变化成以下几类运算：一类是对字母赋予具体的数值，与有理数的运算相结合；另一类是整式与整式间的加减运算，如：比A整式少（或多）B整式的式是什么。其实这类变形题目并不复杂，只需按着以上规范的解题思路来逐步分析，题目就可迎刃而解。

仍以上题为例，第五步，整式的加减：

拓展1作为一道求值题，它与例题一样，首先要经过整式的化简过程，然后带入赋值求解。如果直接带入赋值求解，则会大大增加计算的步骤和难度，由于计算过程复杂，难免会出现纰漏，导致结果的错误。拓展2看似与例题无关，是一道多项式与多项式的减法题，但是将题目化简、排列整理后，会发现与例题的步骤三一致，仍然是一道基础的整式运算题。虽然整式的运算变式较多，但其遵循的解题过程是有一定规律的。所以同学们在解决这类题型的时候，不要盲目解题，而要遵循规范的解题步骤，化繁为简。

综上所述，整式的运算虽然形式复杂、可以设问的方式多，但解题有一定的规律可循。同学们在解题的过程中，如能遵循如上所述的解题的三个程序，五个步骤，规范解题的思路和过程，则在应对整式加减计算时定能从容不迫。更重要的是，整式的运算作为初中代数运算的基础，对之后的学习有很好的示范作用，养成规范的解题过程有助于帮助同学们形成规范的数学逻辑，在之后应对更困难更复杂的题目时能有章可循。希望在同学刚接触整式运算的阶段，老师能帮助同学认清规范解题过程的重要性，积极开展解题规范化教学，帮助同学养成好的学习习惯和数学逻辑，为未来的学习打好基础。