如何培养学生的自主学习能力

江苏省苏州工业园区星浦学校 卢 华

如何培养学生的自主学习能力

江苏省苏州工业园区星浦学校 卢 华

托尔斯泰说：“成功的教学所需要的不是强制，而是激发学生的兴趣。”兴趣是学习最好的老师。心理学研究表明，学习兴趣对学习效果能产生很大影响。学生学习兴趣浓厚，情绪高涨，他就会深入地、兴致勃勃地学习相关方面的知识，并且广泛地涉猎与之有关的知识，遇到困难时表现出顽强的钻研精神。否则，他只是表面地、形式地去掌握所学的知识，遇到困难时往往会丧失信心，不能坚持学习。

一、提供给学生“学”的方法，培养学生的创新能力

提供给学生学的方法，犹如交给学生打开知识大门的钥匙。学生掌握了方法，才能真正把握学习的主动权，真正处于学习主体位置。学生的创新意识，只有在自主探索问题与解决问题的过程中才能得到培养。因此，教学时应从学生的年龄特点和认知特点出发，留给学生足够的探索空间，让学生通过预习、质疑等具体活动提高创新能力。

1.指导预习，鼓励学生“主动探索”

自主学习的预习，贵在独立性，是学生独立获取基本知识的重要一环。指导预习按“扶——放”原则，起先可设置“导学提纲”以设计一系列问题的形式，在“学什么”“怎样学”两方面加以引导。

案例1 有理数加法的运算律

在小学我们知道，数的加法满足交换律，例如有5+ 3.5=3.5+5；还满足结合律，例如有（5+3.5）+2.5=5+（3.5+2.5）。那么引进了负数以后，这些运算律是否成立呢？也就是说，上面两个等式中，将5、3.5、2.5换成任意的有理数，是否仍然成立呢？

探索：

（1）任意选择两个有理数（至少有一个是负数），分别填入下列◇和○内，并比较两个运算结果：

◇+○和○+◇

（2）任意选择两三个有理数（至少有一个是负数），分别填入下列△、○和 ◇内。并比较两个运算结果：（△+○）+◇和△+（○+◇）

你能发现什么？

学生通过自己亲身实践、探索、便能顺理成章地概括出有理数的加法交换律和结合律，同时，还可以进一步得到，如果有多个（2个以上）有理数根据需要都可以交换位置，给运算带来很大的方便。

例如，（+35）+（+2）+（-35）+（-2）=［（+35）+（-35）］+［（+2）+（-2）］=0。这样，学生通过自己探索，知道了知识的联系、发生、发展的过程，同时，了解了运用这个规律可在计算中带来方便，对加法交换律与结合律的作用有了进一步认识。

2.鼓励学生独立思考，勇于质疑问难

有的学生胆小不敢质疑问难；有的学生满足于一知半解，不愿质疑问难，所以我们要创设条件，努力营造氛围激发学生质疑问难，教师要善于灵活地向学生提出探索性问题。数学教学的成效很大程度上取决于学生对数学的兴趣，一旦学生对所学知识产生了浓厚的兴趣，就不会感到学习是一种负担。孔子说：“知之者，不如好之者；好之者，不如乐之者。”要让学生愉快有效地学习数学，教师就要创设一些趣味性的问题情境，引发学生自主探索的兴趣。

案例2 餐桌椅的摆设

图1

问题：（1）若按照图1的摆法摆设餐桌椅，摆n张桌子可坐的人数是 。

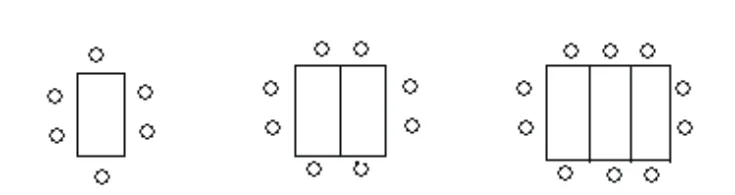
图2

（2）若按照图2的摆法摆设餐桌椅，摆n张桌子可坐的人数是 。

（3）在桌子相同时哪一种摆法容纳的人多？

（4）若你是一家大堂经理，你会选择哪种摆法？

新颖、有趣的问题立刻激发学生的求知欲，引发学生自主探索的兴趣，经过学生的探索、交流后，得出如下答案：

①单桌摆放容纳的人数最多，但餐厅面积要大；

②按照图1摆，容纳的人数虽然较多，但夹菜、交流不方便；

③按照图2摆，容纳的人数虽然较少，但便于交流，也较美观。

故应根据具体情况而定。

由学生熟悉的桌子摆设，创设趣味性的问题情境，引发学生自主探索的兴趣，通过交流合作、经历观察、比较、归纳、提出猜想过程，通过探索变量与常量的关系，初步建立这一类有规律递增问题的数学模型，不仅培养了学生的创造能力，也使学生对数学的生活化和生活的数学化都有较好的体验。

二、提供讨论交流的机会，培养交际能力

为学生提供畅所欲言，各抒己见的机会，能有效地培养学生的交际能力。引导学生自主学习，教师首先要给学生创设一个民主、平等、和谐的环境，让学生充满自信。我在教学中，经常设计小组讨论，全班交流的环节，让学生做学习的主人，充分表示自己的思维方法及过程，揭示知识规律和解决问题。这样，加强了学生之间的交往和沟通，促进相互了解，促进不断反思自己的思考过程，同时对其他同学的思路进行分析思考作出自己的判断，这种活动不仅锻炼同学们的交际能力，也增强了他的生活实践能力。这也是一种合作学习，这种合作学习给每个学生提供了表现自己的机会，不仅使自己对知识理解得更丰富、全面，而且充分放飞了自己想象力，使能力得到提高，同时也培养了学生之间团结友爱，互助合作的精神。

三、提供良好的学习氛围，激发自主学习的兴趣

教师在课堂上创造轻松、愉快的学习气氛，能使学生情绪高昂，思维活跃，学习兴趣和信心倍增，智力活跃，接受能力强。教学中，教师应积极地为学生创设一种情趣盎然的学习气氛，使学生受到陶冶、感染和激励，从而主动学习：①设疑布难，激发学生好奇心理；②巧设悬念，激发学生探知的迫切欲望；③创设情境，使学生自然产生求知的心理冲动。如：教学“正比例”时，教师领学生到操场，问：现有一根米尺，要量出旗杆的高度，怎样测量？根据旗杆的影子长也能算出旗杆的高度，影子和旗杆有怎样的关系？此后，让学生量出几种不同的杆长和各自影长，进一步研究杆高和影长的关系，进而引出“正比例”的概念。

四、提供动手操作的机会，发挥学生的主体作用

把课堂还给学生，就要让学生在课堂上有独立思考的时间。在教学过程中，放手让学生通过自己操作、实验、想象，可以让学生在主动的探索过程中发挥学生的主体作用。

案例3 数学新教材初中一年级（七年级）（上）第13页的习题6。

请以给定的图形“○○、△△、＝”（两个圆，两个三角形，两条平行线）为构件，尽可能多地构思独特且有意义的图形，并写上一两句贴切和谐的解说词，比一比，看谁说得多。例如有：