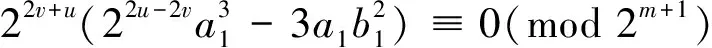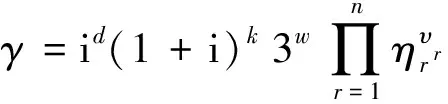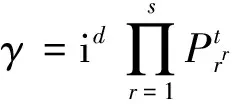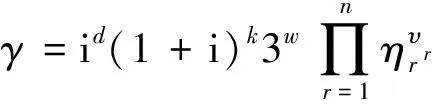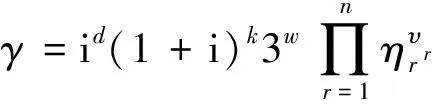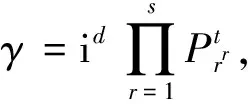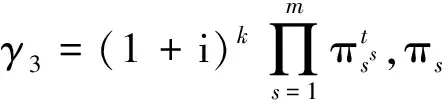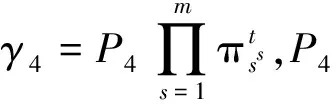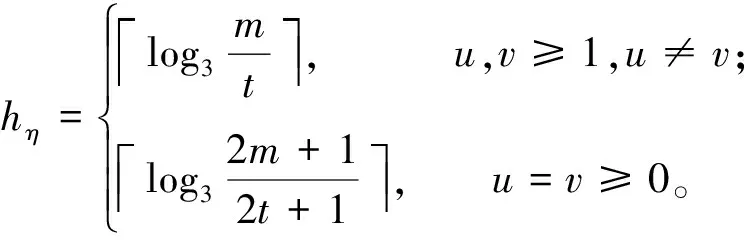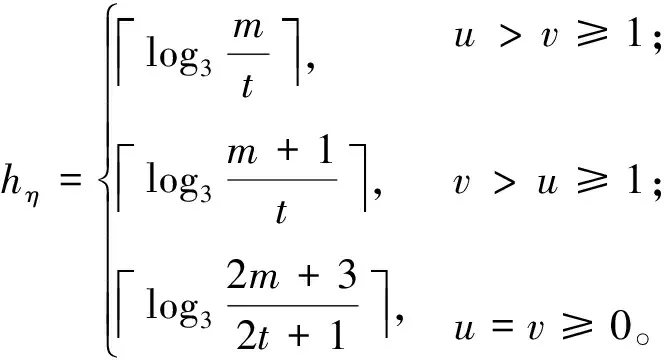模n高斯整数环的商环的立方映射图

韦扬江，梁艺耀，唐高华，苏磊磊，陈蔚凝

(广西师范学院数学与统计科学学院，广西南宁 530023)



模n高斯整数环的商环的立方映射图

韦扬江，梁艺耀，唐高华，苏磊磊，陈蔚凝

(广西师范学院数学与统计科学学院，广西南宁 530023)

Z[i]为高斯整数环，γ为Z[i]中任意非零元，〈γ〉表示由γ生成的理想。定义商环Z[i]/〈γ〉上的立方映射图G(γ)，该映射图的顶点为Z[i]/〈γ〉中的所有元素，并且，对于图中的两个顶点α和β，如果β=α3，则从α到β有一条有向边。本文对映射图G(γ)的结构进行了研究，包括G(γ)中不动点的个数，顶点0、1的入度，G(γ)的半正则性，以及任一个零因子顶点在映射图中的高度等。

高斯整数环；立方映射图；入度； 圈；半正则性

0 引言

高斯整数环Z[i]是很典型且构造特殊的一类环，在环论中占很重要的地位，由于Z[i]既融入环论的思想，同时又有数论的思想贯穿其中，国内外学者们从多个方面对Z[i]进行了研究。例如：文献[1]确定了商环Z[i]/〈γ〉中的等价类，并对该商环进行了同构分类；文献[2-3]研究了Z[i]的一些商环的立方映射图的结构；对于Z[i]的商环的单位群的研究，则在文献[4-5]中获得了完全的结果；文献[6-7]则从零因子和零因子图的角度对高斯整数环的商环进行了研究。

对于高斯整数环的商环Z[i]/〈γ〉，我们定义立方映射图G(γ)，该映射图的顶点为Z[i]/〈γ〉中的所有元素，并且，对于图中的两个顶点α和β，如果β=α3，则从α到β有一条有向边。其中 G(γ)的每一个极大连通子图叫做G(γ)的一个连通分支。显然Z[i]/〈γ〉中的单位和零因子不可能位于同一连通分支，所以可以定义G(γ)的两个子图G1(γ)和G2(γ)，其中G1(γ)是由Z[i]/〈γ〉中所有单位组成的子图，而G2(γ)是由Z[i]/〈γ〉中所有零因子组成的子图。

在映射图G(γ)中，若从顶点α到β有一条有向边，则称α为β的一个母点，而β则称为α的衍生点。我们用符号 indeg(β)表示β的入度，即β的所有母点的个数。如果α3=α，则α称为不动点。如果indeg(α)=1，则α称为孤立不动点。一个连通分支上的点如果都在圈上，则称这样的连通分支为孤立圈。

一个图称为正则的当且仅当存在正整数d，使得图中所有顶点的入度等于d。一个图称为半正则的当且仅当存在正整数d，使得图中所有顶点的入度等于d或者0。在映射图中，如果h是最小的非负整数使得β3h位于圈上，则称顶点β的高度hβ为h。如果β是圈上的点，则hβ=0。

本文研究Z[i]/〈γ〉的立方映射图G(γ)的结构，包括G(γ)中不动点的个数、顶点0和1的入度、G(γ)的正则性以及任一个零因子顶点在G(γ)中的高度。推广文献[2-3]中的相关结论。

1 相关引理

注意到Z[i]中恰有4个单位，即±1、±i。如果μ是Z[i]的单位，那么Z[i]中的理想〈γ〉和〈μγ〉是相同的，所以Z[i]/〈γ〉=Z[i]/〈μγ〉。另外，如果α是Z[i]中的素元，则μα也是Z[i]的素元。并且，μα与α称为是相伴元。

引理1(文献[1]定理3)Z[i]中的素元是以下3种形式及其相伴元：

①p，且p是整数环Z的素数，p≡3(mod 4)。

②π=a+bi，且|π|2=a2+b2=q，q是整数环Z的素数，q≡1(mod 4)。

③α=1+i。

根据引理1，若γ∈Z[i]，则

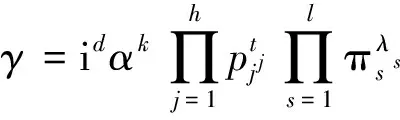
其中：d、k、h、l为非负整数；tj及λs均为正整数；α=1+i；p1，…，ph是整数环Z中的互不相同的模4余3的素数；π1，…，πl是Z[i]中互不相同的素元且|π1|2，…，|πl|2是整数环Z中的模4余1的素数。

引理2(文献[4]定理1) 令p、q、π和α是引理1中给定的元素，n为正整数，则Z[i]的商环的等价类为：

①Z[i]/〈pn〉={[a+bi]：0≤a≤pn-1，0≤b≤pn-1}；

②Z[i]/〈πn〉={[a]：0≤a≤qn-1}；

③Z[i]/〈α2m〉={[a+bi]：0≤a≤2m-1，0≤b≤2m-1}，m≥1；

④Z[i]/〈α2m+1〉={[a+bi]：0≤a≤2m+1-1，0≤b≤2m-1}，m≥0。

引理3(文献[4]定理2) 令p、q、π和α是引理1中给定的元素，n为正整数。则：

①[a+bi]是Z[i]/〈pn〉中的单位当且仅当a和b至少有一个与p互素；

②[a]是Z[i]/〈πn〉中的单位当且仅当a与q互素；

文献[4]确定了Z[i]的商环的单位群的结构，该文献例5指出：当R=Z[i]/〈(1+i)5〉 时，U(R)≌Z2⊕Z2⊕Z4。事实上，这个结论是不正确的。因为，由引理2和3可知：

U(R)={1,3,5,7,i,3i，1+2i，2+i，2+3i，3+2i，4+i，4+3i，5+2i，6+i，6+3i，7+2i}。

在U(R)中，恰有4个元素的二次方等于1，即x2≡1(mod8)在U(R)中的解为x=1,3,5,7。而且U(R)中其余元素均为4阶元。因此U(R)≌Z4⊕Z4。下面我们给出修定后的Z[i]的商环的单位群结构。

引理4(文献[4]定理3、4、5、6) 令p、q、π和α是引理1中给定的元素，n为正整数。则：

①U(Z[i]/〈α〉)≌Z1，U(Z[i]/〈α2〉)≌Z2，U(Z[i]/〈α3〉)≌Z4，U(Z[i]/〈α4〉)≌Z2⊕Z4，U(Z[i]/〈α5〉)≌Z4⊕Z4；

②U(Z[i]/〈α2m〉)≌Z2m-1⊕Z2m-2⊕Z4，m≥3；

③U(Z[i]/〈α2m+1〉)≌Z2m-1⊕Z2m-1⊕Z4，m≥3；

④U(Z[i]/〈pn〉)≌Zpn-1⊕Zpn-1⊕Zp2-1；

⑤U(Z[i]/〈πn〉)≌Zqn-qn-1。

下面的引理易证。

2 主要结论

定理1 令γ为式(1)中的形式，则对应的立方映射图G(γ)中不动点的个数L(γ)为：

证明 由引理5，只需分别求出γ是不同素元的方幂的情形时G(γ)不动点的个数即可。

①令γ=(1+i)k，容易算出L(1+i)=2，L((1+i)2)=3，L((1+i)3)=5，L((1+i)4)=5，L((1+i)5)=5。

接下来，令k≥6。首先假设k=2m，其中m≥3。这时〈γ〉=〈2m〉，从而Z[i]/〈(1+i)2m)〉≌Z[i]/〈2m〉。由文献[2]定理 3.1得Z[i]/〈2m〉不动点个数L(2m)=9，m≥3。

其次，令k=2m+1，其中m≥3。令η=[x+yi]∈Z[i]/〈γ〉并且η3=η。若η是Z[i]/〈γ〉中的零因子，由于Z[i]/〈γ〉是局部环，所以η2-1是Z[i]/〈γ〉中的单位，因此η=0。若η是单位，则由η3=η，得η2=1。由引理2得：

x2-y2≡1(mod2m+1)，

(2)

2xy≡0(mod2m)。

(3)

由引理3可知，此时x与y的奇偶性不同。如果x为偶数而y为奇数，则由方程(3)知2m-1|x。由于m≥3，故2(m-1)-(m+1)=m-3≥0。从而由方程(2)得y2≡-1(mod2m+1)，但这个方程在m≥3时是无解的。故必有x为奇数而y为偶数，此时由方程(3)可知2m-1|y。从而由方程(2)得x2≡1(mod2m+1)，且此方程在m≥3时解数为4(文献[8]191页习题7)。又因为2m-1|y且0≤y≤2m-1，故y=0，2m-1。因此由同余式(2)、(3)构成的方程组在m≥3且x与y不同时为0时恰有8个解。

所以，由上面讨论可知k≥6时，L((1+i)k)=1+8=9。

②令γ=πμ，μ≥1，|π|2是整数环中模4余1的素数。由引理2可知，Z[i]/〈πμ〉≌Zqμ，这里|π|2=q。所以只需求出Zqμ中不动点个数即可。又因为Zqμ是局部环，所以若η是零因子，由η3=η可知η=0。若η是单位，由引理2，只需求出方程x2≡1(modqμ)解的个数即可。由引理6可知，x2≡1(modqμ) 的解数等于gcd(2，q-1)=2，因为q为奇素数。所以，L(πμ)=2+1=3。

③令γ=pe，e≥1，p是整数环中模4余3的素数。由文献[2]定理3.1的讨论过程知L(pe)=3。证毕。

由上述定理的证明过程我们可以直接得到γ=(1+i)k时G(γ)中的不动点。

推论1 若γ=(1+i)k，则G(γ)中的所有不动点组成的集合F为：

①k=1时，F={[0]，[1]}；

②k=2时，F={[0]，[1]，[i]}；

③k=3时，F={[0]，[1]，[3]，[i]，[2+i]}；

④k=4时，F={[0]，[1]，[3]，[1+2i]，[3+2i]}；

⑤k=5时，F={[0]，[1]，[3]，[5]，[7]}；

⑥k=2m且m≥3时，F={[x+yi]：x=1，2m-1，2m-1±1；y=0，2m-1}∪{[0]}；

⑦k=2m+1且m≥3时，F={[x+yi]：x=1，2m+1-1，2m±1；y=0，2m-1}∪{[0]}。

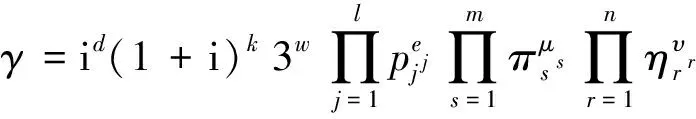
证明 由引理5，只需分别求出γ是一个素元的方幂的情形时单位元1的入度。

①令γ=(1+i)k，k≥1。易知η3=1当且仅当o(η)=1或3。根据引理4可知，3不能整除U(Z[i]/〈γ〉)的元素个数。因此indeg(1)=1。

②令γ=3w，若w=1，根据引理4，可以得到U(Z[i]/〈3〉)≌Z8。因此η3=1当且仅当η=[1]。故indeg(1)=1。若w≥2，因为在循环群Z3w-1中恰有3个元素的阶是1或3，所以由引理4，indeg(1)=32。

③令γ=pe，e≥1，p为模4余3的素数且p≠3。由于p+1与p-1恰好有一个能被3整除，所以由引理4得indeg(1)=3。

④令γ=πμ，μ≥1，且|π|2=q为模4余1的素数。由引理2，要求G(γ)中顶点1的入度，只需求同余方程x3≡1(modqμ)解的个数。由引理6可知，上述方程的解数等于gcd(3，q-1)。注意到4|q-1，从而gcd(3，q-1)=3当且仅当3|q-1，当且仅当12|q-1。所以，当q≡1(mod12)时，indeg(1)=3。当q≢1(mod12)即q≡5(mod12) 时，indeg(1)=1。证毕。

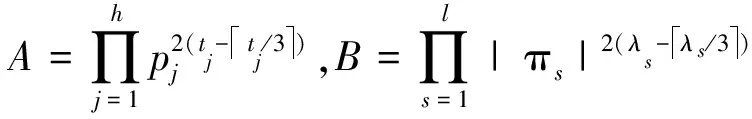
证明 由引理5，求0在G(γ)的入度，可以分别求出γ是一个素元的方幂的情形时0的入度。

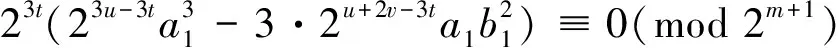
(4)

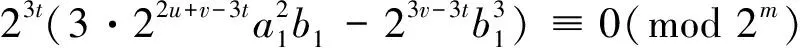
(5)

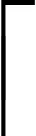
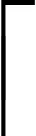
(6)

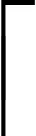
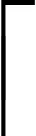
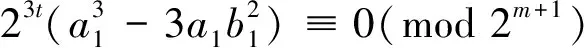
(7)

(8)

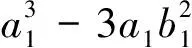
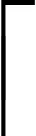
2n‖a， 2n‖b

(9)

时，η3=0。易知满足条件(9)的η共有2m+1-n-1×2m-n-1=24n-1个。

当u>v时，则t=v

(10)

(11)

2n+1|a， 2n‖b

(12)

时，η3=0。易知满足条件(12)的η共有2m+1-n-1×2m-n-1=24n-1个。

最后，假设u

定理4 令γ为Z[i]中的非零元，则：

证明 顶点1、0是G(γ)中的孤立不动点，当且仅当indeg(1)=indeg(0)=1，根据定理2和定理3直接计算便可证明定理。证毕。

定理5 令γ为Z[i]中的非零元，则：

证明 ①在映射图G1(γ)中，入度大于0的任意顶点的入度等于单位元1的入度。而当indeg(1)=1时，G1(γ)中不存在入度为0的顶点。所以indeg(1)=1时，G1(γ)中所有顶点的入度都等于1，即G1(γ)的每一个连通分支恰好是孤立圈。由定理4即可证明结论成立。

定理6 令γ为Z[i]中的非零元，则：

①G1(γ)中不包含长度大于1的圈当且仅当γ=1+i或者(1+i)2；

②G2(γ)中不包含长度大于1的圈当且仅当γ=Pk，k≥1，P是Z[i]中的任意一个素元。

证明 ①令γ=(1+i)k，k≥1。当k=1，2 时，直接验证可知G1(γ)仅包含长度为1的圈。若k>2，由于i为Z[i]/〈γ〉的单位，i3=-i≠i，且i9=i，因此i→i3→i构成一个长为2的圈。

令γ=pt，p是整数环中的素数且p≡3(mod4)，t≥1。同理可知i→i3→i是G1(pt)中长为2的圈。

令γ=πn，|π|2=q是整数环中模4余1的素数，n≥1。根据引理4，U(Z[i]/〈πn〉)≌Zqn-qn-1，这是一个循环群。令这个循环群的生成元为g，则o(g)=qn-qn-1=qn-1(q-1)。由于q≡1(mod4)，故4|q-1。令d=gqn-1(q-1)/4，则o(d)=4，d3≠d，d9=d。从而d→d3→d是G1(πn) 中长为2的圈。

所以，由以上讨论可知，当γ为Z[i]中的素元的方幂时，G1(γ)不包含长度大于1的圈当且仅当γ=1+i或者(1+i)2。当γ为Z[i]中一些素元的积时，由引理5可得结论成立。

②一方面，我们证明当γ是至少两个不同的素元的乘积时，G2(γ)中必然包含长度大于1的圈。

假设γ1=(1+i)kP1，P1是Z[i]中的若干素元的乘积，且P1与1+i不是相伴元，k>2。由中国剩余定理可知，存在η1∈Z[i]，使得η1≡i(mod(1+i)k)且η1≡0(modP1)。则η1是Z[i]/〈γ1〉中的零因子。由于i位于G1((1+i)k)的2-圈上，所以η1位于G2(γ1)的2-圈上。

假设γ2=(1+i)kP2，P2是整数环中的若干个模4余3的素数的乘积，k=1，2。由中国剩余定理可知，存在η2∈Z[i]，使得η2≡0(mod(1+i)k)且η2≡i(modP2)。则η2是Z[i]/〈γ2〉中的零因子。由于i位于G1(P2)的2-圈上，所以η2位于G2(γ2)的2-圈上。

另一方面，当γ为Z[i]中的某个素元的方幂时，由于Z[i]/〈γ〉为局部环，所以G2(γ)只有一个分支，顶点0是G2(γ)中唯一的位于圈上的点。所以G2(γ)中不包含长度大于1的圈。证毕。

易知，G1(γ)中每个顶点的入度或者等于顶点1的入度，或者等于0，故G1(γ)总是正则图或半正则图。但对于G2(γ)而言，其半正则性比较复杂。下面，我们讨论G2(γ)的半正则性。

定理7 设α、p、q与π为引理1中给定的元素，令k为正整数。则：

①G2((1+i)k)是半正则的当且仅当k<5；

②G2(pk)是半正则的当且仅当k=1，2，3且p≡7(mod12)，或者k=1，2，3，4且p≡11(mod12)；

③G2(πk)是半正则的当且仅当k=1，2，3且q≡1(mod12)，或者k=1，2，3，4且q≡5(mod12)，这里|π|2=q。

证明 ①当k=1时，G2(1+i)只有一个顶点。当0

下面令k=2m+1，m≥3。设β=(1+i)3=-2+2i，则β在G2((1+i)k)中的入度大于0。假设η=[a+bi]∈Z[i]/〈(1+i)k〉且满足η3=β，这里0≤a≤2m+1-1，0≤b≤2m-1。则有以下同余方程成立：

a3-3ab2≡-2(mod2m+1)，

(13)

3a2b-b3≡2(mod2m)。

(14)

由同余式(13)和(14)可知，a与b均为奇数。又，由同余式(13)可得：

a3-3ab2≡-2(mod2m)。

(15)

因此，根据式(14)和式(15)即有：

a4-b4≡2(b-a)(mod2m)。

由于m≥3，故3m-3≥m+1，2m-2≥m+1。因此，以上同余式可化为2md2≡0(mod2m+1)。所以，2|d2。但由于0≤b≤2m-1，故可得b=1。同理，将a=2m-1d1+1和b=2m-1d2+1代入同余式(14)，得：2md1≡0(mod2m)，则可知d1为任意整数。又由于0≤a≤2m+1-1，因此，d1=0，1，2，3。所以，由同余式(13)和(14)组成的方程组的解数为4。也就是说，η3=(1+i)3当且仅当η=[1+i]，[1+2m-1+i]，[1+2·2m-1+i]，[1+3·2m-1+i]。即，当k=2m+1且m≥3时，indeg((1+i)3)=4。但是根据引理3，此时indeg(0)=8。因此，G2((1+i)k)不是半正则的。

②由于Z[i]/〈pk〉≌Zpk[i]，因此由文献[2]定理4.2即得。

③由于Z[i]/〈πk〉≌Zqk，因此由文献[9]定理3.7即得。证毕。

最后，我们研究映射图G(γ)的零因子顶点的高度。由于文献[3]定理3.5、3.6已分别给出G2(2k)和G2(pk)的顶点的高度，这里p是整数环中模4余3的素数，因此，我们主要讨论γ=(1+i)k且k为奇数的情况。

定理8 令η=[a+bi]是Z[i]/〈(1+i)k〉的零因子，k≥1。设2u‖a，2v‖b，u，v≥0，t=min{u，v}。则η在G((1+i)k)中的高度为：

证明 因为Z[i]/〈(1+i)2m〉≌Z2m[i]，由文献[3]定理3.5，可得①的结论成立。下面当k=2m+1时证明结论②。

2t·3jaj≡0(mod2m+1)，

(16)

2t·3jbj≡0(mod2m)。

(17)

[1] DRESDEN G，DYMEK W M. Finding factors of factor rings over the Gaussian integers[J]. Amer Math Monthly，2005，112(7): 602-611. DOI:10.2307/30037545.

[2] WEI Yangjiang， NAN Jizhu， TANG Gaohua. The cubic mapping graph for the ring of Gaussian integers modulon[J].Czech Math， 2011，61(4)：1023-1036. DOI:10.1007/s10587-011-0045-7.

[3] WEI Yangjiang， NAN Jizhu， TANG Gaohua.Structure of cubic mapping graphs for the ring of Gaussian integers modulon[J].Czech Math， 2012，62(2): 527-539. DOI:10.1007/s10587-012-0027-4.

[4] CROSS J T. The Eulerφ-function in the Gaussian integers[J]. Amer Math Monthly， 1983，90(8): 518-528. DOI:10.2307/2322785.

[5] 唐高华，苏华东，易忠.Zn[i]的单位群结构[J].广西师范大学学报(自然科学版)，2010，28(2)：38-41. DOI:10.16088/j.issn.1001-6600.2010.02.004.

[6] 唐高华，苏华东，赵寿祥.Zn[i]的零因子图的性质[J].广西师范大学学报(自然科学版)，2007，25(3)：32-35. DOI:10.16088/j.issn.1001-6600.2007.03.002.

[7] 苏华东，唐高华.Zn[i]的素谱和零因子[J].广西师范学院学报(自然科学版)，2006，23(4)：1-4. DOI:10.16601/j.cnki.issn1001-8743.2006.04.001.

[8] 潘承桐，潘承彪. 初等数论[M]. 北京：北京大学出版社，1992.

[9] WEI Yangjiang， NAN Jizhu， TANG Gaohua, et al. The cubic mapping graph of the residue classes of integers[J]. Ars Combin， 2010， 97：101-110.

(责任编辑 黄 勇)

Cubic Mapping Graphs on the Quotient Rings of the Gaussian Integer Rings of Modulon

WEI Yangjiang， LIANG Yiyao， TANG Gaohua，SU Leilei，CHEN Weining

(School of Mathematical and Statistics Sciences, Guangxi Teachers Education University, Nanning Guangxi 530023, China)

LetZ[i]be the ring of Gaussian integers，γ∈Z[i]. Let 〈γ〉 denote the ideal ofZ[i] generated byγ. The cubic mapping graph G(γ) over the quotient ringZ[i]/〈γ〉 is a digraph，where the vertices of G(γ) are the elements ofZ[i]/〈γ〉， and there is a directed edge fromαtoβifβ=α3. In this paper， the structure of G(γ) is investigated. The numbers of the fixed points and the in-degree of the vertices 0 and 1 are obtained. Moreover， the semiregularity of the graph G(γ) is characterized. Finally，the height in G(γ) of an arbitrary zero-divisor is determined.

Gaussian integers; cubic mapping graph; in-degree; cycles; semiregular

10.16088/j.issn.1001-6600.2016.03.008

2016-03-03

国家自然科学基金资助项目(11461010，11661014)； 广西自然科学基金资助项目(2014GXNSFAA118005)；广西科学研究与技术开发项目(桂科合1599005-2-13)；广西高校科学技术研究项目(KY2015ZD075)

唐高华(1965—)，男，广西灌阳人，广西师范学院教授，博士，博士生导师。E-mail: tanggaohua@163.com

O153.3，O157.5

A

1001-6600(2016)03-0053-09