基于图像处理自适应变步长调焦搜索算法

王 勋，罗晓曙

(广西师范大学电子工程学院，广西桂林541004)



基于图像处理自适应变步长调焦搜索算法

王 勋，罗晓曙

(广西师范大学电子工程学院，广西桂林541004)

研究文献时发现虽然采用固定步长调焦具有调焦过程稳定的特点，但由于调焦时间较长、效率较低等问题，很难应用于实际要求实现快速调焦的系统中。现有的变步长调焦点搜索算法存在计算公式推导过程复杂、算法计算量较大等问题，在实际要求实现快速调焦的系统中，也很少使用。为了解决此问题，本文提出一种新的基于图像处理自适应变步长调焦点搜索算法。该算法的具体调焦策略：当远离最佳调焦位置时，任意清晰度评价函数上两点组成的直线与水平直线构成的夹角较小，增加调焦步长，实现粗调焦；当处于最佳调焦位置附近时，减小调焦步长，实现细调焦。最后分别使用变步长、固定步长和本文提出的基于图像处理的变步长搜索算法对不同的清晰度评价函数进行自动调焦，实验结果表明：本文提出的变步长搜索算法在保证调焦精度的前提下，可以对基于灰度时域的清晰度评价函数实现快速调焦。通过对比调焦时间发现，本文提出的基于图像处理的自适应变步长搜索算法具有调焦时间较短、计算量较小等优点。

清晰度评价函数；自适应；变步长；搜索算法；快速调焦

0 引言

在现代生物、医学仪器以及图像处理系统中，越来越多地用到自动调焦技术。其中基于图像处理的自动调焦法由于具有速度快、精度高、成本低和体积小等优点，成为现代自动调焦技术发展的主流。基于图像处理的自动调焦方法主要有调焦深度法、变步长调焦点搜索法和离焦深度法[1-3]。其中调焦深度法和离焦深度法国内外已经做了很多的研究，而且这些调焦算法从仿真结果上看，其调焦效果良好。目前变步长调焦点搜索法研究得还不够深入，本文在现有文献的基础上，提出基于图像处理自适应变步长调焦点搜索算法。现有的调焦点搜索算法常采用固定步长来寻找最佳位置，虽然可以通过设定较小的调焦步长，来得到满意的精度和调焦范围，但调焦时间较长，一般完成调焦过程需要花费10 s，无法满足实际调焦的需要[4]。在变步长调焦点搜索算法研究中，文献[5]采用任意2个位置清晰度评价函数之差的绝对值除以它们当中最大的清晰度评价函数值得到计算值M，然后将M与设定的阈值进行比较，来实现变步长。这种方法对于任意设定的初始位置，如果较远或者较近，可能会导致判误，从而增加了调焦时间。文献[6]提出基于NRSS的自适应对焦方法，然而NRSS在峰值两侧曲率变化不大，导致电机在最佳位置附近往复运动，增加了调焦时间。

现有常用灰度梯度清晰度评价函数曲线，它们的曲线总体上满足先增后减的变化趋势。清晰度评价函数曲线有两大类：一类在最佳聚焦位置曲线很陡，曲线调焦的距离范围较窄；另一类则在最佳聚焦位置曲线较平缓，曲线调焦的距离范围较宽。根据这一特点，本文采取的调焦策略：当远离最佳调焦位置时，清晰度评价函数上两点组成的直线与水平直线构成的夹角较小，增加调焦步长，实现粗调焦；当处于最佳调焦位置附近时，清晰度评价函数上两点组成的直线与水平直线构成的夹角较大，则减小调焦步长，实现细调焦。该方法不仅对陡峭的清晰度评价函数曲线具有很好的调焦效果，而且对平缓的清晰度评价函数曲线也可以实现很好的调焦。

1 灰度时域清晰度评价函数

图像清晰度评价函数是用于描述图像清晰度的一个参量，即清晰度评价函数值越大，图像越清晰，此处的位置就处于最佳的调焦位置。图像清晰度评价函数应具有无偏性、单峰性、能反映离焦特性、较高的信噪比、计算量小，同时在调焦位置附近，调焦特性曲线比较窄，更陡峭的优点[7]。理想图像的清晰度评价函数随离焦程度变化曲线如图1所示。

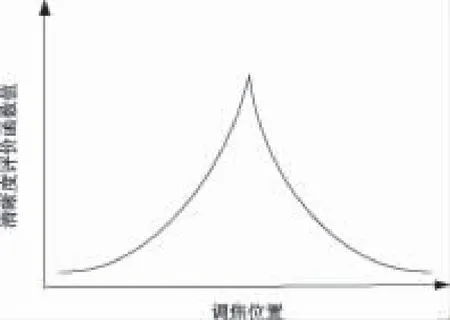
图1 清晰度评价函数随离焦程度变化曲线Fig.1 The clarity evaluation function with the degree of off focus curve

图像灰度时域清晰度评价函数包括如下常见形式[8-10](x，y表示图像的行数和列数)：

1)Variance函数

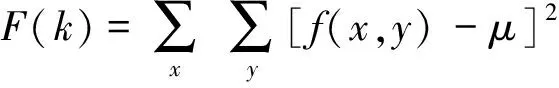
(1)

其中μ为灰度平均值。

2)灰度差分绝对值之和SMD

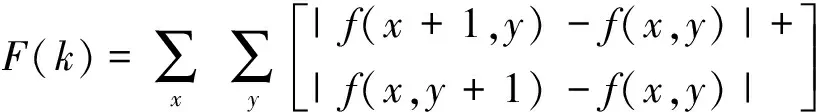
(2)

3)梯度平方函数

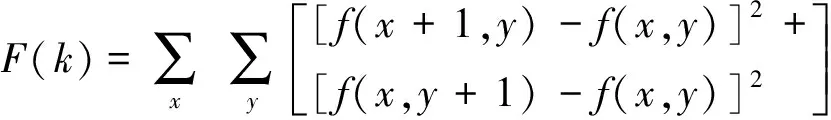
(3)

4)Brenner函数

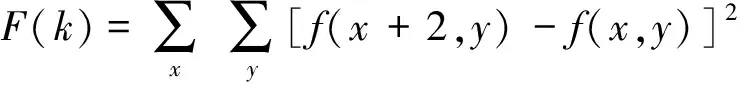
(4)

5)Laplacian函数

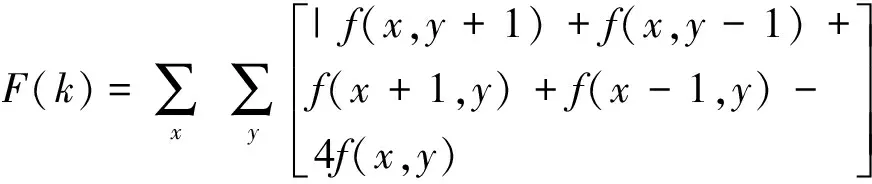
(5)

6)Tenengrand函数

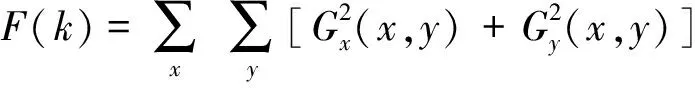
(6)

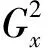
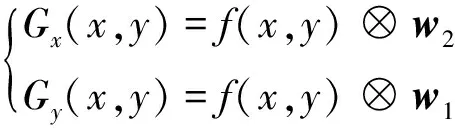
(7)

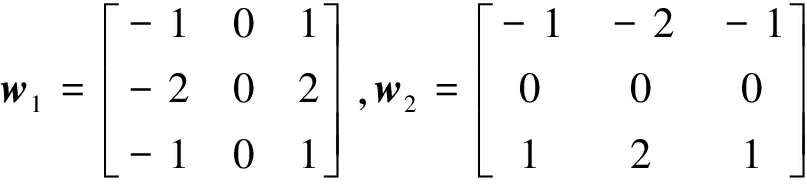
另外还有一些改进的灰度时域清晰度评价函数，这些改进的灰度清晰度评价函数一般都具有在最佳聚焦位置附近曲线更陡峭、调焦范围较窄等特点。本文基于理想的清晰度评价函数曲线，研究变步长自适应调焦点搜索算法。

2 变步长自适应调焦点搜索算法

根据清晰度评价函数计算出调焦区域内任意位置处清晰度评价函数值，需要用搜索算法找出清晰度最佳时的调焦点位置，调焦点搜索算法要求收敛速度快，同时调焦的准确度高[7]。本文对图2中的几种情况进行讨论来说明变步长自适应调焦点搜索算法的原理。假设系统任意初始位置为s0，初始位置处清晰度评价函数值为F(s0)，移动一次所处的位置为s0+l，清晰度评价函数值为F(s0+l)，取中间位置为s0+l/2，清晰度评价函数值为F(s0+l/2)。为了分析问题的方便，以F(s0)在最佳调焦位置左侧进行研究，如果F(s0)在最佳调焦位置右侧也可以得出同左侧类似的结论。

F(s0+l)与F(s0)构成的直线l1与水平轴的夹角为α：

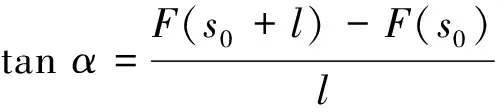
(8)

F(s0+l/2)与F(s0)构成的直线l2与水平轴的夹角为β：

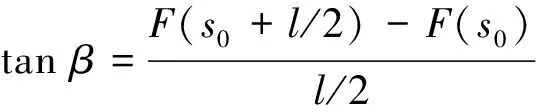
(9)

直线l1与直线l2之间的夹角为θ：

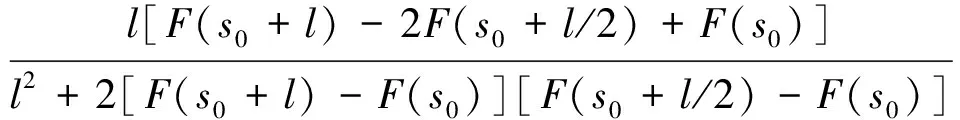
(10)

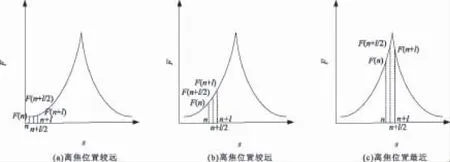
图2 清晰度评价函数值与离焦程度之间的关系Fig.2 The clarity evaluation function with relationship the degree of off focus curve

搜索过程为：

1)如果F(s0)与F(s0+l)没有明显变化，当满足式(11)、(12)、(13)、(14)和式(15)的条件时，说明任意选取的离焦位置离实际调焦位置较远，如图2(a)中所示，保持方向不变，同时调焦步长由l变为2l，继续搜索；当满足式(11)、(12)、(14)和式(16)的条件时，说明此时的位置非常接近最佳调焦位置，已经可以得到清晰的图像，停止搜索。其中在实际的测试中γ一般取值为5～10，u一般取值为85～90。

F(s0+l)>F(s0)。

(11)

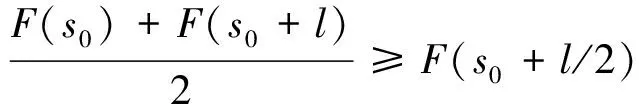
(12)

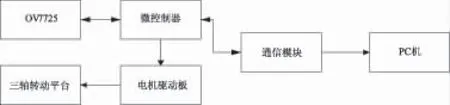
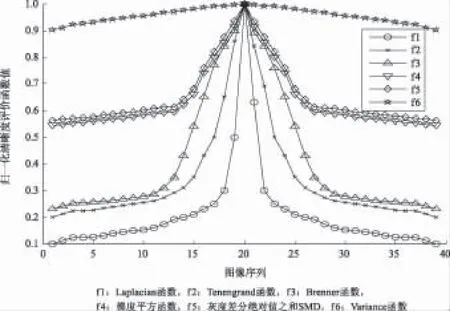
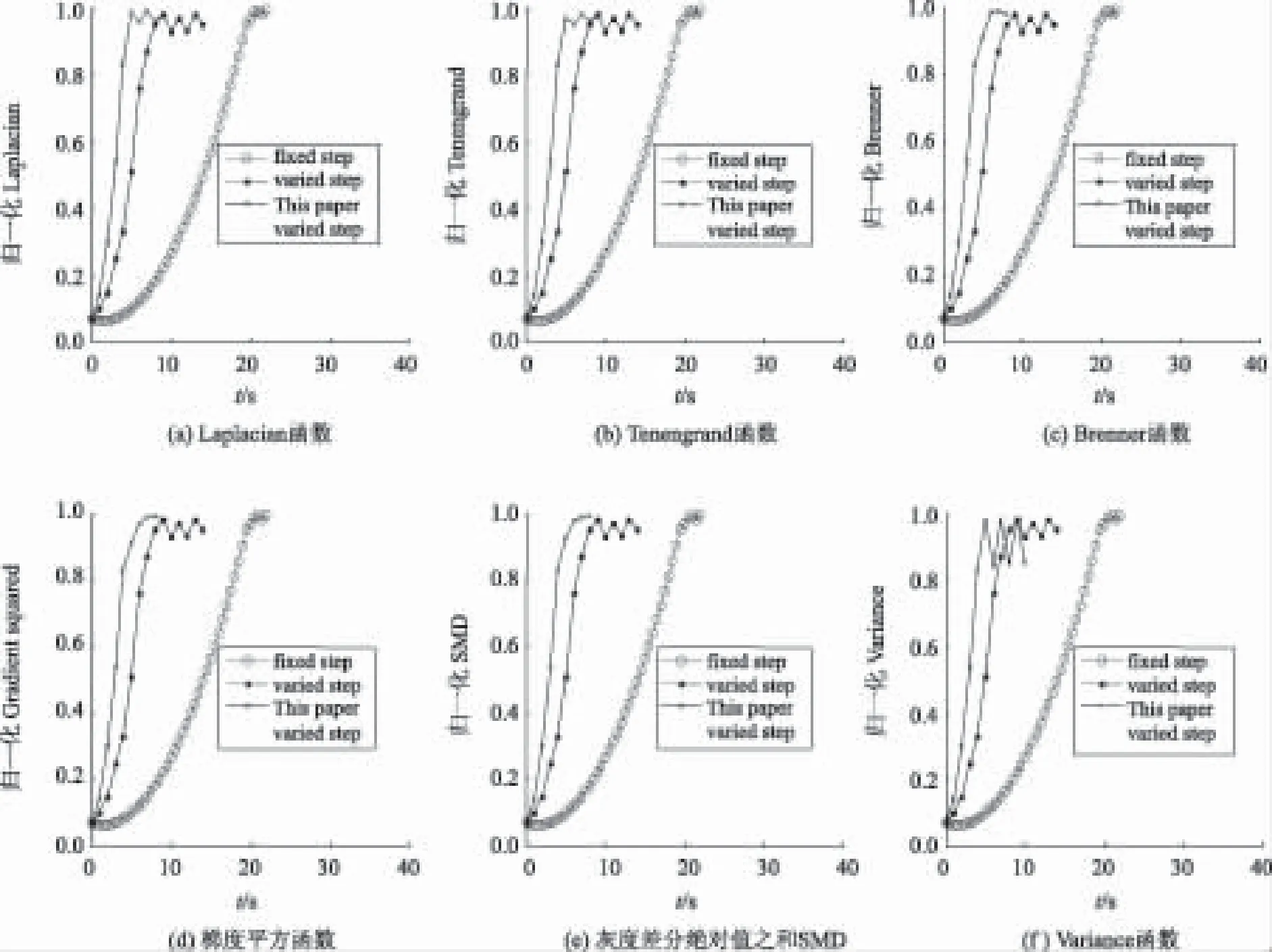
tanθ

(13)

tanα

(14)

tanβ

(15)

tanβ>tanu。

(16)

2)如果F(s0)与(s0+l)有明显增大，当满足式(11)、(12)、(17)、(18)和式(19)的条件时，表明上一次步长为l时对调焦效果影响较大，此时距离实际焦距较近，如图2(b)中所示，保持调焦方向不变，同时减小调焦步长l变为l/2，继续搜索；当满足式(11)、(12)、(14)和式(16)的条件时，停止搜索。

tanθ>tanγ。

(17)

tanα>tanγ。

(18)

tanγ

(19)

3)如果(s0+l)与F(s0)相比明显减小，当满足式(11)、(18)、(19)和式(20)的条件时，说明调焦点已经出现，如图2(c)中所示，改变搜索方向，同时减小调焦步长l变为l/2，继续搜索；当满足式(11)、(12)、(14)和式(16)的条件时，停止搜索。

(20)

3 自动调焦实验与分析

为了验证本文提出搜索算法的有效性，进行了自动调焦实验。

3.1 实验平台

搭建实验平台，该系统结构框如图3所示。其中三轴转动平台为XA07A-R1，五项电机驱动板为CRD5107P，视频采集为OV7725，微控制器采用EP4CE10E22C8N，通信模块采用USB2.0，PC机环境为CPU Pentium(R)Dual-Core E6600 @3.06 GHz，内存3 GB，软件Matlab R2011。OV7725采集视频图像，微控制器计算不同位置下每帧图像清晰度评价函数值，并通过调焦点搜索算法给出电机运动方向和步距，同时通过USB2.0传输视频图像至PC机，在PC机对每帧图像进行类似处理，观察不同调焦点搜索策略下调焦结果。

图3 实验系统硬件结构图Fig.3 Experiment system hardware structure diagram

3.2 图像灰度时域清晰度评价函数曲线实验

为了验证自适应变步长调焦点搜索算法，本文首先对图像灰度时域清晰度评价函数曲线做了调焦实验，每个序列为40幅640×480图片，归一化清晰度评价函数曲线如图4所示。从不同离焦程度图像清晰度评价函数曲线，可以看出Laplacian函数具有更陡峭的尖峰，调焦范围较窄；Tenengrand函数和Brenner函数陡峭的尖峰次之，调焦范围较宽；梯度平方函数和灰度差分绝对值之和SMD调焦范围宽且陡峭尖峰不明显；Variance函数陡峭尖峰最差。

图4 归一化灰度清晰度评价函数调焦曲线图Fig.4 Normalized grey level clarity evaluation function focusing curve

图5 3种调焦算法在不同清晰度评价函数下对比实验Fig.5 Contrast experiment of three kinds of focusing algorithms under different clarity evaluation function

3.3 调焦点搜索算法对比实验

对同一目标，电机从同一起始位置分别使用变步长、固定步长和本文提出的搜索算法进行自动调焦，并比较以上3种调焦方法的实验结果。实验中分别采用Laplacian函数、Tenengrand函数、Brenner函数、梯度平方函数、灰度差分绝对值之和SMD和Variance函数作为调焦评价函数，记录每一步调焦后清晰度评价函数值，3种调焦方式下均采用电机的最小步长作为调焦基本步长，电机每移动一个基本步长，设定为获得1帧图像，由上述理论可知u和γ的取值是可以根据具体的情况进行设置，实验发现设定γ为7、u为86调焦时间最短；对于一般变步长搜索算法，初始步长为基本步长的4倍较为合理[6，11-12]。

在图5的对比实验中，当3种自动调焦方式的最小步长相同时，固定步长调焦方式用时最长；当清晰度评价函数在最佳聚焦位置附近曲线较陡峭、调焦范围较窄时，本文提出的自适应变步长调焦搜索算法，调焦完成时间优于其他2种调焦算法。从本文提出的搜索算法的调焦曲线可以看出，当清晰度评价函数陡峭、调焦范围较窄时，调焦速度较快，但易产生循环调焦的可能；当清晰度评价函数较陡峭、调焦范围较宽时，调焦速度较快，且调焦曲线较平缓；当清晰度评价函数较平坦、调焦范围较宽时，调焦速度较快，但循环调焦时间较长。

4 结论

基于图像处理自适应变步长调焦点搜索算法和固定步长调焦搜索算法相比，其总体上调焦时间优于固定步长调焦搜索算法，而且本文的调焦点搜索算法，对于清晰度评价函数曲线不是特别陡峭，且调焦范围较宽的清晰度评价函数也可以实现快速调焦。本文的研究为下一步实现基于图像处理的自适应调焦系统提供了理论依据。

[1] 翟永平， 周东翔， 刘云辉，等. 聚焦函数性能评价指标设计及最优函数选取[J].光学学报，2011，31(4)： 04188002.

[2] 杨金峰， 赵辉， 刘伟文. 基于区域离散性的自动调焦算法[J]. 红外与激光工程， 2011， 40(11)：2286-2289.

[3] 孟希羲， 冯华君， 徐之海，等. 基于面阵CCD的时间延时积分模式的空间相机自动对焦[J]. 光学学报， 2011， 31(11)：1128002.

[4] 胡涛， 陈世哲， 刘国栋，等. 大范围自动调焦快速搜索算法[J]. 光电子·激光， 2006，17(4)：464-467.

[5] 张来线， 孙华燕， 郭惠超，等. 基于灰度梯度最大值累加的自动调焦算法[J]. 光子学报，2013，42(5)：605-610.

[6] 谢小甫， 周进， 吴钦章. 基于无参考结构清晰度的自适应自动对焦方法[J]. 光电工程， 2011，38(2)：84-89.

[7] 金雪， 马卫红. 图像调焦过程清晰度评价函数研究[J].光学仪器， 2012，34(1)：59-64.

[8] 王超， 蒋远大，翟光杰，等. 基于数字图像处理的自控显微调焦算法研究[J].仪器仪表学报，2009，30(6)： 1290-1294.

[9] 梁敏华， 吴志勇，陈涛. 采用最大灰度梯度法实现经纬仪自动调焦控制[J].光学精密工程，2009，17(12)：3016-3021.

[10] 韩瑞雨， 王晋僵，聂凯，等. 不同对比度下自适应的自动调焦算法[J].光子学报，2012，41(2)：222-227.

[11] 王钰， 石纯一. 机器学习研究[J].广西师范大学学报(自然科学版)，2003，21(2)：1-14.

[12] 王哲，钟海秀，安超，等.基于重叠区图像处理的自动调焦系统设计[J].激光与光电子进展，2015，52(4)：042801.

(责任编辑 马殷华)

Adaptive Variable Step Search Algorithm to Adjust the Focus Based on Image Process

WANG Xun， LUO Xiaoshu

(School of Electronic Engineering， Guangxi Normal University， Guilin Guangxi 541004，China)

References found that the fixed step size is used to stabilize the focusing process. However, it is difficult to be used for the practical requirements of the system due to the longer focusing time and low efficiency. In addition, amongthe existing variable step size focus search algorithms, the existing variable step size adjustment focus search algorithm has quite complex calculation formula derivation process and the computation of the algorithm is very difficult. Therefore, in the actual applications which require rapid focus, the existing algorithm is rarely used. In order to realize the fast focusing, the process of the derivation of the focusing algorithm needs to be simpleand the algorithm calculation should be simple so that the algorithm can be applied to the system of fast focusing. In this paper, the variable step size focus search algorithm is studied, and a new adaptive variable step size algorithm based on image processing is proposed. The strategy of the new algorithm is: the coarse focusing is obtained by increasing the focus step when the the system consists of a straight line of the clarity evaluation function of any two points far away from the best focusing position; a fine focusing is realized by decreasing the focus step by nearby the peak of focusing curve;finally, the variable step size, fixed step size and variable step size search algorithm based on image processing are used to automatically focus the different definition evaluation functions. Experimental results show that, in this paper, the proposed variable step size search algorithm can ensure the accuracy of the focus, can achieve rapid focus for domain definition of the evaluation function, and the adaptive variable step size search algorithm based on image processing has the advantages of shorter focusing time, less computation and so on.

clarity evaluation function; adaption; variable step; search algorithm; fast focusing

10.16088/j.issn.1001-6600.2016.03.004

2015-09-09

国家自然科学基金资助项目(21327007)；广西硕士研究生创新项目(YCSZ2015101)

罗晓曙(1961—)，男，湖北应城人，广西师范大学教授，博士。E-mail:lxs@mailbox.gxnu.edu.cn

TP274

A

1001-6600(2016)03-0025-07