一种新的求解带有非线性导体的麦克斯韦方程的有限元算法

邬丽云，王然，魏明强，康彤

(中国传媒大学 理工学部，北京 100024)



一种新的求解带有非线性导体的麦克斯韦方程的有限元算法

邬丽云，王然，魏明强，康彤

(中国传媒大学 理工学部，北京 100024)

本文引入U=∂tA，令电场E分解成E=-U-▽φ构造了一种新的基于势的有限元算法，用此算法求解了一类带指数的非线性导体的Maxwell方程，导体的非线性项为指数形式：σ(x，|E|)=|E|α-2，(0<α<1)。算法首先利用差分对时间进行离散，然后分两步循环求解U和φ，并给出收敛性和误差，最后通过两个数值实验验证了算法的可行性和有效性。

麦克斯韦方程；非线性导体；有限元算法

1 新的基于势的有限元求解非线性导体的模型

(1)

其中H为磁场强度，E为电场强度，ε是电导率，μ是磁导率。在工程背景下，可作进一步的如下假设：ε和μ在内是分片的正的常函数，且存在常数εmin，εmax和μmax，使得满足0<εmin<ε<εmax和0<μmin<μ<μmax。

为了方便起见，我们给出方程(1)的齐次边界条件：

(2)

和初始条件：

H(x，0)=H0(x) in

(3)

为了把公式(1)转化成公式A-φ，我们引入矢量势A，其定义如下：

μH=▽×A

(4)

我们记U=∂tA，则电场可以表示成

E=-U-▽φ

(5)

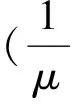
(6)

其中函数(U0，φ0)满足分解E0=-U0-▽φ0，其中U0是散度自由。对公式(4)的两边同时取旋度，考虑规范约束，那么A(x，0)=A0(x)可以通过以下的初始值问题给出：

(7)

2 时间离散变分格式

为了简便起见，首先引入一些常用符号。令L2()表示在中的平方可积函数空间，其对应的内积和范数是：

(u，v)：=∫u(x)v(x)dx和‖u‖：

用粗体表示向量值函数空间，即L2()：(L2())3。定义Hilbert空间Hm()：={vL2()：DζvL2()，|ζ|≤m}，其范数为

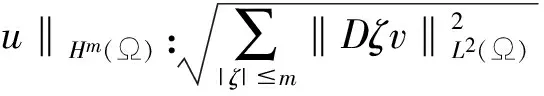
其中，m是非负整数，ζ表示非负三重指数。

令

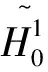
((P，φ)，(Q，ψ))v：=(P，Q)H1()+(▽φ，▽ψ)L2()

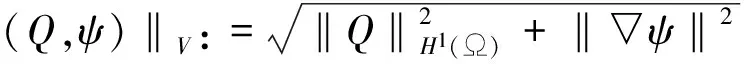
记V的对偶空间为V*。

最后，我们引入下列将在后面用到的引理。

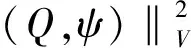
接下来，我们给出式(6)时间离散变分格式。设N是一个正整数，将区间[0，T]等分为N份，其节点ti=iτ(i=0，1，2，…，N)，其中τ=T/N。令

(8)

定理2.1 变分问题(8)对于每个i=1，2，3，…，N都有唯一解(Ui，Ai，φi)。

3 全离散格式

设是τh是上的正则四面体剖分，尺寸为h。定义

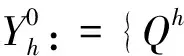
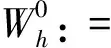
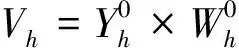
(9)

(10)

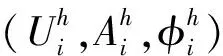
下面的定理给出误差分析结果。

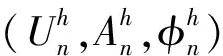
那么有

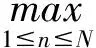
(11)

其中C是不依赖于时间步长τ和网格尺寸h的正常数。

4 数值实验

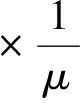
(12)

手动离散时间，在每个时间间隔我们分两步求解。

第二步：利用上一步的结果Ui，φi，求解Ai：

得到解后，求误差

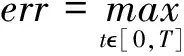
实验1：我们选取空间上为线性的真解：

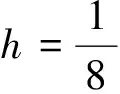
图1 空间线性的理论解相对于不同的非线性参数所得的收敛曲线

实验2：取空间为非线性函数

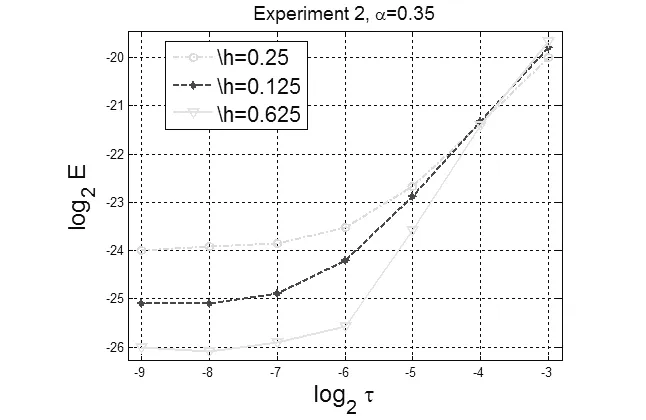
图2 非线性参数α=0.35时，取不同的网格粗细的收敛对比曲线

图2的数据可以明显的看到，当τ比较大时，误差随着τ的变化比较明显，但是当τ减小到一定程度时，误差将趋于常数，而该常数值的大小与h有关，这与误差估计的理论结果相符。

5 总结

我们引出了U=∂tA求解非线性涡流问题的A-φ有限元方法，通过时间上做差分，空间上用有限元的算法设计，给出了其收敛性和误差估计，最后对通过两个数值实验验证了算法的收敛效果。

[1]S Durand，M Slodicka.Fully discrete finite element method for Maxwell’s equations with nonlinear conductivity[J].IMA J Numer Anal，31(2011)：1713-1733.

[2]T Kang，T Chen，H Zhang，K I Kim.Fully discrete A-φ finite element method for Maxwell’s equations with nonlinear conductivity[J].Numer Meth Part D E，30(2014)：2083-2108.

[3]Susanne C Brenner，L Ridgway Scott.The Mathematical Theory of Finite Element Methods，Second Edition[M].NY：Springer，2007，60-62.

[4]胡建伟，汤怀民.微分方程数值方法(第二版)[M].北京：科学出版社，2011，247-248.

(责任编辑：宋金宝，昝小娜)

A New Finite Element Scheme for Maxwell’s Equations with a Power-law Nonlinear Conductivity

WU Li-yun，WANG Ran，WEI Ming-qiang，KANG Tong

(Science School，Communication University of China，Beijing 100024，China)

In this paper we use U=∂tA and decompose the electric field E to -U-▽φ.A new finite element scheme for Maxwell’s equations with a power-law nonlinear conductivity is built.The domain consists of some subdomainscoccupied by a nonlinear material with the electric conductivity which is supposed to be a monotone function of the power-law form |E|α-2，(0<α<1)).For each time step，we use difference scheme U and φ would be solved sequentially.We present some numerical experiments to verify the theoretical schemes.

Maxwell’s equations；nonlinear conductivity；finite element scheme

2016-07-01

邬丽云(1977- )，女(汉族)，山西人，中国传媒大学博士研究生、副教授，E-mail：wuliyun@cuc.edu.cn.

O212.4

A

1673-4793(2016)06-0023-06