波科学理论的改进
黄志洵,姜荣
(1.中国传媒大学 信息工程学院,北京100024;2.浙江传媒学院,杭州310018)
波科学理论的改进
黄志洵1,姜荣2
(1.中国传媒大学 信息工程学院,北京100024;2.浙江传媒学院,杭州310018)
波动是物质存在的一种形态,又是物质运动的独特形式。波科学研究经典波动和量子波动,而这二者不能截然分开。例如电磁波既是宏观的经典波,又是与微观世界相联系的波;这反映在光子身上,它是一种独特的微观粒子。1926年Schrödinger创造了量子波动力学,Schrödinger方程成为反映量子世界运动规律的基本方程。量子力学中波函数的复杂化来源于非经典波动的复杂性;通常认为光子是电磁场量子,但似不应把光子等同于电磁波。如光子也像电子那样(波动性有统计性质),它与经典电磁波确实不完全一样,讨论“光子的几率波方程问题”并不为错。故我们说光子至今没有自己专属的波函数和波方程,因而无法确切地代表和呈现光子奇怪的特性。
波科学;波动力学;经典波动;量子波动;电磁波;引力波;光子
1 引言
波动是自然界普遍存在的现象。人类早期观察较多的可视波动是水面波、由弦或膜的振动导致的机械波、田野里的麦浪。后来逐渐认识了一些不可目视的波动,如声波、电磁波、光波。20世纪的研究深入到微观层次之后,发现了物质波(如电子运动伴随的波动),又提出了几率波。波动的参数包括波长、频率、振幅、相位、速度、能量等。波可定义为“媒质中某种扰动的动力学过程”,扰动足够小时就得到线性波。扰动较大时波可能呈现非线性;例如:以超声速飞行的飞行器在空气中造成的冲击性声波;强电磁场在晶体中造成的参量振荡、参量放大、倍频现象等,都是非线性波。
波动力学(wave mechanics,WM)的发展源远流长,最早发端于最小作用原理,该原理可以说是“众理之母”。对波动力学贡献最大者是物理学家Erwin Schrödinger,其次是Louis de Broglie;前者提出的Schrödinger方程(SE)不仅用于处理微观粒子的运动,而且早已用来分析一些宏观科学技术问题。Schrödinger本人没有来得及在有生之年研究非线性Schrödinger方程(NLS);而de Broglie却曾致力于非线性波动力学(NLWM)的研究,并将其与孤立波联系起来。
在力学中,Hamilton原理对质点运动的描述与Fermat原理相似,这表示大自然似乎有着同样的规律。Schrödinger认为应把质点的力学过程建立在波动力学的基础上,并且指出,Fermat原理的局限性已日益显露:它无法对波动过程作精确的研究。特别是,当力学系统的尺寸很小,例如原子这样的微小系统,旧的观点和方法会失效。
1926年Schrödinger[1]发表了4篇论文,建立了非相对论性量子波动力学(QWM);他的工作承前启后,顺乎自然,沟通微观与宏观,我们给予高度评价。de Broglie和Schrödinger的工作,使波科学(wave science)研究从经典波动过渡到量子波动的层面。
2008年黄志洵[2]发表文章“波动力学的发展”,其中涵盖的方面有:波动力学基础;波方程早期发展;非相对论性波方程;Schrödinger波动力学;用Schrödinger方程分析缓变折射率光纤;波浪理论及水面孤立波;非线性Schrödinger方程;逆散射变换法;等等。2011年、2014年[3]黄志洵分别推出《波科学的数理逻辑》、《波科学与超光速物理》二书,表明其对波科学的高度重视。……现在的这篇文章,主要内容为:波科学发展的历史回顾;波科学理论的深刻化和现代化;从波科学群速公式看理论对实验的指导;光子的波方程、波函数问题;光脉冲的负波速传播;Bose双三棱镜中的消失波;引力波存在性问题。因此,本文在较宽阔的背景上展示了波科学研究的现状和改进,给出了这一学科的进步所带来的收获和深刻的启发。
2 波科学发展的历史回顾
1687年出版的《自然哲学之数学原理》是Newton的最重要的科学著作[4],是对经典力学的第一部系统而完整的著述,也是历史上第一个关于物质和宇宙的科学理论体系,其中明确定义了质量、动量和力,提出了运动学的三大定律。Newton以洞悉的目光看出维系行星运动的力与地面上使物体改变速度的力在本质上是相同的;他建立的万有引力定律(Newton反平方定律)至今仍是无可怀疑的客观规律,被各种实验一次次地证明其正确性[5]。
但是Newton的理论限定在描述有形状和质量的物质的运动,缺少对波动的思考和研究。虽然他早在1666年就磨制了玻璃三棱镜来研究太阳光的光谱,但并不表示他对光的波动性有深刻认识。1690年C.Huygens提出“光是一种波动”;1802年T.Young做了光的双缝干涉实验从而为光的波动说提供了证明;这都是在Newton视野以外的后续发展。经典力学的核心是研究在Euclid空间中的物质运动。Newton当然会注意到水波和麦浪,但并未考虑这与他建立的经典力学理论的关系。波动是物质运动的一种形态,对此人们没有异议;但波本身是否也是一种物质?或者说物质的定义是否需要和可以广义化,使之包括粒子(物体)和波动?这是一个尚待确定的问题。……尽管如此,我们已可看出所谓“波粒二象性”(wave-particle duality)这一著名课题,是涵盖在最基本的概念之中的。
Newton最先提出动量(momentum)这个在当时全新的概念,300多年后的今天,它仍具有根本的重要性。Newton在其著作的开篇即提出了“物质的量”的定义和“运动的量”的定义;前者是物质含量的多少,可由密度和体积求出(现代写法是m=ρV);后者是物质运动状况的标志,可由质量和速度求出(现代写法是p=mv)。这些今天的常识,在早先却是高度概括的简洁定义,是提出者天才的标志。
力学包括静力学和动力学,是物理学的基础。一般认为力学研究质点的运动规律和宏观物体(小到石头大到行星)的力学效应。经典力学(classical mechanics,CM)是经典物理学的基础,量子力学(quantum mechanics,QM)是现代物理学的基础。经典力学方程是数理方程中的首要内容,它有3个互相等价的系统;Newton力学,Lagrange分析力学,Hamilton动力学。这里写出3位大师的生卒年份;I.Newton(1642~1727),J.Lagrange(1736~1813),W.Hamilton(1805~1865);他们是处在17世纪中叶到19世纪中叶的人物,绵亘约200年。
从1687年到1835年(这年W.Hamilton出版了书《动力学的一般方法》[6]),是CM奠基时期,也是波科学有重要发展的时期。经典力学在今天仍然极为重要,而且CM也是QM得以建立的前提。例如Hamilton量(或叫Hamilton函数) H,既是表示总能量的函数又是动力学变量的函数,在QM的阐述中不断地使用。E.Schrödinger曾说:“如果你要用现代理论解决任何问题,首先要用Hamilton体系来表达”。
波动既是物质存在的一种形态,又是物质运动的独特形式;“波科学”的重要性不言而喻。作为物理学基础的力学怎样处理波动?波动力学(wave mechanics,WM)或许可以认为在1760年时就有了;166年后(即1926年)由Schrödinger创立了量子理论的波动力学。因此前者可称之为经典波动力学(classical wave mechanics,CWM),后者可称为量子波动力学(quantum wave mechanics,QWM)。先看CWM的情况。1760年L.Euler给出了任意波动的波方程[6]
(1)
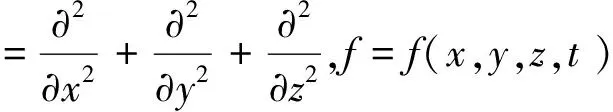
f(x,y,z,t)=F(x,y,z)ejωt
(2)
式中ω是角频率:代入到Euler的波方程,可得标量Helmholtz方程
▽2F+ω2F=0
(3)
这时Maxwell方程组还未出现。当然,电磁学的长久发展和进步的结果便是J.Maxwell[7]于1865年提出电磁场方程组,并由此推出了电磁波的波方程,其现代写法为
(4)
式中Ψ可为电场强度或磁场强度,而Ψ=Ψ(x,y,z,t);这与Euler的波方程是相同的。所以,波方程的微分形式既简单,又概括了力学、声学、电磁学这些领域的波动,显然也可以用到光学。……但是,我们注意到,在这些波方程中缺少CM的一些基本元素——质量(m)和动量(p)。
进入20世纪后,科学家们最关注的是如何理解陆续发现的微观粒子(原子、电子、光子),希望对物质结构有清晰而深刻的看法。在1911年,原子内的情形仍被看成行星系般的结构,而这并非一个合理的模型。1913年N.Bohr提出了原子能量离散化的理论,又使Planck常数h扮演了一定的角色。1924年L.de Broglie提出了“电子有波动性”的思想。……终于,在上世纪20年代,作为对微观粒子问题的长期探索的结果,也作为一种新的思维方式和新力学,量子力学(QM)横空出世。它是人类认识发展的第三个层次(前两个层次是经典力学和波动力学),意义极为重大。
1925年W.Heisenberg提出了矩阵力学与对易关系;1926年Schrödinger提出了波动力学和波函数,又解决了波动力学与矩阵力学的数学等价性;这时QM的主体部分成型了。从1926年到1927年,M. Born提出了波函数几率诠释;Heisenberg提出测不准关系式;N. Bohr提出关于波粒二象性的互补原理——这些构成QM的Copenhagen解释。1927—1928年构建了基本的量子场论(QFT):P.Dirac的电磁场量子化和电子波方程;E.Wigner的QFT基本理论。三年之中,QM理论一气呵成,闪闪发光,令人叹为观止。
经典力学(CM)的世界观是确定性(definity)的。正如Laplace据说,世界的未来可以由过去决定。意思是说:只要有边界条件和初始条件,人们即可通过求解微分方程掌握事物演化的轨迹。QM的出现使CM受到打击,例如:
①QM对物质、世界、宇宙持有独特的看法:在量子世界中测量将改变观察对象,而不做观察测量又无法获得认识,因而人们对“客观实在”的理解将变得模糊而不确定。如果说,客观实在本身在一定程度上取决于人对观察测量所做的选择,那么传统上认为客观世界与人无关的观念就将失效。正是这种情况曾使Einstein生气地说:“当我不抬头望月时,那月亮是否存在?”
②QM认为不存在因果间的直接关系,经典物理学中奉为金科玉律的确定性因果律,对量子世界不再正确,因为事件与时间并不一定保持连续性、和谐性的关系,而可能突然、间断地变化。故事件常常不可预测,几率思维取代了因果思维。这种情况也使Einstein生气,他说:“上帝不掷骰子”(实际上大自然确实像在做掷骰子游戏,因为人们只能谈论事件发生的可能性而非必然性)。
③QM认为微观粒子可以从“无”中借来能量并超过更高的能量屏障,即势垒,其理论基础是W.Heisenberg的不确定性原理(测不准关系式),而这个现象被赋予“量子隧道效应”的名称。
④QM还认为“真空不空”;正如J.Wheeler所说,真空里有剧烈的物理过程发生。量子理论的真空观不但与经典物理学不同,与相对论也不一样,其观点已为反物质的发现而证明是有道理的。使用不确定性原理,可以证明在极短的时间内可以违反“能量守恒”,例如10-13s时间内一个电子和一个正电子可以从“无”中突然出现,然后又相互结合而湮灭。此外,在真空中会不断产生、又不断消失虚光子对。真空中的起伏、涨落无论在宇宙学中或在粒子物理学中都极为重要。
⑤QM认为超光速是可能的,甚至无限大速度(物质间的超距作用)都有可能,这就是非局域性(non-locality,也译非定域性)现象。有的信仰Einstein局域性实在论的物理学家承认,由于A.Aspect的实验否定了Bell不等式,又由于近年对quark幽禁问题的研究结果表明基本粒子之间存在远距离相关,不仅西方科学家一般倾向于非局域QM,这些物理学家也不得不“容忍”非局域QM的存在,因为它“似有实验支持”。
如此等等;…… …… ……
物理学发展的三个层次突出了一个问题:如何看待物质和波动的关系?Newton力学中的物质,有形状、大小、质量和密度,受力后会运动并在空间描出其轨迹。波动却没有Newton定义的那种质量,不能用力使其加速;波展布于广大的空间,要作精确描述需用其他方法(波方程就是一种方法,现代电磁理论中的并矢Green函数、矢量偏微分算子等数学工具是另外的方法)。当然波科学的理论还没有完全搞清楚“波(动)粒(子)二象性”问题。作为最简单的理解,我们只能说光具有波粒二象性;有质量的实物粒子(如电子)也有波动性的一面,称为物质波或de Broglie波。L.de Broglie关系式为
(5)
(6)
E、p为粒子的能量、动量,f、λ为对应的物质波频率、波长。应当指出,对于光,有以下方程成立:
fλ=c
(7)
因此对于光两个关系式并非互相独立,实际上只有一个关系式;对实物粒子而言两个式子则是彼此独立的。
总之,QM的出现极大地改变了物理学思维方式,而波粒二象性是量子化的根源。对经典力学中的物质和波科学中的场与波作持续而深入的研究已成为物理科学的基本任务。当然,必须把经典性波动(如宏观条件下的声波)和量子性波动(如电子造成的物质波)区别开来。那么电磁波是经典波动还是量子波动?这问题较难回答。
1926年上半年E.Schrödinger创造了QM的波动力学,即QWM;其核心是描述微观粒子体系运动变化规律的基本运动方程——Schrödinger方程。M.Planek认为该方程奠定了量子力学的基础,如同Newton、Lagrange和Hamilton创立的方程在CM中的作用一样。Einstein的说法稍有不同,他相信Schrödinger关于量子条件的公式表述“取得了决定性进展”,但Heisenberg和Born的路子则“出了毛病”。Einstein为什么比较喜欢Schrödinger的工作而总对Heisenberg的工作抱有反感,可能是因为他认为前者的理论并非完全抛弃确定性的,与后者对确定性的决绝态度不同。当然由此也可知道,Newton的经典力学和Einstein的相对论力学,都是确定性的理论。
与经典的电磁波方程不同,在Schrödinger方程(SE)中出现了粒子质量m;如果这情况还不足以使人们感到惊讶,那么下述事实一定会引起震惊——在推导SE使用了Newton力学(即CM)中的基本动能方程[1]:
(8)
式中m、p分别为粒子的质量、动量。这就看出QM对CM的依赖(即继承性)证明“波科学研究(即使针对量子波动)不能脱离经典力学(CM)”。Schrödinger由此出发再利用算符变换(E→jħ∂/∂t,p→jħ▽)得出结果;而不是使用相对论力学方程
(9)
而在Newton力学中质量m与速度v无关。可见SE中的m并不一定是静质量m0;假定使用光子的运动质量:
(10)
那么把SE用于光频的障碍似乎并不存在。……总之,SE比Maxwell方程组高明之处在于,它描述了物质粒子与波动这两种物质形态之间的相互作用关系。但传统上认为光子不是物质粒子,因此总有物理学家对“SE也适用于光子”心存疑虑。
笔者的看法是,到20世纪的后期已有证据显示Schrödinger方程适用于光子:首先是微观粒子向势垒入射时用一维Schrödinger方程的分析(该分析证明垒内是消失态)[8],这里的“微观粒子”是包含光子的;并且,其效果有1993年的SKC实验[9]可以作证。其次,在缓变折射率光纤分析中的WKB法就是应用Schrödinger方程来分析计算的[8],而光子的运动是光纤中的基本过程。因此Schrödinger方程对电子、光子的行为作了精确的描写,波函数的量子语言取代了粒子轨道的经典语言。
3 波科学理论的深刻化和现代化
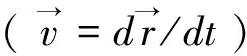
Newton力学和Einstein的相对论力学都是经典理论。狭义相对论(SR)和CM一样,处理的是实物(粒子或物体)的运动,SR即使讨论电子运动也不是采用微观的方法;广义相对论(GR)虽然讨论引力波,很大程度上也是对电磁波理论方法的模仿。针对实物(而非针对波动)的理论常常在波科学研究中出“麻烦”,SR的光速不变原理就是如此。……总之,我们认为在考虑“波科学理论的改进”时,必须分析Newton力学(CM)、Maxwell场论、相对论和量子力学(QM)之间的关系。
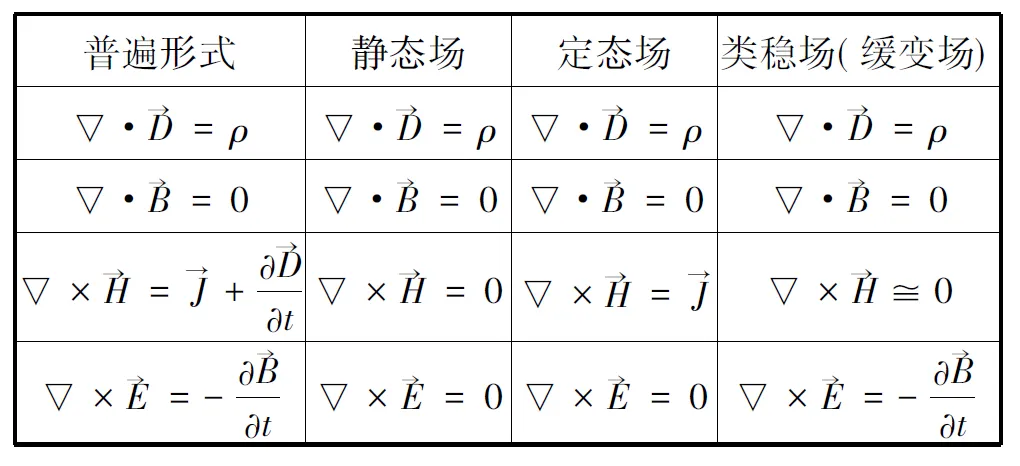
表1 Maxwell方程的比较
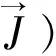
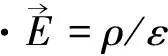
(11)
(12)
而矢量偏微分算子理论,把电磁场分开为两组互相正交的场:
(13)
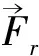
▽2φm+k2φm=-ρm
(14)
▽2φn+k2φn=-ρn
(14a)
在无旋场情况下,可按下式求场强:
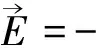
(15)
(16)
总之我们看到,改进波科学理论需要使用现代数学方法。
另一个问题是:我们已强调量子理论对波科学发展的意义,那么“改进波科学”是否需要以相对论为指导(或寻求其帮助)?宋文淼认为答案是否定的。相对论的基础是“时空一体化”,其实计量学中根本没有与spacetime(译作“空时”或“时空”)相对应的物理量及量纲。文献[10]指出,在实物运动方面,仍然是时、空分离的Newton方程。对于波动,波函数中的时、空联系表示在精确描述波的运动时不能把时空联系分开,但这也不是SR中的“4维几何关系”。4维时空把时间坐标变换为量纲与空间相同;但在SR中,各种与速度有关的关系式均为在惯性坐标系中——即1维条件下导出的。文献[10]对所谓“Minkowski 4维时空”作了尖锐的批评和精辟的论述,指出迄今人类一切活动均在3维几何空间进行;4维时空是一种探索,可以存在,但不应当作一种物理实在“推销”给大众。实际上,相对论者无法举出那怕一个例子,证明某个现代工程技术所创之物并非在3维空间做出,而必须应用4维时空理论。SR描绘的并非现实世界,GR的理论结果无一经得起推敲。例如“光线通过引力场时的弯曲”的解释,其实电磁波束进行中总是逐步扩散开来,在被物体遮挡后弯曲,即绕射。但在当今关于绕射的上千篇论文中,没有一个讲绕射现象“与绕射体的质量有关”。GR有很大的逻辑缺陷,整个相对论来自缺乏物理依据的假设。至于GR应用在现代宇宙学,奇点、百亿年前的“事件”都非实验观察可以检验,是无意义的。
Minkowski“4维时空”概念的不合理性还在于,空间的3个元素(坐标)与时间在数学上没有统一的运算规则。前者可以构成物理上实在的矢量,而时间是一个看不见的概念性参数,硬拉在一起既无严格数学特征又没有物理意义。时间、空间应保留各自的独立性,实际上复域中所有的波函数都是时空分离的。完全否定Newton不会为人类提供有用的知识。
4 从波科学群速公式看理论对实验的指导
近年来,科学界开展了对“负波速”现象的研究[11]。在宏观世界的CM条件下,由于速度是矢量,“负波速”通常被认为是“运动方向反了过来”。但在波科学中事情却没有这么简单。首先,波速被认为是标量而非矢量[12];其次,负速度可能对应负时间。这就引起了复杂的讨论,例如涉及是否存在“超前波”(advanced waves)的问题。……2000年《Nature》发表了王力军(L.J.Wang)等[13]的著名论文,报道了他们完成的负群速 (NGV)实验,我们称为WKD实验。然而几年前有物理学家说“该实验的理论公式计算有问题”;本节对此作分析讨论。
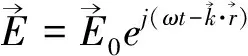
(17)
仅考虑大小时有
(18)
而波矢大小k代表相位常数,即k=β,故有
(19)
而对已调波而言,包络的相速代表波群速度,称为群速;可以证明下式的合理性:
(20)
式中ω0是载频;上式也写作
(21)
把ω=βvp代入,得
(22)
这个关系也称为Rayleigh公式。
现在把折射率概念引入到推导和计算中,即取
(23)
式中c是真空中光速,而相折射率n为
(24)
式中εr=ε/ε0,μr=μ/μ0,而ε、μ是媒质的介电常数和导磁率,并且c=(ε0μ0)-1/2;这些关系式都是严谨的,来源于Maxwell的电磁波基本理论。
在以上的严格定义和推导的基础上,可以设法计算vg与n的关系。作为一个重要步骤,我们先求相位常数β:
(25)
把β代入vg公式,求解
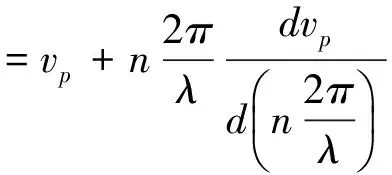
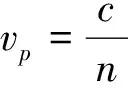
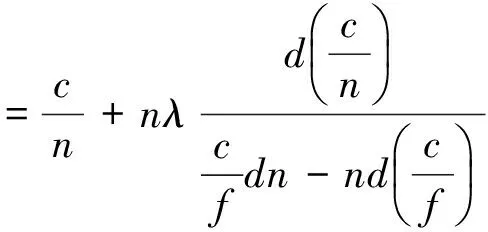
上下同乘f/n,得
(26)
此公式是严格的,不含任何近似。
会发生错误的推导举例如下;从(22)式出发,取β=2π/λ,则
故
取vp=c/n,则
故
把λ=c/f代入,得
(27)
此式与公式(26)明显不同。
这个推导错在取β=2π/λ;而我们在(25)式中已严格地证明β=2πn/λ。由于λ满足λf=c,在这里λ的意义是真空中波长。如果一定要取β为2π与波长的比,那么必须使用媒质中波长λ′,其值为
(28)
故可得
(29)
这时结果与(25)式相同。
(26)式是唯一正确的公式,给实验工作以基本的指导。在正常色散时dn/df>0,故在一般的(n>0的)条件下vg
(30)
这时vg=∞,是无限大群速。获得负群速(NGV)的条件是
(31)
在n>0时,必需是反常色散才有满足上式的可能,即要求
(31a)
而且反常色散要足够强。这些论断已被近年来的许多实验所证明。
现用数据计算说明不同的推导会导致对WKD实验作出不同评价。取f=3.48×1014Hz,Δf=1.9×106Hz,n=1,Δn=-1.8×10-6,可算出
这根本得不到负群速,WKD实验不成立。因此下述公式完全错误:
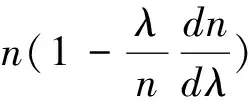
(32)
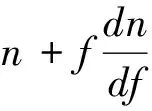
(33)
注意这些近似号!必须认识到公式(26)是严格的,由之而来的下式
(26a)
也是严格的(不带有近似号),WKD实验才能正确解释。实际上,该实验并未像有人所说的那样发生理论基础上的错误。
故WKD实验的正确表述如下:设样品(气室)厚度为L,真空时光通过时间为L/c,内装实验用铯蒸汽时通过时间为L/vg,故时间差为
(34)
已知L=6×10-2m,c=3×108m/s,故L/c=2×10-10s=0.2ns;实验测得(-Δt)=62ns,故得
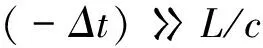
结论是,对WKD实验可以有不同看法及评论,但说“该实验的理论基础有问题”则不对。我们的推导和计算把这件事完全弄清楚了。
5 光子的波方程、波函数问题
1925年Einstein高兴地访问巴西,没想到在巴西科学院的一场演讲出了问题。当稿子讲完后,有听众提出了以下问题——过去一直认为光是波动,而现在又说“光由光子组成”;然而波伸展在整个空间,而粒子却是分立的实体,如何从数学上和概念上统一这两者?……Einstein回答不出来,场面弄得尴尬。
QM的发明是现代物理学开始建立的标志;然而在1925年还没有QM。大家都知道Einstein成长的背景是19世纪的传统物理学,用这些来回答听众的提问是不可能满意的。在Einstein巴西演讲的一个月后,W.Heisenberg发明了一种新的物理学,即量子力学。Einstein看不到(不能看到又不想看到)的要点是,光子不是一个经典的东西。1925年5月7日在巴西科学院作报告的那个夜晚,标志着Einstein作为前沿科学家生涯的终结。直到去世,Einstein都不接受量子力学,该理论用不确定性取代确定性。Einstein在里约热内卢的演讲表示他仍希冀他于1905年放出的“妖怪”(光子)还可用老的经典物理去驯服,那当然是办不到的。实际上,即使在今天(QM提出已90年)科学界也没有完全弄清楚光子到底是什么[14],1925年Einstein回答不了听众的提问亦不足为怪。
前已述及,Newton创立的CM建筑在质量、动量定义的基础上。在QM中,与此对应的是波函数(wave functon)。这个概念在经典波动中其实也有,但只有在QM中方显得特别突出。先看经典波动中的波函数,例如电磁波中的均匀平面波,电场分量写作:
Ex(z,t)=Re[Ex(z)ejφxt]=Re[E0ejφx·e-jkz·ejωt]=E0cos(ωt-kz+φx)
(35)
这里z是波传播方向,k=2π/λ是波传播单位距离的相位变化,e-kz因子的部分解代表向正z方向传播的波,φx是初始相位。这种波表示法对经典力学也一样,例如对弹性波可以写出
(36)
这是时间因子ejωt的写法。如取e-jωt,写法应为
(37)
两种写法在本质上并无不同。这里ψ表示一种扰动随时间、空间的分布状态,例如在弹性波中ψ表示质点离开平衡位置的距离,而在电磁波、光波的情况下ψ表示电场或磁场的某一分量。波动的描写方法与描述质点的力学方法(坐标、动量)是很不相同的。
QM中波函数的复杂化来源于非经典波动的复杂性,这里可以比较光波和与电子运动相伴随的波动。电磁波传播时展布于空间的波动是有能量的客体,具有物质性特征。与此相对照,电子的物质波仅为几率波(probability waves)。波函数最早由Schrödinger提出,但他过份强调波动性,认为一切物理现象均可归纳为波,力学过程可归结为波群的运动,波函数是描写物质波振幅的函数。那么究竟什么是粒子?在他看来粒子不过是集中起来的波群,或者说粒子不过是SE的本征解、叠加而成的波包(wave packet)。N.Bohr对此作了批评,指出波包在传播过程中不断“发胖”导致了不稳定性,而粒子实际上却是稳定的。……不仅Schrödinger认识上的偏差得到了纠正,他对波函数的理解也欠深刻——德国物理学家Max Born提出了波函数的统计解释(statistical interpretation of wave functions),弥补了Schrödinger的缺憾,并因此获得了1954年Nobel物理学奖。我们知道Schrödinger获Nobel奖是在1933年,其时他46岁;Born获奖时是72岁,是一种迟到的承认和推崇。由于Born的工作,我们知道微观粒子不是经典粒子,对应的波不是经典波。为了强调这种区别,称用波函数描写的微观粒子状态为量子态。在电子双缝衍射实验中,尽管不能唯一地知道单个电子到达感光板的位置,但作为统计结果的衍射图形的唯一性是肯定的。因而在QM中是一种统计性的确定性(statistic definity),它有别于经典物理学中的Laplace-Newton式确定性。由此可知SE并不完全离开确定性,在具体应用中,无论波函数如何选取,物理问题的波函数必须保证物理结果的唯一性。某时某地出现粒子的几率是唯一的,从非相对论量子力学(NRQM)的角度看,粒子出现是必然事件,发生的几率应等于1,亦即
(38)
这是波函数归一化条件。无疑的,我们在写出上式时必定知道这指的是没有物质粒子产生或湮灭的物理过程。
在“光子是什么”一文中,笔者提出了如下观点[14]:“通常认为光子是电磁场量子,亦即电磁场经量子场处理后形成的方程可以描写光子。然而在物理思维上存在困难,例如很难了解光子物理形象的动力学。……光子形象仍然模糊不清;光波并不完全等同于传统电磁波,因为光子是微观粒子,波特性遵从统计规律,波函数表达几率波模式。然而现时却缺少光子几率波的方程。”对此,有人认为光子不是没有波函数,只是没有束缚态波函数:这才是光子和有质量粒子在波函数上的区别。有质量粒子,在场态下,具有束缚态波函数。光子和其它粒子,都有自由态波函数,就是平面波函数。光子是交换子,量子场论的理论模式下,光子不会再重复受到场本身作用,所以光子没有束缚态。
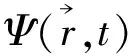
回过头来看“光子是什么”一文,它说“不能为光子写出波方程”(论据A),又说“现时缺少光子几率波的方程”(论据B)。A和B是不是一回事?先写出两个方程——经典的Maxwell电磁波方程和量子的Schrödinger波方程,前者为
(4a)
(39)
式中Ψ是几率波的波函数,m是粒子质量,U是势能函数。我们注意到,前者不包含任何与质量有关的元素。不过,我们在“光子是什么”一文中指出[14],有一种认为“光子有静止质量(m0≠0)”的理论,据此对Maxwell方程组作了修正,得到Proca方程组。对此这里不展开讨论,读者可参阅文献[14]。
不管怎么说,如从经典的Maxwell理论出发,电磁波的波方程与质量、动量概念都无关,也就谈不上“波粒二象性”的体现。Schrödinger方程则不同,它既是波动方程又在公式中有粒子质量(m)!这是很独特的,明显体现了粒子与波动的联系和结合。
光是电磁波的一种;光量子是一份份(分立的)电磁波能量的集中体现;但我们似乎不能把光子与电磁波等同——正是因为Maxwell电磁理论在解释光电效应时败下阵来,Einstein才在1905年提出“光由光子流组成”假说。既如此,不能认为有了公式(4a)就是“有了光子波方程”。正如1933年的Nobel物理奖的授奖词所说:“引进光量子以后,量子力学必须放弃因果关系的要求。……物理定律所表示的是某个事件出现的几率——我们的感官和仪器不完善,我们只能感觉到平均值,因此我们的物理定律所涉及的是几率”。……既如此,追求所谓“光子几率波方程”并不为错——但这样的方程现在并没有。如承认光子波动具有统计性,那么它与经典波动(如力学波、声波、电磁波)确实不一样。
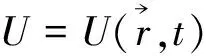

(40)
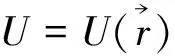
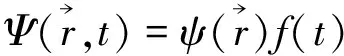
(41)
(42)
其模值平方为
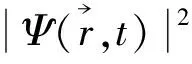
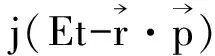
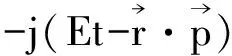
(43)
结果是一个与坐标无关的常数,表示在空间任何位置找到自由粒子的几率是一样的,亦即自由粒子的坐标位置完全不确定。可见,量子波动理论与测不准关系式有内在的一致性。这个概念也可以从另一角度解释——根据de Broglie关系式,我们有
(6a)
自由粒子即波长λ的单色平面波,它延展在整个空间(-∞ ~ +∞),根本没有确定的坐标。因此,波粒二象性与测不准关系式一致。
光子的非经典性还可由量子力学中全同粒子不可分辨性原理出发而看出。全同性原理导致两个同类粒子交换后波函数不变,有这种对称性的粒子是Bose子,如光子和介子,自旋为整数值,不必满足Pauli不相容原理。这些都是经典物理学不曾考虑过的问题。总之,波动性、粒子性其实都来自经典物理观念,但现在我们不能再用经典物理来研究光子。例如,虽然将辐射场用简谐振子来描写是波动图像,但它属于量子化了的波动而非经典的波动。总之,对光子的一些奇怪现象(如同态光子干涉、单光子同时通过双缝、量子后选择等),用传统上的经典性、确定性(determinism)都无法解释。
1958年P.Dirac[15]在其著作《Quantum Mechanics》中提出了“光子自干涉”的论断,认为单光子只能自己发生干涉,从来不会发生不同光子间的干涉。但实验表明不同激光器发出的光子可以相干,这也说成是“光子自干涉”就说不通了。为克服这一困难,应将“光子自干涉”理解为包括“同态光子干涉”在内。光子即使来自不同的激光器,只要进入同一量子状态,就是不可区分的全同粒子,就能发生相干,实验表明正是如此,20世纪60年代L.Mandel领导的弱光干涉实验对此做了许多研究。
但光子的怪异性质继续引起人们的注意。美国物理学家John Wheeler,在1979年提出一个思想实验,叫做延迟选择实验(delayed choice experiment)。它突显了量子理论与经典物理在实在性(reality)问题上的深刻分歧,集中展现出量子力学对传统实在性观念的挑战。1984年,C.Alley等人对这个思想作了实验室中的展示。Wheeler的设计如下:一个极弱的光源置于有一对平行狭缝的屏幕(S1)之前,该屏之后较远处放有屏幕(S2)。正如传统的T.Young实验一样,S2上面会产生干涉条纹,反映光波不同相位的影响。但是,如果进一步降低光源的辐射,以致一次只有一个光子通过S1,仍有干涉图案出现。如光子只通过一个狭缝,就难以解释。
现在于S1背后安装两个光子检测器(photon detectors),并且是每缝一个,以观察每个光子通过哪个狭缝。然而,每当实验者确定了光子的通道,干涉图形就不出现。这时实验者可以选择,或看光子朝向何处并破坏其波状行为,或选择不看并允许光子体现其波性,这就是归结为选择粒子或波动。光子可能两者都是,但不是在同一时间,某种程度上取决于实验者的选择……现在,又于S2背后安装两个观测镜(telescopes),也是每缝一个,以推断任一指定光子从哪个窄缝中显现出来。但是,这样做就破坏了干涉图形。因此,实验者的观测影响过去的自然界(光子呈现波性或粒子性)。这种怪现象被称为“量子的后选择”(quantum post-selection),表示观测者的选择能影响光子前期的行为。
Wheeler的“延迟选择”思想可改造为以下实验——减弱光源辐射使其只发出一个个光子,并且是在前一个光子打在S2上之后再发出后一个光子。S2先呈现随机性图形,但在光子增多后逐渐显出干涉条纹。对此,如认为将发出的光子与已达S2的光子发生干涉,即表示尚未发生的事件与已完成的事件互相作用,违反了因果律。故可认为每个光子都和自己干涉,而这只在光子同时通过双缝才能办到。一个粒子同时走两条路,在经典物理中是不可能的,说明光子具有奇异的性质。
总之,说“光子至今没有自己专属的波方程、波函数”,因而无法在科学的数学化意义上真实地代表和呈现光子的奇怪特性,这样讲是可以的。仅靠Maxwell波方程或平面波表达式非常不够,不能充分说明问题。我们在“光子是什么”一文中建议考虑走一条新路——尝试从Proca方程组入手,这有一定道理,虽然这样做要复杂许多。无论如何,怎样认识光子,甚至怎样认识电磁波,仍是有待解决的课题。……必须指出,正像人类习惯于认识宏观物质而不易理解微观粒子一样,人们通常容易接受具体可感知的波动的形象,例如水面波、声波、电磁波等,而对几率波就觉得不好接受和难于想像。但是,由于微观粒子的波动性取决于其统计性,波函数所代表的只是几率波,只有接受了这一概念才能理解原子内部的真实情形。
表2是笔者根据自己的论述形成的对电子、光子研究情况及理论思想的比较;很明显,与光子有关的事情并非已经都弄清楚了。

表2 电子和光子研究情况及理论思想的比较
6 光脉冲的负波速传播
波科学研究离不开对电磁脉冲(包括短波脉冲、微波脉冲、光频脉冲等)运动状况的理论分析和实验观测,在这两方面都有很大进展。在20世纪后期有一些重要成果,例如1970年C.Garrett和D.McCumber[16]首次在理论上提出利用具有正或负吸收线的媒质实现反常色散,完成群速超光速传播,甚至负群速传播。其文中指出利用Gauss脉冲这种前沿和后沿平滑的光脉冲,当光脉冲的中心频率在媒质板吸收线附近时,会出现反常色散现象。此时如果媒质板较薄,出现的脉冲功率谱基本上仍然是Gauss型的,即基本不失真。脉冲的峰值的出现甚至可能早于输入脉冲进入板子的时刻,也就是实现负群速传播。而对于较厚的板子可以利用数值技术进行分析,只要光脉冲宽度比原子线窄,一般不会出现严重失真;只有当总增益和总衰减都极大时才会出现严重失真。
Garrett首先给出在脉冲宽度远小于原子线宽度时,脉冲表达式
(44)
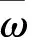
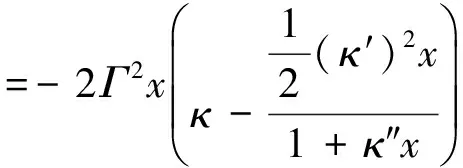
(45)
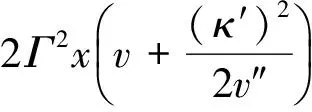
(46)
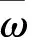
(47)
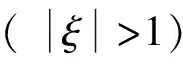
Garrett文章首次为群速超光速和负群速实验提供了理论基础;在光谱增益线或吸收线上形成下陷时,即光谱烧孔效应时,就会使输入脉冲峰进入媒质前,就在出口处观测到输出脉冲峰,也就是负群速的现象;并且首次指出这个现象并不违背因果律。
虽然1907年Einstein[17]讨论了负速度和负时间,1914年Sommerfeld[18]和Brillouin[19]讨论了负群速,但直到1982年都没有人做过实验。当群速由0逐步增大,一直到无限大(vg=0~∞),然后转为负群速(vg<0),因而负群速是比无限大群速“还要大”的速度,这样的表述是SB理论认同的。然而在实际上有没有负群速?Sommerfeld和Brillouin不知道,Garrett其实也不知道。
1982年S.Chu和S.Wong[20]发表论文“吸收媒质中的线性脉冲传播”,似为用实验证明负群速存在的第一人,是负速度在实验上取得了突破。假定受实验样品厚度为L,群时延为τg,则群速为
(48)

图1 Chu和Wong群速实验装置示意图
故测出τg即可算出vg。S.Chu和S.Wong的实验系统见图1,实验使用具有3平板双折射滤波器的染色泵浦激光器,激光器被调节到可以很好的隔离534nm激子线的边界附近,通过厚度分别为0.12mm、0.5mm、和2.0mm的非涂层内腔式标准具来改变激光器的频带宽度。0.5mm和2.0mm的标准具分别产生22ps和48ps的脉冲。外延层的厚度在9.5μm到76μm调整使吸收峰值不超过6个吸收长度。最后通过放入和移出样品确定非谐振脉冲的传输速度c/n0,n0为非谐振折射率。测试结果如图2;在图2中实线是群时延的预期值,虚线为吸收系数,方块是22ps脉冲时的测量值,圆圈是48ps脉冲时的测量值。
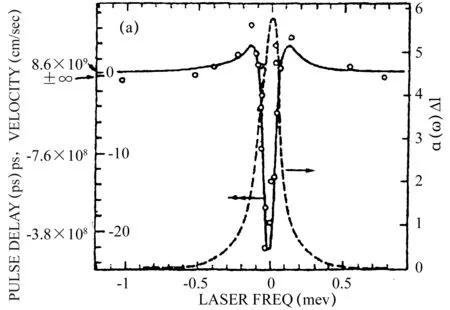
(a)氮浓度1.5×1017cm-3、外延层厚度76μm
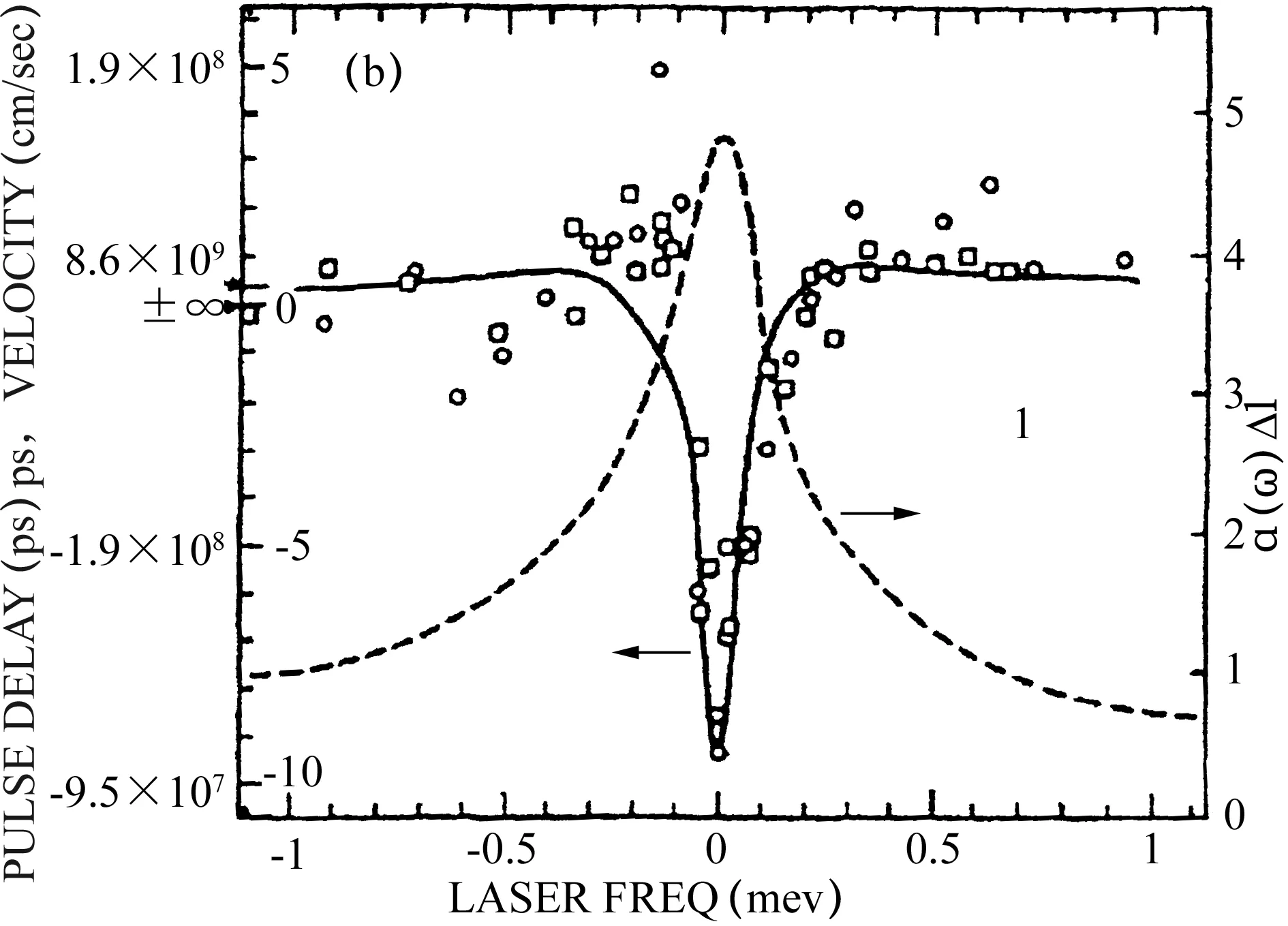
(b)氮浓度3.8×1018cm-3、延层厚度9.5μm图2 群时延曲线和吸收谱
图1和图2,以及之前的Garrett理论,都有基本的重要性——无论对回溯科学发展史及指导当前的现实研究均是如此。因为这是我们了解到的第一个负群速的理论和实验,为之后的研究和实验提供了参考和基础。回想在2000年,当WKD实验报告在《Nature》刊出后,为了这个“脉冲峰在进入气室(cell)就已经离开了气室”,国内外物理界都曾争论不休。但在2000年的很多年前就由Garrett等仔细分析讨论过,由Chu等测量研究过,根本不必大惊小怪。
前已述及,WKD实验中时间差Δt为负(Δt=-62ns),故物理表现为光脉冲超前,而(-Δt)为提前时间。因而WKD论文说[13]:“这意味着通过原子气室传播的光脉冲峰在进入气室前就已经离开了气室”。并且最重要的是脉冲波形没有发生变形,这是WKD实验的出色之处。图3是WKD实验装置示意图。在这里我们强调指出,从Garrett(1970年)到Chu(1982年)再到WKD(2000年),研究结果都是“peak of the pulse appears to leave the cell or the sample before entering it。”
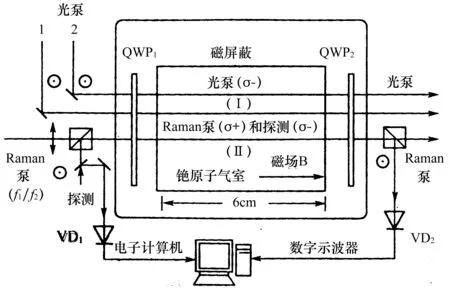
图3 WKD实验(王力军小组超光速实验)的布置
2012年美国NIST的R.Glasser[21]通过四波混频技术,在种子脉冲频率和产生的共轭脉冲频率的增益线和吸收线上产生的不对称的下陷,形成反常色散。在降低实验设置的复杂度同时,使输入种子脉冲和生成的共轭脉冲都实现了负群速传播,而且其中共轭脉冲传播的更快。测量到(-50ns)的时延,获得(-c/880)的负群速。而且实验中通过控制输入种子脉冲的频率失谐和功率来控制输入种子脉冲和生成的共轭脉冲的群速,不仅可以使种子脉冲和共轭脉冲获得负群速,还可以控制脉冲的波形,使得在波形失真最小的情况下实现负群速传播。
我们团队在2014年做成功一项负群速实验[22],其方法有独特之处。方案的要点是使用左手传输线(LHTL),并使用互补类Ω结构(complementary omega-like structures,COLS)构成缺陷地板微带左手传输线,通过这种互补结构的缝隙/条带实现负介电常数/负磁导率。对于整体COLS来讲互补类Ω结构相当于在原有的传输线中并联上电感,是实现负磁导率的关键,互补类Ω结构间和微带线的作用相当于加入串联的电容,是实现负介电常数的关键。
我们调整COLS结构中不同的参数,以获得反常色散。通过多次调整,发现当COLS结构的尺寸较小时,反常色散现象强烈,此时群时延更超前。但这时反常色散的频带会非常窄。然而相反当COLS的尺寸较大时,反常色散的现象减弱,群时延超前少,但此时反常色散的频带会变宽。经过反复计算和试验选择好参数,最终所用样品长度为L=60mm。得到的结果是,电磁脉冲通过样品的时间,即负群延时为τg=(-0.062ns)~(-1.540ns)。由vg=L/τg得到vg=(-0.13c)~(-1.85c)。我们观测到了时间超前的输出波形,见图4;它是数字示波器显示的载波频率5.94GHz时的波形图,因此是在微波(厘米波)实现了矩形阶跃脉冲经过样品的负群速传播。
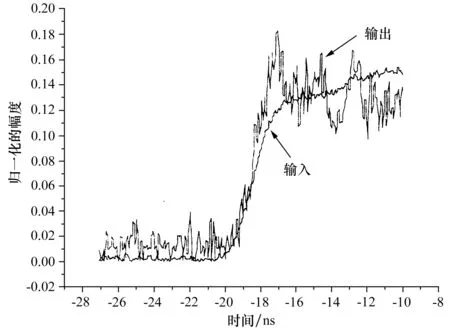
图4 本文作者在实验中得到的NGV波形显示
本节举出的几个负群速实验,都是通过测量负的群时延,也就是时间上的超前。这种负的群时延似乎和我们的生活经验相矛盾,但这只是一种时间的对称性,并不能使我们回到过去,这种时间上的超前也不违反因果性。自上世纪后期至今,众多实验中测得的隧穿时间甚至小于粒子以光速在真空中穿过相同的距离所需的时间。由于这些实验结果看似违背了因果律,“惊慌物理学家们”提出脉冲重组的假说,认为在隧穿过程中透射波包并不是由入射波包转化的,而仅仅由最前端的部分组成。但这对于入射光脉冲是Gauss脉冲和正弦调制波或许可以说的通;但是对于一些使用矩形脉冲和阶跃脉冲的实验似乎有些说不通;这也包括我们的实验,因为这种情况下观测的是脉冲上升沿的部分。……脉冲重组一词的英文是reshaping,前面也称为脉冲整形。
一直以来,有一种观点强调出射脉冲是入射脉冲前沿造成的,不是其峰值所造成。这一说法最先也是来自Garrett:“输入脉冲峰进入前就离开的输出脉冲峰是由输入脉冲前沿的分量们形成的,而非来自输入脉冲峰的分量们”……甚至到2001年这说法仍被人重复;有文章说:“WKD实验中出射光脉冲虽然是在入射脉冲峰进入媒质前出现的,但此前入射脉冲前沿早己进入媒质:故出射脉冲可看作是入射脉冲前沿与媒质相互作用产生的。” 很明显,作为这一观点倡导者的Garrett,就是一位“惊慌的物理学家”;一方面他做出了贡献,但仍缺少洞穿自然的目光,未能在认识上抵达事物的本质。更深刻的理解要求思考什么是过去,什么是未来;而负时间、负速度又意味着什么。……关于这方面的论述,可参阅黄志洵的文章[23、24]。
7 Bose双三棱镜中的消失波
消失态是电磁环境中的一种常见的状态,基本特征是场强自原生地向远处按指数规律下降。电磁波通过电抗性突出的媒质是有普遍意义的情况,它对应导波模式、色散媒质、电离气体中的波传播问题。1897年,Rayleigh[25]在分析金属壁矩形波导时最早预言了消失态传播。为了分析截止波导,看来可以把消失态当作具有虚波矢(虚波数)的状态;并且可将其看成驻波,场变化在各处同时发生,故在传播方向上无相移。
在量子力学中,势垒内的消失态也具有虚数的波参量;这时可用Schrödinger方程而作出说明,它可类比经典电磁理论中的Helmholtz方程。实际上量子隧穿是常见的物理过程,可在许多场合观察到;例如Bose[26]的双三棱镜实验现象,这个发现也是在1897年;当时,在英国工作的印度科学家J.Bose用厘米波波长的电磁波作用于两个相对的三棱镜时的情况来演示经典电磁领域的隧道效应现象。图5是引自原文的示意,(a)表示波的通过和反射,(b)表示实验装置;L是提供入射波束的信号源,P、P′是两个等边三角形的棱镜;圆盘是可旋转的(为了改变入射角),而A、B是接收器的两个不同位置。
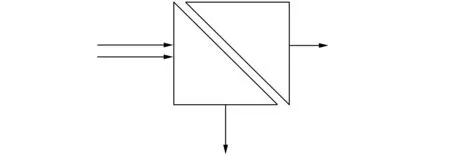
(a)
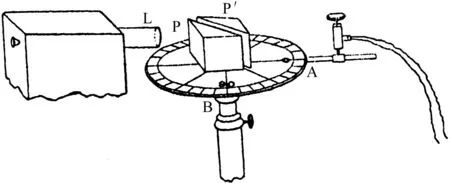
(b)图5 Bose实验的基本装置

图6 两块平板玻璃中间有空气隙的情况
现在我们用图6说明Bose实验的原理;取两个玻璃板平行相对,中间有等宽(宽度d)的空气隙。如光束自左方斜向入射(与法线夹角θ),则在气隙左方的玻璃(I区)内形成电磁波(光波)从n>1区(光密媒质)向n≅1区(光疏媒质)的传播,界面上多数光波反射,少数光波将隧穿通过气隙(区域Ⅱ),而进入另一光密媒质Ⅲ区。虽然波包向玻璃板长度方向传播,与玻璃板垂直的z向却发生隧穿过程(tunneling process)。当然入射角θ应大于总内反射临界角,即
θ>θc=sin-1(1/n)
(49)
上式中n为玻璃的折射率。当距离小于波长时,Bose发现在右方玻璃板中确有波通过了气隙而在Ⅲ区内传播。这是最早的隧道效应实验,也是最早的消失波实验。当然,从1897年算起要过30年才有量子力学(QM)的发明,Bose本人在1897年也不知道这是一种量子隧道效应。所以,我们看到了经典电磁理论与量子理论互相沟通的例子。
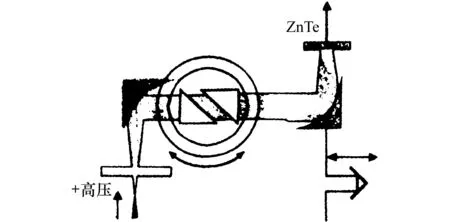
图7 太赫波段的全反射超光速实验装置
Bose的实验表明,当入射波被全反射时,有少数波穿越气隙d进入另一棱镜,亦即发生全反射时在光疏介质中会发生消失波。1949年,A.Sommerfeld最先指出可以用QM解释Bose实验,在气隙中发生的物理过程对应量子势垒中的消失波衰减过程。此后,2000年J.Carey[27]用太赫波重做双棱镜实验,发现了超光速现象。图7是他所用的实验装置;THz发生器使用GaAs晶体加2000V偏压,得到THz的脉冲脉宽为0.85ps、波长1mm。双棱镜设在一个平移台上,使两棱镜间的距离d可以变化。棱镜的材料是Teflon,n=1.43,故全反射临界角为44.4°。消失波与非消失波的光路见图8。Carey取d=0~20mm,入射角θ=35°~55°,做了一系列实验。结果是脉冲重心时延和群时延均可以为负值,是超光速传输的证明。Carey说,如信号以接近并稍大于临界角的入射角入射,信号可以基本上无衰减地作超光速传播。但这要求光信号严格准直,棱镜为无限大。他认为“以全反射实现超光速信息传输是可能的”,但d足够大时信号主要是非消失波,其脉冲重心速度(在气隙中)为0.99c,是亚光速。
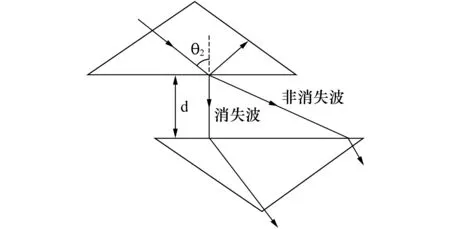
图8 Carey双棱镜实验示意
在双三棱镜的气隙中,消失态有以下方程:
A=αd (Np)
(50)
式中A为衰减量,α衰减常数;上式表示场幅按照e-αd的规律衰减。重要的是这个规律已有实验上的证明;2001年的Haibel和Nimtz实验,用n=1.6的材料做成双三棱镜,故总内反射临界角为θc=sin-1(1/n)=38.5°;现如按θ=45°入射,则会造成Bose效应。在微波使用两个频率(f1=9.72GHz,f2=8.345GHz),得到A~d关系的实验曲线如图9;对应的α测量值为:α1=0.93dB/mm,α2=0.73dB/mm。Nimtz说,这结果与下式的计算值是一致的:
(51)
笔者认为这工作可能是对Bose效应的首次实验证明。
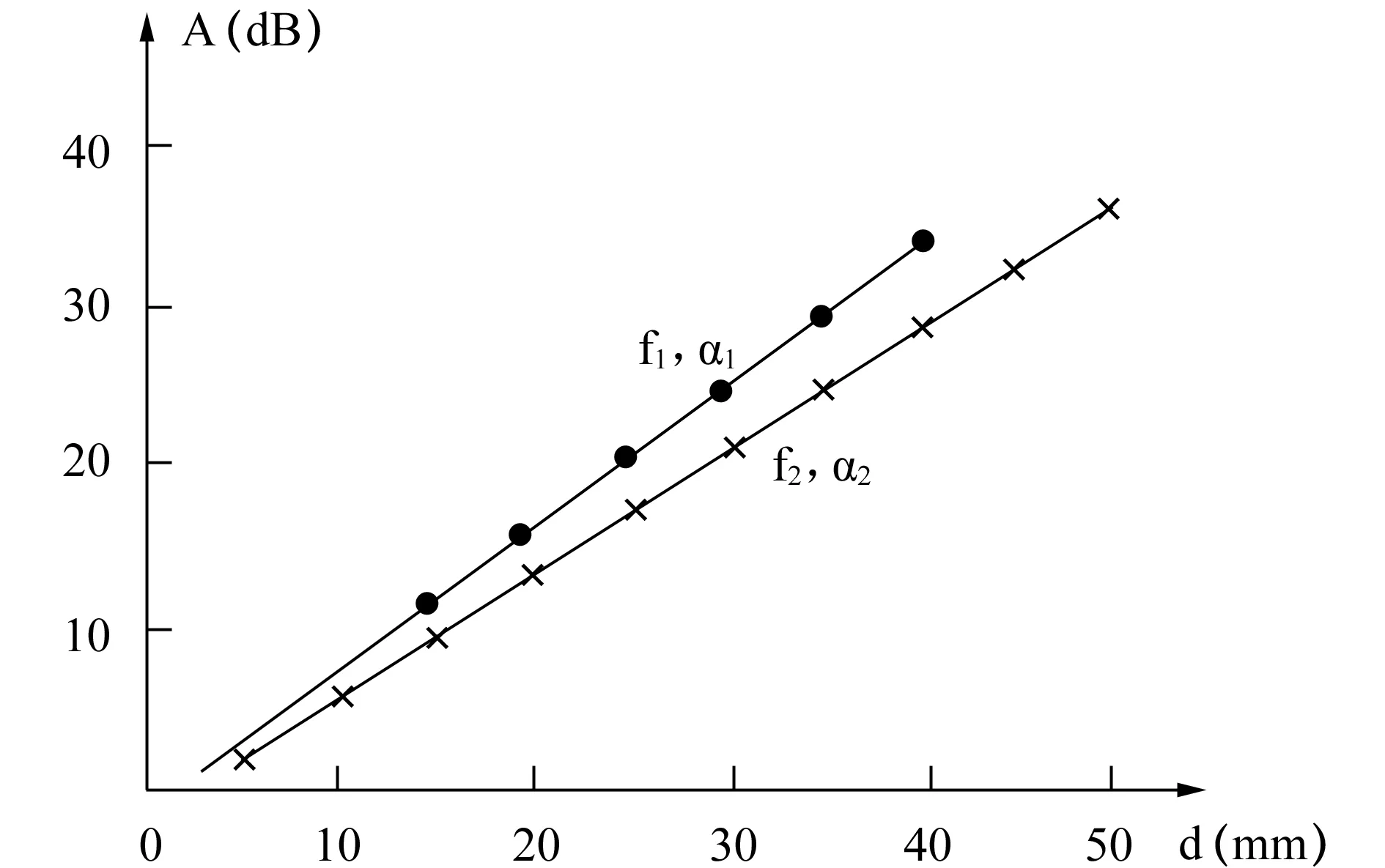
图9 双三棱镜气隙中的衰减常数
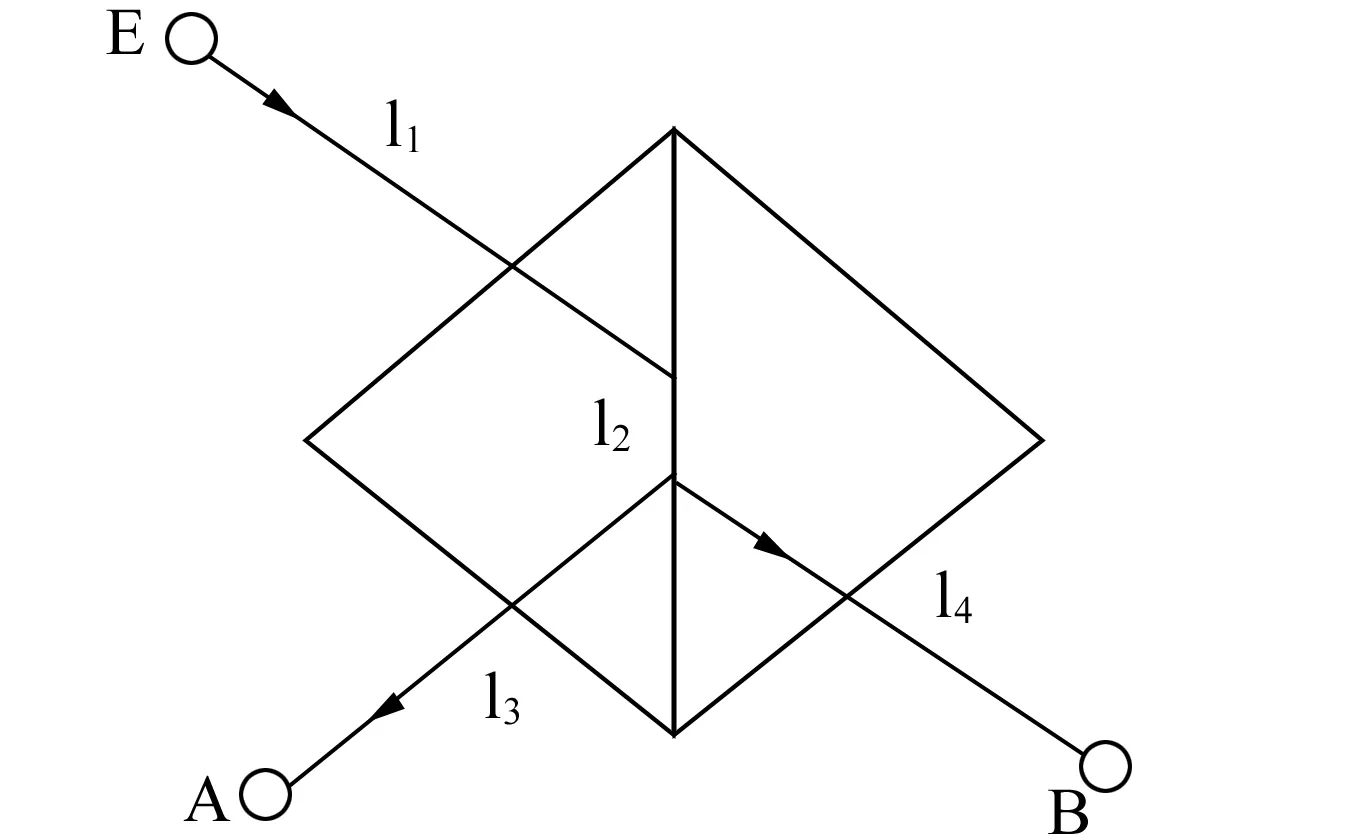
2006~2007年,Nimtz公布了他用双三棱镜做超光速实验的情况[8,28]。他们说:“光学中的消失模对应量子电动力学(QED)创始人Feynman引入的虚粒子(virtual particles),这种模式的典型例子是双三棱镜的受抑全内反射(FTIR)。我们企图用米级宏观尺度来证明消失模的QM行为,由于零相移通过势垒的传播似不需要时间”。他们采用折射率n=1.6的塑胶有机材料构成双三棱镜,信号频率9.15GHz(波长3.28cm);三棱镜尺寸为40×40cm2,反射临界角为38.7°。采用盘形天线(直径35cm),接收天线与棱镜表面平行,并可移动;微波是TM模式。实验结果是:反射信号和透射(隧穿)信号在同一时刻被接收到(时延均为100ps)。由于反射光束和透射光束的路程相同,而透射光束可能多穿过长度为d的区域就像是不用时间的传播。他们说,虽然这是对狭义相对论(SR)的违反,但可用QM和QED作描述和解释。
(a)
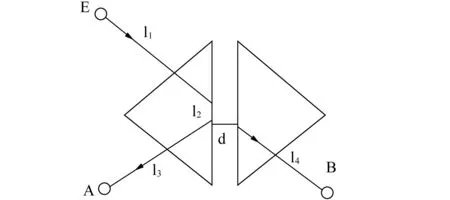
(b)图10 对“双三棱镜超光速实验”的说明
现根据图10叙述实验方法和过程——使用两块玻璃棱镜,拼起来是每边40cm的立方体。使用波长较长的微波(λ≅33cm);对大隧穿距离而言λ足够长,对光子路径可被棱镜拐弯而言λ足够短。实验时使微波束从第一个三棱镜面的右方斜向射入(θ>θc),在镜内底面被反射后由另一斜面射出,到达检测器A。根据Bose-QTE效应,有少数波束穿过底面,并通过间隙d从第二个三棱镜的底面进入该棱镜,再折射出去到达检测器B。由于A、B的位置对称安放,在d=0时两个光路的长度相同。但当d≠0,后一光路较长,增量为d。现在的实验发现两个光路的信号传输时间没有差别,或者说两路微波到达A、B的时间相同。故可判断后一情况的波速较快,或者说微波穿过间隙(亦即势垒)没有耗费时间,即速度为无限大(即便v≠∞,也可断定v>c,而且大出很多)。对图10(a)有:
(52)
式中v1、t1分别为由E到B的速度和时间,l2是Goss-Hänchen位移造成的(夸大画出);对图10(b)有:
(53)
如实验发现t1=t2=τ,则有:
(54)
故v2>v1;若v1是光速,则有
(55)
故v2>c,亦即发现了超光速。此外,实验还发现当拉开棱镜时(即逐步加大d),隧穿时间不变;但在d≥lm时就无法观察了。……考虑到Carey的实验,我们可以说“从太赫波到微波都以双三棱镜实现了超光速的波传播”。
Nimtz团队的实验早已被媒体所报道,例如2007年8月27日德新社发出电讯称:“两名德国物理学家宣称已做到了不可能的事——打破光速”;8月28日中国的《参考消息》报译载了德新社的电稿,所用标题为“德发现打破光速现象”。……Günter Nimtz教授与我相熟,我们多次交换彼此的科学著作;他在quantum tunneling这一研究方法上坚持不懈,令人佩服;笔者当时曾致电祝贺。2016年11月10日,Nimtz发来邮件,提到他过去曾用实验发现在隧穿中的现象——以零时间实现超光速能量传送(见:PRE,1993,Vol.48,632;Found Phys,2014,Vol.44,678)。
8 引力波存在性问题
虽然本文主要讨论经典波动中的电磁波和量子波动,却不能回避所谓“引力波”的问题,因为这已被媒体炒热;而且据说中国的一些科研机构纷纷准备上马[29],正等待政府高层审批。对于2016年2月美国LIGO(激光干涉引力波天文台)宣布“发现了引力波”[30],国内外已有众多反对的文献发表[31-37];当然也有赞成和支持的[29]。在这里我们仅从理论上作些分析。
引力在中国也称为万有引力,英文是gravity;它是Newton发现的。引力的本质是什么?Newton没有回答,他只给出与引力有关的规律——万有引力定律(也叫平方反比定律[4])。Newton说:“迄今为止我还不能从现象中找出引力特性的原因,我也不构造假说”。(着重点为笔者所加)。在Newton时代并没有“引力场”的说法,这是由于后来电磁学迅猛发展,电磁场(electromagnetic field)的存在已经证实,人们研究时就创造了gravitational field这个词。……笔者的学术观点是,承认引力场存在,却不承认有引力波(gravitational waves)。也就是说,不但要分析LIGO在技术(设计和实验)上的问题,更重要的是在理论层面弄清楚“寻找引力波”的动力来源是否正确。由于Newton万有引力定律与Coulomb电荷力定律的相似:
(56)
(57)
这两者都是平方反比定律(inverse squares law,ISL),两者都是静态场(static fields)。因此,万有引力是无旋场。静电无旋场由极性的(正或负)电荷所产生,引力无旋场由中性粒子或物体的质量所产生。静态场(包括静电场)的根本特点是无旋场(电场矢量、磁场矢量的旋度为零)。这一点是重要的,因为电磁场的波方程(wave equation,也称波动方程)的推导是由对普遍形式的Maxwell方程的等式两边取旋度而开始的,从而得出空间有源时的波方程。对于静态场,以上讨论都不存在,亦即即使有(电磁)场也没有(电磁)波。总之,交变场才产生电磁波,静态场不产生电磁波。因此构成并行的理论体系——有电磁波存在的交变场理论,无电磁波存在的静态场理论。
引力场既然是无旋的静态场,从根本上就缺乏产生“引力波”的基础。相对论者说,Einstein理论(相对论力学)中,引力不再是一种力,而是可弯曲时空的几何效应。但这样讲也不能证明引力场是旋量场,又如何能证明引力波一定存在呢?……总之,必须强调指出在场论中存在两大类的区分(旋量场、无旋场)是根本性的基础理论。
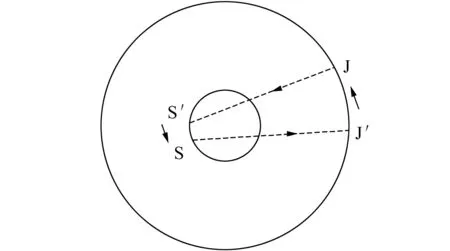
图11 讨论引力速度的示意图S—太阳;J—木星。
1998年T.Flandern[39]指出,对太阳(S)—地球(E)体系而言,如果太阳产生的引力是以光速向外传播,那么当引力走过日地间距而到达地球时,后者已前移了与8.3min相应的距离。这样一来,太阳对地球的吸引同地球时太阳的吸引就不在同一条直线上了。这些错行力(misaligned forces)的效应是使得绕太阳运行的星体轨道半径增大,在1200年内地球对太阳的距离将加倍。但在实际上,地球轨道是稳定的;故可断定“引力传播速度远大于光速”。他的计算结果是vG=(109~2×1010)c。2016年9月22日,朱寅在《Research Gate》上发表文章,题为“The speed of gravity: an observation on galaxy motions”,根据分析得出引力速度vG>25ly/s(ly是光年)。由于1ly=9.5×1012km,可以算出这相当vG>7.92×108c。
近年来开展了Coulomb场传播速度研究;例如2014年R.Sangro[40]指出:和引力场传播速度一样,Coulomb力场传播速度远大于光速。这是不奇怪的,我们已指出引力场与静电场相似。但相对论力学不承认引力传播速度远大于光速,因为狭义相对论(SR)已确定了光速c是宇宙中的最高速度。为了维护自身理论体系一致性,国内外相对论者坚持说引力以光速传播”[29];但这并非事实。文献[29]认为,引力场方程在弱场、线性条件下,并按谐和条件分析时,可以把解写为
(58)
并说,由于这是一个推迟解,(t-r/c)项即表明情况和电磁理论中一样,“证明引力场以光速(c)传播”。我们认为这是荒唐的,因为引力作用中会有自己的常数,凭什么把光速c强行引入?引力本身与光、与电磁场没有关系,这是明明白白的事。形式化地搞一点推迟势(retarded potential),不能证明引力场以光速传播;何况D′Alembert方程和推迟势概念方法也是从电磁场那里“学”(实际上是“抄”)来的。由于电磁场和电磁波的理论与实践取得了历史性的伟大成就,研究引力时作些借鉴可以理解。但把电磁学的概念和方法机械地、形式主义地照搬,那就错了。……不过引力这个题目太大,更多的讨论请见笔者的2015年文章[41]。
9 结束语
波科学本身博大精深,不可能详细讨论。它取得了很大的成绩,但在许多问题上又显得支离破碎、互相矛盾。改进的希望在于以现代数学作支持的现代电磁理论和量子理论,以及设计巧妙的专题实验。对于国内外的有关研究工作,我们坚持从科学视角进行评价,并力求客观而公正。当然我们也坚持提出独立的新观点,因为这是科学研究工作者的基本权利。
[1]Schrödinger E. Quantisation as a problem of proper values[J]. Ann d Phys,1926,79(4):1-9.(又见:Schrödinger E. Lectures of Schrödinger.中译本:范岱年、胡新和译,薛定谔讲演录[M].北京:北京大学出版社,2007.)
[2]黄志洵.波动力学的发展[J]. 中国传媒大学学报(自然科学版),2008,15(4):l~16.
[3]黄志洵.波科学的数理逻辑[M]. 北京:中国计量出版社,2011.(又见:黄志洵.波科学与超光速物理[M].北京:国防工业出版社,2014.)
[4]Newton I.Philosophiae naturalis principia mathematica[M].London:Roy Soc,1687.(中译:牛顿.自然哲学之数学原理[M].王克迪译.西安:陕西人民出版社,2001.)
[5]罗俊. 牛顿反平方定律及其实验检验. 见:10000个科学难题(物理学卷)[M].北京:科学出版社,2009.
[6]Kline M.Mathematical thought from ancient to modern times[M].New York:Oxford Univ Press,1972.
[7]Maxwell J. A dynamic theory of electromagnetic fields[J]. Phil Trans,1865,(155):459~512.
[8]黄志洵. 论消失态[J].中国传媒大学学报(自然科学版),2008,15(3):l~9.
[9]Steinberg A,Kwait P,Chaio R. Measurement of the single photon tunneling time[J].Phys Rev Lett,1993,71(5):708~711.
[10]宋文淼、阴和俊、张晓娟. 实物与暗物的数理逻辑[M].北京:科学出版社,2006.(又见:宋文淼. 矢量偏微分算子[M].北京:科学出版社,1999.)
[11]黄志洵. 负波速研究进展[J].前沿科学,2012,6(4):46~66.
[12]黄志洵. 波粒二象性理论与波速问题探讨[J].中国传媒大学学报(自然科学版),2014,21(2):9~24.
[13]Wang L J. Kuzmich A,Dogariu A. Gain-asisted superluminal light propagation[J].Nature,2000,406:277~279.
[14]黄志洵. 光子是什么[J]. 前沿科学,2016,10(3):75~96.
[15]Dirac P A M. Quantum Mechanics[M].London:McGraw Hill,1958.
[16]Garrett C,McCumber D.Propagation of a Gaussian light pulse through an anomalous dispersion medium[J].Phys Rev A,1970,1(2):305~313.
[17]Einstein A.The relativity principle and it’s conclusion[J].Jahr der Radioaktivität und Elektronik,1907,4:411~462.(中译:关于相对性原理和由此得出的结果[A].范岱年,赵中立,许良英译.爱因斯坦文集[M].北京:商务印书馆,1983,150~209.)
[18]Sommerfeld A. Uber die fortpflanzung des lichtes in dispergierenden Medien[J],Ann d Phys,914,44(1):177~182.
[19]Brillouin L. Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys,1914,44(1):203~208.
[20]Chu S,Wong S.Linear pulse propagation in an absorbing medium[J].Phys Rev Lett,1982,48 (11):738~741.
[21]Glasser R,et al.Stimulated generation of superluminal light pulses via four-wave mixing[J]. Phys Rev Lett,2012,108: 17~26.
[22]Jiang R(姜荣),Huang Z X(黄志洵),Miao J Y(缪京元),Liu X M(刘欣萌).Negative group velocity pulse propagation through a left-handed transmission line[J]. arXiv.ore/abs/1502. 04716,2014.
[23]黄志洵. 超光速物理学研究的若干问题[J].中国传媒大学学报(自然科学版),2013,20(6):1~19.
[24]黄志洵. 量子隧穿时间与脉冲传播时间的负时延[J]. 前沿科学,2014,8(1):63~79.
[25]Lord Rayleigh.On the passage of electric wave through tubes,or the vibrations of dielectric cylinders.[J] Philos Mag,1897,43(261):125~132.
[26]Bose J. On the influence of the thickness of air-space on total reflection of electric radiation[J]. Proc Roy Soc(London),1897(Nov): 300~310.
[27]Carey J J.Noncausal time response in frustrated total internal reflection[J].Phys Rev Lett,2000,84,1431~1434.
[28]Haibel A,Nimtz G.Universal relationship of time and frequency in photonic tunneling[J]. Ann d Phys,2001,10:707~712.
[29]赵峥,刘文彪,张轩中. 引力波与广义相对论[J].大学物理,2016,35(10):1~10.
[30]Abbott B P,et.al. Observation of gravitational wave from a binary black hole merger[J] . Phys Rev Lett,2016,116:06112 1~16.
[31]梅晓春,俞平.LIGO真的探测到引力波了吗?[J]. 前沿科学,2016,10(1):79~89.
[32]黄志洵,姜荣. 试评LIGO引力波实验[J].中国传媒大学学报(自然科学版),2016,23(3):1~11.
[33]Mei X,Huang Z,Ulianov P,Yu P. LIGO experiments cannot detect gravitational waves by using laser Michelson interferometers[J]. Jour Mod Phys,2016,(7): 1749~1761.
[34]梅晓春,黄志洵,P.Ulianov,俞平.LIGO实验采用迈克逊干涉仪不可能探测到引力波[J].中国传媒大学学报(自然科学版),2016,23(5):1~7.
[35]Ulianov P,Mei X,Yu P. Was LIGO’s gravitational wave detection a false alarm? [J].Jour Mod Phys,2016,(7): 1845~1865.
[36]Engelhardt W. Open letter to the Nobel Committee for Physics. DOL: 10.13140/RG 2.1.4872.8567,Dataset June 2016,Retrieved 24 Sep 2016.
[37]黄志洵. 再评LIGO引力波实验[J].中国传媒大学学报(自然科学版),2016,23(5):8~13.
[38]Eddington A.Space,time and gravitation[M].Cambridge:Cambridge Univ Press,1920.
[39]Flandem T.The speed of gravity:what the experiments say[J].Phys Lett,1998,A250:1~11.
[40]Sangro R,et al.Measuring propagation speed of Coulomb fields[J].arXiv:1211,2913,v2[gr-qc],10 Nov 2014.
[41]黄志洵.引力理论和引力速度测量[J].中国传媒大学学报(自然科学版),2015,22(6):1~20.
(责任编辑:龙学锋)
The Improvements of the Wave Sciences Theory
HUANG Zhi-xun1,JIANG Rong2
(1.Communication University of China,Beijing 100024;2.Zhejiang University of Media and Communication,Hangzhou 310018)
Wave is a form of material existence,but also a unique form of material movement.Wave science studies classical waves and quantum waves,and these two can not be separated.For example,electromagnetic waves are not only the classical wave of the macrocosm,but also the waves associated with the microscopic world.That is reflected in the photon,which is a unique microscopic particle.In 1926,Schrödinger created the quantum wave mechanics,and the Schrödinger equation became the basic equation that reflected the laws of motion in the quantum world.The complexity of the wave function in quantum mechanics comes from the complexity of the nonclassical wave.Photons are generally considered to be electromagnetic field quantaes,but photons should not be equated with electromagnetic waves.Such as the photon is also like electrons(wave nature has statistical properties),and the photon is not exactly the same as the classic electromagnetic wave,so discussed“photon probability wave equation problem”is not wrong.So it is said that that photons have not their own proprietary wave function and wave equation,therefore photon strange properties can not be accurately represented and presented.An important content of the wave science is the self-consistent mathematical logic structure of electromagnetic wave.To this end,a mathematical method different from the classical mechanics(CM) was used,such as theory of vector operator and theory of generalized function. Newton’s classical mechanics and Einstein’s relativity mechanics are mainly for particles or objects,but the field and the wave is not a substance material.The method of operator operation and the concept of wave function space in quantum mechanics(QM) have great significance to the study of wave science,while modern electromagnetic field theory is very suitable for the analysis of wave science,can provide the basic vector equations of electromagnetic waves,and conspicuously separates curl field and non-curl fields.The study of wave velocity is a key point and breakthrough in the exploration of wave science. Although the research of wave science can not be separated from classical mechanics,it can not follow CM’s way of thinking,and the scalar nature of wave velocity proves that.In this paper,the group velocity formula in wave science is re-deduced and re-proved.The WKD negative group velocity experiment published in 2000 was not“a mistake in the formula”.…Theoretical and experimental research on the propagation of negative wave velocity of light pulses since 1970 are still very instructive in today,because that is related to the understanding of “negative time” and “advanced waves”.The related research and the research of evanescent wave in Bose double prism have enriched the content of wave science,and improved the understanding of that.Finally,on February 2016,the US LIGO announced that the gravitational waves were found,and multinational scientists(Germany,Brazil,China,etc.) think that the results are questionable. They have published papers in scientific journals,or sent a letter to Prof.Olle Inganäs,who is the Chair of the NOBEL Committee for Physics,for making a sharp criticism of LIGO.However,in this paper it’s pointed that there are two different aspects of the problem of “finding LIGO gravitational waves”——that may be LIGO’s technical level is not enough,or may be that their method is based on the wrong theory? In this paper,it's accounted that there is a fundamental point in the field theory,which is that the field is divided into two categories——curl fields and non-curl fields,while gravitational force found by Newton and Coulomb electrostatic field are all non-curl fields,So it's lack of foundation for the existence of gravitational waves.It has been asserted that “gravitational force propagation at the speed of light” is an erroneous statement that is not in accordance with the facts.The gravitational field propagates at the speed which is far faster than the speed of light,but it is not the action at a distance with infinite speed.It’s a useful inspiration that the Coulomb electrostatic field propagation at superluminal speed has been recently found.
wave sciences;wave mechanics;classical waves;quantum waves;electromagnetic waves;gravitational waves;photons
2016-11-25
黄志洵(1936-),男(汉族),北京市人;中国传媒大学教授、博士生导师,中国科学院电子学研究所客座研究员, E-mail:huangzhixun75@163.com.
TN911.72
A
1673-4793(2016)06-0001-22
改进波科学理论的一个重要内容是电磁波自洽的数学逻辑结构,为此要使用与经典力学(CM)中不同的数学方法,例如矢量算子理论和广义函数论。Newton的经典力学和Einstein的相对论力学主要针对实物(粒子或物体)而建立,但场与波并非实体物质。量子力学(QM)中的算子运算方法和波函数空间概念对波科学研究有重要意义,而现代电磁场理论非常适合波科学分析,能提供基本的电磁波矢量方程组,并突出地把旋量场、无旋场区分开来。
波速研究是波科学探索的一个重点和突破口,尽管波科学研究不能脱离经典力学,但不能完全沿用CM的思维方式,波速的标量性就是证明。本文对波科学中群速公式的重新推导表明,2000年公布的WKD负群速实验并非“在计算公式上犯了错误”。……自1970年以来科学界开展的对“光脉冲负波速传播”的理论与实验研究,在今天仍深具启发性,因它关系到对“负时间”和“超前波”的理解。相关的研究以及对Bose双三棱镜中的消失态研究,丰富了波科学的内容,并改进了对它的认识。
最后,关于2016年2月美国LIGO宣布的“发现了引力波”,已有多国(德国、巴西、中国等)的科学家认为其结果可疑。他们或在科学刊物上发表论文,或致函NOBEL物理学奖委员会主席Olle Inganäs教授,对LIGO提出了尖锐的批评。然而本文指出,对“LIGO发现了引力波”一事有两个不同层面的问题存在——是LIGO的技术水平不够,还是其方法依据的理论有问题?本文认为在场论中有一个根本点是把场分为两大类——旋量场和无旋场,而Newton发现的万有引力和Coulomb静电场一样都是无旋场,因此缺乏存在引力波的基础。有人至今断言“引力以光速传播”,是与事实不符的错误说法。引力场以远大于光速的速度传播,但不是无限大速度的超距作用。不久前发现的“Coulomb静电场以超光速传播”是有益的启示。

