吸气式超声速导弹弹道优化设计与分析①

明 超, 孙瑞胜, 梁 卓, 白宏阳

(1.南京理工大学 能源与动力工程学院, 南京 210094;2.中国运载火箭技术研究院,北京 100076)

吸气式超声速导弹弹道优化设计与分析①

明 超1, 孙瑞胜1, 梁 卓2, 白宏阳1

(1.南京理工大学 能源与动力工程学院, 南京 210094;2.中国运载火箭技术研究院,北京 100076)

为充分发挥吸气式超声速导弹巡航性能高的优势，对其巡航段的飞行方案进行了研究。考虑吸气式冲压发动机与飞行轨迹强耦合的特性，建立了以飞行攻角和燃料质量流量为双优化变量的多阶段多约束的弹道优化模型，提出了一种飞行轨迹与推力规律一体化优化设计方法。以射程最大为性能指标，对吸气式超声速导弹的爬升段和巡航段进行了综合优化设计，并着重对不同巡航方案下的弹道性能进行了分析。仿真结果表明，该方法能有效解决吸气式超声速导弹多阶段多约束轨迹优化问题，对于该吸气式超声速导弹而言，巡航的速度不宜太大，高空飞行更有利于增加射程；不等高不等速巡航方案与等高等速巡航方案相比，最大射程提高了12.3%。研究成果可为吸气式超声速导弹总体设计提供参考。

吸气式超声速导弹；多阶段多约束；巡航方案；一体化优化

0 引言

吸气式超声速导弹具有速度快、射程远、突防能力强等一系列技术优势，成为世界各国关注的研究热点[1-4]。由于采用吸气式冲压发动机作为动力装置，使得其飞行性能与推力系统之间存在强耦合的特性，在进行弹道方案设计时，必须考虑飞行轨迹与推力规律一体化优化设计。吸气式超声速导弹从助推器关机后，冲压发动机开始接力工作，导弹爬升到巡航高度和速度进行巡航飞行，飞行包络大，气动特性和发动机推力变化复杂，且受到过程约束和终端约束限制，对全弹道的性能影响较大。因此，对吸气式超声速的爬升段和巡航段的弹道方案进行综合优化设计具有重要的理论研究意义和工程应用价值。

导弹弹道优化设计是在满足各种约束的条件下，如何到达指定目标点的最优控制问题，国内外学者针对该问题做了大量的研究工作[5-14]。文献[5]用间接法对高超声速飞行器的助推-滑翔弹道进行了优化设计；文献[6]中通过将最优控制理论，将高超声速滑翔式飞行器轨迹优化转化成两点边值问题，采用遗传算法求解该两点边值问题；文献[7]采用基于Akima插值多项式的直接法求解高超声速滑翔式飞行器再入轨迹优化问题；文献[8]则利用直接法中的Legendre伪谱法对再入飞行器的轨迹进行了优化。但上述文献均是对飞行轨迹的某一阶段进行优化设计，在此基础上，文献[9]利用改进的粒子群优化算法对双脉冲导弹的多阶段非连续助推弹道方案进行了优化设计，但仍是对弹道的各阶段分开进行优化。相比于其他飞行器弹道优化设计研究，对以吸气式超声速导弹的弹道优化设计与分析开展的研究工作较少，文献[10-12]在进行以冲压发动机为动力的导弹爬升弹道优化的研究中，推力规律只根据飞行马赫数进行了适当调节，并没有参与优化，并未考虑发动机推力与飞行轨迹的相互影响作用；文献[13-14]在此基础上，研究了发动机性能与飞行状态相互影响条件下的爬升段轨迹优化设计问题，并获得了燃料最省的上升段轨迹。

本文在考虑过载、动压、终端弹道参数等约束条件的基础上，充分考虑飞行过程中吸气式冲压发动机的性能约束，选取燃料质量流量和飞行攻角作为双优化设计变量，建立了吸气式超声速导弹多阶段多约束的弹道优化模型，提出了一种基于hp自适应伪谱法的飞行轨迹与推力规律一体化优化设计与分析方法，对吸气式超声速导弹爬升段和巡航段轨迹的最大射程进行综合优化，并着重分析了巡航段的飞行方案对弹道性能的影响，从而为吸气式超声速导弹方案弹道的工程设计提供参考。

1 弹道模型

1.1 动力学模型

采用球体模型，忽略地球自转和地球曲率的影响，将导弹看作可控的质点，在铅垂平面内的吸气式超声速导弹动力学模型可简化为[15]

(1)

式中v、θ、L和m分别为导弹的飞行速度、弹道倾角、射程和质量；r为导弹与地心的距离；H为高度；Re为地球半径；g为重力加速度；P为发动机推力；X=qSCx，Y=qSCy分别为阻力和升力，由动压q和气动特性决定；S为参考面积；Cx和Cy分别为阻力系数和升力系数，可由攻角α和马赫数Ma插值计算获得；mc为发动机的燃料质量流量。

1.2 发动机推力特性分析

吸气式冲压发动机参数可参照文献[16]进行计算，从而得到冲压发动机的推力P、静压裕度Sm和余气系数αf随飞行高度H、马赫数Ma、攻角α及燃料质量流量mc的变化关系：

(2)

其中，f1、f2、f3以表格的形式给出，采用四维三次样条函数插值方式进行计算。

选取飞行典型工况下的高度分别为15、20 km，马赫数为2.5～4.0，攻角为-2°～12°，燃料质量流量为0.2～1.1 kg/s，对发动机推力进行数值计算，推力的变化曲线如图1所示。

由图1可知，当质量流量较小时，推力随高度增加而增加，当质量流量较大时，推力随高度增加而减小；推力随马赫数的增加先增加后减小，且在Ma=3.0左右推力达到最大值；攻角增加，推力先增加后减小，近似为二次函数关系，极值点在攻角在4°左右；推力随质量流量增加而增加，且呈线性变化趋势。

2 多阶段弹道优化模型

2.1 问题描述

吸气式超声速导弹一般通过飞机携带至一定的高度后投放，采用助推器使导弹加速至冲压发动机正常工作的速度后，冲压发动机开始接力工作，导弹爬升至预定的巡航高度和速度进行巡航飞行。相比于爬升段和巡航段弹道，助推段的主要作用是将导弹加速到冲压发动机能正常工作的速度，其工作时间很短，优化和非优化方案对弹道的性能影响不大。为此，本文只对爬升段和巡航段的轨迹进行优化设计。

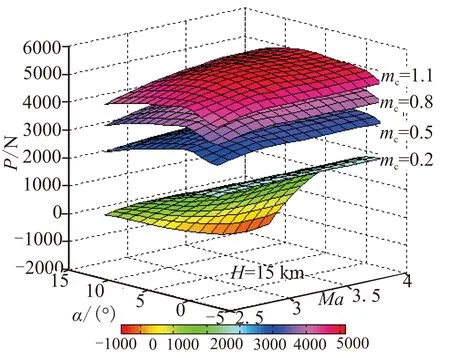
(a)高度为15 km

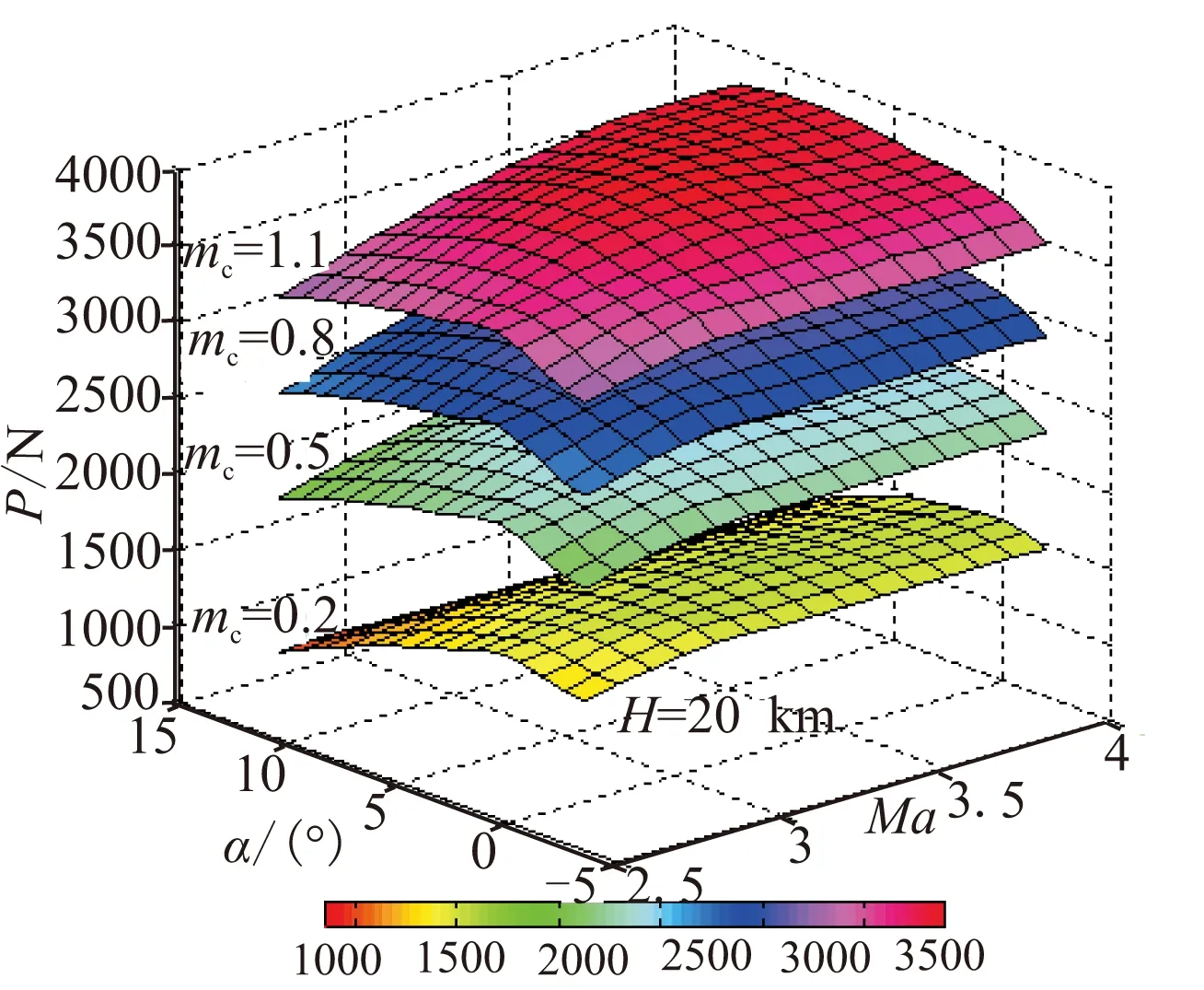
(b)高度为20 km图 1 推力变化曲线Fig.1 Curves of thrust

以最大射程为性能指标，对以下5种不同巡航方案下的爬升段和巡航段弹道进行综合优化设计和对比分析，研究巡航段的飞行方案对弹道性能的影响。

方案1：低空低速-等高等速巡航；

方案2：低空高速-等高等速巡航；

方案3：高空低速-等高等速巡航；

方案4：高空高速-等高等速巡航；

方案5：不等高不等速巡航。

2.2 约束条件

(1)终端约束

为保证吸气式超声速导弹正常巡航飞行，终端弹道参数应满足一定的约束条件，包括末端高度、速度和弹道倾角约束，即：

等高等速巡航：

不等高不等速巡航：

(2)连接点约束

为保证吸气式超声速导弹爬升段和巡航段间平滑过渡，应使得爬升段结束时刻的状态量与巡航段开始时刻的状态量对应相等，即：

式中i和i+1分别表示爬升段和巡航段；t为时间；s为状态量；下标0、f分别表示开始、结束。

(3)控制约束

考虑到冲压发动机性能及进气道攻角的限制，吸气式超声速导弹的冲压发动机燃料质量流量mc和飞行攻角α的约束条件为

(4)路径约束

考虑导弹的防热要求，动压q必须满足约束条件：

考虑导弹结构设计限制，法向过载 应限制在一定的范围内：

为充分发挥吸气式冲压发动机的性能，发动机的静压裕度Sm和余气系数αf应满足：

10%≤Sm≤100%，0.5≤αf≤3

2.3 性能指标

对吸气式超声速导弹的燃油经济性来说，就是在给定的燃油总量的情况下，导弹的射程L(tf)最远。因此，弹道优化设计的目标函数为

J=maxL(tf)

(3)

3 弹道优化方法

3.1 hp自适应伪谱法

弹道优化方法是将Radau伪谱法[16]与hp型有限元法进行融合的hp自适应伪谱法[17]。当然，hp自适应伪谱法也可采用其他伪谱法(Legendre伪谱法、Gauss伪谱法等[18-20])，本文选取Radau伪谱法的原因是容易满足网格点的连续条件[21]。

hp自适应伪谱法的离散过程与Radau伪谱法相似，通过构造全局Lagrange插值多项式逼近节点上离散后的状态量和控制量，并对插值多项式进行求导获取微分矩阵，从而将最优控制问题的求解转化为对非线性规划问题的求解。对于非线性规划问题，可采用SNOPT[22]等软件包对其进行求解。不同于Radau伪谱法，hp自适应伪谱法在迭代过程中会根据精度要求改变网格参数。当某一离散区间的计算精度不满足要求时，由hp自适应方法对该区间内的配点数h或全局插值多项式的阶次p进行自适应调整，从而使得计算时间更少，最优解的精度更高。

3.2 一体化优化设计

吸气式超声速导弹的一体化设计涉及外形、推进、气动力、气动热、结构、控制和弹道等多个相互耦合系统，根据目前的设计需求，主要考虑气动力、推进和弹道之间的耦合，对吸气式超声速导弹进行飞行轨迹与推力规律一体化优化设计，设计框架如图2所示。

选取吸气式超声速导弹飞行的攻角和发动机的燃料质量流量作为优化设计变量，并确定状态量和设计变量的初值及设计约束，进行弹道一体化优化仿真。优化过程中根据需求调用推进模型和气动力计算模型，调整设计变量，协调各子系统之间的关系，根据推力、气动力及设计变量进行弹道优化解算。上述过程多次重复，每次弹道优化仿真结束，判断当前优化设计变量方案是否达到导弹性能目标最优的条件，若满足条件，则优化设计过程结束；否则进行新方案优化设计，直到获得满足发动机工作约束并使得总体弹道性能最优的发动机的推力调节规律和飞行攻角方案，从而实现吸气式超声速导弹飞行轨迹与推力规律一体化优化设计。

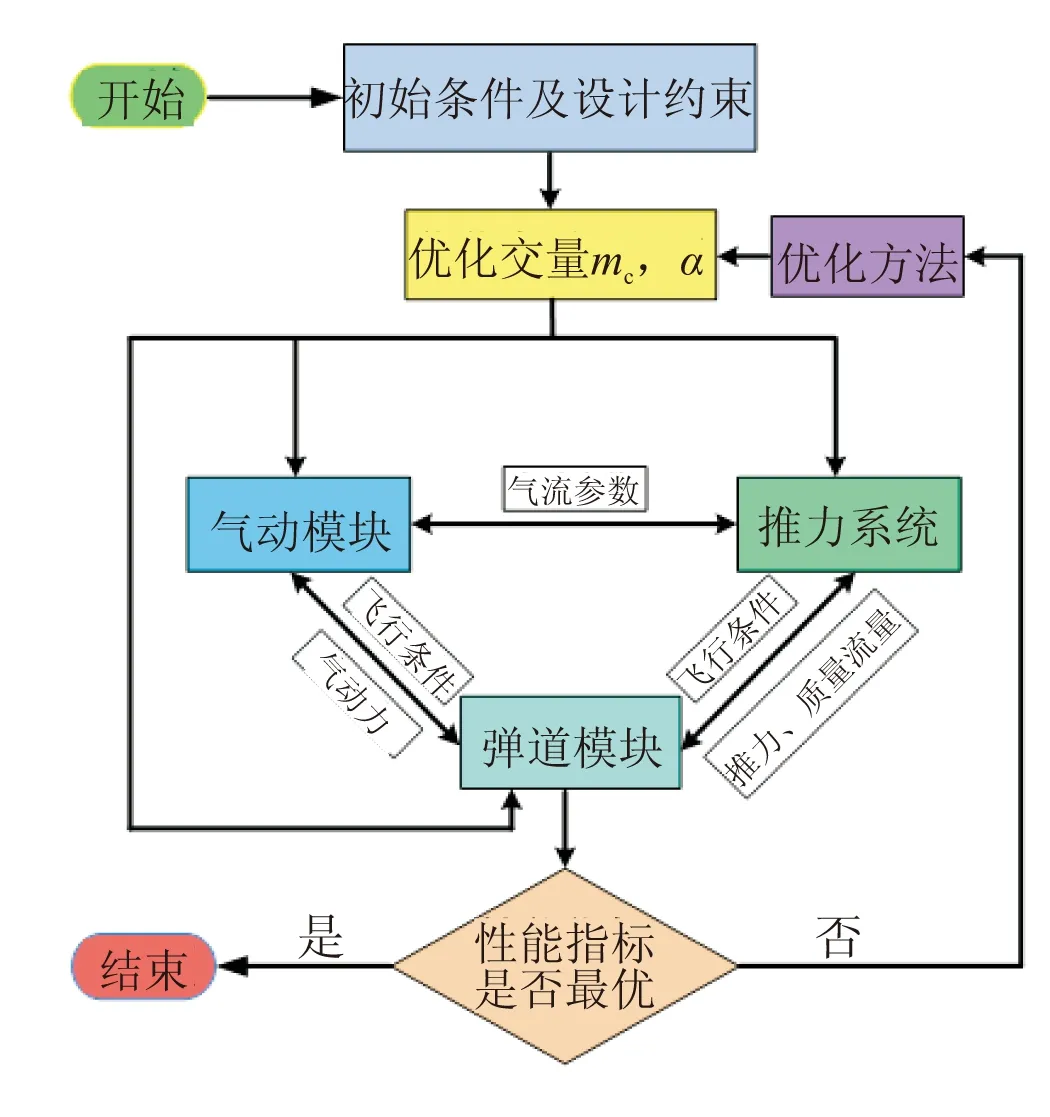
图 2 吸气式超声速导弹一体化优化设计框架Fig.2 Integrated optimization design frame of air-breathing supersonic missile

4 弹道优化方法

以某吸气式超声速导弹为研究对象，对多阶段多约束的飞行轨迹与推力规律一体化优化设计方法进行优化仿真验证。为了进一步分析巡航飞行方案对弹道性能的影响，分别对上述的5种巡航方案下的爬升段和巡航段弹道进行综合优化对比仿真。

4.1 仿真条件

吸气式超声速导弹状态变量的初始条件：Ma= 2.6，θ0=0°，L0=0 km，H0=12 km，m0=500 kg；

轨迹优化设计变量的约束条件：0.2 kg/s≤mc≤1.2 kg/s，-2°≤α≤12°；

路径约束条件：|ny|≤4，q≤150 kPa；

飞行轨迹终端的约束条件：mf=400 kg；

低空低速-等高等速巡航：Ma=3.5，Hcruise=18 km；

低空高速-等高等速巡航：Ma=4.0，Hcruise=18 km；

高空低速-等高等速巡航：Ma=3.5，Hcruise=20 km；

高空高速-等高等速巡航：Ma=4.0，Hcruise=20 km；

不等高不等速巡航：Ma∈[3.5,4.0]，Hf∈[18,20]km。

4.2 仿真结果分析

根据4.1节中的仿真条件，分别对5种巡航方案下的吸气式超声速导弹爬升段和巡航段进行一体化优化仿真，表1给出了各巡航方案下的最大射程，对比仿真曲线如图3～图10所示。

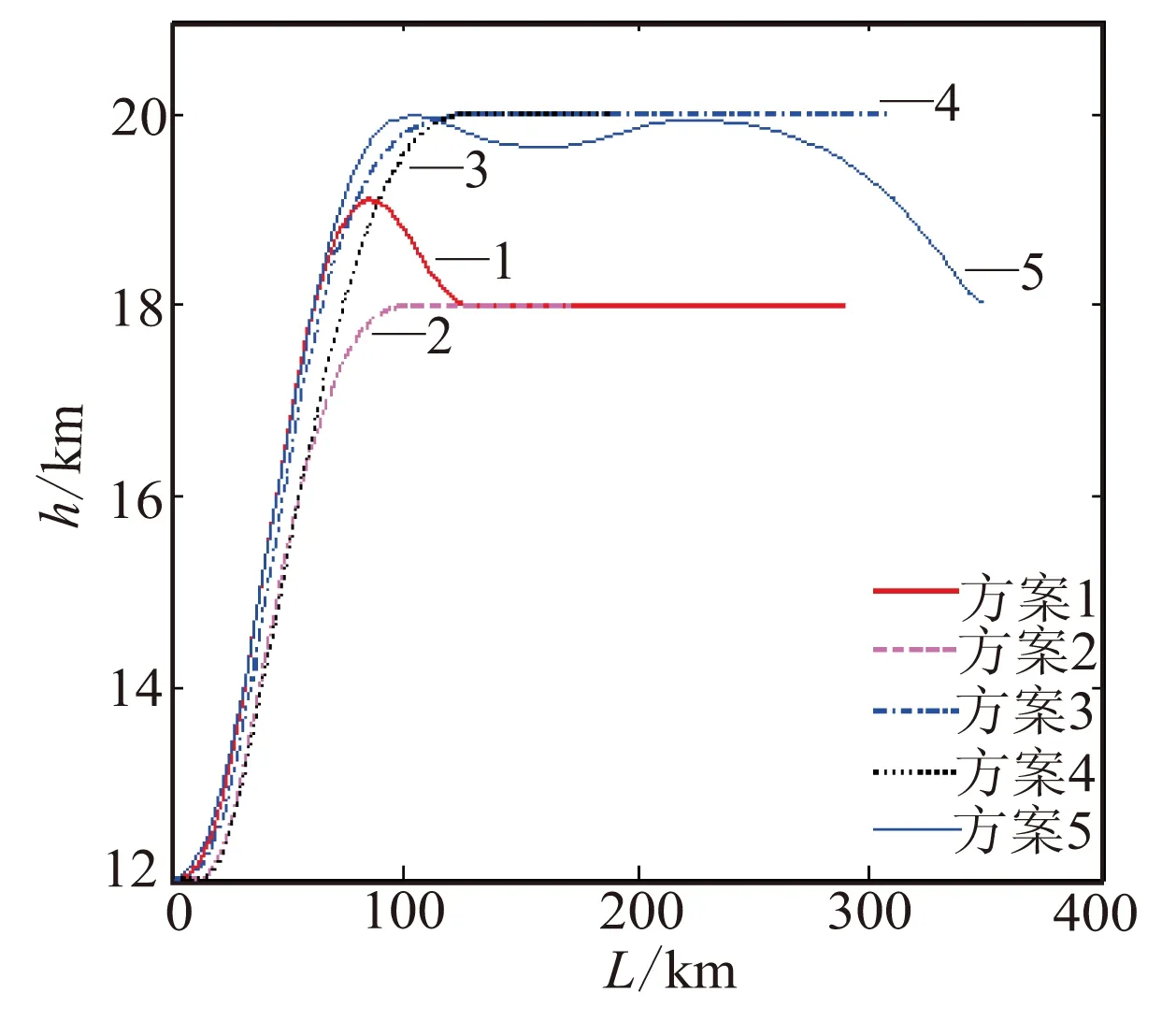
图 3 弹道曲线Fig.3 Curves of trajectory

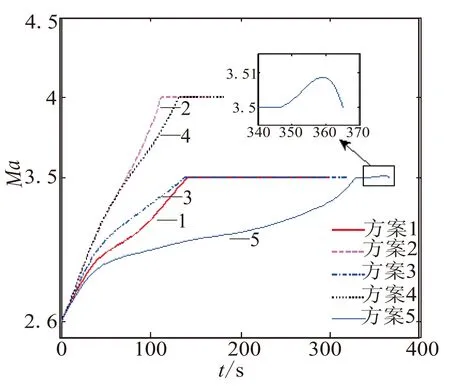
图 4 马赫数变化曲线Fig.4 Curves of Mach number

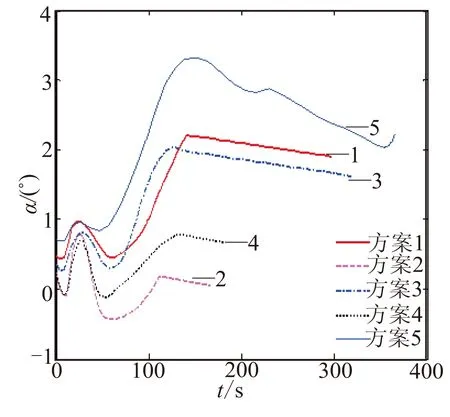
图 5 攻角变化曲线Fig.5 Curves of angle of attack

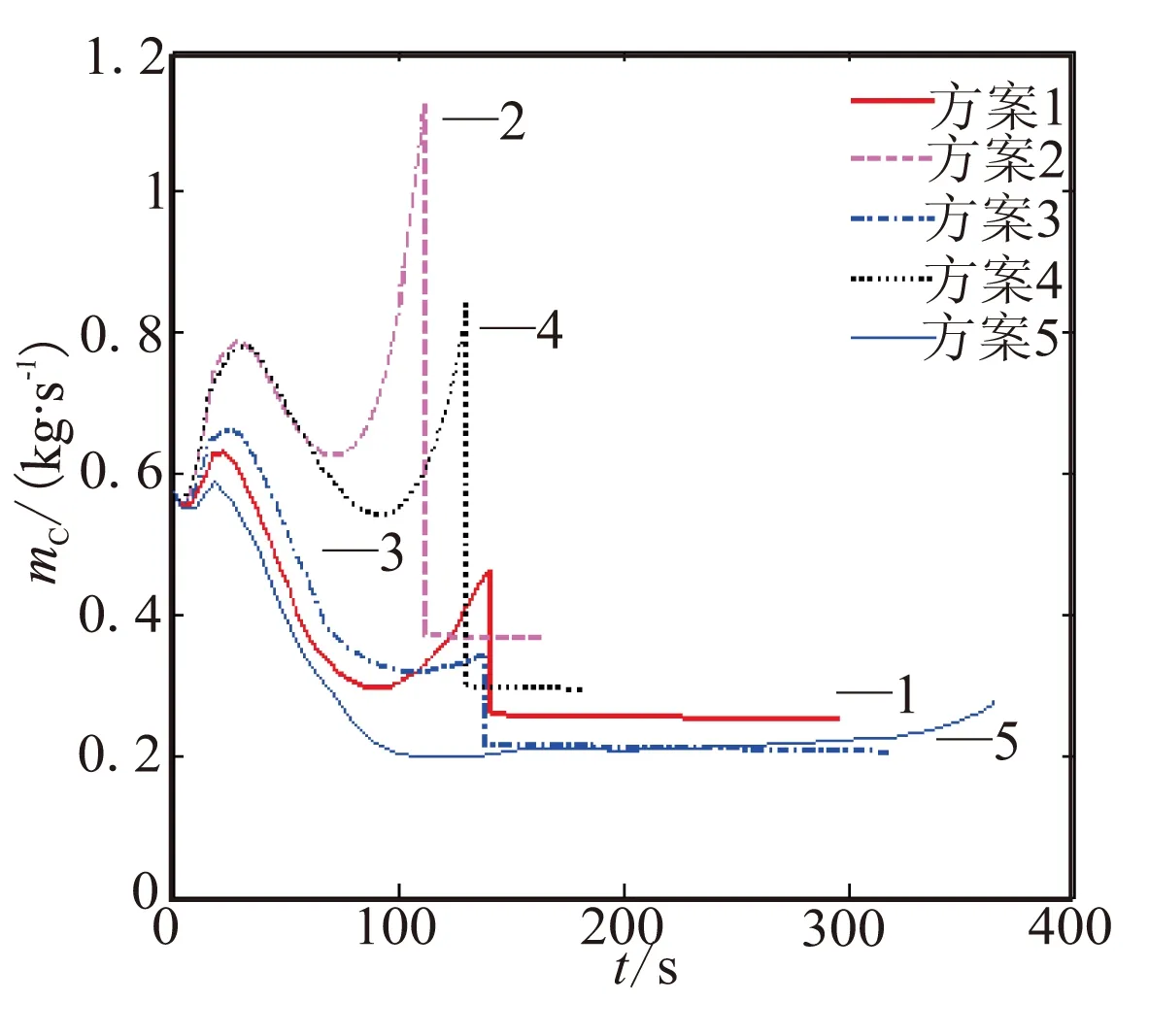
图 6 燃料质量流量变化曲线Fig.6 Curves of fuel flow rates

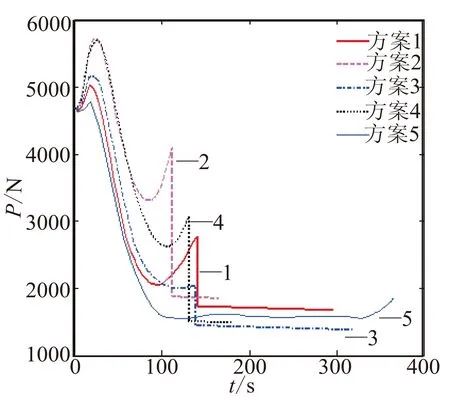
图 7 推力变化曲线Fig.7 Curves of thrust

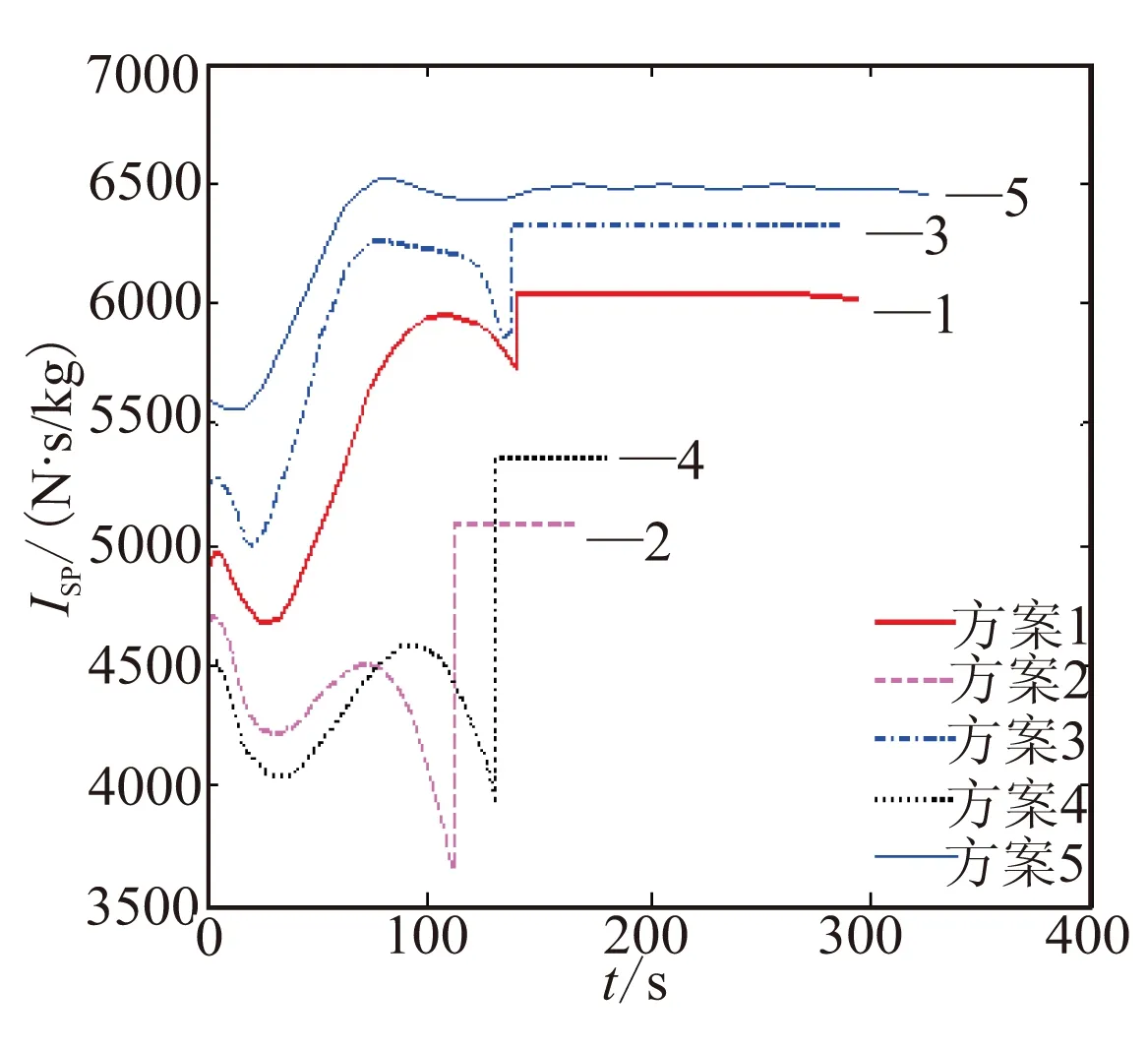
图 8 比冲变化曲线Fig.8 Curves of specific impulse

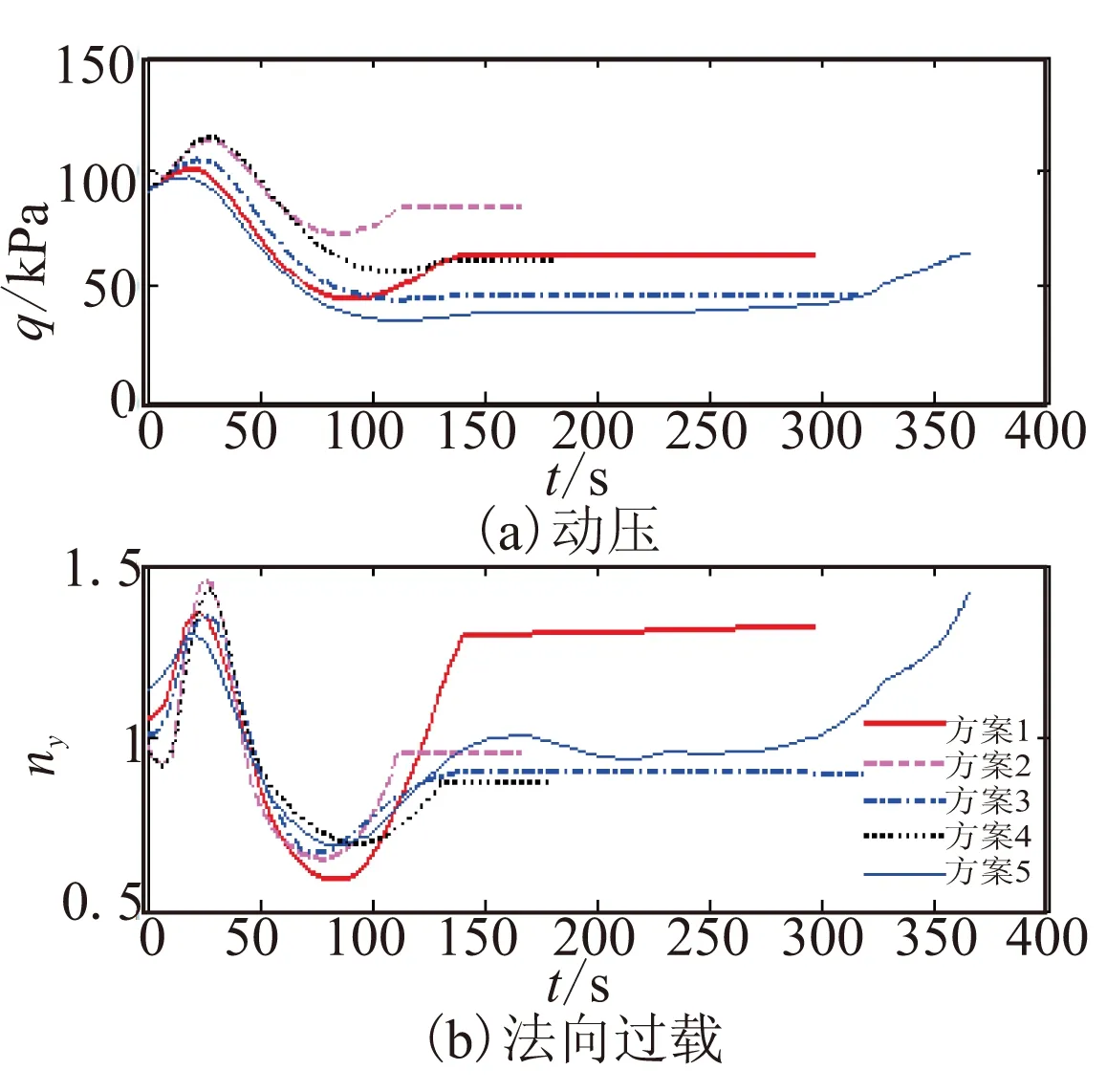
图 9 动压和法向过载变化曲线Fig.9 Curves of dynamic pressure and normal overload

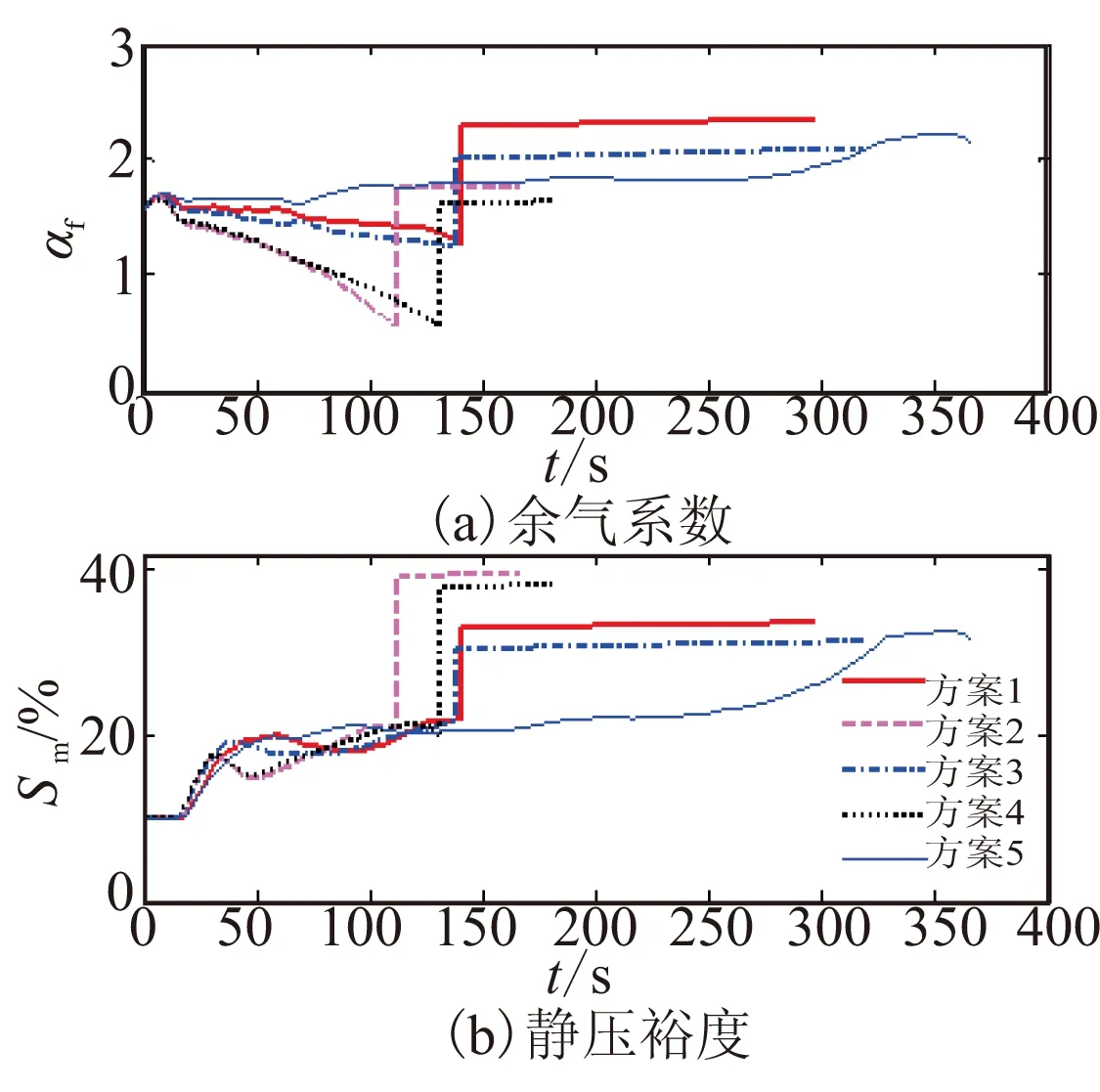
图 10 余气系数和静压裕度变化曲线Fig.10 Curves of excess coefficient and static margin表 1 不同巡航方案下的最大射程Table 1 Maximum range of different cruise schemes

方案12345射程/km288.84172.15310.31188.51348.38

表1为各巡航方案下的最大射程对比值，将方案1与方案2(方案3与方案4)进行对比可得出：对于该吸气式超声速导弹而言，在高度为18～20 km和速度为Ma=3.5～4.0的巡航飞行包络内时，同一巡航高度下，巡航速度越低，射程越大；方案1与方案3(方案2与方案4)对比可看出，在相同的巡航速度条件下，巡航高度越高，射程越大。若采用等高等速方案巡航，高空低速-等高等速巡航的射程最大为310.31 km，相比于各等高等速巡航方案下的最大射程，不等高不等速巡航方案的射程为348.38 km，射程提高了约12.3%。

从图3和图4可看出，相比于方案1的飞行弹道，方案2爬升段的飞行速度高，飞行高度低，使得气动阻力大，造成较大的能量损耗，使得发动机性能浪费，进而导致射程能力下降。方案4相比于方案3的射程小的机理与上述相同。而方案5相比于其他方案，爬升段飞行时速度较低，飞行高度较高，阻力做功的能量损耗低，这种爬升方式能够有效地增加导弹的飞行射程。

从图8可看出，对于巡航段的飞行弹道，不等高不等速巡航方案相比各个等高等速巡航方案，通过协调高度和速度的变化规律，冲压发动机的比冲Isp较大，使得发动机的工作效率较高，节省燃料，有利于增加导弹的射程能力。从状态量的变化曲线可看出，优化后的状态量在爬升段和巡航段的转接点处是连续的，从而说明引入连接点约束处理多阶段优化问题方法的正确性。

从图5～图7可看出，各方案下的攻角曲线变化差别不大，且均小于4°，保证了吸气式冲压发动机具有较好的进气状态，而推力的变化趋势与质量流量的变化趋势基本一致。由此可看出，相比于攻角对推力的影响，质量流量对推力的影响较大。图6中的等高等速方案下的燃料质量流量变化曲线在爬升段与巡航段的转接点有一个突降，这是因为吸气式超声速导弹高空的气动阻力较小，需减小发动机推力以保持等速巡航，这也使得吸气式发动机的余气系数和静压裕度(图10)出现突变。

由图9和图10可看出，过程约束变量动压、过载、余气系数和静压裕度均满足设计约束。

5 结论

(1)针对吸气式超声速导弹发动机与飞行轨迹的耦合特性，将冲压发动机推力规律与弹道优化协调起来，建立了双控制变量及多阶段多约束的轨迹优化模型，利用hp自适应伪谱法构造了一种较为通用的一体化优化求解策略，以射程最大为目标函数，并对各巡航方案下的吸气式超声速导弹的爬升段和巡航段弹道进行了综合优化设计，仿真结果验证了该方法在解决多阶段多约束轨迹一体化优化问题上的有效性以及优化模型的合理性。

(2)为充分发挥冲压发动机性能，从增加导弹射程的角度，吸气式超声速导弹在高度为18～20 km和速度为Ma=3.5～4.0的包线内等高等速巡航飞行时，对于相同的巡航高度，巡航速度越低，射程越远；在同一巡航速度下，巡航高度越高越有利于增加射程。

(3)对于给定的飞行包络内，采用不等高不等速巡航方案，导弹的最大射程为348.38 km，相比于等高等速巡航方案的最大(高空低速-等高等速巡航)射程310.31 km，射程提高了12.3%。

(4)对于采用此种气动布局和冲压发动机特性的这类飞行器，从增加射程能力角度，在爬升段应尽快拉升高度，再实现加速到巡航段工作需求的马赫数和高度，以降低低空阻力做功能量损失的影响；在巡航段采用不等高不等速的设计方案，保证冲压发动机始终以大比冲性能进行飞行，使得整段弹道的发动机的工作效率较高，阻力做功能量损失小，从而增加导弹的射程能力。

[1] Randall T V,Lawrence D H,Charles R M.X-43A hypersonic vehicle technology development[J].Acta Astronautica, 2006,59(1-5):181-191.

[2] 马辉, 袁建平, 方群. 吸气式高超声速飞行器动力学特性分析[J].宇航学报,2007, 28(5):1100-1104.

[3] Pu Z Q,Tan X M,Fan G L,et al.Uncertainty analysis and robust trajectory linearization control of a flexible air-breathing hypersonic vehicle [J].Acta Astronautica,2014,101(1):16-32.

[4] 唐硕, 祝强军. 吸气式高超声速飞行器动力学建模研究进展[J].力学进展, 2011, 41(2):187-200.

[5] Chuang C H.Hitoshi morimoto periodic optimal cruise for a hypersonic vehicle with constrains [J] .Journal of Spacecraft and Rockets, 1997, 34(2):165 -171.

[6] 周浩,周韬,陈万春, 等.高超声速滑翔飞行器引入段弹道优化[J].宇航学报, 2006, 27(5) :970-973.

[7] 陈小庆,侯中喜,刘建霞.高超声速滑翔式飞行器再入轨迹多目标多约束优化[J] .国防科技大学学报,2009, 31(6):77-83.

[8] Rao A V, Clarke K A. Performance optimization of a maneuvering re-entry vehicle using a Legendre pseudo-spectral method[R]. AIAA 2002-4885.

[9] 程仙垒, 彭双春, 郑伟, 等. 多约束条件下非连续助推弹道方案设计与优化[J].系统工程与电子技术, 2015,37(4):888-894.

[10] 王华, 杨存富, 刘恒军. 以冲压发动机为动力的导弹爬升弹道研究[J].现代防御技术, 2008,33(2):27-30.

[11] 侯宏录, 柳长安, 周德云,等. 巡航导弹加速爬升段弹道优化设计[J].飞行力学, 2006,24 (1):45-47.

[12] 王华, 杨存富, 刘恒军. 以冲压发动机为动力的导弹爬升弹道优化[J].弹箭与制导学报, 2008,28(3):185-187.

[13] 尚腾, 谷良贤, 赵吉松, 等. 冲压发动机导弹爬升轨迹与推力调节规律优化[J].飞行力学,2012,30(3):280-283.

[14] 龚春林,韩璐.RBCC可重复使用运载器上升段轨迹优化设计[J].固体火箭技术, 2012,35(3):290-295.

[15] 赵汉元.飞行器再入动力学与制导[M].长沙: 国防科技大学出版社, 1997.

[16] 李浩. 吸气式高超声速飞行器气推耦合特性研究[D].哈尔滨: 哈尔滨工业大学, 2013.

[17] Fahroo F,Ross I M.Pseudospectral methods for infinite-horizon nonlinear optimal control problem[J].Journal of Guidance,Control,and Dynamic,2008,3(4):927-2936.

[18] Darby C L, Hager W W, Rao A V.Direct trajectory optimization using a variable low-order adaptive pseudospectral method[J].Journal of Spacecraft and Rockets, 2011,48(3):433-2445.

[19] Shamsi M,Dehghan M. Determination of a control functions in three-dimensional parabolic equations by Legendre pseudo-spectral method[J].Numerical Methods for Partial Differential Equations,2012,28(1):74-93.

[20] Huntington G T,Rao A V.Optimal reconfiguration of spacecraft formations using the Gauss pseudospectral method[J].Journal of Guidance, Control,and Dynamic,2008,31(3):689-2698.

[21] Darby C L,Hager W W,Rao A V.Direct trajectory optimization using a variable low-order adaptive pseudo-spectral method[J].Journal of Spacecraft and Rockets, 2011,48(3):433-2445.

[22] Gill P E, Murray W, Saunders M A. SNOPT:An SQP algorithm for large scale constrained optimization[J].SIAM Journal on Optimization,2002,12(4):979-21006.

(编辑：吕耀辉)

Trajectory optimization design and analysis for air-breathing supersonic missile

MING Chao1,SUN Rui-sheng1,LIANG Zhuo2,BAI Hong-yang1

(1.School of Energy and Power Engineering, NUST, Nanjing 210094, China;2.China Academy of Launch Vehicle Technology,Beijing 100076,China)

In order to take advantage of the high performance of the air-breathing supersonic missile, the cruise scheme was investigated. Considering the strong coupling between the air-breathing ramjet and flight profile, a multiple phases and multiple constraints trajectory optimization model was established with double optimization design variables composed of angle of attack and fuel flow rate, and a trajectory and ramjet integration optimal design method was proposed. The climb and cruise trajectory were optimized synthetically by selecting the maximum range as the performance index. Moreover, the performances of trajectory under different cruise schemes were mainly analyzed. The simulation results show that the proposed method is effective in solving the optimization design problem with multiple constraints and phases for air-breathing supersonic missile. In term of this missile, the cruise velocity should not be too high, and it is conducive to increase range at high altitude. The maximum rang of the cruise scheme of non-constant altitude and non-constant velocity is improved by 12.3% in comparison to the cruise scheme of constant altitude and constant velocity. The research results can provide reference for overall design of the air-breathing supersonic missile.

air-breathing supersonic missile；multiple phases and multiple constraints；cruise scheme；integral optimization design

2015-11-18；

2015-12-15。

国家自然科学基金NSAF联合基金(11176012)；江苏省普通高校研究生科研创新计划工程(KYLX15-0394)。

明超(1989—)，男，博士，研究方向为先进弹道优化理论与控制技术。E-mail：nust802mc@126.com

孙瑞胜(1976—)，男，副教授，研究方向为导弹制导与控制技术。E-mail：srscom@163.com

V412

A

1006-2793(2016)06-0833-06

10.7673/j.issn.1006-2793.2016.06.017