水产品贮运过程品质预测技术研究进展

刘晓畅, 罗永康

(中国农业大学食品科学与营养工程学院, 北京 100083)

水产品贮运过程品质预测技术研究进展

刘晓畅, 罗永康*

(中国农业大学食品科学与营养工程学院, 北京 100083)

水产品在贮运过程中受到微生物和生化反应的作用品质会迅速下降。通过水产品的品质指标检测了解水产品品质，存在着耗时、耗力等缺点，不能即时监控水产品在贮运过程中的品质变化。水产品品质预测技术是借助数学模型模拟并预测水产品的品质，借助该技术可以实现对水产品品质的快速预测。文章介绍并分析了目前已有的几类水产品品质预测模型，包括动力学模型、微生物生长预测模型、基于整体稳定性指数的数学模型和人工智能数学模型，以期为各类水产品品质预测技术的建立和完善提供参考。[中国渔业质量与标准, 2016, 6(2):1-6]

水产品；预测技术；贮运；模型

近年来，随着人们生活质量的不断提高,对于水产品的消费需求也越来越大，大部分水产品在捕捞后需要经过运输、贮藏等环节才能到达消费者手中。而在贮运过程中，在外源微生物和内源酶的共同作用，水产品的品质会迅速下降，从而影响其食用价值和加工适性[1]。通过检测水产品的理化和微生物指标，可以了解水产品的鲜度。但传统基于理化指标和微生物指标的检测，既耗时又耗力，不能及时地对贮运过程中的指标变化情况进行监控，在实际生产中的应用效果不佳[2]。因此，水产品品质预测技术应运而生。

水产品品质预测技术是一门综合食品科学、微生物学、化学、计算机科学和数学等多个学科发展而来的技术。主要借助数学模型对水产品的品质进行预测，从而准确并提前了解水产品的品质情况，以较少的成本实现对水产品质量和安全的快速评估和预测，为水产品的加工和销售提供指导。

目前已有很多水产品品质预测模型，且不同的模型适用条件和对象不同。因此要进行水产品品质的预测，首先要明确影响水产品品质的因素，并据此选择合适的模型[3]。文章主要阐述了目前已有的水产品品质预测模型，并简要介绍了各类模型的应用状况，以便为今后水产品的品质预测研究提供参考。

1 动力学预测模型

动力学预测模型是描述食品品质和贮藏时间、温度的函数。首先，品质衰变动力学原理描述了食品品质和贮藏时间的关系，而品质衰变动力学与贮藏温度的关系可用Arrhenius模型、Q10模型和Z值模型等描述，其中Arrhenius模型的应用最广。因此，动力学预测模型的建立是基于品质衰变动力学原理和Arrhenius模型。

1.1 品质衰变动力学原理

水产品在贮运过程中品质指标的变化遵循品质衰变动力学原理，如式(1)所示[4]。

-dC/dt=k×Cn

式(1)

式(1)中：C为品质指标，t为时间；dC/dt为品质变化速率；k为品质变化速率常数；n为反应级数。

对于不同衰变特征的品质指标，需要由相应级数(n)的品质衰变函数来描述其变化规律[5]。对式(1)积分，可得到不同反应级数的品质函数表达式(表1)。

品质指标反应级数的确定要利用已有的指标测定值进行线性回归分析，分别对品质指标的不同形式(C、lnC和1/C)与时间的关系进行线性回归分析，根据相关系数来比较不同级数品质函数所对应的拟合精度，最终选择最合适的反应级数。利用拟合方程，可以计算出水产品在特定贮藏条件下，品质指标C达到任一特定值所需要的时间以及任一时间t对应的品质值。

表1 不同反应级数的品质函数
Tab.1 Quality function with different reaction orders

反应级数(n)Reactionorder品质函数f(t)Qualityfunction0C-C0=k×t1lnC-lnC0=-k×t21/C-1/C0=k×t

注：C0为品质指标C的初始值;k为品质变化速率常数t为时间。

1.2 Arrhenius方程

品质函数中的变化速率常数k受多种因素(温度、pH、湿度、光照和压力等)的影响，其中温度对其影响最大。通常，品质变化速率常数与温度的关系符合Arrhenius方程[6]，见式(2)。

k=k0×exp [-Ea/(R×T)]

式(2)

式(2)中：k0为指前因子；Ea为表观活化能；R为气体常数，取值为8.314 J/(mol·K)，T为绝对温度。

1.3 动力学预测模型的应用

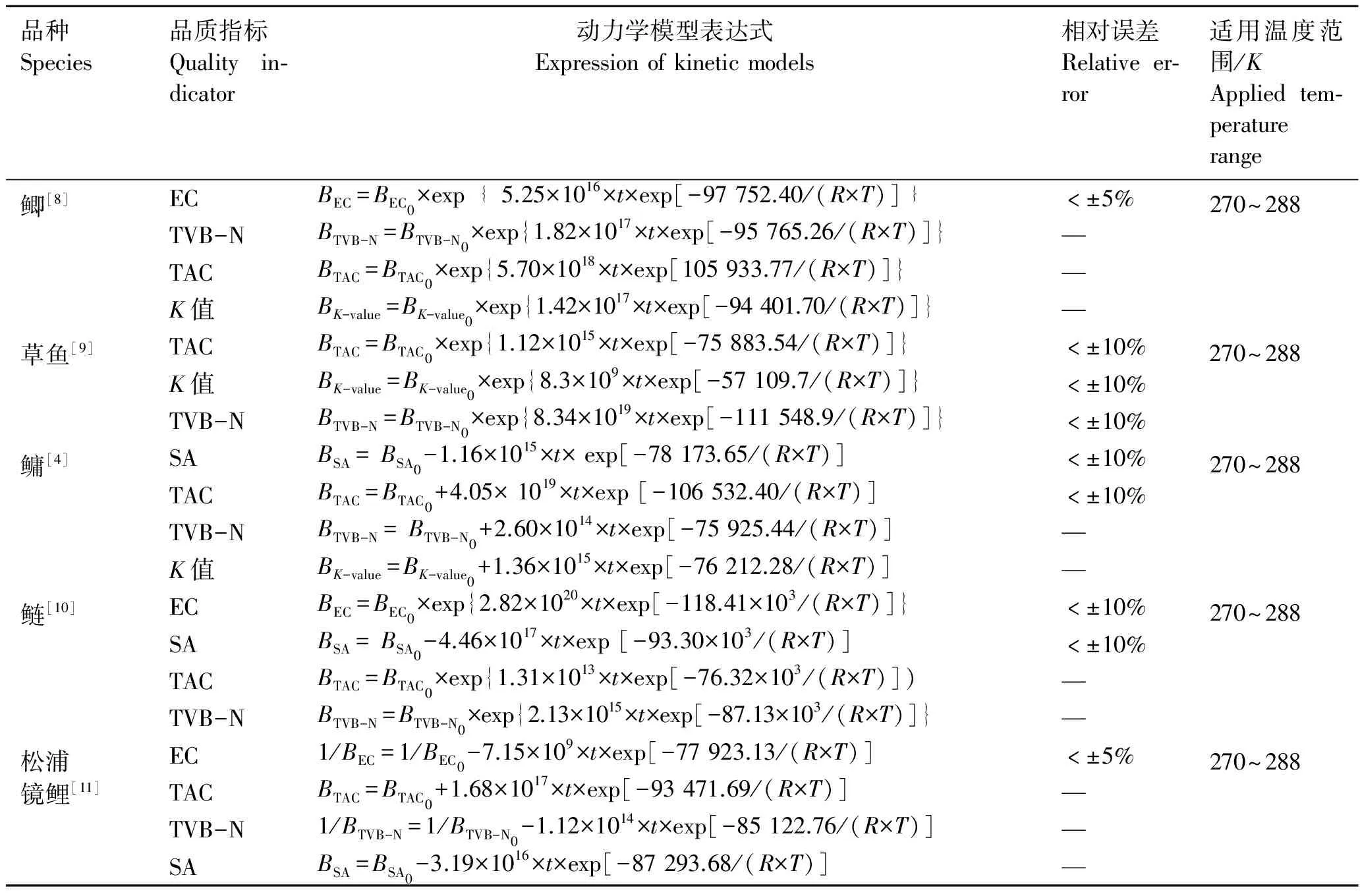
动力学预测模型已被广泛应用于水产品品质预测的研究中。Hong等[4, 8-11]测定了多种淡水鱼片在不同温度贮藏条件下品质指标的变化情况，建立了淡水鱼在贮藏过程中品质变化的动力学预测模型体系，如表2所示。

表2 不同淡水鱼类在贮藏过程中品质指标变化的动力学预测模型
Tab.2 Kinetic models for the quality prediction of different freshwater fish during storage

品种Species品质指标Qualityin⁃dicator动力学模型表达式Expressionofkineticmodels相对误差Relativeer⁃ror适用温度范围/KAppliedtem⁃peraturerange鲫[8]ECTVB-NTACK值BEC=BEC0×exp﹛5．25×1016×t×exp[-97752．40/(R×T)]﹜BTVB-N=BTVB-N0×exp{1．82×1017×t×exp[-95765．26/(R×T)]}BTAC=BTAC0×exp{5．70×1018×t×exp[105933．77/(R×T)]}BK-value=BK-value0×exp{1．42×1017×t×exp[-94401．70/(R×T)]}﹤±5%———270～288草鱼[9]TACK值TVB-NBTAC=BTAC0×exp{1．12×1015×t×exp[-75883．54/(R×T)]}BK-value=BK-value0×exp{8．3×109×t×exp[-57109．7/(R×T)]}BTVB-N=BTVB-N0×exp{8．34×1019×t×exp[-111548．9/(R×T)]}﹤±10%﹤±10%﹤±10%270～288鳙[4]SATACTVB-NK值BSA=BSA0-1．16×1015×t×exp[-78173．65/(R×T)]BTAC=BTAC0+4．05×1019×t×exp[-106532．40/(R×T)]BTVB-N=BTVB-N0+2．60×1014×t×exp[-75925．44/(R×T)]BK-value=BK-value0+1．36×1015×t×exp[-76212．28/(R×T)]﹤±10%﹤±10%——270～288鲢[10]ECSATACTVB-NBEC=BEC0×exp{2．82×1020×t×exp[-118．41×103/(R×T)]}BSA=BSA0-4．46×1017×t×exp[-93．30×103/(R×T)]BTAC=BTAC0×exp{1．31×1013×t×exp[-76．32×103/(R×T)])BTVB-N=BTVB-N0×exp{2．13×1015×t×exp[-87．13×103/(R×T)]}﹤±10%﹤±10%——270～288松浦镜鲤[11]ECTACTVB-NSA1/BEC=1/BEC0-7．15×109×t×exp[-77923．13/(R×T)]BTAC=BTAC0+1．68×1017×t×exp[-93471．69/(R×T)]1/BTVB-N=1/BTVB-N0-1．12×1014×t×exp[-85122．76/(R×T)]BSA=BSA0-3．19×1016×t×exp[-87293．68/(R×T)]﹤±5%———270～288

注：t为贮藏时间；T为贮藏温度；B0为指标初始值；B为经过时间t后的指标值；EC为电导率；TVB-N为挥发性盐基氮值；TAC为菌落总数；SA为感官评分。—表示无。

2 微生物生长预测模型

水产品在贮藏过程中只有少数微生物参与腐败过程，并产生具有臭味或异味的代谢产物，这些腐败微生物就是该水产品的特定腐败菌(specific spoilage organisms，SSOs)[12]。SSOs是造成水产品腐败的主要原因，因此依据SSOs的生长状况可以判断水产品的品质和剩余货架期[13]。微生物生长预测模型是利用数学模型模拟微生物的生长状况，通常它可分为一级模型、二级模型和三级模型[14]。

2.1 一级模型及应用

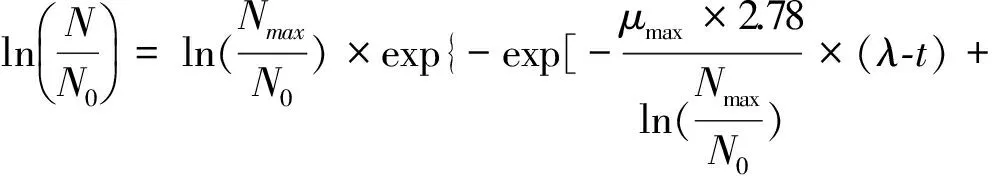
1]}

式(3)

式(3)中，t为贮藏时间，N为时间t时的菌落总数，N0为初始菌落总数，Nmax为N的最大值，μmax为微生物的最大比生长速率，λ为微生物生长的延滞时间。

崔正翠等[16]利用大菱鲆(Penaeusnotialis)在273、276、240和283 K贮藏条件下特定腐败菌——希瓦氏菌的生长数据，建立了描述希瓦氏菌生长状况的Gompertz模型。李学英等[17]首先确定了有氧包装鲤(Cyprinuscarpio)在冷藏条件下的优势腐败菌是假单胞菌，然后利用修正的Gompertz方程构建了假单胞菌在273～288 K条件下的生长模型，该模型能准确描述假单胞菌在该温度范围内的生长状况。Dabadé等[18]研究了Pseudomonaspsychrophila和Carnobacteriummaltaromaticum在热带对虾(Penaeusnotialis)中的生长情况，并建立了这两种腐败菌生长的修正Gompertz模型和Baranyi模型，结果表明修正Gompertz模型的拟合优度优于Baranyi模型。

2.2 二级模型及应用

二级模型是描述环境因子(温度、pH、水分活度等)对一级模型中参数的影响，其中温度是研究最多的环境因子。常见的二级模型包括平方根模型、Arrhenius模型、主要参数模型和响应面模型等。

Mejlholm等[19]利用6个二级模型(4个主要参数模型、1个平方根模型和11个神经网络模型)模拟即食水产食品中Listeriamonocytogenes的生长情况，并比较了这6种模型的拟合性能，结果表明模型中包含的环境因子越多，则模型的拟合性能越好，越接近Listeriamonocytogenes的真实生长情况。随后，Mejlholm等[20]建立了在12个环境因子(乙亚硝酸盐、醋酸、安息香、柠檬、山梨酸、温度等)作用下，水产品中嗜冷乳杆菌生长情况的主要参数模型。Dabadé等[18]在Gompertz模型的基础上，进一步利用平方根模型和Arrhenius模型研究了温度对Pseudomonaspsychrophila最大比生长速率的影响，并分别利用恒定温度和波动温度验证了模型的可行性。García等[21]利用Logistic模型和平方根模型建立了鳕(Merlucciusmerluccius)中腐败菌的生长预测模型。

2.3 三级模型及应用

三级模型是将一个或多个一级模型和二级模型整合起来的软件化模型。三级模型将原始数据模型和计算机软件结合起来，使用者只需输入微生物生长的相关数据(如温度、时间、pH等)，即可搜索到与之相符的数据档案，微生物预测模型软件的应用大大增加了模型的实际应用功能。三级模型的功能主要有预测微生物在变动的环境条件下的生长变化；比较不同环境条件下微生物的生长情况；比较不同微生物在相同环境条件下的生长情况等。

Dalgaard等[22]开发了针对海洋食品的腐败与安全预测程序(seafood spoilage and safety predictor，SSSP)软件，该软件包含了特定腐败菌的生长模型和腐败模型的相关速率以及不同腐败菌产生组胺的模型，据此可以估测恒温或波动温度条件下特定腐败菌的数量、组胺的含量以及产品的货架期。Dalgaard[23]在SSSP基础上又进一步发展了食品腐败与安全预测程序(food spoilage and safety predictor, FSSP)软件，该程序增加了乳酸菌的生长模型以及乳酸菌和单增李斯特菌的交互生长模型。目前，中国水产科学研究院东海水产研究所也开发了可用于罗非鱼(Oreochromisniloticu)品质预测的系统(fish shelf life predictor，FSLP)[24]。

3 其他新模型

3.1 基于整体稳定性指数的数学模型

由于一些食品体系的复杂性或指标的多样性，往往会遇到多个指标反而更难清晰地反映食品在贮藏过程中品质变化的问题[3]。此时，可先借助统计学的方法，将繁杂的多指标问题转化成一个或少数几个独立变量的问题。整体稳定性指数法(global stability index，GSI)是同步考虑食品在贮藏过程中多个指标的变化，然后根据不同指标的重要性为其分配不同的权重系数，最后把这些品质变化整合成一个单一的指标来反映产品的整体品质特性。Hong等[25]首先将整体稳定性指数引入水产品的品质预测，按照不同的权重系数将感官评分、TVB-N、菌落总数、K值整合单一的指标——GSI，利用GSI预测鳙(Aristichthysnobilis)鱼头在不同冷藏温度下整体品质变化的情况，结果表明该模型可以很好地预测鳙鱼头在270～288 K贮藏条件下的整体品质变化。此外，Bao等[26]和Zhu等[27]分别建立了武昌鱼(Megalobramaamblycephala)和异育银鲫(Carassiusauratusgibelio)在冷藏过程中基于GSI的品质预测模型。但目前已有的GSI预测模型还存在一些问题，例如如何更合理地选择权重系数，今后可以尝试通过运用其他统计学方法(如灰色模型)或者调查消费者的喜好来确定更合理的权重系数。

3.2 Weibullian模型

Gacula等首次将失效的概念引入食品，认为食品品质随时间的延长而下降，最终降低到人们拒绝食用的程度，即为食品失效，食品失效时间的分布从理论上符合Weibullian模型[28-29]。Corradini等[30]对Weibullian模型稍作变形后得到了可用于食品品质预测的模型，如式(4)所示。

C(t)=C0×exp [-b(T) ×tn(T)]

式(4)

式(4)中，C(t)代表指标C在时间t时的数值，C0代表指标C的初始值，b(T)表示反应速率，n(T)表示反应级数，其中b(T)和n(T)与温度有关。利用非线性回归分析可求得未知参数——b(T)和n(T)。

Barraza等[31]研究了大西洋鲑(Salmosalar)在不同冻藏温度(268、264、260和255 K)下盐溶性蛋白、硬度、黏性和咀嚼性的变化规律，并利用Weibullian模型拟合这些指标的变化情况，结果表明，Weibullian模型可以准确反映盐溶性蛋白、硬度、黏性和咀嚼性的变化情况。

3.3 人工智能数学模型

人工智能数学模型主要包括神经网络模型和贝叶斯模型等数学模型。Liu等[7]将人工神经网络模型应用于水产品的品质预测中，首先分别测定了虹鳟(Oncorhynchusmykiss)在270、273、276、282和288 K贮藏温度下感官评分、菌落总数、K值和电导率的变化，随后利用实验数据建立了描述品质指标变化与温度和时间关系的动力学模型和前馈型人工神经网络模型。结果表明，人工神经网络模型可以准确预测虹鳟鱼片感官评分、K值、电导率和菌落总数的变化情况，预测值和实测值之间的相对误差均在±10%以内，而动力学模型只能准确预测电导率和菌落总数的变化，对感官评分、K值的预测效果较差。Wang等[32]建立了径向基人工神经网络模型，用以预测盐腌武昌鱼在冷藏条件下的品质指标(感官评分、菌落总数、K值、TVB-N、硫代巴比妥酸值和肌苷含量)变化情况。表3对传统的动力学模型和人工神经网络模型进行了比较。神经网络模型最大的优点是具有自主学习能力和适用性很高[33]。因此，在今后的研究中，应尝试将更多地人工智能数学模型应用于水产品的品质预测中。

表3 人工神经网络模型和动力学模型的比较
Tab.3 Comparison of artificial neural network model and kinetic model

4 结论与展望

对于一种水产品可以尝试用不同的品质预测模型对其品质进行模拟和预测,最终确定最佳的预测模型。借助建立的水产品品质预测模型,可以迅速而有效地预测和监控贮运过程中水产品的品质情况，并据此设计和评估水产品贮运过程的一系列技术参数。在今后的研究中，应尝试将更多的人工智能数学模型应用于水产品的品质预测中，同时将更多的水产品品质预测模型纳入计算机软件，并逐渐完善现有的微生物预测模型软件，以增加模型的实际应用功能，为水产品的贮运提供更多便利和参考价值。

[1] 夏文水. 大宗淡水鱼贮运保鲜与加工技术[M]. 北京: 中国农业出版社, 2014.

[2] Zhu S, Luo Y, Hong H, et al. Correlation between electrical conductivity of the gutted fish body and the quality of bighead carp (Aristichthysnobilis) heads stored at 0 and 3 °C[J]. Food Bioprocess Technol, 2013, 6(11): 3068-3075.

[3] 曹悦, 陆利霞, 熊晓辉. 食品货架期预测新技术进展[J]. 食品研究与开发, 2009, 30(5):165-168.

[4] Hong H, Luo Y, Zhu S, et al. Establishment of quality predictive models for bighead carp (Aristichthysnobilis) fillets during storage at different temperatures [J]. Int J Food Sci Technol, 2012, 47(3):488-494.

[5] 史波林, 赵镭, 支瑞聪. 基于品质衰变理论的食品货架期预测模型及其应用研究进展[J]. 食品科学, 2012, (21):345-350.

[6] Boekel M. Statistical aspects of kinetic modeling for food science problems [J]. J Food Sci, 1996, 61(3): 477-486.

[7] Liu X, Jiang Y, Shen S, et al. Comparison of arrhenius model and artificial neuronal network for the quality prediction of rainbow trout (Oncorhynchusmykiss) fillets during storage at different temperatures [J]. LWT - Food Sci Technol, 2015, 60(1):142-147.

[8] Yao L, Luo Y, Sun Y, et al. Establishment of kinetic models based on electrical conductivity and freshness indictors for the forecasting of crucian carp (Carassiuscarassius) freshness [J]. J Food Eng, 2011, 107(2):147-151.

[9] Zhang L, Li X, Lu W, et al. Quality predictive models of grass carp (Ctenopharyngodonidellus) at different temperatures during storage [J]. Food Contr, 2011, 22(8):1197-1202.

[10] Shi C, Lu H, Cui J, et al. Study on the predictive models of the quality of silver carp (Hypophthalmichthysmolitrix) fillets stored under variable temperature conditions [J]. J Food Process Pres, 2014, 38(1): 356-363.

[11] Bao Y, Zhou Z, Lu H, et al. Modelling quality changes in Songpu mirror carp (Cyprinuscarpio) fillets stored at chilled temperatures: comparison between Arrhenius model and log-logistic model [J]. Int J Food Sci Technol, 2013, 48(2):387-393.

[12] Dalgaard P. Qualitative and quantitative characterization of spoilage bacteria from packed fish[J]. Int J Food Microbiol, 1995, 26(3): 319-333.

[13] 杨宪时, 许钟, 肖琳琳. 水产食品特定腐败菌与货架期的预测和延长[J]. 水产学报, 2004, 28(1):106-111.

[14] Isabelle L, André L. Quantitative prediction of microbial behaviour during food processing using an integrated modelling approach: a review [J]. Int J Refrig, 2006, 29(6):968-984.

[15] Zwietering M H, Koos J T D, Hasenack B E, et al. Modeling of bacterial growth as a function of temperature.[J]. Appl Environ Microb, 1991, 57(4):1094-101.

[16] 崔正翠, 许钟, 杨宪时, 等. 大菱鲆腐败菌生长动力学研究和货架期预测 [J]. 海洋渔业, 2010, 32(4):454-460.

[17] 李学英, 杨宪时, 郭全友. 鲤鱼假单胞菌生长动力学研究和货架期预测 [J]. 食品与机械, 2011, 27(1):56-59.

[18] Dabadé D S, Azokpota P, Nout M J R, et al. Prediction of spoilage of tropical shrimp (Penaeusnotialis) under dynamic temperature regimes[J]. Int J Food Microbiol, 2015, 210(1):121-130.

[19] Mejlholm O, Gunvig A, Borggaard C, et al. Predicting growth rates and growth boundary ofListeriamonocytogenes-an international validation study with focus on processed and ready-to-eat meat and seafood [J]. Int J Food Microbiol, 2010, 141(3):137-150.

[20] Mejlholm O, Dalgaard P. Development and validation of an extensive growth and growth boundary model for psychrotolerantLactobacillusspp. in seafood and meat products [J]. Int J Food Microbiol, 2013, 167(2):244-260.

[21] García M R, Vilas C, Herrera J R, et al. Quality and shelf-life prediction for retail fresh Hake (Merlucciusmerluccius)[J]. Int J Food Microbiol, 2015, 208(2):65-74.

[22] Dalgaard P, Cowan B J, Heilmann, et al. The seafood spoilage and safety predictor (SSSP)[C]//Catholic University of Louvain. Proceedings of the 4th international conference in predictive modelling in foods. Louvain:Catholic University of Louvain, 2003: 258.

[23] Dalgaard P. Food spoilage and safety predictor (FSSP) software: annual report on zoonoses in denmark[R]. Denmark: Technical University of Denmark, 2013.

[24] 杨宪时, 许钟, 郭全友. 养殖鱼类货架期预测系统的设计与评估[J]. 农业工程学报, 2006, 22(8):129-134.

[25] Hong H, Luo Y, Zhu S, et al. Application of the general stability index method to predict quality deterioration in bighead carp (Aristichthysnobilis) heads during storage at different temperatures [J]. J Food Eng, 2012, 113:554-558.

[26] Bao Y, Luo Y, Zhang Y, et al. Application of the global stability index method to predict the quality deterioration of blunt-snout bream (Megalobramaamblycephala) during chilled storage [J]. Food Sci Biotechnol, 2013, 22(5):1-5.

[27] Zhu S, Luo Y, Feng L, et al. Establishment of kinetic models based on electrical conductivity and global stability index for predicting the quality of Allogynogenetic crucian carps (Carassiusauratusgibelio) during Chilling Storage [J]. J Food Process Pres, 2015, 39(2): 167-174.

[28] Gacula M C. The design of experiments for shelf life study [J]. J Food Sci, 2006, 40(2): 399-403.

[29] Gacula M C, Kubala J J. Statistical models for shelf life failures [J]. J Food Sci, 1975, 40(2): 404-409.

[30] Corradini M G, Peleg M. A model of non-isothermal degradation of nutrients, pigments and enzymes [J]. J Sci Food Agr, 2004, 84(3): 217-226.

[31] Barraza F A A. Kinetics of protein and textural changes in Atlantic salmon under frozen storage [J]. Food Chem, 2015, 182(1): 120-127.

[32] Wang H, Kong C, Li D, et al. Modeling quality changes in brined bream (Megalobramaamblycephala) fillets during storage: comparison of the arrhenius model, BP, and RBF neural network [J]. Food Bioprocess Technol,2015,8(12):2429-2443.

[33] Boekel M. Kinetic modeling of food quality: a critical review [J]. Compr Rev Food Sci F, 2008, 7(1):144-158.

Developments of quality prediction techniques in storage and transportation ofaquatic products

LIU Xiaochang, LUO Yongkang*

(College of Food Science and Nutritional Engineering, China Agricultural University, Beijing 100083)

Aquatic products quality degrades rapidly during storage and transportation as a consequence of biochemical and microbial breakdown mechanisms. Traditional quality detection methods of aquatic products are time-consuming and tedious. As a result, they are not suitable for real-time monitoring during commodity circulation. Quality prediction technology, based on mathematical models to simulate and predict aquatic products quality, can realize real-time monitoring of aquatic products quality. This paper reviewed and compared several prediction models which have been used in aquatic products, such as kinetic models, microbial growth prediction models, mathematical models based on global stability index and artificial intelligence, with a view to providing useful information for the development and improvement of prediction techniques in aquatic products. [Chinese Fishery Quality and Standards, 2016, 6(2):1-6]

aquatic product; prediction technique; storage; model

LUO Yongkang, luoyongkang@263.net

2015-08-01：；接收日期：2015-10-09

现代农业产业技术体系建设专项资金资助(CARS-46)；北京市自然科学基金资助项目(6152017)；国家科技支撑项目(2015BAD17B00)

刘晓畅(1990-)，女，博士，研究方向为食品贮藏与保鲜，lxc_cau@163.com

：罗永康，教授，研究方向为水产品贮藏与加工，luoyongkang@263.net

S94

：A

：2095-1833(2016)02-0001-06