一类分数阶区间系统的静态量化反馈镇定分析

高 扬，赵 微，卢树强

(大庆师范大学 教师教育学院，黑龙江 大庆 163712)

一类分数阶区间系统的静态量化反馈镇定分析

高 扬，赵 微，卢树强

(大庆师范大学 教师教育学院，黑龙江 大庆 163712)

首先在Caputo分数阶导数意义下，针对导数阶数在0到1开区间的一类分数阶区间系统，探讨了系统的量化反馈镇定问题。采用扇形界(sector bound)思想研究该系统的量化反馈控制器设计。通过设计适合的静态量化反馈控制器，得到分数阶区间系统Mittag-Leffler 镇定定理。其次，利用Lyapunov直接方法和Mittag-Leffler型稳定理论，证明了分数阶区间系统的状态量化反馈镇定和输出量化反馈镇定定理。

Caputo型导数；分数阶导数；量化器；Mittag-Leffler 型稳定

0 引言

分数阶微积分的历史可以追述到300多年前，但它的兴起却是在最近的50年间。分数阶微积分的概念起源于1695年，Gottfried Wilhelm Leibniz 给Marquis L'Hopital的信件中提到了1/2阶导数的意义及有关问题。随后，分数阶微积分受到了许多著名数学家的关注。

稳定性理论作为控制理论的基石，得到了众多学者的关注。对分数阶微分方程稳定性的研究自然也是分数阶微分方程的重要部分。分数阶微分方程的稳定性研究成果丰富，但是基于Lyapunov函数的研究结果还很少。另外现有稳定、镇定方面成果多数仅仅考虑渐近稳定方面。特别是分数阶线性系统方面，虽然线性矩阵不等式方法广泛应用，但是多数是基于渐近稳定问题进行分析。2009年文献[1]提出了Mittag-Leffler稳定概念。此种稳定性可以看成整数阶系统的指数稳定性的推广。作者建立了分数阶系统实现Mittag_Leffler稳定的Lyapunov定理，并建立了分数阶系统的比较原理。2014年文献[2]证明了一个不等式，探讨了Caputo导数意义下的分数阶微分系统的Lyapunov函数构造的问题。该不等式的建立使得二次Lyapunov函数的构造可以实现。2015年文献[3]中，作者利用了二次Lyapunov函数分数阶导数的不等式，来探讨分数阶非线性系统的稳定性。该文献最重要的贡献是把整数阶系统常用的线性矩阵不等式方法推广到分数阶非线性系统中。通过Laplace变换，利用终值定理来求出分数阶微分方程的稳定条件的做法很成熟[4-7]。但是通过构造Lyapunov函数，来得出方程的Mittag-Leffler稳定和镇定条件的方法还处于初级阶段。

众所周知通过构造Lyapunov函数，设计系统量化反馈镇定控制器在整数阶系统中广泛应用。1956年， Kalman研究了样本数据系统的量化效果，并指出反馈系统会出现极限环和混沌行为[8]。Fu Mingyue用扇形界(sector bound)思想研究了离散线性系统的量化反馈控制[9]。该文献提出的量化器可以看成取值为可数点集并且是静态的。由Francesca Ceragioli进一步推广得到一般的仿射非线性系统[10]。在非线性系统中量化反馈控制也得到了广泛研究。比如，D．Liberzon的动态量化器[11]。 在解决非线性系统的量化反馈镇定问题时，小增益定理起到了重要作用。关于这方面的近期工作Jiang ZP进行了详细论述[11]。

把整数阶线性系统的静态量化反馈镇定控制设计推广到分数阶线性系统情况是一个既有理论研究意义，又有实用价值的课题。但是在分数阶系统中基于Lyapunov理论研究量化反馈镇定的研究成果很少见到，特别是基于Lyapunov理论研究量化反馈Mittag-Leffler型镇定的研究成果更是未见到。本文在Caputo分数阶导数意义下，针对导数阶数在0到1开区间的一类分数阶区间系统，首先建立此类系统的Mittag-Leffler型镇定定理。之后用扇形界(sector bound)思想研究该系统实现反馈镇定的量化控制器设计。通过Lyapunov直接方法，得到了分数阶区间系统的状态量化反馈镇定和输出量化反馈镇定定理。

1 预备知识

考虑分数阶非线性系统：

(1.1)

D表示Caputo分数阶算子，α∈(0,1)。f：R×Rm→Rn为局部Lipschtiz的。x(t)∈Rn表示系统在t∈R+时刻的状态。并假设f(0,0)=0。以下给出系统(1.1)Mittag-Leffler稳定的定义。

定义1.1[1]上述分数阶系统(1.1)的解是Mittag-Leffler稳定的，若

||x(t)||≤{m[x(t0)]Eα(-λ(t-t0)α)}b

其中t0为初始时刻，α∈(0,1)，λ>0,b>0,m(0)=0,m(x)≥0，函数m(x)是局部Lipschtiz的。

引理1.1设x(t)∈Rn是一个连续可导函数，矩阵P正定。则对任意时间t≥t0有

对任意α∈(0,1)成立[2-3]。

定义1.2[9]一个量化器被称为是对数型的(logarithmic)，若它拥有如下形式

U={±u(i):u(i)=ρiu(0),i=±1,±2,…}∪{±u(0)}∪{0}。

这里0<ρ<1,u(0)>0。此时，量化器f可定义为：

对于一般的多输入系统(例如，u∈Rm)，参看文献[9]给出了此种类型量化器的定义。即

f(v)=diag{f1(v1),f2(v2),L,fm(vm)}

这里vj是v的第j个分量，0<ρj<1。可以定义ρ=[ρ1,ρ2,L,ρm]。每个fj都是对数型的(logarithmic)量化器。定义Δ(t)=diag{Δ1(t),L,Δn(t)}，这里Δj(t):R→[-δj,δj]，要求∀Δj0∈[-δj,δj]，∃vj0≠0,s.tΔj0(vj0)=Δ0。则系统输入为u=Kx时，量化后可变化为

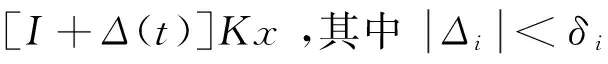
2 主要结论

考虑带有Caputo导数的分数阶区间系统：

(2.1)

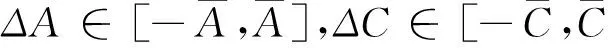
2.1 基于状态反馈的量化器设计

证明：取Lyapunov函数为V(x(t))=xTPx，利用引理1.1-1.3的结论并经计算得到

≤2xTP(A + Δ A + BK)x

= 2xTP(A + BK)x + 2xTPΔ Ax

= xTP(A + BK)x + xT(A + BK)TPx + 2xTPΔ Ax

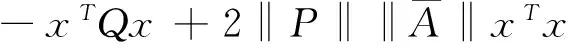
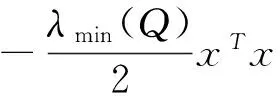
总的看来，GC-MS在白酒塑化剂的测定中，具有较好的定量效果，前提是做好样品的前处理，避免前处理使用的试剂等进入白酒而造成干扰。

sαw(s)-w(0)sα-1+M(s)=-βw(s)

其中w(s)为w(t)的Laplace变换，M(s)为M(t)的Laplace变换。再用逆Laplace变换有 w(t)=w(0)Eα(-βtα)-M(t)*[tα-1Eα,α(-βtα)]≤w(0)Eα(-βtα)。进而知系统(2.1)解是Mittag-Leffler稳定的。

综上，系统(2.1)通过采取u=Kx的状态反馈实现反馈镇定。

下一步我们建立系统(2.1)的量化反馈镇定定理。

定理2.2若下列条件成立：

(1)存在正定矩阵P,Q及矩阵K使等式成立：P(A+BK)+(A+BK)TP=-Q，

则系统(2.1)可以采用对数型的量化器实现量化反馈镇定。其中u=f(Kx)。

证明：由定理2.1知状态反馈u=Kx可以实现系统(2.1)镇定，进而取对数性量化反馈为u=f(Kx)。

由对数性量化器的性质有u=f(Kx)=(I+Δ(t))Kx。进一步取Lyapunov函数为V(x(t))=xTPx。利用引理1.1-1.3的结论并经计算得到

≤2xTP(A + Δ A + (I + Δ (t))BK)x

= 2xTP(A + BK)x + 2xTPΔ Ax + 2xTPΔ (t)BKx

= xTP(A + BK)x + xT(A + BK)TPx + 2xTPΔ Ax + 2xTPΔ (t)BKx

2.2基于输出反馈的量化器设计

我们首先建立系统(2.1)的静态输出反馈镇定定理。

定理2.3 若存在正定矩阵P,Q及矩阵K使得下面等式成立：P(A+BKC)+(A+BKC)TP=-Q，

进而有如下量化反馈设计定理成立。

定理2.4若下列条件成立：

(1)存在正定矩阵P，Q及矩阵K使等式成立：P(A+BKC)+(A+BKC)TP=-Q，

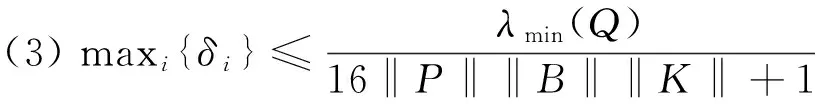
则系统(2.1)可以采用对数型的量化器实现量化反馈镇定，其中u=f(KCx)。

3 实例

为了展示定理2.2的应用性，我们举一个例子。

4 结 论

本文在Caputo分数阶导数意义下，针对导数阶数在0到1开区间的一类分数阶区间线性系统，用扇形界(sector bound)思想研究该系统实现反馈镇定的量化控制器设计。通过Lyapunov直接方法，得到了分数阶区间线性系统的状态量化反馈镇定和静态输出量化反馈镇定定理。创新之处在于把静态量化器应用于分数阶区间线性系统。另外，利用Lyapunov直接方法建立分数阶区间线性系统的Mittag-Leffler型稳定Lyapunov定理也是本文一大创新点，下一步我们将继续探索带有分数阶非线性系统的量化反馈镇定问题。

[1] Li Y，Chen YQ，Podlubny I．Mittag-Leffler stability of fractional order nonlinear dynamic systems[J]．Automatica，2009，45(8)：1965-1969．

[2] Aguila-Camacho N，Duarte-Mermoud MA，Gallegos JA．Lyapunov functions for fractional order systems[J]．Communications in Nonlinear Science and Numerical Simulation，2014，19(9)：2951-2957．

[3] Liu S，Jiang W，Li XY，Zhou XF．Lyapunov stability analysis of fractional nonlinear systems[J]．Applied Mathematics Letters，2016，51：13-19．

[4] Matignon D．Stability results for fractional differential equations with applications to control processing[J]．Computational engineering in systems applications，1996，2：963-968．

[5] Tavazoei M S，Haeri M．A note on the stability of fractional order systems[J]．Mathematics and Computers in Simulation，2009，79(5)：1576．

[6] Lu JG，Chen G．Robust stability and stabilization of fractional-order interval systems:an LMI approach[J]．IEEE Transactions on Automatic Control，2009，54(6)：1294-1299．

[7] Lu JG，Chen YQ．Robust Stability and Stabilization of Fractional-Order Interval Systems with the Fractional Order：The Case[J]．IEEE Transactions on Automatic Control，2010，55(1)：152-158．

[8] Kalman RE．Nonlinear aspects of sampled-data control systems[B]．Proc Symp．Nonlinear Circuit Theory，vol VII，Brooklyn， NY，1956．

[9] Fu MY，and Xie LH，The sector Bound Approach to quantized feedback control[J]．IEEE Transactions on Automatic Control，2005，50(11)：1698-1710．

[10] Ceragioli F，Persis CD．Discontinuous stabilization of nonlinear systems:quantized and switching controls[J]．Systems and Control Letters，2007，56：461-473．

[11] Jiang ZP，Liu TF．A Survey of Recent Results in Quantized and Event-based Nonlinear Control[J]．International Journal of Automation and Computing，2015，12 (5)：455-466．

[12] Li Y，Chen YQ，Podlubny I．Stability of fractional-order nonlinear dynamic systems：Lyapunov direct method and generalized Mittag-Leffler stability[J]．Computers& Mathematics with Applications，2010，59(5)：1810-1821．

[13] Mao X，Lam J，Xu S，et al．Razumikhin method and exponential stability of hybrid stochastic delay interval systems[J]．Journal of Mathematical Analysis & Applications，2006，314(1)：45-66．

[14] 吴丁娟，陈东彦．一类不确定性Lurie控制系统的鲁棒绝对稳定判据[J]．哈尔滨理工大学学报，2005，10(1)：150-152．

[15] 游文虎，王茂，赵建妮，等．一种新的分数阶三维自治混沌系统[J]．哈尔滨理工大学学报，2013，18(4)：7-11．

[责任编辑：崔海瑛]

Static Quantized Feedback Stabilization Analysis for One Class of the Fractional Order Interval System

GAO Yang, ZHAO Wei, LU Shu-qiang

(1. Teaching Education College of Daqing Normal University , Daqing 163712,Heilongjiang China)

Firstly, the quantized feedback stabilization problem is discussed for the fractional order interval system with Caputo-type fractional derivative where the order of the derivative is in the interval(0,1). The sector bound method is used to study the quantized feedback stabilization controller's designing for the system. The fractional order interval system's Mittag-Leffler type stabilization theorems are obtained by designing the reasonable static quantized feedback stabilization controller. Secondly, the state quantized feedback stabilization and output quantized feedback stabilization Lyapunov theorems for the fractional order interval system are shown by using the Lyapunov directed method and Mittag-Leffler type stability theory. Finally, an example is provided to illustrate the main theorem.

Caputo type derivative; Fractional order derivative; Quantizer; Mittag-Leffler type stability.

高扬(1979-)，男，黑龙江大庆人，副教授，从事网络控制系统方向研究。

大庆市科技计划项目“几类分数阶微分方程稳定性与应用研究”(szdfy-2015-63)。

O231.1

A

2095-0063(2016)06-0049-05

2016-03-16

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.06.011