推广的潜在索赔风险模型的破产概率

郭 航， 金燕生， 张 衡

(燕山大学 理学院 河北 秦皇岛 066004)



推广的潜在索赔风险模型的破产概率

郭 航， 金燕生， 张 衡

(燕山大学 理学院 河北 秦皇岛 066004)

改进了一类潜在索赔风险模型，把保费由固定变为取多个值的随机变量，将索赔额序列由独立推广到广义负相依，在假设索赔额分布为L∩D族情况下，得到了有限时间破产概率的一个渐近等价式.

重尾分布； 破产概率； 广义负相依； 潜在索赔

0 引言

(1)

针对模型(1)，文献[7]研究了索赔额为D族且负相关下的精细大偏差,文献[8]研究了索赔额为ERV族,{N(t),t≥0}为复合二项过程的精细大偏差和有限时间破产概率，文献[9]研究了更新计数过程索赔额负相依下的破产渐近表达式，文献[10]将[9]中的索赔额推广到S族，但索赔额分布重新变为独立的.

1 模型和引理

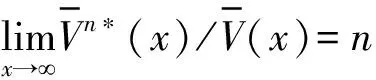
定义2 称随机变量ξ1,ξ2,…,ξn是下广义负相依的，若存在M>0，使得对所有xi,i=1,2,…,n有

(2)

称随机变量ξ1,ξ2,…,ξn是上广义负相依的，若存在M>0使得对所有的xi,i=1,2,…,n有

(3)

称随机变量ξ1,ξ2，…，ξn是广义负相依的，若同时满足式(2)和(3)，若M=1,则就是负相依的定义.

有了上述定义，在模型(1)基础上，假设第k个投保人保费为Fk，文献[4-8]中Fk≡μ(1+ρ)，将固定的保费由μ(1+ρ)推广到离散随机变量L，其取有限个有界值0μ，显然模型(1)是在m=1时的特殊情况，此外再假设索赔额{Xk,k=1,2…}是广义负相依的且分布属于L∩D族，因此新的模型就变为,,定义T时刻的破产概率为

对于新模型有如下说明：(A1) {Fk∶k≥1},{Ik∶k≥1},{Xk∶k≥1},{N(t)∶t≥0}之间是相互独立的,(A2) {Ik∶k≥1}之间是相互独立的，存在0<θ<+使得成立,(A3) {N(t)∶t≥0}具有有限的均值函数m(t)=E[N(t)].

引理2 对于任意的正整数n，在引理1条件下有

(4)

证明 当n=1时(4)式显然成立，以下证n≥2时成立.取1≤i≠j≤n，又由引理1得{IkXk:K≥1}是广义负相依的，故P(IiXi>x,IjXj>x)≤MP(IiXi>x)P(IjXj>x)=o(P(I1X1>x)).因此

(5)

(6)

(7)

又Xk的分布属于L∩D族，由D族定义可得∃x0>0，当x>x0时，存在常数c0有，

P(X1>x/n)≤c0P(X1>x).

(8)

(9)

由(9)和(5)式可得(4)式成立，证毕.

2 主要成果

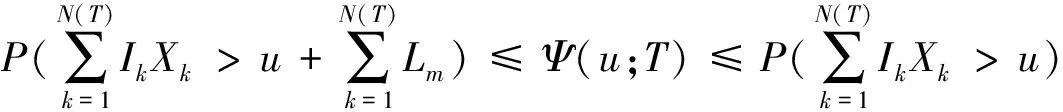
(10)

考察(10)式第二个不等号，对于任意的正整数B，t∈(0,T]有

(11)

对于I2(u,t,B)，由条件(A2)及Xk为L∩D族，由文献[4]中的思想可知，存在正的常数p，h，C，H，当u≥H时，有

由N(T)具有有限均值，根据文献[14]知,存在h>0，对任意的T≥0都有E[ehN(T)]<，又为B

(12)

对于I1(u,t,B)，构造

(13)

(14)

又对∀u有

(15)

综合式(13)～(15)得

(16)

又由(11)～(12)式及(7)式可得

(17)

由引理1知,{IkXk-Lm:K≥1}是END的且分布族支撑在[-Lm,+)属于L∩D族，故与(17)式的证明过程相同，可得(t)]. 又由L族定义可得证毕.

3 结论

本文推广了一类基于潜在索赔的风险模型，相比模型(1),其更符合保险公司实际经营状况，在索赔分布族为L∩D族情况下，得到了一个有限时间破产概率的渐近等价式，该等价式可以在一定程度上评估保险公司的风险情况，对保险公司的风险控制有一定的借鉴意义.

[1] EMBRECHTS P,KIÜPPELBERG C,MIKOSCH T.Modelling extremal events for insurance and finance [M].Berlin:Springer,1997.

[2] 刘超,王永茂,颜玲,等.带干扰的多险种二项风险模型的破产概率[J].郑州大学学报(理学版),2012,44(1):51-54.

[3] 王汉芹,金燕生,刘媛媛.险种间的相关性对调节系数的影响[J].郑州大学学报(理学版),2013,45(3):24-27.

[4] TANG Q.Asymptotic ruin probabilities of the renewal model with constant interest force and regular variation[J].Asia-paciffc microanalysis association,1994,1(1):1-5.

[5] YANG Y, LIN J G, GAO Q W. Asymptotics for the in nite-time absolute ruin probabilities in time-dependent renewal risk models[J].Scientia sinica, 2013, 43(2): 173-184.

[6] KAI W,TANG Q, YANG J,et al.Precise large deviations for the prospective-loss process[J]. Journal of applied probability, 2003, 40(2):391-400.

[7] WANG Y B,WANG Y.Precise large deviations for sums of negative associated random variables with common dominatedly varying tails[J].Acta mathematica sinica：English series,2006,22(6):1725-1734.

[8] 马学敏,胡亦钧.复合二项过程风险模型的精细大偏差及有限时间破产概率[J].数学学报,2008,51(6):1119-1130.

[9] 肖鸿民,刘建霞.带负相依重尾潜在索赔额的风险模型的有限时间破产概[J].山东大学学报(理学版),2011,46(9):117-121.

[10] 肖鸿民,赵婕,宋国龙.具有潜在索赔的风险模型在重尾赔付下的极限性质[J].西北师范大学学报(自然科学版),2015,51(2):9-11.

[11] LI L.Precise large deviations for dependent random variables with heavy tails[J].Statistics probability letters, 2009,79(9): 1290-1298.

[12] CHEN Y.The strong law of large numbers for extended negatively dependent random variables[J].Journal of applied probability, 2010,47(4):908-922.

[13] 杨洋,冯翠莲,张燕.基于相依风险模型破产概率的渐近估计及其实证分析[J].数理统计与管理,2013,32(1):28-34.

[14] HAO X,TANG Q.A uniform asymptotic estimate for discounted aggregate claims with subexponential tails[J].Insurance mathematics and economic, 2008,43(1):116-120.

(责任编辑：方惠敏)

Ruin Probability for an Extended Prospective-claim Risk Model

GUO Hang JIN Yansheng ZHANG Heng

(CollegeofScience,YanshanUniversity,Qinhuangdao066004,China)

An improved potential claim risk model was proposed,in which the fixed premium was replaced by a random variable with multiple values and the claim sequence’s independence was replaced by extended negatively dependence.Under the claim amount distribution belongs to classL∩D,an asymptotical expression of the finite-time ruin probability was derived.

heavy-tailed distribution; ruin probability; extended negatively dependence; prospective-claim

2016-05-28

郭航(1992—)，男，河北邢台人，硕士研究生，主要从事保险精算研究，E-mail:singdax@sina.com;通讯作者:金燕生(1960—)，男，黑龙江齐齐哈尔人，副教授，主要从事保险精算研究,E-mail:jys1960@ysu.edu.cn.

郭航,金燕生,张衡.推广的潜在索赔风险模型的破产概率[J].郑州大学学报(理学版)，2016，48(4)：15-19．

O2116

A

1671-6841(2016)04-0015-05

10.13705/j.issn.1671-6841.2016623