数学教学中如何促进学生的理解

郭文江+付杰

摘要：理解是指通过个体思维逐步认识事物的内在联系及本质规律。学生必须在理解知识的过程中掌握知识、提高能力。为实现这一目标，要求教师在教学中采用适合学生的直观教学、运用变式、比较分析、归类列表、剖析错误、激情引趣等各种策略和方式，让学生在民主、和谐的氛围中学习数学，通过感悟和理解，探索数学奥秘。

关键词：小学数学；直观教学；显示本质；揭示异同；归类列表

所谓理解是指通过个体思维逐步认识事物的内在联系及本质规律。学生必须在理解知识的过程中掌握知识、提高能力。为强化数学知识的理解可采取如下六条措施。

一、直观教学，丰富感知

在小学数学教学中，如果能合理地运用直观教学，创设良好的学习情境，就能为学生理解抽象的数学知识提供丰富的感性材料，减少学生在学习中的困难，调动学生学习的积极性，提高学生的思维能力。直观具体的实物、模具、图像生动形象，教师富有感染力的语言并借助表情、手势、动作及形象化的描述都能使抽象的问题直观化、简单形象化，便于学生理解和掌握知识。如对一年级的学生，教师可以通过数小棒，自制“小花朵”、“五星”、“小动物”等实物图形让学生观察、拼摆、感知数的意义。再如，高年级学生学习轴对称图形，用硬纸片剪成等腰三角形、等边三角形、长方形、正方形、圆、扇形等教具、学具。通过对折，反复试验，理解对称图形和对称轴的概念。

二、运用变式、显示本质

由于学生年龄小，阅历浅，思维更具形象性，抽象思维能力不强。教学时如果不断重复同一类型、同一特征的题，学生很容易把题目某些特征与算法联系起来，形成思维定势，看到“共”就“加”、看到“少”就“减”、看到“平均”就“除”。要克服学生这种静止孤立思考问题习惯的方法之一就是运用变式。所谓变式是指提供给学生各种类型的问题不断变换形式，展示本质特征，启发学生思维，提高应变能力。如教学“直角三角形”时，教师可在讲解一般形式的直角三角形外，再出现其他各种位置、各种形状的直角三角形来说明虽然形式不一，但本质属性不变。再如，学习“三角形内角和是180度”这一性质时，教师首先出示一个等腰三角形进行验证，然后沿高对称一分为二成两个完全一样的小三角形，提问学生：“每个小三角形的内角和是原来大三角形内角和的一半吗？”从而使学生理解“任何三角形的内角和都是180度”的普遍规律。

三、比较分析、揭示异同

学生容易把相似的概念相混淆，这就要求教师引导学生通过对同类、异类的事物分析比较，找出异同，更好地理解知识，把握本质。如，整除一章把如下六个概念对比分析、理解：约数一公约数一最大公约数；倍数一公倍数一最小公倍数，最大公约数与最小公倍数的相同点是都可用短除法求，都可以用几个数的公约数去除；不同点是在用短除法去求时，最大公约数要求除数必须是所有数的公约数，最后积（最大公约数）只是除数相乘，不乘商；而最小公倍数的除数不一定是几个数的公约数，最后积（最小公倍数）把商与除数连乘起来。

四、归类列表，力求系统

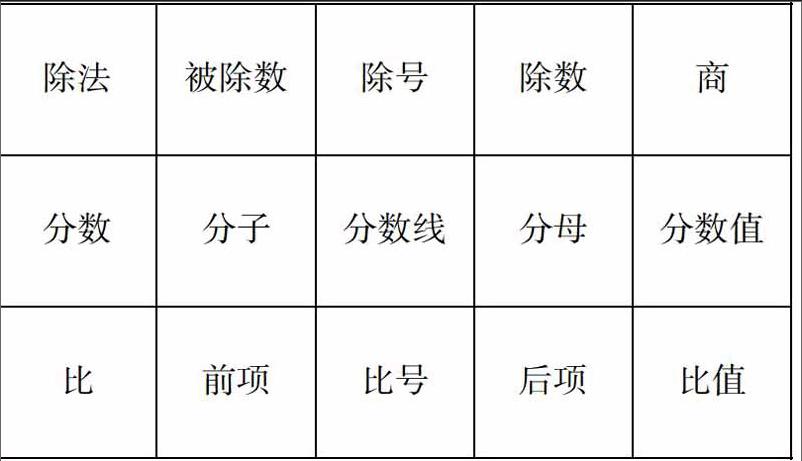
知识之间既有区别，又有联系，它是按一定的规律和次序组成的一个体系。教师只有在循序渐进的基础上传授知识，又善于总结、归纳知识，才能使学生获得知识系统化、完整化，才能真正地理解巩固知识。如，六年级复习阶段，有关除法、分数、比方面的知识，我绘制了如下表格，学生看后一目了然。

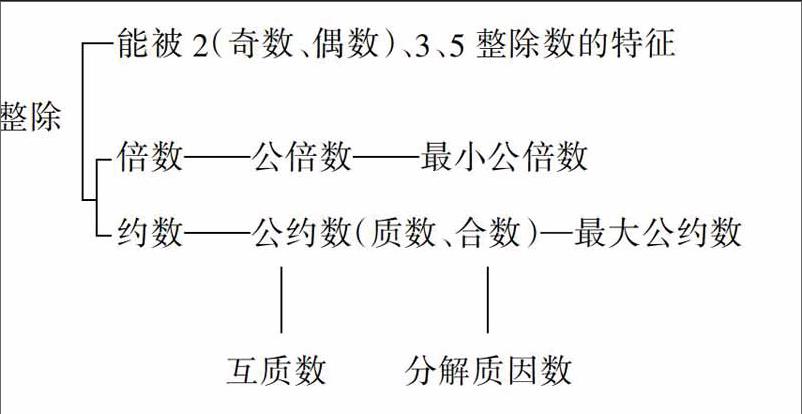
再如，五年级整除引出有关概念知识图表：

五、剖析错误辨非明理

通过对错题的剖析，帮助学生找出原因，采取合理可行的方法解决，做到以正改错。这样不仅有利于学生知错改错，而且更有利于培养学生思维的缜密性和严谨性。我多采用学生作业中出现的有代表性的错题，通过生生互动交流，教师归纳指正，增强学生的理解能力。

六、激情引趣晓之以理

心理学家认为，兴趣、情趣等非智力因素对智力因素起着重要作用。良好的心境、最佳的学习状态能驱动学生积极思考、探索，有利于学生对知识的理解和掌握。因此，教师要创设良好的课堂氛围、和谐民主的学习环境，根据学生年龄特征，多采用喜闻乐见的形式激情引趣，使学生产生积极向上的精神和强烈的求知欲，在学中乐，乐中学，教学效果才能升华。

总之，促进学生理解的措施还有很多，教师在教学中应根据教材内容、学生实际情况因材施教，有针对性地采取一种或几种措施，引导学生理解，为学好数学打下良好的基础。