大跨径自锚式悬索桥主缆的线形计算及误差分析

杨恒，李元松，祁超，周小龙

武汉工程大学资源与土木工程学院，湖北武汉430074

大跨径自锚式悬索桥主缆的线形计算及误差分析

杨恒，李元松*，祁超，周小龙

武汉工程大学资源与土木工程学院，湖北武汉430074

针对自锚式悬索桥的主缆线形在施工过程中的变化特性，自编分段悬链线法和抛物线法程序实现了大跨径自锚式悬索桥主缆线形、空缆线形、各节段无应力长度、吊点坐标和索鞍预偏量等几何特征参数的精确计算；结合工程实例，对自编程序与Midas civil软件计算结果进行了比较分析.结果表明：与有限单元法相比，分段悬链线法计算得到的索鞍预偏量相对误差为11.3%，抛物线法计算得到的索鞍预偏量相对误差为23%.在施工中，分段悬链线法和抛物线法计算结果需要反复修正迭代以综合确定主缆线形.

自锚式悬索桥；主缆线形；分段悬链线法；抛物线法

1 引言

自锚式悬索桥因其造型新颖、跨越能力强、对地质条件要求低等特点，现已成为大、中跨径桥梁中具有较强竞争力的一种桥型，尤其是在软土地区和城市景观桥梁中，自锚式悬索桥越来越受到青睐［1-3］.随着国民经济和交通事业的快速发展，人们审美需求的不断提高，桥梁的跨越能力和靓丽外观逐渐占据重要地位，相应地伴随跨度的不断增大，桥梁的受力与变形特性更加复杂，其中几何非线性特征也愈显突出［4］.精确计算自锚式悬索桥的成桥线形与施工过程中的变化特性已成为该类桥梁设计与施工控制的关键技术问题，而主缆线形又是成桥线形的决定因素之一.

本文针对柔性结构的受力特点，基于静力平衡理论，详细讨论了主缆线形的计算公式与参数取值方法，自编Fortran程序实现了自锚式悬索桥主缆线形的精确计算，结合工程实例，给出自编程序与Midas civil软件计算结果，并进行了比较分析.

2 计算方法

2.1 基本平衡方程

现代大跨度悬索桥的主缆一般由钢丝集束而成，抗弯刚度很小，可按完全柔性处理.如图1所示，对于固定于A、B两端，受均布荷载w作用的索段，基本假定如下［5］：

1）柔索仅能承受拉力而不能承受弯矩；

2）成桥时吊杆为竖直方向；

3）索的横截面在荷载作用下不发生变化.

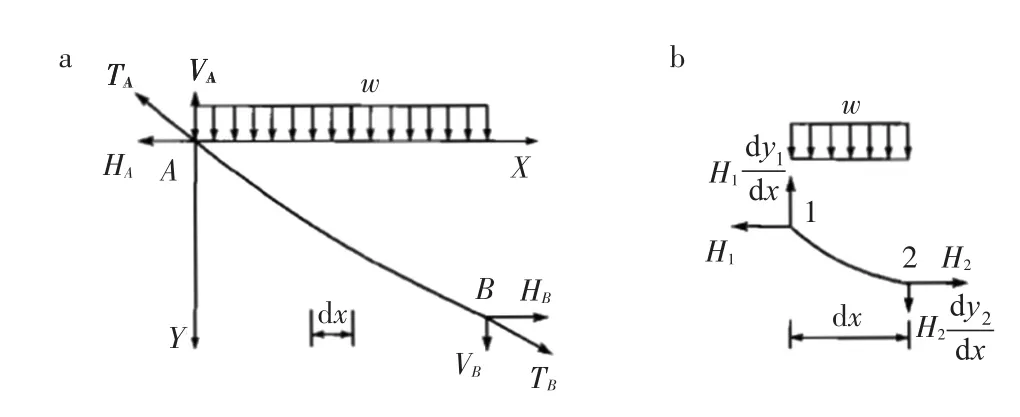
图1 均布荷载作用下索段力学模型（a）索段AB和（b）微索段1-2Fig.1Mechanical model of cable segments under uniform load（a）segment of cable AB and（b）micro-segment of cable 1-2

对于长度为dx的曲线段1和曲线段2，由力的平衡条件，得单边悬索的基本平衡方程［6-7］：

式（1）中：H为主缆拉力的水平分量，ω为均布荷载集度.

按荷载沿水平方向均匀分布或沿主缆长度均匀分布假设，式（1）的解有抛物线和悬链线2种.

2.2 抛物线法

抛物线法［8-9］假定主缆自重qc和桥面荷载qb沿跨长均匀分布，ω=qc+qb，如图2所示.

2.2.1 成桥主缆线形

基本平衡方程（1）的解为：

根据边界条件可求得主缆线形方程.

对两端等高的主缆、中跨：

图2 抛物线法主缆受力模式Fig.2Force model of main cable by parabola method

式（3）和式（4）中L1、L2、f1、h的定义见图2.

2.2.2 成桥状态索长

分别将式（3）、式（4）对弧长积分可得各节段变形后的索长［10］：

中跨的弹性伸长量：

边跨的弹性伸长量：

2.2.3 空缆线形和索鞍预偏量

设索鞍预偏量为d，空缆状态的水平分力为H#.主缆中跨、边跨跨度分别为：

中跨、边跨矢高分别为：

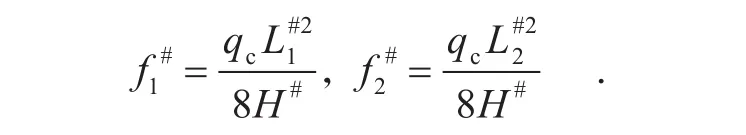
将上述几何参数分别代入式（5）～式（7）中，可以得空缆状态各节段的无应力长度.

由于预偏量d和水平力H#均为未知量，不能直接求出定解，根据各跨主缆在成桥恒载状态和空缆状态下的无应力索长均应相等，经迭代可求得空缆状态d和H#的解.

同理，根据吊杆间各索段的无应力长度不变原则，可依次迭代计算出各吊点的纵桥向坐标，代入空缆线形方程，从而求出空缆线形.

2.3 多段悬链线法

多段悬链线法的主缆受力如图3所示，假设主缆自重qc沿主缆均匀分布，桥面恒载qb转化为吊杆集中力Pi.此时平衡微分方程为［11-12］：

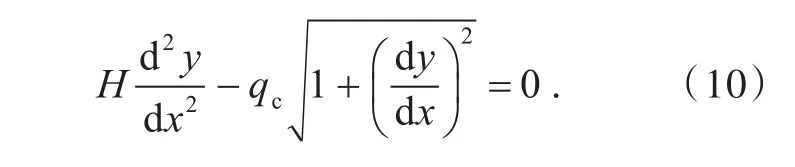
图3 多段悬链线法的主缆受力图示Fig.3Force diagram of main cable by segmented catenary method

2.3.1 成桥恒载状态对第i段进行受力分析，微分方程（10）的解为［13-15］：

第i段主缆的高度：

第i段主缆的索长：

忽略主缆弹性模量随应力大小的变化，设主缆的弹性模量为Ec，截面积为Ac，则第i段索的弹性伸长量为：

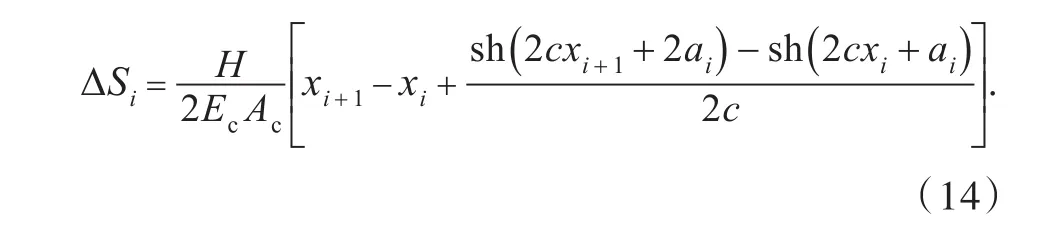
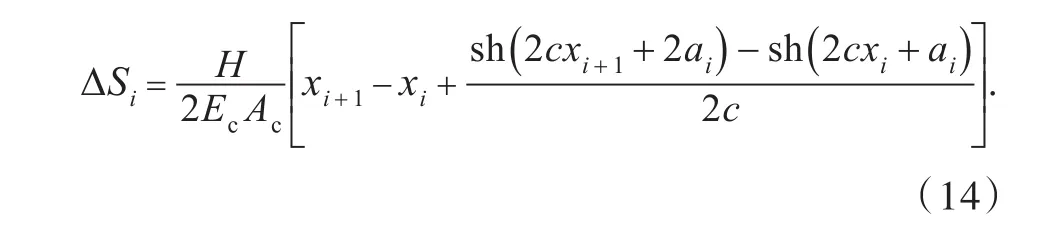
2.3.2 空缆状态

2.3.2.1 索鞍预偏量

设索鞍预偏量为d#，空缆状态主缆水平力为H#，主缆的中跨、边跨跨度分别为

根据各跨主缆在成桥恒载和空缆状态下的无应力索长相等的条件进行迭代求解.此时，求解d和H#.

2.3.2.2 主缆线形

以主缆状态下的中跨任意第i段主缆为例，设左右两吊点的坐标分别为(xi'yi)和(xi+1'yi+1).

有应力索长为：

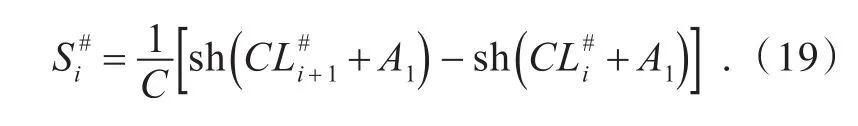
弹性伸长量为：

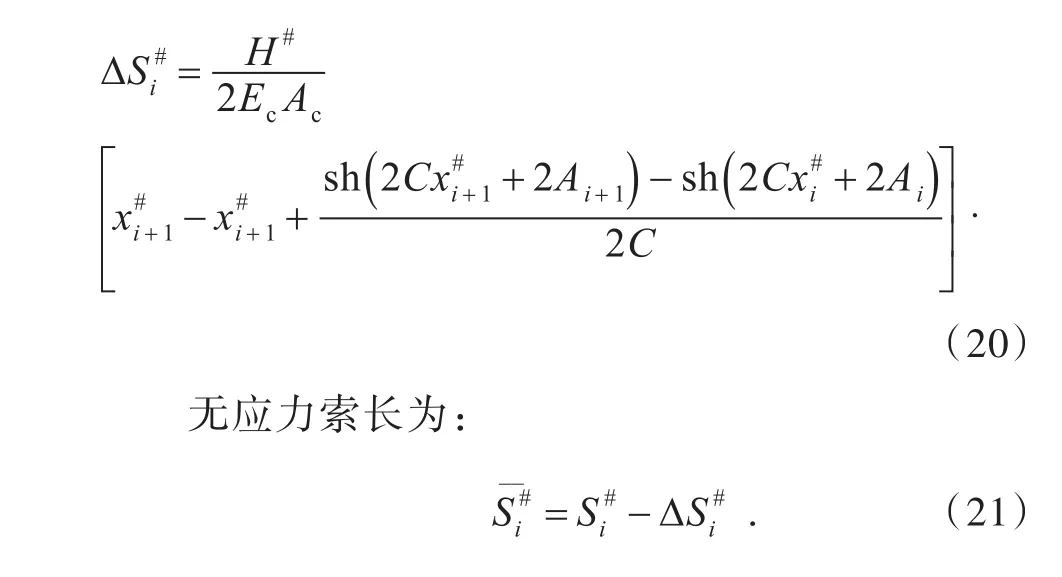
根据成桥和空缆两种状态下，吊杆之间各段的无应力索长相等的原则进行迭代运算.在已知

xi的基础上，求得各吊点的纵桥向坐标xi+1，将

xi+1代入悬链线方程即可得各吊点的空缆状态坐标，从而求得空缆线形.

2.3.3 计算流程及程序实现归纳前述各工况的计算公式，形成如图4所示计算流程，并自编Fortran程序.

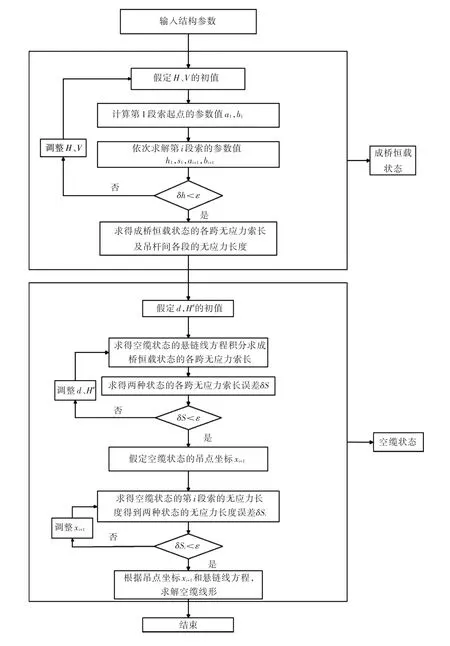
图4 多段悬链线法计算流程图Fig.4Flowchart of calculation for main cable by segmented catenary method

3 工程实例

3.1 基本数据

某桥为双索面钢箱加劲梁自锚式悬索桥，立面布置如图5所示.桥梁基本参数：中跨吊杆间距L1=600 m（40×15 m），f1=60 m，边跨吊杆间距L2=195 m（11×15 m+30 m），高度h=65.2 m；单根主缆截面Ac=0.257 8 m2，Ec＝2.0×105MPa，单位长度重qc=20.436kN/m；单根吊杆截面Ad=5.439×10-3m2，Ed=2.0×105MPa，单位长度重qd=0.424 kN/m；加劲梁截面Ab=3.066 7 m2，Eb=2.06×105MPa，单位长度重qb=165.2 kN/m（加二期恒载）.

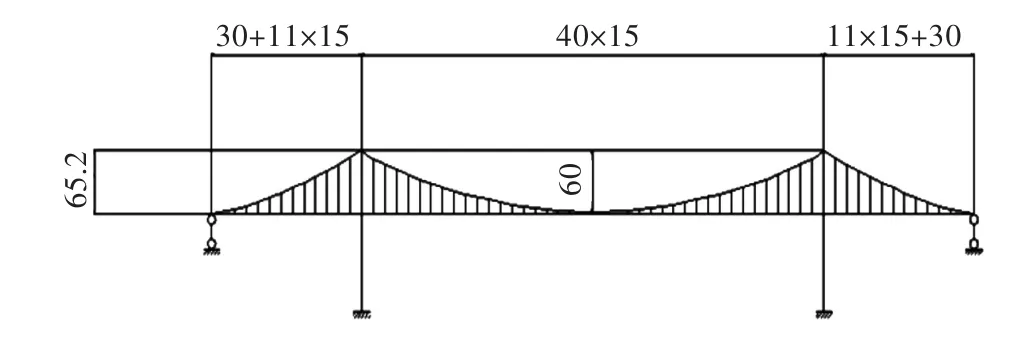
图5 自锚式悬索桥结构体系简图（单位：m）Fig.5Structural profile of self-anchored suspension bridge（unit:m）

3.2 计算结果

3.2.1 主缆坐标3种方法计算的成桥恒载状态下主缆坐标、空缆状态下主缆坐标，分别列于表1、表2中.

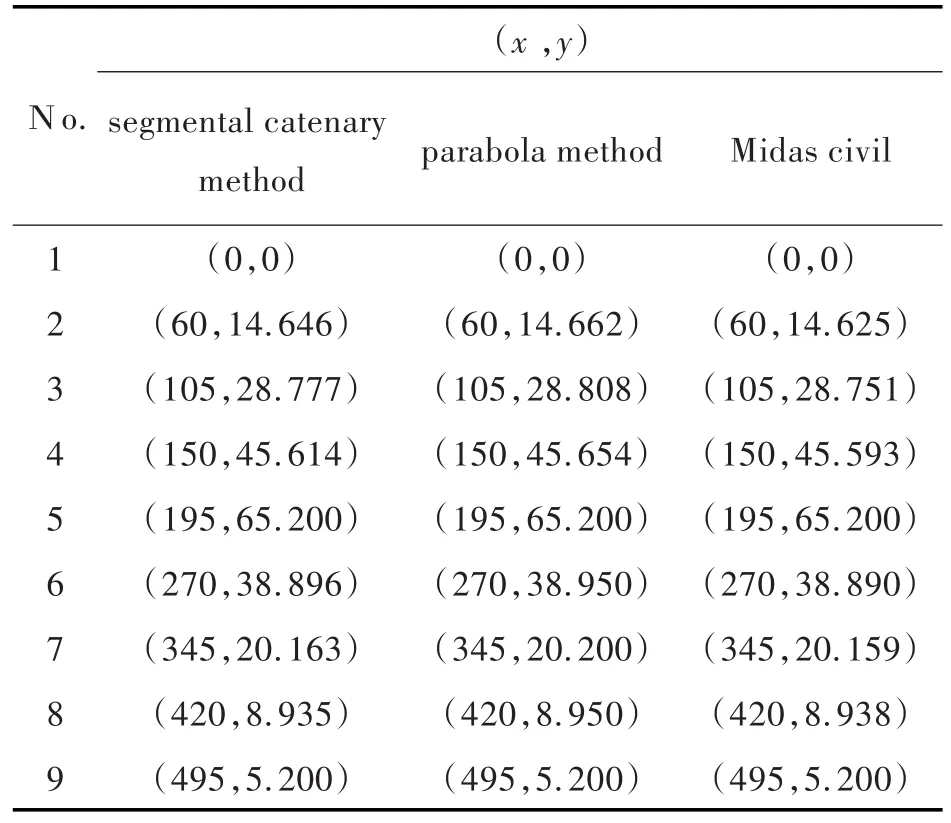
表1 成桥恒载状态下的主缆坐标（单位：米）Tab.1Coordinates of main cable under dead load state（unit：m）

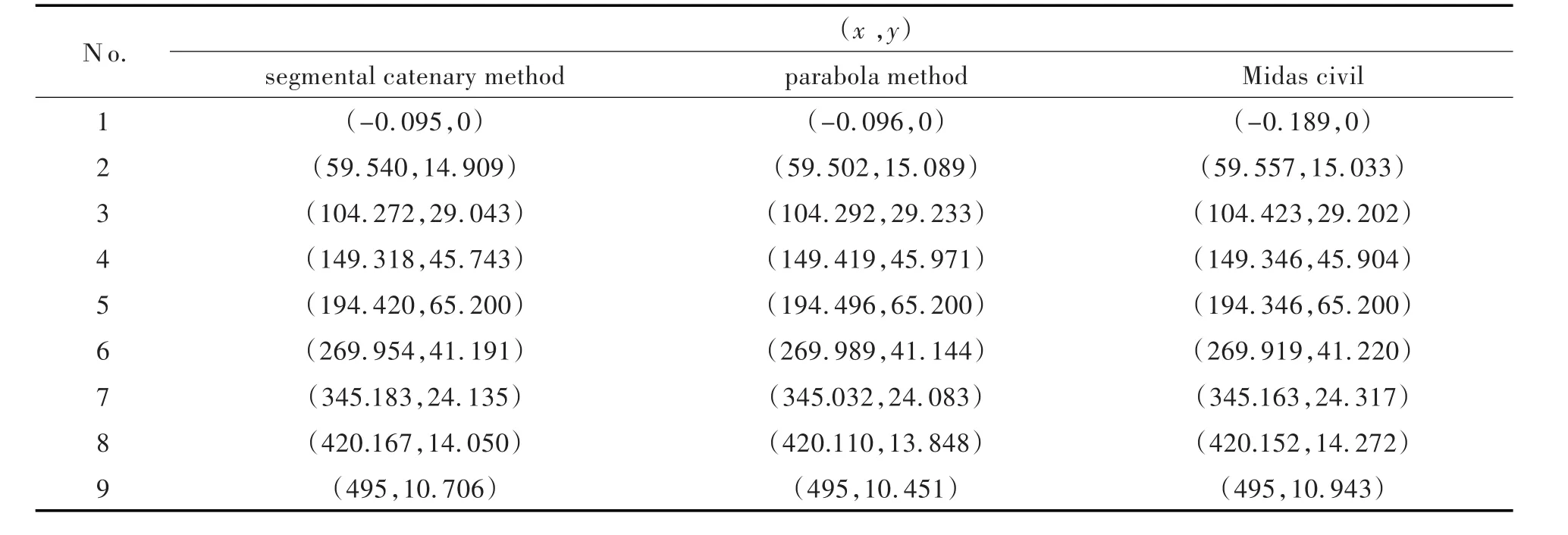
表2 空缆状态下的主缆坐标（单位：米）Tab.2Coordinates of main cable under empty load state（unit：m）

从表1和表2可以看出，成桥恒载作用下，3种方法计算的吊点坐标较为一致，最大相对误差为0.2%.空缆状态下，最大相对误差为0.14%.分段悬链线与有限单元法计算结果较为吻合.

3.2.2 索长和索鞍预偏量主缆索长和索鞍预偏量对桥梁的几何构形和初始受力状态具有较大影响，若存在较大误差，将会对施工阶段的索塔受力带来安全隐患，须加以重视并解决.索长列于表3、表4中，索鞍预偏量列于表4中.

表3 成桥恒载状态的索长Tab.3Cable under dead load state

表4 空缆状态的索鞍预偏量和索长Tab.4Pre-bias of cable saddle and cable length under empty load state

从表3和表4可以看出，成桥状态和空缆状态下，有应力索长和无应力索长，多段悬链线法与Midas civil计算结果误差较小；索鞍预偏量存在误差，多段悬链线法更接近有限单元法，抛物线法误差较大，误差为0.15 m，相对误差为23%.

4 结语

1）基于分段悬链线法自编程序计算结果与Midas Civil软件计算结果基本吻合，用于大跨度自锚式悬索桥成桥、空缆线形分析，能够达到设计和施工要求的精度.

2）对于成桥恒载状态，分段悬链线法和抛物线法均可满足工程设计和施工的精度要求，但空缆的吊点坐标和索鞍预偏量结果表明，抛物线法误差较大.

3）分段悬链线与抛物线法均没有考虑散索点的约束对线形的影响，且计算精度决定于对各吊杆力的计算与分配，因此仍存在一定的近似性，正确的处理方法应与有限元法计算结果对比分析，经反复修正迭代后，综合防治确定.

［1］WOLLMANN G P，OCHSENDORF J A，ILLINGTON D P.Self-anchored suspension bridges［J］.Journal of bridge engineering，2001，6（2）：156-158.

［2］张哲.混凝土自锚式悬索桥［M］.北京：人民交通出版社，2005.

［3］OCHSENDORF J A，BILLINGTON D P.Self-anchored suspension bridges［J］.Journal of bridge engineering，1999，4（3）：151-156.

［4］王桢.超大跨径自锚式悬索桥几何非线性行为理论与实验性能研究［D］.重庆：重庆交通大学，2013.

［5］邱文亮.自锚式悬索桥非线性分析与实验研究［D］.大连：大连理工大学，2003.

［6］刘钊，刘厚军.悬索桥主缆变形及重力刚度新算法［J］.工程力学，2009，26（6）：127-132.

LIU Z，LIU H J.New arithmetic for cable deflection and gravity stiffness of suspension bridges［J］.Engineering mechanics，2009，26（6）：127-132.

［7］肖海波.自锚式悬索桥的力学特性分析［D］.杭州：浙江大学，2004.

［8］张志国，张庆芳，邹振祝.悬索桥成桥状态计算方法［J］.长安大学学报（自然科学版），2006，26（1）：59-62，66.

ZHANG Z G，ZHANG Q F，ZOU Z Z.Analytical methods of suspension bride geometry under dead loads［J］.Journal of Chang'an university（natural science edition），2006，26（1）：59-62，66.

［9］王国兴.自锚式悬索桥主缆线形控制与吊索张拉分析［D］.西安：长安大学，2008.

［10］张炎.自锚式悬索桥主缆线形及吊索张拉方案研究［D］.重庆：重庆交通大学，2014.

［11］杨勇.非对称悬索桥主缆线形程序开发与参数分析［D］.重庆：重庆交通大学，2010.

［12］张佳文，赵彬.悬索桥主缆成桥线形的解析迭代计算方法［J］.湘潭大学自然科学学报，2011，33（1）：47-52.

ZHANGJW，ZHAOB.Calculationmethodof iterative analysis on main cable shape of suspension bridges［J］.Natural science journal of Xiangtan university，2011，33（1）：47-52.

［13］KIM H K，LEE M J，CHANG S P.Non-linear shapefinding analysis of a self-anchored suspension bridge［J］.Engineering structures，2002，24（12）：1547-1559.

［14］肖汝诚，项海帆.大跨径悬索桥结构分析理论及其专用程序系统的研究［J］.中国公路学报，1998，11（4）：42-50.

XIAO R C，XIANG H F.Research on the structural analysis theoryandspecial programof long-span suspension［J］.China journal of highway transport，1998，11（4）：42-50.

［15］邱顺冬.桥梁工程软件midas_civil应用工程实例［M］.北京：人民交通出版社，2011.

本文编辑：苗变

Computation and Error Analysis of Main Cable Configuration of Large-Span Self-Anchored Suspension Bridges

YANG Heng，LI Yuansong*，QI Chao，ZHOU Xiaolong
School of Resource and Civil Engineering，Wuhan Institute of Technology，Wuhan 430074，China

Aimed at the change characteristics of the main cable configuration of self-anchored suspension bridge in construction process，we developed the program of segmental catenary method and parabola method to realize the accuracy computation of geometrical parameters of large-span self-anchored suspension bridges，such as main cable configuration，unloaded cable configuration，stress-free length of individual segments，hoist point coordinates，and pre-bias of cable saddle，etc.The results of the self-developed program and Midas civil software were compared with a project.The relative error of pre-bias of cable saddle is 11.3%by the segmental catenary method and is 23%by the parable method compared with that by the finite element method.We suggest that the results of segmental catenary method and parabola method should be modified and iterated repeatedly to determine the main configuration synthetically in construction process.

self-anchored suspension bridge；main cable configuration；segmental catenary method；parabola method

U448.25

A

10.3969/j.issn.1674-2869.2016.06.010

1674-2869（2016）06-0565-06

2016-05-12

武汉工程大学研究生创新基金（CX2015040）

杨恒，硕士研究生.E-mail：358031860@qq.com

*通讯作者：李元松，博士，教授.E-mail：li_yuan_song.@126.com