轻型组合桥面板中小栓钉连接件的静力及疲劳性能
张士红,邵旭东,黄细军,3,杨 波
(1.湖南大学 桥梁工程研究所,湖南 长沙 410082;2.河南省交通规划设计研究院股份有限公司,河南 郑州 450052;3.中铁大桥勘测设计院集团有限公司,湖北 武汉 430056)
轻型组合桥面板中小栓钉连接件的静力及疲劳性能
张士红1,2,邵旭东1,黄细军1,3,杨 波1
(1.湖南大学 桥梁工程研究所,湖南 长沙 410082;2.河南省交通规划设计研究院股份有限公司,河南 郑州 450052;3.中铁大桥勘测设计院集团有限公司,湖北 武汉 430056)
为探究轻型组合桥面板UHPC薄层中小尺寸栓钉连接件的静力和疲劳性能,对总计6个试件进行了静力加载和疲劳试验。基于显式动态分析方法,采用ABAQUS软件进行了静力推出试验的数值分析;随后又设计9个正交试验开展了栓钉参数分析及特征值影响因素显著性分析。最后,基于一个实际工程,对轻型组合桥面板中小栓钉连接件的疲劳强度进行验算。结果表明:(1)UHPC薄层中的小栓钉仍具有较好的承载力,其承载力设计值可偏安全地按照Eurocode-4规范的计算式取值,即Pd=0.8Asfu/γv。(2)UHPC薄层中的小栓钉承载力主要受栓钉的直径和屈服强度影响,滑移特征值主要受栓钉的高度影响,抗剪刚度主要受栓钉的直径影响。(3)疲劳试件破坏前的很长一段时间内,滑移量增长缓慢且增量较小,在试件疲劳破坏阶段,滑移值增速较快且增量明显。基于断裂力学方法的栓钉疲劳寿命估算值与实测值基本吻合。(4)小栓钉连接件的疲劳强度满足洞庭湖二桥轻型组合桥面板的设计要求。
桥梁工程;轻型组合桥面板;静力和疲劳试验;小栓钉;显式动态分析;断裂力学
0 引言
UHPC(抗压强度>150 MPa,抗拉强度>7 MPa)材料的出现,结构有望突破原有尺寸上的限制,趋于更加纤细、轻薄。为解决传统正交异性钢桥面板的钢结构疲劳和铺装层易损等难题,文献[1]提出了将具有高弹性模量、高抗拉强度的密配筋UHPC层加铺在钢桥面板上,形成新型“轻型组合桥面板”结构。研究表明[2],钢桥面板与UHPFRC(也称“UHPC”,这里按原文表述)层之间的相对滑移会导致UHPFRC层底面和钢结构的应力增大,工程中需采取措施保证两者之间的有效黏结。轻型组合桥面板中,通常采用栓钉连接件来实现钢桥面板与UHPC层之间协同工作[1],栓钉是保证轻型组合桥面板结构发挥有效作用的关键构件。
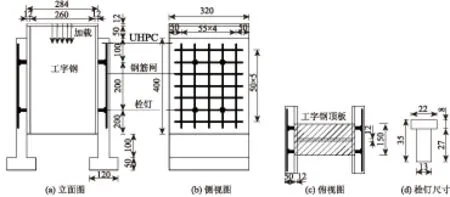
图1 试件几何尺寸(单位:mm)Fig.1 Geometric dimensions of specimen (unit: mm)
轻型组合桥面板结构中,UHPC层厚度通常为35~50 mm,为满足一定的保护层厚度要求,同时方便栓钉施焊,栓钉的高度宜满足40 mm≥h≥25 mm。AASHTO规范[3]和Eurocode-4规范[4]分别要求组合结构中栓钉的高度(h)与直径(d)比大于4和3;另外,AASHTO规范要求栓钉的保护层厚度大于50 mm,而Eurocode-4规范则要求栓钉保护层厚度大于20 mm,且栓钉的钉帽以下部分伸入混凝土的长度大于30 mm。埋置于UHPC薄层中的小栓钉,其静力和疲劳性能与普通混凝土组合结构中常用的大尺寸栓钉(h≥65 mm,d≥19 mm)定会有所不同,且其h/d和保护层厚度均不满足规范要求,需开展相关试验及理论研究,以探明轻型组合桥面板中小栓钉连接件的静力及疲劳性能。
文献[5]基于ANSYS有限元软件对5个不同参数的静力推出试验进行了分析,同时进行了1个静力加载试验,探究了RPC中小栓钉(h/d=1.7~2.7)的静力特性。结果表明,试件的破坏形态均为栓钉破坏,栓钉直径d是决定试件抗剪承载力的关键因素,并提出了RPC中小栓钉的承载力计算公式;文献[6]进行了5组静力推出试验,研究了UHPC中栓钉(100≥h≥50 mm,22 mm≥d≥16 mm)的承载力和抗剪刚度特性,并与规范中的栓钉承载力计算值对比,结果表明,AASHTO规范中的栓钉承载力公式与试验值吻合最好。至于UHPC中小栓钉疲劳性能的研究,更鲜见于文献。本文设计6个推出试件,进行了静力和疲劳试验,并采用ABAQUS软件进行了栓钉的参数分析,以探究UHPC薄层中小栓钉的静力和疲劳性能。
1 试件模型
参考Eurocode-4规范[7],同时兼顾轻型组合桥面板的结构特点,设计6个推出试件,主要尺寸见图1。其中,UHPC板厚50 mm,板内配置间距为50 mm×55 mm(纵向×横向)的φ10的冷拔带肋钢筋。推出试件采用材质为Q345 的I型钢,两侧各焊4个栓钉。栓钉采用GB/T 10433—2002《电弧螺柱焊用圆柱头焊钉》[8]规定的材质为ML15A的栓钉,直径13 mm,高35 mm,布置间距为200 mm×110 mm(纵向×横向)。推出试件中各材料的力学性能如表1所示。
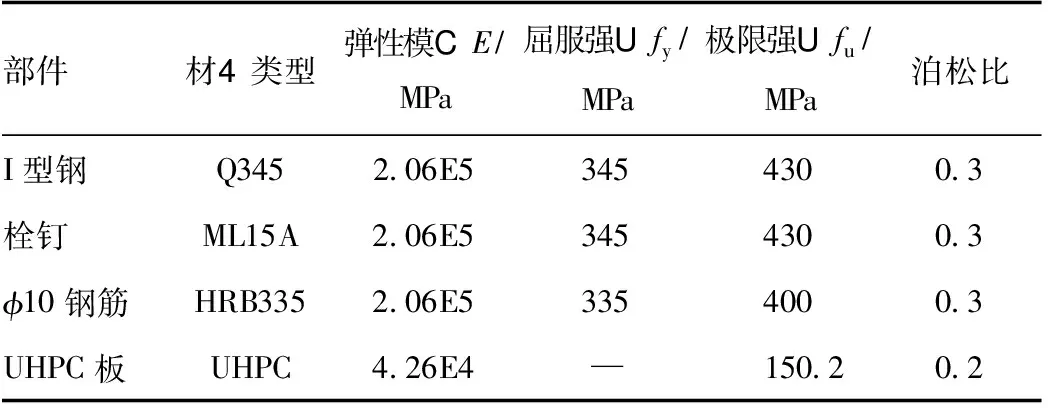
表1 主要材料的力学性能Tab.1 Mechanical property of main materials
注:I型钢和栓钉的材料性能由供应商提供;UHPC的极限强度指28天立方立体抗压强度值。
6个试件分别记为S-1~S-3和F-1~F-3。其中,试件S-1在I型钢、栓钉和UHPC板之间的界面上涂抹润滑油,以消除界面之间的黏结作用。其他5个试件的界面之间均保留自然黏结,未做特殊处理。其中,试件S-1~S-3进行静力加载试验,试件F-1~F-3进行疲劳试验。
2 静力试验
2.1 试验装置
试件S-1~S-3进行静力加载试验。试件基座与地面之间加一层橡胶垫并撒一层细的石英砂,同时在试件顶部设置球铰,并严格对中试件以避免产生偏心。试验正式开始前进行3次预加载试验,以检测仪器是否正常工作;正式加载采用单调分级加载,以25 kN为一级,每级持荷3~5 min,待仪表读数稳定后进行试验数据的采集。在试件的底基座位置固定千分表,以记录UHPC板与I型钢之间的相对滑移;试验过程中还记录了荷载值和UHPC板表面的应变值。静力试验装置如图2所示。
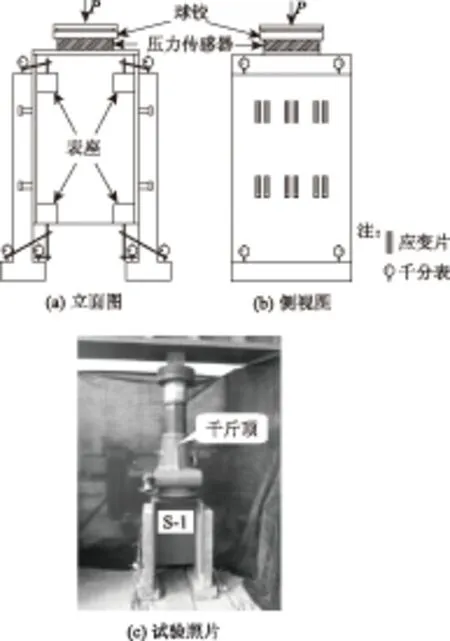
图2 静力试验装置Fig.2 Equipment of static test
2.2 试验结果
试验加载初期,试件未发生显著的变化,UHPC板与I型钢之间的相对滑移较小;当加载至80%~90%峰值荷载时,部分栓钉屈服,UHPC板与I型钢之间的相对滑移开始显著增大;当荷载达到峰值时,部分栓钉被剪断,此时已无法记录试件的荷载-滑移曲线,试验结束。整个试验过程中,UHPC板未出现劈裂现象,表面也未出现任何可见裂缝。3个试件的最终破坏形态都是栓钉的剪断,破坏形态如图3所示。

图3 静力试验试件破坏形态Fig.3 Failure modes of specimens in static test
试件S-1 ~S-3的静力试验主要结果如表2所示。
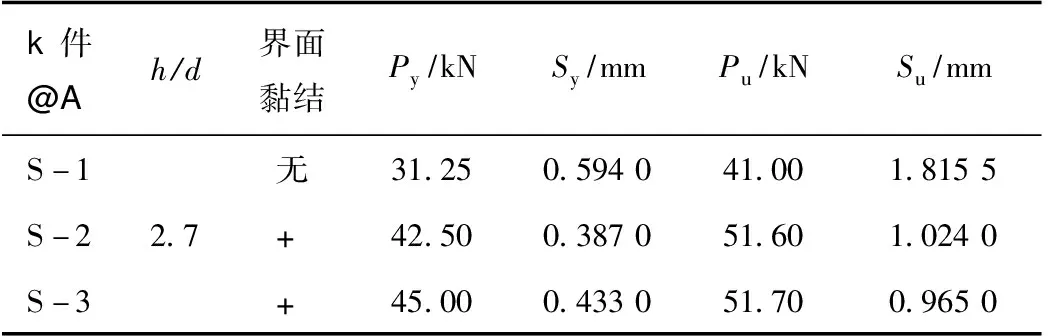
表2 静力试验结果Tab.2 Result of static test
注:Py为单个栓钉屈服时的平均荷载值;Pu为单个栓钉的平均最大承载力值;Sy为荷载Py对应的滑移值;Su为荷载Pu对应的滑移值。
静力试验结果表明:试件的破坏源于栓钉根部被剪断,这与文献[5-6]的结果一致;尽管栓钉保护层厚度不满足现有规范要求,但在静力试验过程中,UHPC板均未出现劈裂,表面也未出现任何裸眼可见的裂缝;试件S-1的承载力比S-2~S-3低20.6%左右,且滑移值较大,可见UHPC板与I型钢之间的黏结作用对试件抗剪承载力有一定的影响。
单个栓钉平均抗剪承载力试验值与各国规范建议的计算值比较见表3。
表3 单个栓钉承载力试验值与规范计算值对比(单位:kN)
Tab.3 Comparison of shear capacity of single stud between test value and calculation value based on specification(unit:kN)
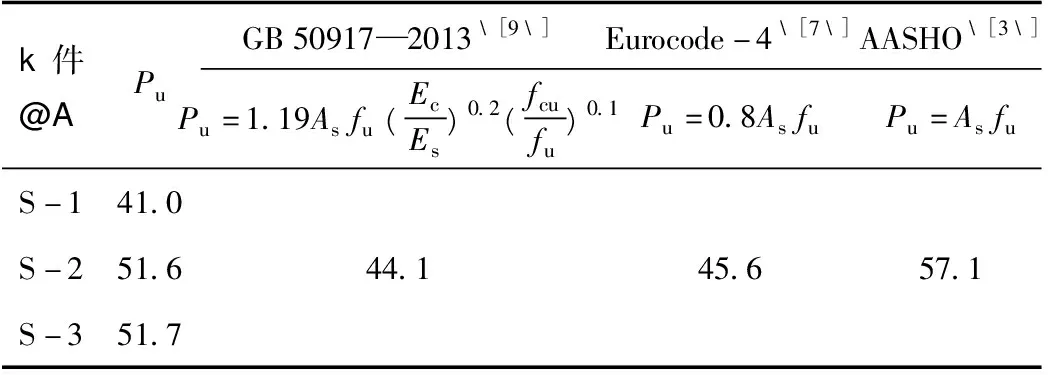
试件编号PuGB50917—2013[9]Eurocode-4[7]AASHO[3]Pu=1.19Asfu(EcEs)0.2(fcufu)0.1Pu=0.8AsfuPu=AsfuS-141.0S-251.6S-351.744.145.657.1
注:As为栓钉横截面面积;σmax,Vs为混凝土和栓钉的弹性模量;Vs=min(Asfd,Acfc)为混凝土的立方体抗压强度标准值;fu为栓钉极限抗拉强度。
由表3可知,如果按照实际工程中UHPC板与钢面板保持界面自然黏结的状态,对于UHPC薄层中的小栓钉来说:采用GB 50917—2013和Eurocode-4规范得到的栓钉承载力计算值接近,且都比试验值小,偏保守;而采用AASHTO规范的计算值高于试验值,偏不保守。因此,UHPC薄层中小栓钉的承载力设计值Pd可偏安全地按照Eurocode-4规范的计算式Pd=0.8Asfu/γv得到,其中,γv为安全系数,推荐值为1.25。
2.3 有限元分析
2.3.1 材料本构关系
采用ABAQUS有限元软件进行推出试验的建模分析。其中,UHPC轴拉、轴压本构关系参考文献[10];钢筋本构关系采用理想的弹塑性模型。有限元建模时,把I型钢和栓钉作为一个部件,共同建模,并赋予相同的材料属性。由于在试验中,一般栓钉先发生破坏而I型钢不会破坏,因而这里I型钢和栓钉采用相同的本构关系,即三折线模型,可参考文献[11]。
为得到精确完整的荷载-滑移曲线,有限元分析中,所有材料的本构关系都包含了材料的损伤初始准则。UHPC材料的损伤模拟采用ABAQUS软件材料库中的混凝土塑性损伤模型;栓钉采用延性和剪切准则来模拟金属的断裂失效,相关参数一般由试验确定,本文参考文献[12]取值。材料一旦达到相应的破坏准则,刚度就会按照软化法则降低,直至完全失效,此时,单元就会从有限元模型中移除。
2.3.2 单元类型与网格划分
有限元模型包括UHPC板、栓钉、I型钢、加载板和钢筋网5个部分。其中,UHPC板、栓钉和I型钢均采用三维实体线性缩减积分单元(C3D8R)模拟,并将栓钉和I型钢建立在同一部件中以模拟二者之间的连接。钢筋采用三维实体管单元(T3D2)模拟。考虑到试件具有对称性,为节省计算费用,建立1/4推出试件的有限元模型进行分析。采用扫略网格技术对有限元模型网格进行划分,其中,UHPC板与栓钉交界面处和栓钉与I型钢的连接处等应力集中区采用较细的网格,单元网格尺寸2 mm左右,其他部分采用较粗的网格,单元网格尺寸10 mm左右。推出试件的有限元网格划分如图4所示。
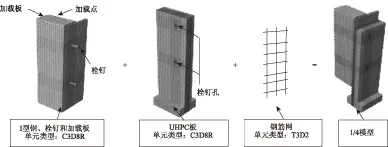
图4 单元类型及网格划分Fig.4 Element types and meshing
2.3.3 接触模拟
为简单起见,本文有限元分析均不考虑UHPC板与I型钢之间的黏结作用。当不考虑界面之间的摩擦时,I型钢与UHPC板之间、栓钉与UHPC间的接触面接触仅采用硬接触,接触面之间能够传递的接触压力大小不受限制,而当接触面的压力变为负值或者零就表示两个接触面发生分离[13];当考虑界面之间的摩擦时,摩擦系数取0.25[12],I型钢与UHPC板之间、栓钉与UHPC界面的接触由法线方向的硬接触和切线方向的罚函数两部分组成。钢筋单元采用ABAQUS中的嵌入(Embedded region)约束,软件可自动耦合钢筋和周围UHPC的自由度,并忽略二者之间的黏结滑移效应。
2.3.4 边界与加载
在1/4推出模型的两个对称面上分别施加相应的对称边界条件;在模型下部支座位置约束所有节点的全部自由度。有限元分析中,荷载通过位移加载方式模拟,大小按平滑的幅值函数规律增加。
2.3.5 分析方法
显式非线性动态分析方法广泛运用于混凝土的裂缝和失效模拟、金属成型、冲击等分析中,在求解非连续和接触问题中十分有效,同时也可用于准静态(quasi-static)分析[12]。因此,本文采用显式非线性动态分析方法,对推出试验进行有限元模拟。理论上,可按照静力推出试验的实际加载速率对推出试验进行有限元模拟。本文采用不同的速率进行试加载,考虑计算精度和求解费用,最终确定有限元分析中荷载的加载速率为0.1 mm/s。
2.3.6 模型验证
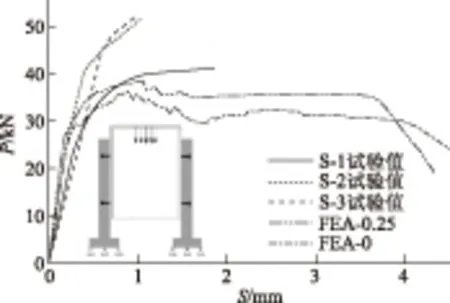
图5 单个栓钉的平均荷载-滑移曲线Fig.5 Average load-slip curves of single stud
采用ABAQUS有限元软件对试件S-1~S-3的静力推出试验进行数值模拟,得到单个栓钉平均荷载-滑移曲线与试验值对比如图5所示。其中,“FEA-0.25”指有限元计算时考虑界面之间的摩擦,摩擦系数取0.25;“FEA-0”指有限元计算时不考虑界面之间的摩擦。
由于试验中荷载的加载速率较难控制,静力加载试验并没有得到荷载-滑移曲线的下降段,而采用显式非线性动态分析方法可以较完整地模拟出试件破坏的全过程。由图5可知:栓钉的承载力有限元计算值比试验值低,与试件S-1的试验值最接近;考虑界面之间的摩擦(FEA-0.25)比不考虑界面之间的摩擦(FEA-0)的栓钉连接件承载力Pu大6%,界面之间的摩擦对栓钉连接件承载力Pu没有显著影响,但对栓钉的抗剪刚度ksc有一定的影响,考虑界面之间的摩擦比不考虑摩擦时ksc大13.1%。有限元计算表明,试件破坏时的滑移值特征值在3.34~3.70 mm左右,小于Eurocode-4规范规定的栓钉延性应大于6 mm的要求。
2.4 栓钉参数分析
为探究UHPC薄层中栓钉参数对试件的静力特性的影响,考虑栓钉的直径(d)、高度(h)及屈服强度(fy)3个主要因素,按照正交试验方法,选用L9(34)正交表,设计9个静力推出试验,记为SA-1~SA-9,进行有限元分析。9个静力推出试件的几何尺寸及加载方式参考图1,栓钉的因素水平如表4所示。试件SA-1~SA-9的有限元建模和分析方法同2.3节,且不考虑界面之间的摩擦,主要计算结果如表5所示。
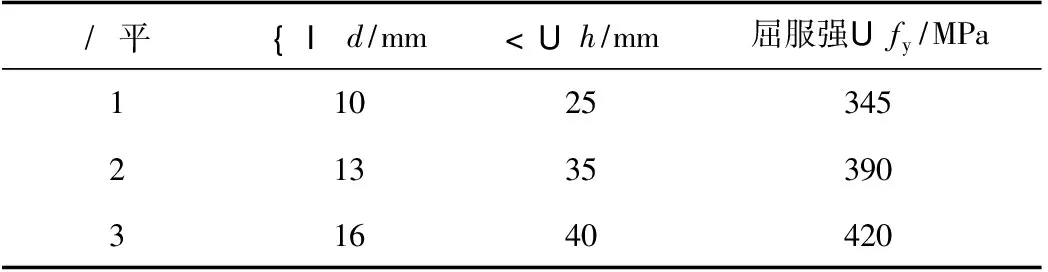
表4 栓钉的因素水平表Tab.4 Factor levels for stud
依据Eurocode-4规范[7]规定,栓钉的抗剪刚度为
ksc=0.7PRk/s(kN/mm),
(1)
式中,PRk为标准推出试验得到的栓钉抗剪承载力特征值,有PRk=0.9Pu;s为0.7PRk荷载值对应的滑移量。同时,将栓钉抗剪承载力特征值PRk对应的滑移值定义为滑移特征值δu。
由表5、表6的参数分析表明:栓钉的承载力Pu主要受栓钉的直径d和屈服强度fy影响。其中,栓钉直径d影响高度显著,栓钉屈服强度fy影响显著;试件的滑移特征值δu主要受栓钉高度h影响,但影响不显著;抗剪刚度ksc主要受栓钉的直径d和高度h的影响,其中,栓钉直径d影响高度显著。
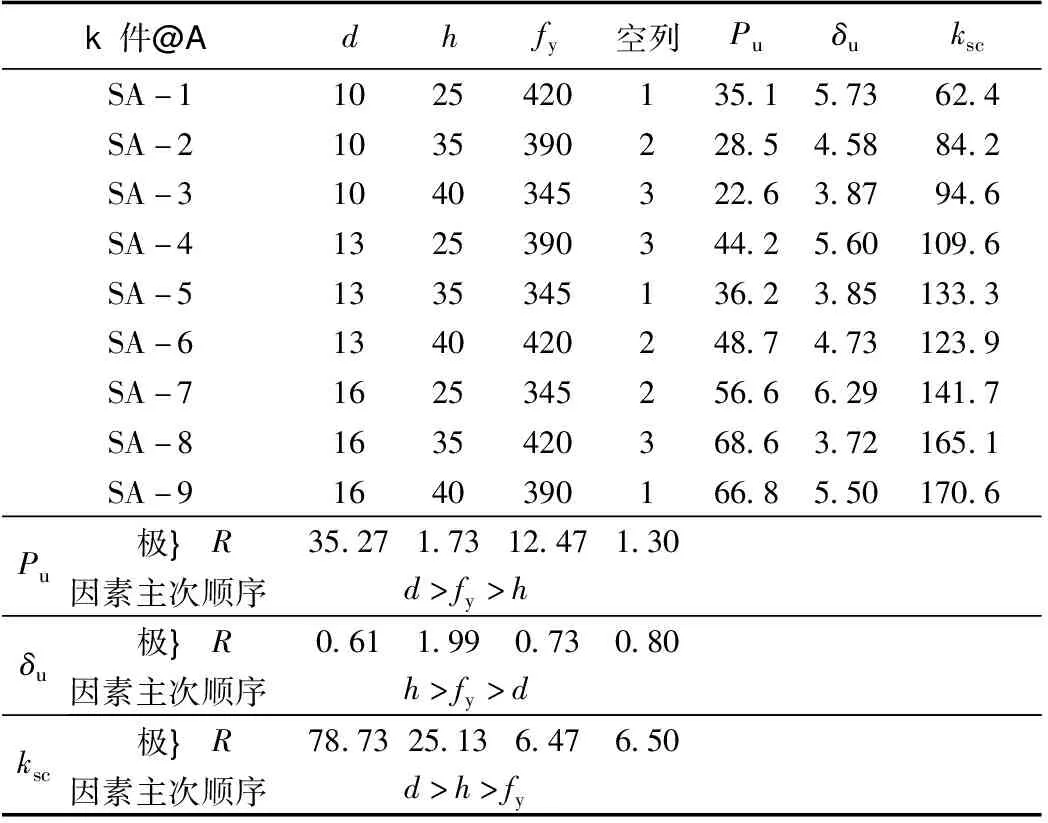
表5 正交试验有限元计算结果(h/d=1.6~4)Tab.5 FE calculation result for orthogonal test (h/d=1.6~4)
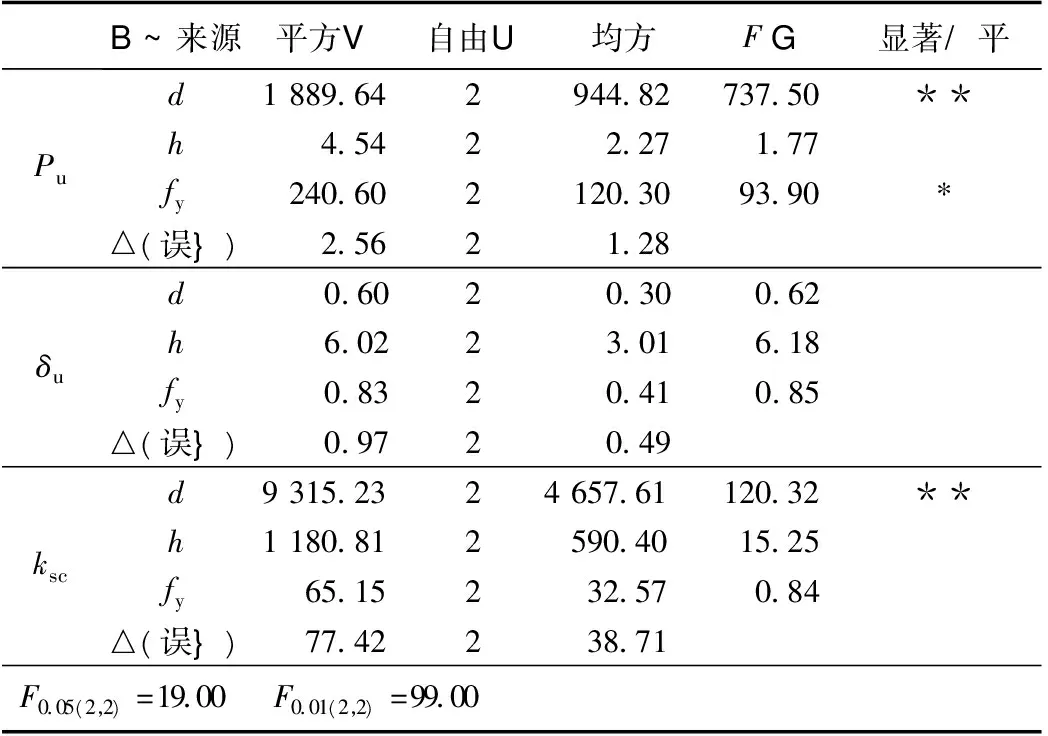
表6 显著性检验Tab.6 Significant test
3 疲劳试验
栓钉连接件的受力不仅要满足静力承载力要求,还需要满足疲劳要求。我国钢-混凝土组合桥梁设计规范[9]规定,栓钉连接件的最大剪力幅不超过其抗剪承载力的0.2倍。本文设计了栓钉连接件的剪力幅在0.29~0.37范围变化的3个试件F-1~F-3进行疲劳加载试验。采用PMS-500型数显式脉动疲劳试验机对试件进行常幅正弦荷载加载,加载频率为5.0 Hz。在试件的I型钢的腹板上,固定WA100动位移传感器(测量精度为0.001 mm),可随时记录I型钢与UHPC板之间的相对滑移值。在疲劳动载循环进行到0,1,5,10,20,50,100,150,200万次时,分别停机进行静力加载试验,得到不同动载循环次数后的荷载-滑移曲线。疲劳试验装置如图6所示。

图6 疲劳试验装置Fig.6 Equipment of fatigue test
3.1 试验结果
试件F-1~F-3分别在疲劳循环加载进行到240.5,168.8万次和60.0万次时,栓钉被剪断,试件破坏,试验停止。F-1~F-3试件在疲劳试验加载初期,I型钢与UHPC板之间贴合紧密,无分离趋势,随着加载次数的增加,I型钢翼板与UHPC板之间的最大滑移值缓慢增加,随后I型钢翼板与UHPC板出现分离间隙,直至二者完全分离。在试件疲劳寿命的末期,I型钢翼板与UHPC板之间的最大滑移值不断增加,最终一侧的栓钉被剪断,I型钢与UHPC板分离,疲劳试验结束。试验结束后,检查试件,发现栓钉均从根部被剪断,而UHPC板基本完好无损,仅栓钉根部位置有少量粉末状颗粒。试件破坏形态如图7所示。

图7 疲劳试验试件破坏形态Fig.7 Failure modes of specimens in fatigue test
试件F-1~F-3的疲劳试验主要结果如表7所示。

表7 疲劳试验结果Tab.7 Result of fatigue test
3.2 基于断裂力学的栓钉疲劳寿命估算
这里以单个栓钉为例。对于组合结构中的栓钉连接件来说,其主要承受剪应力,栓钉的疲劳裂纹通常源于栓钉的焊趾处,并沿栓杆截面不断扩展,当栓钉难以承担界面之间的剪力时栓钉发生疲劳破坏。其中,裂纹的扩展速率da/dN是应力强度因子幅值ΔK的函数,满足Paris公式:
,
(2)
式中,C,m为材料常数,可由试验数据拟合得到;a为裂纹长度;N为疲劳循环次数。
基于Paris公式可推导得到栓钉的疲劳寿命N,见式(3),详细推导过程可参考文献[16],限于篇幅这里不再赘述:
,
(3)
式中,Δτ为栓钉的剪应力幅;a0为初始裂纹特征长度,可假定a0=2 mm[14];ac为疲劳破坏时的裂纹特征长度,满足式(4)[15]:
。
(4)
式(3)~(4)表明,栓钉的疲劳寿命不仅与栓钉的剪应力幅Δτ有关,而且还与疲劳荷载上峰值Pmax、栓钉直径d、初始缺陷a0以及栓钉的承载力值Pu等因素有关。
对于试件F-1~F-3,根据静力和疲劳试验结果,联立式(3)、(4)可得栓钉的疲劳寿命估算值Nc,与栓钉疲劳寿命实测值Nt的对比如表8所示。
用人本身就是一项艺术,人无完人但是各有其长。作为学校来说,也是有岗位差异的,不同的岗位对于教师的要求是不同的,一线教师需要教育教学能力强的教师;而教辅部门则需要工作细致的教师。各处室则需要服务意识强,工作有耐心的教师。所以需要树立正确的用人观。
综合表7、表8可知:UHPC薄层中小栓钉的疲劳机理与普通混凝土中的相似,试件的疲劳破坏源于栓钉根部的疲劳断裂,而UHPC板完好无损;疲劳试验初期,I型钢翼板与UHPC板之间的最大滑移值增加缓慢,而在疲劳试验末期,二者之间的最大滑移值不断快速增加,最终一侧栓钉被剪断;栓钉疲劳寿命的估算值与实测值吻合较好,基于断裂力学方法可以较好地预测UHPC中小栓钉的疲劳寿命。
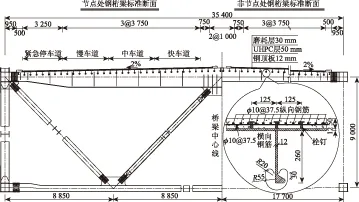
图8 钢桁梁标准横断面图(单位:mm)Fig.8 Standard cross-section of steel truss girder (unit: mm)
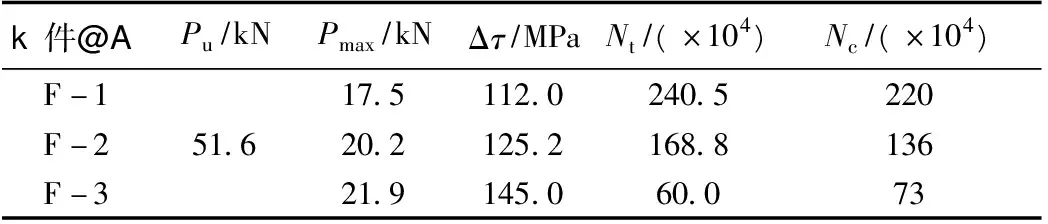
表8 栓钉的寿命试验值与估算值对比Tab.8 Comparison of life of stud between test value and calculation value based on specification
4 轻型组合桥面板中小栓钉的疲劳验算
以在建的洞庭湖二桥轻型组合桥面板为工程背景。洞庭湖二桥为双塔双跨钢桁梁悬索桥,垂跨比1/10,主跨1 480 m,全长2 390 m。初步设计方案中,加劲梁桁高9.0 m,桥面全宽35.4 m,钢桁梁顶板厚12 mm,横梁高1.38 m,横肋高0.75 m,每隔2.8 m设一道横梁或横肋,横隔板厚10 mm。纵肋采用HP260×12(高度×厚度,单位:mm)的球扁钢,间距500 mm。钢顶板上焊上长35 mm,直径13 mm的栓钉,间距125 mm×125 mm(纵向×横向)。然后再绑扎φ10的HRB335钢筋,其纵、横向间距均为37.5 cm,形成钢筋网。最后浇注50 mm厚的UHPC层,采用蒸汽养护,形成轻型组合桥面板结构,如图8所示。
对于轻型组合桥面板来说,栓钉属于局部构件,其受力状态与轻型组合桥面板的局部构造密切相关。采用ANSYS有限元软件建立洞庭湖二桥的局部有限元模型,见图9,纵桥向包括6跨横隔板间距长度,考虑到结构的对称性,横向采用半幅结构。需要说明的是,为建模方便,局部有限元模型中,按照剖面面积和惯性矩等效原则,将球扁钢纵肋等效为“L”型纵肋。
局部有限元模型中,钢板(弹性模量为2.1×105MPa,泊松比为0.3)采用SHELL91模拟;UHPC(弹性模量为4.26×104MPa,泊松比为0.2)采用SOLID95单元模拟;栓钉采用COMBINE14单元模拟,以考虑纵、横桥向的抗剪作用,抗剪刚度取ksc=133.3 kN/mm(表5)。有限元计算中,忽略UHPC层与钢板之间的黏结作用,在栓钉以外的其他位置仅为耦合钢板与UHPC的竖向位移。
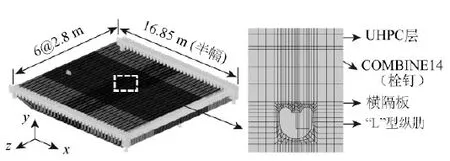
图9 局部有限元模型Fig.9 Local finite element model
局部有限元模型的边界条件为:在端横隔板截面处,约束端部的纵向(Z向)平动自由度和绕竖向(Y向)与横轴(X向)的转动自由度;在道路中心线截面处,采用横向(X向)对称约束;在有吊索位置的横隔板底板位置处,约束其竖向(Y向)平动自由度;在桁架节点处,约束钢桁梁横隔板底板的全部自由度。
疲劳荷载采用Eurocode 1[16]中的标准疲劳车型3,每轴轴重120 kN。由于栓钉的影响面有效范围很小(3~4个栓钉间距),且标准疲劳车型3的前、后轴轴距较大(相距6 m),因此,可忽略前后车轴之间的叠加效应,同时忽略多车道效应而只采用标准疲劳车的后轴(120+120)kN进行加载。
选定部分典型位置的栓钉,采用机动法求得栓钉剪力的影响面后,采用标准疲劳车型3进行单迹线加载,可以看到栓钉的受力呈现以下特点:栓钉剪力影响面的有效范围较小,仅车轮作用区域的栓钉受到较大的剪力,远离车轮区域的栓钉受力较小;栓钉受力在空间上与具体的车道位置无关,不同车道位置的栓钉受力具有相似性;纵向剪力最大的栓钉位于横隔板上方位置(称之为“支承位置”),横向剪力最大的栓钉位于两个横隔板之间(称之为“跨中位置”)。
选取支承位置和跨中位置区域内的典型栓钉,计算得到栓钉的纵、横桥向剪应力幅。栓钉在承受纵、横向两个方向的剪力时,其等效剪应力幅为:
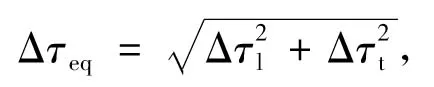
(5)
式中,Δτl和Δτt分别为栓钉纵、横桥向的剪应力幅;Δτeq为栓钉的等效剪应力幅。
依据Eurocode 1规范,采用标准疲劳车进行单车道加载得到的剪应力幅需要进行修正后才能反映影响线长度、重车数量、交通量以及其他车道重车的影响。栓钉的设计剪应力幅为:
Δτd=γMf×γFf×λ×Δτeq,
(6)
式中,γMf为结构重要性系数,这里取1.0;γFf为疲劳荷载效应分项系数,取1.0;λ为损伤等效系数,λ=λ1×λ2×λ3×λ4≤λmax。其中,λ1~λ4分别为跨径影响系数、荷载修正系数、交通量影响系数和其他车道重车影响系数。依据Eurocode 1规范可保守地取λ=λmax=2.5 (跨中位置),1.8 (支承位置)。由此可得栓钉的剪应力幅计算结果如表9所示。

表9 栓钉剪应力幅(单位:MPa)Tab.9 Shear stress amplitudes for stud (unit: MPa)
由表9可知,洞庭湖二桥轻型组合桥面板的小栓钉最大设计剪应力幅为67.53 MPa。由3.1节的疲劳试验结果可知,栓钉的疲劳强度(200万次)远大于67.53 MPa,且既有研究表明[17],推出疲劳试验中的栓钉的疲劳寿命要小于梁式试验的结果,结果偏于保守。因此,洞庭湖二桥轻型组合桥面板的栓钉疲劳强度能满足工程要求。
5 结论
本文对UHPC薄层中小尺寸栓钉连接件的静力和疲劳性能进行研究,得到的主要结论如下:
(1)静力试验结果表明:UHPC薄层中的小栓钉(d=13 mm,h=35 mm)仍具有较好的抗剪承载力,试件的破坏模式均为栓钉剪断,UHPC薄层中小栓钉的承载力设计值可偏安全地按照Eurocode-4规范的计算式Pd=0.8Asfu/γv得到。其中,γv为安全系数,推荐值为1.25;UHPC薄层中栓钉的保护层厚度仅15 mm时,试件破坏时UHPC板未出现劈裂和表面开裂现象。
(2)栓钉的参数分析表明:UHPC薄层中小栓钉的承载力主要受栓钉的直径d和屈服强度fy影响。其中,栓钉的直径d影响高度显著,栓钉的屈服强度fy影响显著;滑移特征值δu主要受栓钉的高度h影响,但影响不显著;栓钉的刚度ksc主要受栓钉的直径d和高度h的影响,其中栓钉的直径d影响高度显著。
(3)疲劳试验表明:试件疲劳破坏时UHPC板保持完好而未开裂,试件的疲劳破坏源于栓钉根部栓杆的疲劳断裂;试件破坏前的很长一段时间内滑移量增加缓慢且增量较小,在试件疲劳破坏阶段,滑移值增速较快且增量明显;栓钉疲劳寿命估算值与实测值吻合较好,基于断裂力学方法可以较好地预测UHPC薄层中小栓钉的疲劳寿命。
(4)基于实际工程的分析表明,采用规格为13 mm×35 mm (直径×高度),布置间距为125 mm×125 mm (纵向×横向) 的小尺寸栓钉连接件,能满足洞庭湖二桥轻型组合桥面板的疲劳要求。
[1] SHAO Xu-dong, YI Du-tao, HUANG Zheng-yu, et al. Basic Performance of the Composite Deck System Composed of Orthotropic Steel Deck and Ultrathin RPC Layer [J].Journal of Bridge Engineering, 2011,18(5):417-428.
[2] DIENG L, MARCHAND P, GOMES F, et al. Use of UHPFRC Overlay to Reduce Stresses in Orthotropic Steel Decks [J]. Journal of Constructional Steel Research, 2013, 89(5):30-41.
[3] AASHTO LRFD SI-2007, AASHTO LRFD Bridge Design Specifications [S].
[4] CEN 1994-2 Eurocode-4: 2005, Design of Composite Steel and Concrete Structures. Part 2: General Rules and Rules for Bridges [S].
[5] 邵旭东,周环宇,曹君辉.钢-薄层RPC组合桥面结构栓钉的抗剪性能[J].公路交通科技, 2013, 30 (4): 34-39,64. SHAO Xu-dong, ZHOU Huan-yu,CAO Jun-hui. Shear Behavior of Studs of Composite Deck System Composed of Steel and Ultra-thin RPC Layer[J]. Journal of Highway and Transportation Research and Development, 2013, 30 (4):34-39,64.
[6] KIM J S, KWARK J, JOH C, et al. Headed Stud Shear Connector for Thin Ultrahigh-Performance Concrete Bridge Deck [J]. Journal of Constructional Steel Research, 2015, 108: 23-30.
[7] CEN 1994-4-4 Eurocode-4: 2004, Design of Composite Steel and Concrete Structures. Part 1.1: General Rules and Rules for Buildings [S].
[8] GB/T 10433—2002,电弧螺柱焊用圆柱头焊钉[S]. GB/T 10433—2002, Cheese Head Studs for Arc Stud Welding[S].
[9] GB 50917—2013, 钢-混凝土组合桥梁设计规范[S]. GB 50917—2013, Code for Design of Steel and Concrete Composite Bridges [S].
[10]ZHANG Shi-hang, SHAO Xu-dong, CAO Jun-hui, et al. Fatigue Performance of a Lightweight Composite Bridge Deck with Open Ribs[J]. Journal of Bridge Engineering,2016,21(7):1-18.
[11]丁发兴,倪鸣,龚永智,等. 栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J]. 建筑结构学报, 2014, 35 (9): 98-106. DING Fa-xing, NI Ming, GONG Yong-zhi, et al. Experimental Study on Slip Behavior and Calculation of Shear Bearing Capacity for Shear Stud Connectors [J]. Journal of Building Structures, 2014, 35 (9): 98-106.
[12]NGUYEN H T, KIM S E. Finite Element Modeling of Push-out Tests for Large Stud Shear Connectors [J]. Journal of Constructional Steel Research, 2009, 65(10):1909-1920.
[13]石亦平. ABAQUS有限元分析实例详解[M]. 北京:机械工业出版社, 2012. SHI Yi-ping. Example Explanation of Finite Element Analysis Based on ABAQUS [M]. Beijing: China Machine Press, 2012.
[14]郭建生,孙国正. 用断裂力学法估算焊接钢结构的疲劳寿命[J].起重运输机械, 1999 (10): 9-12. GUO Jian-sheng, SUN Guo-zheng. Fracture Mechanics Method for Estimating the Fatigue Life of Welded Steel Structure[J]. Hoisting and Conveying Machinery, 1999 (10): 9-12.
[15]王宇航, 聂建国. 基于断裂力学的组合梁栓钉疲劳性能[J].清华大学学报:自然科学版,2009 (9): 1467-1470. WANG Yu-hang, NIE Jian-guo. Fatigue Behavior of Studs in a Composite Beam Based on Fracture Mechanics[J]. Journal of Tsinghua University:Natural and Science Edition, 2009 (9): 1467-1470.
[16]BS EN 1991-2:2005, Eurocode 1: Action on structure, Part 2: Traffic Loads on Bridges [S].
[17]LEE P G, SHIM C S, CHANG S P. Static and Fatigue Behavior of Large Stud Shear Connectors for Steel-concrete Composite Bridges [J]. Journal of Constructional Steel Research, 2005, 61(9):1270-1285.
Static and Fatigue Behaviors of Small Stud Shear Connector for Lightweight Composite Bridge Deck
ZHANG Shi-hong1,2, SHAO Xu-dong1, HUANG Xi-jun1,3, YANG Bo1
(1.Institute of Bridge Engineering, Hunan University, Changsha Hunan 410082, China; 2. Henan Provincial Communications Planning, Survey and Design Institute Co., Ltd., Zhengzhou Henan 450052, China; 3.China Railway Major Bridg Reconnaissance & Design Institute Co., Ltd., Wuhan Hubei 430056, China)
Static and fatigue tests are conducted on 6 specimens to investigate the static and fatigue properties of small stud shear connectors embedded in thin UHPC layer for lightweight composite bridge deck. The dynamic explicit analysis method is employed to conduct numerical analysis of static tests by ABAQUS software. Then, the parameter analysis and the significance analysis of the factors influencing eigenvalue are carried out based on 9 orthogonal tests. Finally, the fatigue strength of small stud shear connectors for lightweight composite bridge deck is calculated and checked based on a practical project. The result shows that (1) for small stud shear connectors embedded in thin UHPC layer, the shear capacity is reliable, and its design shear capacity can be conservatively calculated according to Eurocode-4, namelyPd=0.8Asfu/γv; (2) the shear capacity is mainly influenced by the diameter and yield strength of stud shear connectors, the eigenvalue of slip is mainly influenced by the height of stud shear connectors, and the shear stiffness is mainly influenced by the diameter of stud shear connectors; (3) there are no significant change in slip for a long period of time before failure of the specimen, the growth rate of slip is fast and the increment is obvious. The estimated value of fatigue life based on fracture mechanics method is consistent with the result of fatigue test; and (4) the fatigue strength of small stud shear connectors satisfies the requirements of the lightweight composite deck of the Second Dongting Lake Bridge.
bridge engineering; lightweight composite bridge deck; static and fatigue tests; small stud; dynamic explicit analysis; fracture mechanics
2016-03-03
国家自然科学基金项目(51178177, 51378194);交通运输部重大科技专项项目(2011318494160)
张士红(1990-),男,河南信阳人,硕士.(18229973845@163.com)
10.3969/j.issn.1002-0268.2016.11.017
U443.32
A
1002-0268(2016)11-0111-09

