边坡地震动力响应的振动台模型试验
马小莉,闫坤伐,刘晓燕,彭永涛,徐冠军
(1.榆林学院,陕西 榆林 719000;2.长安大学 特殊地区公路工程教育部重点实验室,陕西 西安 710064)
边坡地震动力响应的振动台模型试验
马小莉1,闫坤伐2,刘晓燕2,彭永涛2,徐冠军2
(1.榆林学院,陕西 榆林 719000;2.长安大学 特殊地区公路工程教育部重点实验室,陕西 西安 710064)
为研究坡面位置、地震动参数对加速度动力响应的影响,通过振动台模型试验,分析不同坡型的边坡动力响应,揭示了坡面形态、高程及地震波类型、振动强度、地震频率对动力响应的影响。试验结果表明:边坡模态参数与高程无关,随白噪声逐级加载,模型体系的一阶自振频率逐渐降低,阻尼比逐渐增加;凹坡测点加速度放大系数略大于凸坡相应测点,凹坡较凸坡不稳定;地震荷载下“高程放大效应”受边坡地形条件及地震动参数的影响呈现不同特征,凹坡高程放大效应较凸坡显著;坡内、坡表各测点的加速度放大系数呈折线递增趋势,但坡表各测点的加速度放大系数始终大于坡内;坡体动力放大效应与边坡自振频率密切相关,一定范围内,频率越高,放大效应就越显著;振动强度对边坡沿高程方向动力响应分布影响不大,但对边坡加速度放大效应的影响较为明显。
道路工程; 加速度放大系数; 振动台模型试验; 边坡动力响应; 地震;
0 引言
地震荷载作用下边坡的动力响应包括加速度、速度、位移以及应力应变等量值的响应[1-4],可用来判断边坡的稳定性,为预测边坡变形破坏提供重要手段,因而备受关注。
徐光兴[5-6]借助FLAC3D数值模拟与振动台试验对比得出:坡体表面PGA放大系数随输入地震波振动强度的增大而减小,随频率的增加也呈减小趋势;坡体内部位移随振动强度的增大而增大,随频率的增大而减小,持时表现出和振幅相同的特点。该模拟没考虑边坡形态、坡体材料等的影响。徐光兴[7-8]设计了凸坡、凹坡、斜坡土质边坡模型进行振动台对比试验,通过调整幅值对PGA放大系数进行研究得出了规律性的结论。影响边坡动力响应的因素很多仅考虑了坡型、地震动参数。许强[9-10]对水平层状上硬下软及上软下硬两种岩性组合模型进行振动台对比试验得出:加速度在竖直方向和水平方向的响应都表现出非线性特点,高程放大效应显著。冯志仁[11]借助FLAC3D数值分析软件,对地震作用下含软弱夹层顺层岩质边坡进行研究,发现振幅、频率和初动方向等对坡表放大效应影响显著,而持时对坡表放大效应影响较小。该分析借用FLAC3D建立软弱夹层顺层岩质边坡动力分析数值模型理想化的地震动输入、边界条件、网格划分与模型参数的基础上进行分析,没有考虑边坡的复杂性。高野秀夫[12]研究认为:边坡对地震波具有高程放大效应;当边坡坡角大于15°时,在地震荷载下边坡最大位移坡顶相当于坡脚的7倍。言志信[13]采用有限差分法,分析了竖直方向及水平方向在地震耦合作用下的动力响应。但没有进行试验,无法将数值模拟结果和试验结果相对照。刘强[14]通过分析场地条件,地表倾角,地震烈度等因素对地震场地的影响,得出不同场地条件下加速度反应谱表现出不同的特点。上述成果为进一步研究提供良好的基础,但由于理论计算与岩质边坡岩体结构和动力问题的复杂性,利用大型振动台试验对边坡的地震动力响应问题的研究还需不断发展和完善。
本文通过不同坡面形态的岩质边坡振动台试验,输入不同的地震动参数的地震波,监测不同地震荷载作用下的不同坡面形态、坡内坡表以及不同高程点的加速度响应值,分析监测的加速度数据,研究坡面形态和荷载的参数对加速度动力响应的影响。
1 典型工程边坡调查
以滇西南地区大保和保龙高速公路为依托,通过大量的野外边坡调查,得到了红层软岩边坡的一些基本特征。
1.1 岩性组合
红层软岩地区的岩性主要以泥岩等软岩为主,同时夹有砂岩等硬岩成分,有些岩体是由软岩硬岩互层形成的复杂岩性组合。图1给出常见的岩性组合边坡简图,软硬互层边坡。岩体上部和底部为紫红色泥岩,中间为灰绿色砂岩,岩体表面被风化层覆盖。

图1 软硬互层组合边坡简图Fig.1 Combination of soft and hard interbedded slope
1.2 岩体结构特征
原生软弱层面和软弱夹层经过多次地质构造作用后相互错动、构造结构发育及地下水的长期作用,使原生软弱层面和软弱夹层构造不断产生变化,一部分形成了泥化夹层,另一部分形成切层软弱层,这些软弱夹层结构面对边坡稳定性起至关重要的控制作用。
1.3 坡面状态
边坡按坡面几何形状一般可分凹型、凸型、斜坡3类。保龙高速公路沿线比较典型的边坡坡面状态,凹坡上部倾角较大,属于陡倾边坡岩体,下部坡率舒缓。整个坡面生态防护完好,大部分坡面被茂盛的植被覆盖,岩体由锚杆框架梁护坡。凸坡上部坡面倾斜,下部几乎属于直立边坡岩体。生态防护一般,上部灰浆护坡,边坡坡面的风化岩石剥落、碎落并伴有少量落石掉块等现象发生;下部采用挡墙支护,一方面起防护的作用,另一方面又起加固坡体的作用。
2 振动台模型箱设计
本次试验装置为西安建筑科技大学结构工程与抗震教育部重点实验室2.2×2 m单向双自由度振动台,最大试件重量为40 kN,最大加速度±27.7 m/s2,振动台波型SIN、随机、地震波,最大振幅为±100 mm。
2.1 模型试验相似关系
确定相似关系常用的方法为量纲分析法和方程分析法。本文基于π定理,采用量纲分析法导出相似判据。因模型的复杂性,很难满足所有参数相似性,需根据试验目的和模型的特性选择主控制参数,作为基本量纲进行量纲分析。本试验以几何长度,密度和加速度为基本量纲,通过推导得振动台模型试验相似常数见表1。
表1 模拟试验相似常数
Tab.1 Similarity codfficients of model test
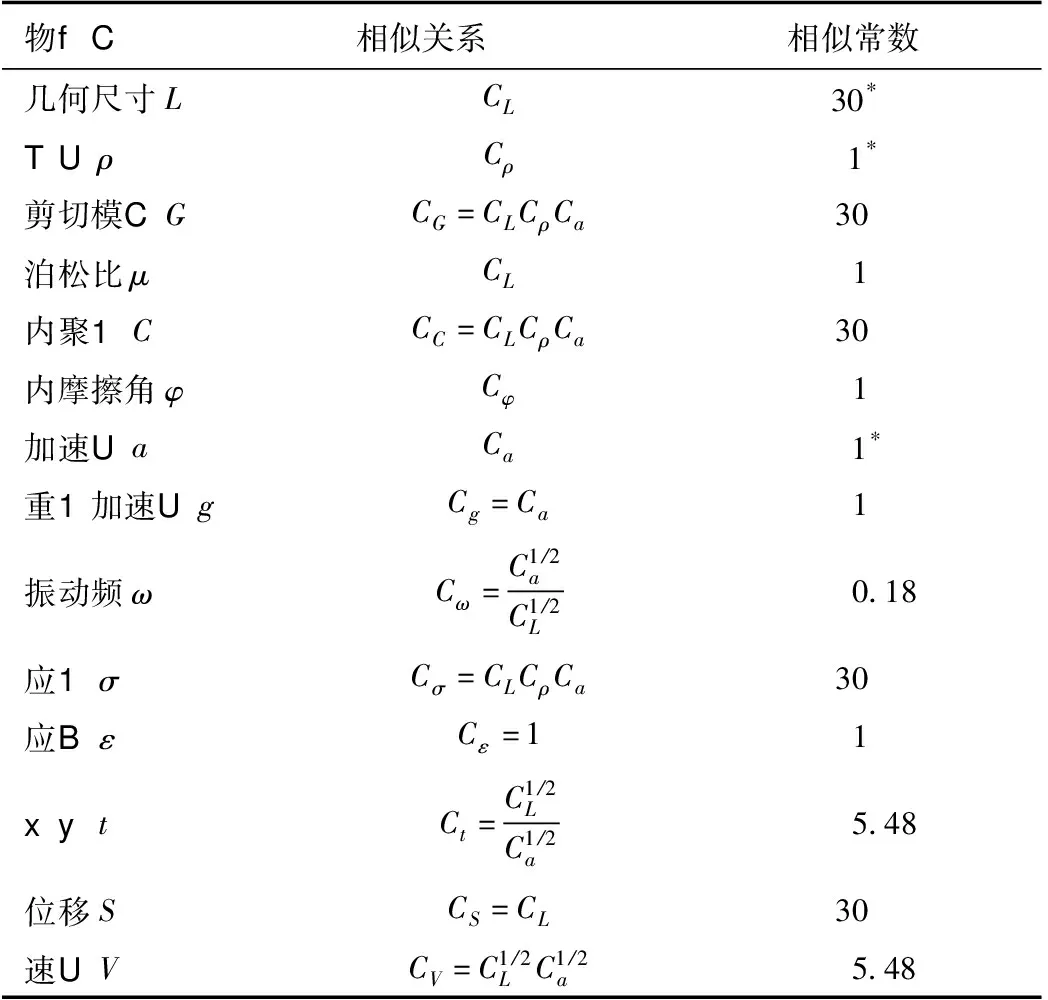
物理量相似关系相似常数几何尺寸LCL30*密度ρCρ1*剪切模量GCG=CLCρCa30泊松比μCL1内聚力CCC=CLCρCa30内摩擦角φCφ1加速度aCa1*重力加速度gCg=Ca1振动频ωCω=C1/2aC1/2L0.18应力σCσ=CLCρCa30应变εCε=11时间tCt=C1/2LC1/2a5.48位移SCS=CL30速度VCV=C1/2LC1/2a5.48
注:带*号为基本量纲。
2.2 材料选取
根据相似原理,设计选用的模型材料与原型材料密度相同,通过直剪、三轴试验确定材料参数,确定试验模型的质量配合比为重晶石粉∶石英砂∶石膏粉∶水按照32∶56∶9∶8制作边坡模型。试验证明,该配合比能够满足模型与原型之间的相似比例,可较好地满足各项物理力学参数指标要求。表2为泥岩及相似材料的主要物理力学参数指标。
2.3 监测布置与加载方案
试验采用刚性模型箱外部尺寸长宽高为1.94 m×1.3 m×1.1 m。模型箱在后壁加衬5 cm厚泡沫垫层以减小模型箱边界效应。中间采用木质挡板使两个模型分开,且挡板与箱体用角钢和螺栓固定,挡板采用防水光滑木质材料。模型各参数为:凸、凹坡尺寸1.2 m×0.65 m×1 m;均采用1∶0.5和1∶1两个坡率;坡顶宽度0.4 m;模型坡体内设置4层泥化夹层界面,距离箱底分别为0.2,0.5,0.7,0.9 m;坡脚台阶高度为0.15 m,为了增加模型稳定性,台阶铺满整个模型箱压实至箱壁。试验采用的传感器为加速度传感器和位移传感器,考虑到试验条件以及避免破坏模型完整性等因素,本次试验共布设了18个加速度传感器和4个位移传感器。其中16个加速度传感器A1~A16按照图2对称分布于两个模型中,位移传感器S1和S2粘贴于坡顶表面,加速度传感器A0′和位移传感器S0′粘贴在模型箱顶,加速度传感器A0和位移传感器S0设置在振动台台面上。其中加速度传感器A0、A0′和位移传感器S0、S0′在相同布设位置。传感器A15和A16分别埋置在凹型、凸型边坡坡体内部,距离箱壁10 cm,距离箱底30 cm。传感器A1,A7,A13布置在凹坡同一垂直线上,距离箱壁20 cm处,传感器A3,A9,A14同样布设在凸坡对应测点。
试验加载方案:依托工程滇西南地区抗震设防烈度为Ⅶ~Ⅸ,根据《建筑抗震设计规范》[15]抗震设防烈度及基本地震加速度设计值对应关系,设计试验加载方案加速度峰值0.1g,0.2g,0.3g,0.4g几个等级与设防烈度相对应,并且又增加了 0.6g,0.8g和1.0g3种加载工况。考虑到SIN波的破坏强度较大,只采用了不同频率的0.1g和0.3g两种加速度峰值。白噪声是测量模型结构动力特性的重要手段,为了解模型在激振前后的动力特性的变化,本试验在所有激振开始之前及之后的不同阶段均施加白噪声扫频。由于地震动强度较大时,SIN波对模型的破坏作用可能大于同等强度下的天然波,所以在施加完0.1g的SIN波后,接着施加几组ELCentro (ELC)波,然后再施加强度更大的SIN波。试验研究地震波振动强度、频率、类型等对岩质边坡的动力响应规律,因此采用时间压缩比为5.48的ELC波、SIN波两种波型。
2.4 模型箱自振频率分析
试验中采用的刚性模型箱具有自身的固有频率,为避免与加载的地震波频率及边坡自振频率产生共振,试验前对空模型箱进行自振频率试验,通过多组锤击试验测定本次试验采用的模型箱自振频率为43.467 Hz,远远大于试验加载方案中设计的地震波频率值及模型边坡自振频率值,符合本次试验要求。
表2 原型和模型的主要物理力学参数表
Tab.2 Physical and mechanical parameter table of prototype and model

岩性密度ρ/(g·cm-3)剪切模量G/MPa泊松比内聚力c/kPa内摩擦角φ/(°)红层软岩(泥岩)原型2.4719000.353224.04相似材料模型2.463.30.317.324.5

图2 模型边坡传感器布置图Fig.2 Sensor layout of model slopediagram
2.5 模型箱边界效应分析
振动台模型试验中,由于模型土体要完全放置在模型箱中,与之接触的箱壁边界必然会对模型产生影响[16]。在地震荷载作用下,输入的地震波经土体传播,会在箱壁产生一系列的反射和折射,给试验结果造成一定的影响。通过试验埋设的特殊测点对边界效果进行检验。以ELC-1工况下,埋设距箱底20 cm测点A2与台面测点A0为例,从图3中可以看出,相对于台面测点A0,测点A2加速度峰值有明显放大。由此可得出模型土体与箱底边界接触比较良好,摩擦边界效果能够满足试验要求。

图3 测点A2与A0加速度时程曲线对比图Fig.3 Comparison of acceleration time history curvesbetween measuring point A2 with measuring point A0
2.6 边坡模型模态参数分析
对于振动台模型试验动力信号处理,模态参数分析是十分重要的一部分,目的是从所得的信号中,确定振动系统的模态固有频率、模态阻尼比等模态参数。原理是输入用于扫频的白噪声波,通过坡体的反馈使输入信号发生畸变,以各测点的加速度信号对台面的加速度信号作传递函数[17],得到结构的主振频率、阻尼比以及振型等。在试验中根据加载方案,采用幅值0.05g的白噪声进行激励,通过埋置测点加速度响应时程,得到其频率响应函数,通过模态参数识别技术可以得到边坡模型的自振频率、阻尼比等动力特性。以凸坡为例各工况白噪声激励后凸型边坡坡内测点模态参数见表3,其变化趋势见图4。得出:同一工况下不同测点的自振频率与阻尼比相同,说明边坡模态参数与高程无关,随着白噪声工况的逐级加载,可发现模型体系的一阶自振频率逐渐降低,阻尼比逐渐增加,产生该现象的原因是在振动激励下岩土体的动剪切强度和动剪切模量下降,非线性特征加强。
表3 凸型边坡坡内测点第一阶模态参数
Tab.3 First order modal parameters obtained from measuring points in convex slope
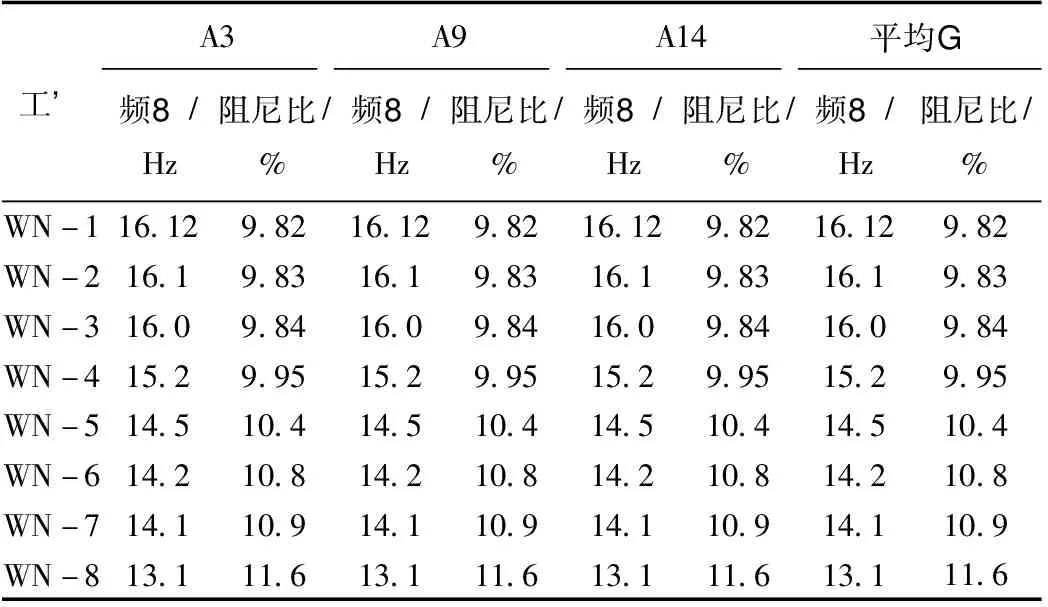
工况A3A9A14平均值频率/Hz阻尼比/%频率/Hz阻尼比/%频率/Hz阻尼比/%频率/Hz阻尼比/%WN-116.129.8216.129.8216.129.8216.129.82WN-216.19.8316.19.8316.19.8316.19.83WN-316.09.8416.09.8416.09.8416.09.84WN-415.29.9515.29.9515.29.9515.29.95WN-514.510.414.510.414.510.414.510.4WN-614.210.814.210.814.210.814.210.8WN-714.110.914.110.914.110.914.110.9WN-813.111.613.111.613.111.613.111.6

图4 模型体系模态参数变化趋势Fig.4 Modal parameter variation trends of model system
3 地震边坡动力响应特征分析
边坡变形破坏的主要因素是地震惯性力,该地震惯性力和加速度有关。本次试验主要研究模型边坡加速度、速度和位移响应规律。考虑到位移传感器质量较大,无法埋置到模型边坡坡体中等原因,试验中埋置测点均为加速度传感器,因此速度和位移时程曲线均根据加速度时程曲线积分得到。
3.1 加速度动力响应
PGV放大系数和PGD放大系数同PGA放大系数一样,定义为模型中某一测点响应加速度峰值与台面测点加速度峰值的比值。从各测点加速度时程曲线看出,相对于台面测点坡体上各测点的峰值加速度均有不同程度的放大,从台面到各测点的傅氏谱可以发现,模型边坡对高频段的地震波存在滤波作用,对低频段的地震波存在放大作用。对比台面测点发现,坡体埋设的测点峰值加速度均有不同程度的放大。ELC工况输入的加速度幅值分别为0.1g,0.2g,0.3g,0.4g,0.6g,0.8g,1.0g等7个等级,由表4得出在两种坡型的变坡点附近和坡肩部位加速度放大效应最为明显。以ELC-3为例,两种坡型边坡在坡肩和变坡点处加速度峰值均相对于台面增加了129%,138%和107%,139%,其他部位测点峰值加速度也有不同程度增加。
3.2 速度和位移动力响应
以幅值为0.3g的ELC-3工况为例,分析速度和位移时程曲线得出速度时程曲线和位移时程曲线,可得凸型及凹型边坡坡肩、变坡点及坡脚各测点的PGV放大系数和PGD放大系数。数据处理得到台面输入的峰值速度为6.65 cm/s,峰值位移为3.95 mm。由图5可知凸型边坡坡肩PGV放大系数达到了1.72,变坡点和坡脚均维持在1.2~1.6之间,凹型边坡坡肩PGV放大系数达到1.81,变坡点和坡脚处在1.5左右,两种坡面形态下速度动力响应都比较显著。凸型、凹型边坡从坡脚到坡肩PGD放大系数呈现递增趋势,凸坡坡肩PGD放大系数1.25,凹坡坡肩PGD放大系数1.29。对比两种坡面得出:凹型边坡速度和位移放大效应明显强于凸型边坡,从整体趋势上来看,边坡PGV和PGD放大效应均比较显著。
表4 ELC工况各测点峰值加速度(单位:m/s2)
Tab.4 Peak acceleration of each measuring point under ELC condition (unit:m/s2)

测点工况ELC-1ELC-2ELC-3ELC-4ELC-5ELC-6ELC-7台面A01.092.073.014.066.117.9610.63A41.343.174.455.358.868.7510.02A31.493.645.676.179.049.7111.81A61.804.266.268.6113.0113.2115.13凸坡A101.553.374.787.1111.3113.6111.27A91.423.04.596.3310.0814.3210.5A121.843.956.089.3714.4816.4710.78A141.863.666.899.5412.7716.7112.95A161.513.685.696.5710.049.8111.91A21.533.796.377.8311.7312.2511.92A11.513.775.986.579.8311.1411.84A51.854.037.168.8113.6216.7112.92凹坡A81.633.876.307.3110.9414.5613.66A71.53.335.416.9410.4515.211.69A111.684.166.449.2513.4417.679.21A131.883.897.199.2114.0517.0311.52A151.533.975.786.679.7811.6711.21

图5 工况ELC-3下PGV放大系数和PGD放大系数与高程的关系Fig.5 Relationship of elevation with PGV and PGDamplification coefficients under ELC-3 condition
4 边坡动力响应影响因素分析
4.1 坡面形态对边坡动力响应的影响

图6 0.3g ELC波两种坡面形态下各测点PGA放大系数Fig.6 PGA amplification coefficient obtained from eachmeasuring point in 2 slope forms under 0.3g ELC wave
以输入加速度值0.3g的ELC波和0.3g,7.5 Hz的SIN波为例。由图6得出:凸、凹坡对称测点的PGA放大系数整体相差不大。趋势是凹坡PGA放大系数要略大于对应测点的凸坡。对比分析两种坡面形态边坡模型有如下特点。相同点:两种坡面形态下PGA放大系数沿高程整体呈现放大趋势,在变坡线以下(即大致1/2高程处),两者数值上相差不大;两种坡型在变坡线附近PGA放大系数均出现急剧增大,在变坡线下一测点(高程40 cm)增幅尤为剧烈,同时在变坡线上又出现局部减小的现象;两种坡型PGA放大系数在坡肩处再次出现急剧增大趋势,在数值上明显高于其他测点。不同点:凹坡各测点PGA放大系数整体上略大于凸坡,在变坡线以上这一特点更为显著;通过PGA放大系数沿高程方向构成的曲线可以得出,凸、凹坡均以折线形式变化,而凹坡PGA放大系数构成的折线则更为复杂;主要是由于在变坡线附近出现坡率变化,在这一位置处加速度放大效应尤为显著,使得附近测点PGA放大系数陡增。分析可以得出:凹坡相对于凸坡在坡肩处(高80 cm)PGA放大效应更加明显,即凹坡坡肩处先于凸坡破坏。造成稳定差异的原因可能是凹型坡在坡面斜率突变的地方出现剪应变集中区和地震力的作用下边坡表面岩土体产生破坏,导致动荷载传递异常。
图7数据表明:两种坡型边坡PGA放大系数表现出和ELC波工况相似的规律,各测点PGA放大系数连接形成的曲线依然呈折线递增趋势;凹坡测点的PGA放大系数依然和凸坡保持平行递增趋势,相对来说表现出更加明显的放大效应。
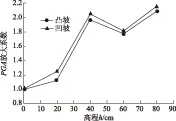
图7 0.3g,7.5 Hz的sin波两种坡面形态下各测点PGA放大系数Fig.7 PGA amplification coefficients obtained from eachmeasuring point under sine waves of 0.3g and 7.5 Hz
4.2 高程对边坡动力响应影响规律
试验中两种模型坡内和坡表分别埋设了7个对称测点,但坡表测点高程不在同一条竖直方向上,故取边坡坡内3个测点作为分析对象。取0.3gEL Centro波及频率5 Hz SIN波工况为例,图8竖直方向(高程)分析,随着高程的增加,PGA放大系数表现出递增趋势,但这种趋势呈现不同特点,变坡线以下随高程的增加加速度动力响应增强,变坡线附近(高程60 cm)左右时,个别工况PGA放大系数不增反降,原因是受到坡型,软弱夹层结构面及地震动参数的影响,高程上的这种放大效应表现出整体保持增大,特殊地理位置略有缩小的趋势。对比两种坡型边坡得出:凹坡高程放大效应更为显著。通过对PGA放大系数数据分析,得出在地震荷载作用下的“高程放大效应”是有适用条件的,当受到边坡地形条件以及地震动参数的影响这种规律呈现不同特征。
4.3 地震波类型对边坡动力响应规律的影响
试验在几种加速度幅值条件下设计了ELC波和SIN波两种地震波输入,以ELC-1,SIN-1为例见图9,通过分析凸坡坡面测点A4,A6,A12对应的PGA放大系数,发现SIN-1工况在各测点PGA放大系数明显大于ELC-1工况,得出不同的地震波作用下加速度放大效应不同,原因可能是不同的地震波其频谱特性差异很大。
4.4 振动强度对边坡动力响应规律的影响
试验设计了两种地震波形不同加速度幅值的地震动输入方案,ELC波工况下加速度幅值分为0.1g,0.2g,0.3g,0.4g,0.6g,0.8g等6个等级,SIN波工况下加速度幅值为0.1g和0.3g的激振试验。
由图10和图11可知在小幅值(0.1g~0.3g左右)PGA放大系数呈现增大趋势,个别测点有小幅波动;幅值在0.4g~0.6g之间基本保持稳定,幅值超过0.6g后又出现递减趋势。具体分析为:凸坡坡内测点A3在幅值0.1g~0.3gPGA放大系数小幅增加,随后急剧减小,且幅度较大;测点A9、A14基本保持先增加再稳定后减小趋势。坡表测点PGA放大系数整体呈现前期小幅波动并保持增大,后期逐渐减小趋势。凹坡坡内测点在幅值0.1g~0.3gPGA放大系数逐渐增大,A13测点增幅最大,后期各测点PGA放大系数均逐渐减小,A1测点减小趋势最为显著,减小幅度也较大;坡表各测点同样呈现出上述特点,即0.1g~0.3g左右PGA放大系数逐渐增大,之后保持稳定,最后减小。分析得出,随着地震动幅值的增大,边坡测点PGA放大系数大致呈现先增大再稳定后减小的趋势。原因可能为台面输入的加速度幅值越大,动应力水平就会越高,从而剪切模量就会越低,阻尼比增大,边坡土体的隔震减震作用就会越强。董金玉在地震作用下顺层岩质边坡动力响应和破坏模式大型振动台试验研究中得出相同的结论。
4.5 地震频率对动力响应规律的影响
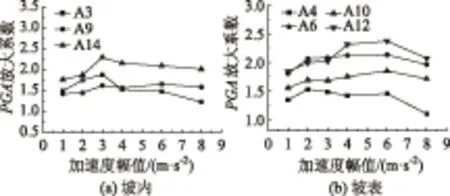
图10 凸型边坡PGA放大系数与加速度的关系Fig.10 Relationship between PGA amplification factor and acceleration of convex slope
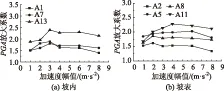
图11 凹型边坡PGA放大系数与加速度的关系Fig.11 Relationship between PGA amplification factor and acceleration of concave slope
根据地震动力学原理:荷载频率与边坡坡体的固有频率相同时,边坡将会发生共振现象[18]。本试验根据傅立叶频谱分析找到了模型边坡的自振频率,且试验之前对模型箱做了自振试验分析,为合理选择试验工况中的频率提供了依据。
试验加载方案设计SIN波频率5,7.5,10,12.5 Hz等工况分析地震动参数中的频率对边坡动力响应规律的影响。
图12为加速度幅值0.1g不同频率SIN波各测点PGA放大系数随频率变化曲线可知,凸坡坡内不同高程测点PGA放大系数表现出了不同的变化特点,随着地震频率的增加,A9和A14测点PGA放大系数表现增大趋势,A3测点先保持平稳后急剧增大;坡表测点A4和A12的PGA放大系数持续缓慢增大,后期增加幅度较大,A6和A10测点PGA放大系数随着频率增大表现先急后缓,随着频率增大整体依然表现为增大趋势。

图12 凸型边坡PGA放大系数与频率的关系Fig.12 Relationship between PGA amplification coefficient and frequency of convex slope
图13加速度幅值0.1g不同频率SIN波工况下各测点PGA放大系数与频率的关系可知凹坡坡内不同高程测点PGA放大系数随着地震频率的增加整体上表现增大趋势;坡表测点A2和A11的PGA放大系数持续缓慢增大,A5和A8测点PGA放大系数随着频率增大表现出折线递增趋势,在频率为10 Hz左右出现小幅减小,之后随着频率增大而继续增加。

图13 凹型边坡PGA放大系数与频率的关系Fig.13 Relationship between PGA amplification coefficient and frequency of concave slope
5 结论
通过振动台模拟试验对边坡动力特征,加速度、速度、位移动力响应规律进行研究,并对动力响应影响进行了深入分析,得出以下结论:
(1)对模型箱自振频率分析得出模型箱自振频率远大于试验加载频率及边坡模型频率,符合试验要求。
(2)凸、凹坡对称测点的PGA放大系数整体相差不大。趋势:凹坡PGA放大系数略大于对应测点的凸坡。坡型对边坡加速度动力响应有影响,但不显著,凹坡较凸坡不稳定。
(3)坡表测点PGA放大系数始终大于坡内,趋表效应显著。坡内、坡表测点PGA放大系数呈折线递增,表现非线性特征;高程放大效应显著,但受到边坡地形条件及地震动参数的影响这种规律呈现出一定的特点。
(4)地震波类型对边坡动力响应影响显著,不同的地震波其频谱特性差异很大,导致加速度放大效应不同,同一幅值SIN波加速度放大效应较ELC波明显。
(5)随幅值增加,加速度峰值放大系数先增加再稳定后减小。随频率增加,加速度动力响应呈现出非线性变化;频率在一定范围增加时,频率越高动力放大效应越显著,与边坡自振频率密切相关。
[1] 张立,付宏渊,付康林,等. 汶川地震诱发边坡动力失稳影响因素分析[J].公路交通科技,2011,28(4):12-18. ZHANG Li,FU Hong-yuan, FU Kang-lin, et al. Analysis on Influencing Factors of Slope Dynamic Stability Induced by Wenchuan Earthquake[J].Journal of Highway and Transportation Research and Development,2011, 28(4): 12-18.
[2] BOUCKOVALAS G D, PAPADIMITRIOU A G. Numerical Evaluation of Slope Topography Effects on Seismic Ground Motion[J]. Soil Dynamics & Earthquake Engineering, 2005, 25(7-10):547-558.
[3] ZHANG C H,PEKAU O A, JIN F, et al. Application of Distinct Element Method in Dynamic Analysis of High Rock Slope and Blocky Structures [J].Soil Dynamics and Earthquake Engineering,1997,16(4):385-394.
[4] KIM D, PAN X, PARDALOS P M. An Enhanced Dynamic Slope Scaling Procedure with Tabu Scheme for Fixed Charge Network Flow Problems[J]. Computational Economics, 2006, 27(27):273-293.
[5] 徐光兴, 姚令侃, 高召宁,等.边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学工程学报, 2008, 27(3): 624-632. XU Guang-xing,YAO Ling-kan,GAO Zhao-ning,et al. Large-scale Shaking Table Model Test Study on Dynamic Characteristics and Dynamic Responses of Slope[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(3):624-632.
[6] 徐光兴, 姚令侃, 李朝红, 等. 边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报, 2008, 30(6): 918-923. XU Guang-xing,YAO Ling-kan,LI Zhao-hong,et al. Dynamic Response of Slopes under Earthquakes and Influence of Ground Motion Parameters[J].Chinese Journal of Geotechnical Engineering,2008,30(6):918-923.
[7] 徐光兴.地震作用下边坡工程动力响应与永久位移分析 [D]. 成都:西南交通大学, 2010. XU Guang-xing. Research on Dynamic Response and Permanent Displacement of Slope under Earthquake [D]. Chengdu: Southwest Jiaotong University,2010.
[8] LIN Mei-ling, WANG Kuo-lung. Seismic Slope Behavior in a Large-scale Shaking Table Model Test [J]. Engineering Geology,2006, 86(2): 118-133.
[9] 许强, 陈建君, 冯文凯, 等. 斜坡地震响应的物理模拟试验研究[J]. 四川大学学报:工程科学版,2009, 41(3): 266-272. XU Qiang,CHEN Jian-jun,FENG Wen-kai,et al. Experimental Study of the Seismic Response of Slopes by Physical Modeling [J]. Journal of Sichuan University:Engineering Science Edition,2009,41(3):266-272.
[10]许强,刘汉香,邹威, 等.斜坡加速度动力响应特性的大型振动台试验研究[J].岩石力学与工程学报, 2010,29(12): 2420-2428. XU Qiang,LIU Han-xiang,ZOU Wei,et al. Large-scale Shaking Table Test Study of Acceleration Dynamic Responses Characteristics of Slopes [J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(12): 2420-2428.
[11]冯志仁, 刘红帅,于龙. 地震作用下含软弱夹层顺层岩质边坡表面放大效应研究[J]. 防灾减灾工程学报,2014,34(1):96-100. FENG Zhi-ren,LIU Hong-shuai,YU Long. Surface Amplification Effect of Bedding Rocky Slope with Weak Interlayer under Earthquake[J]. Journal of Disaster Prevention and Mitigation Engineering,2014,34(1): 96-100.
[12]周红燕.边坡地震响应及动力稳定性分析[D].成都:西南交通大学,2013. ZHOU Hong-yan. Research on Seismic Response and Dynamical Stability of Slope[D]. Chengdu: Southwest Jiao Tong University, 2013.
[13]言志信, 高乐, 彭宁波,等. 顺层岩质边坡地震动力响应研究[J]. 岩土力学, 2012, 33(增2): 85-90. YAN Zhi-xin,GAO Le,PENG Ning-bo,et al. Study of Dynamic Response of Bedding Rock Slope under Earthquakes [J]. Rock and Soil Mechanics,2012,33(S2):85-90.
[14]刘强.地震场地响应分析及大型振动台试验研究[D].成都:西南交通大学,2013. LIU Qiang. Seismic Site Response Analysis and Large-scale Shaking Table Test[D]. Chengdu: Southwest Jiaotong University, 2013.
[15]GB50011—2010, 建筑抗震设计规范[S]. GB50011—2010,Code for Seismic Design of Buildings[S].
[16]李金贝,张鸿儒,李志强.高烈度地震区公路填方路基大型振动台模型试验[J].公路交通科技,2011,28(11):1-6. LI Jin-bei,ZHANG Hong-ru,LI Zhi-qiang. Large-scale Shaking Table Model Test for Fill Subgrade of Highway in High-intensity Earthquake Area[J]. Journal of Highway and Transportation Research and Development, 2011,28(11):1-6.
[17]任自铭. 地震作用下斜坡动力响应及稳定性研究[D].成都:西南交通大学,2007. REN Zi-ming. Dynamic Response and Stability of Slope under Seismic Excitations[D].Chengdu: Southwest Jiaotong University,2007.
[18]汪茜.地震作用下顺层岩质边坡变形破坏机理研究[D].长春:吉林大学, 2010. WANG Xi. Study on Deformation Characteristics and Failure Mechanism of Bedding Rock Slope under Earthquake[D].Changchun:Jilin University,2010.
Shaking Table Model Test of Slope Seismic Dynamic Response
MA Xiao-li1, YAN Kun-fa2,LIU Xiao-yan2,PENG Yong-tao2,XU Guan-jun2
(1.Yulin University, Yulin Shaanxi 719000, China; 2. Key Laboratory for Special Area Highway Engineering of Ministry of Education, Chang’an University, Xi’an Shaanxi 710064, China)
To study the influence of slope position and ground motion parameters on dynamic response of acceleration, through the shaking table model test, the slope dynamic responses of different slope type are analysed, the influences of slope shape, elevation, type of seismic wave, vibration intensity, earthquake frequency on dynamic response are revealed. The experimental result shows that (1) the modal parameters of slope are independent of elevation, and the first order natural frequency of the model system reduces gradually and the damping ratio increases gradually as the white noise increases gradually; (2) the acceleration amplification factor of measuring point on concave slope is slightly larger than that on convex slope, the stability of convex slope is better than concave slope; (3) under seismic load, the elevation amplification effect affected by slope topography and ground motion parameters is different, the elevation amplification effect of the concave slope is more significant than the convex slope; (4) the acceleration amplification coefficient obtained from each measure point at slope surface and inner slope shows a trend of increasing fold line, but the acceleration amplification coefficient of each measuring point of slope surface is greater than that of inner slope; (5) slope dynamic amplification effect is closely related to the natural frequency of slope, in certain range, the higher the frequency, the more significant the amplification effect; (6) along the height direction, the impact of vibration strength on the slope dynamic response distribution is little, but the impact on the slope acceleration amplification effect is obvious.
road engineering;amplification coefficient of acceleration;shaking table model test; slope dynamic response;earthquake
2015-11-12
交通运输部科技项目(2008353361420)
马小莉(1967-),女,陕西绥德人, 硕士,副教授.(zzb@yulinu.edu.cn)
10.3969/j.issn.1002-0268.2016.11.006
P642.22
A
1002-0268(2016)11-0034-08

