变荷载下双层不排水桩复合地基一维固结分析
赵明华,吴岳武,郑 玥
(湖南大学 土木工程学院,湖南 长沙 410082)
变荷载下双层不排水桩复合地基一维固结分析
赵明华,吴岳武,郑 玥
(湖南大学 土木工程学院,湖南 长沙 410082)
假定弱排水桩复合地基中的桩体不排水,同时考虑地基土的成层性与荷载随时间任意变化两个条件,导出了变荷载下双层不排水桩复合地基的一维固结控制方程,得到了此类地基中超静孔隙水压力的一般解析解,并给出了瞬时加载和单级等速加载两种常见情况下超静孔隙水压力和固结度的解答;然后,通过将本文解退化为经典解和与算例分析两种途径验证了本文解析解的合理性;最后,利用编程计算分析了双层不排水桩复合地基的固结规律。结果表明:随着桩径比的减小、桩体刚度的增大和加荷速率的增大,固结速率会增大;kv2/kv1越大,E2/E1越大,h2/h1越小,则固结越快;分别按平均孔压和按沉降定义的双层不排水桩复合地基固结度会有差别,差别大小与各层土体的压缩模量有关。
道路工程; 复合地基;不排水桩;固结;双层;变荷载
0 引言
采用弱排水桩作为竖向增强体的复合地基法是软土地基处理中的主要方法之一,例如水泥土搅拌桩复合地基和灰土桩复合地基等,已被广泛应用于工程实践中。与粗砂、碎石等散体材料不同,水泥土、灰土等属于胶凝材料,胶凝材料的渗透性很小,在设计计算中一般予以忽略。研究表明[1],水泥土搅拌桩的渗透系数可达到10-8~10-9cm/s数量级,通常比桩周软土的渗透系数低1~3个数量级。因此,在分析弱排水桩复合地基的固结问题时,可简化地将水泥土搅拌桩、灰土桩等胶凝材料桩视为不排水桩,即不考虑桩的渗透性,以期获得解析解。
目前,关于砂桩、碎石桩等散体材料桩复合地基的固结理论已有较深入的研究,获得了能够考虑变荷载、地基成层和涂抹作用、桩未打穿以及半透水边界等较为复杂条件下的固结解析解[2-5]。但迄今为止,不排水桩复合地基的固结理论研究则较少。杨涛等[6-8]将真实的非均质复合土体替代为等价均质复合土体,采用复合模量法对变荷载下不排水桩复合地基的固结问题进行了研究,但此方法缺少严格的理论推导;卢萌盟等[9]证明了不排水桩复合地基只会产生竖向渗流,获得了瞬时加载和单级加载两种情况下的单层不排水端承桩复合地基的一维固结解析解,但此理论没有给出其他加载条件下的解析解;杨涛等[10]研究了当软土地基较厚时复合地基分为上层加固区与下卧层的情况,给出了瞬时加载条件下不排水悬浮桩复合地基固结计算的解析公式,随后,龚晓南等[11]导出了线性加载条件下不排水悬浮桩复合地基固结计算的简化公式,发展了不排水桩复合地基固结理论。目前已提出的不排水桩复合地基固结计算模型,考虑了荷载线性施加和桩体悬浮,但没有考虑地基土的成层性,而实际工程中,常会遇到桩体穿越成层软土地基而嵌入持力层的情况,这便涉及成层不排水桩复合地基的固结度计算问题。在计算成层地基的固结度时,常将成层的非均质地基替代为均质地基,再利用太沙基一维固结公式计算,然而,采用这种加权平均的简化计算方法一般难以得到合理结果[12],因此,在建立固结计算模型时应考虑地基土的成层性。成层地基的固结理论研究历来受国内外岩土工程界所关注,经过众多学者多年研究,目前已有较多有关成层天然地基、成层砂井地基和成层散体材料桩复合地基固结理论的有益成果[12-15],但迄今尚缺少关于成层不排水桩复合地基固结问题的解析解。另外,实际工程中复合地基上部荷载并不是瞬时施加,有必要根据实际工程的加载曲线,在复合地基固结分析中考虑施工荷载随时间任意变化条件。
为此,本文拟在前人的研究基础上,假定弱排水桩复合地基中的桩体不排水,同时考虑变荷载和地基土的成层性,研究了变荷载下双层地基中不排水桩复合地基(简称双层不排水桩复合地基)的固结问题,在证明此类双层地基系统正交公式的基础上,获得了其解析解答,并通过将本文解退化为经典解和算例分析两种途径验证了本文解析解的正确性,以期为施工时间控制和工后沉降控制提供一些指导。
1 固结模型的建立与分析
1.1 计算模型
图1为变荷载下双层不排水桩复合地基固结模型。其中,hi,kri(r),kvi和Ei分别为土层i(i=1、2,分别表示上、下层)的厚度、径向渗透系数、竖向渗透系数和复合压缩模量,Ec为桩体压缩模量,H为双层地基总厚度,rc,rs和re分别为桩体、扰动区和影响区半径;q(t)为大面积均布荷载,可随时间任意变化。其排水条件为地基顶面透水,底面不透水。

图1 双层不排水桩复合地基固结模型Fig.1 Consolidation model of double-layered compositefoundation with impervious pile
本文采用如下假定:
(1)等应变条件成立,即桩体与土体均受侧向约束,并且任意深度处竖向变形相等;
(2)土体完全饱和,土体中水的渗流规律服从达西定律;
(3)复合地基中的桩体不排水;
(4)所加荷载随时间任意变化;
(5)在任意时刻两层交界处的竖向渗透速率和孔隙水压力处相等。
1.2 固结方程
对上述模型,由平衡条件、等应变假设和桩体不排水假设可得
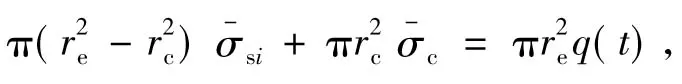
(1)

(2)

由式(1)和(2)可得:
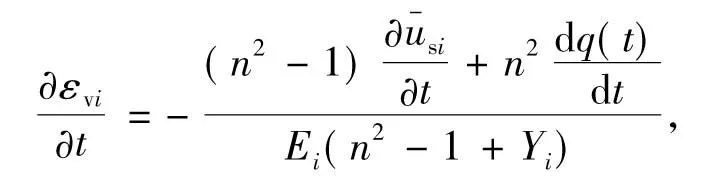
(3)

土体内径竖向渗流的固结方程为[9]

(4)
式中,usi为土体内任一点处的超静孔隙水压力;γw为水的重度。
其边界条件、连续条件和初始条件分别为
边界条件:

(5)
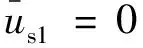
(6)
连续条件:
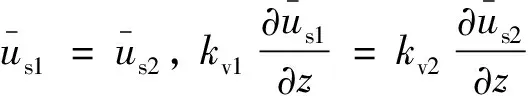
(7)
初始条件:

(8)
式中,σ0为土体内的初始孔压。
利用边界条件式(5),参考文献[9],可推导得到变荷载下双层不排水桩复合地基的一维固结控制方程为
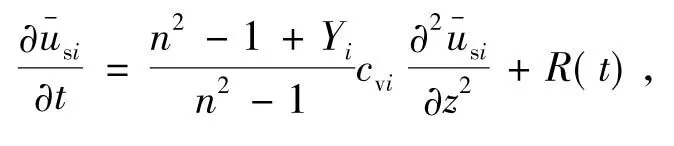
(9)
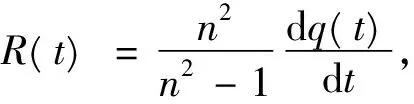
1.3 方程求解
首先,定义无量纲参数如下:
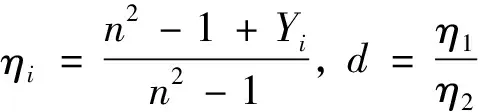
[10],设式(9)的解形式如下:

(10)
(11)
式中,βm,μ,λm,Am,Bm和Cm均为待定系数;Tm(t)项由式(9)中的R(t)项引起,为时间t的待定函数。
式(10)、(11)显然满足边界条件式(6),将式(10)、(11)代入连续条件式(7)可得

(12)
式(12)也可以转化为
μasin(μcλm)sin(λm)-cos(λm)cos(μcλm)=0,
(13)
式(13)即为确定特征值λm的特征方程。式(13)为超越方程,不能直接求解,可采用二分法编程求解。
再将式(10)、(11)代入式(9),可得

(14)
以及待定系数Cm应满足方程

(15)
类似于成层散体材料桩复合地基固结理论中的正交证明[15],可证明双层不排水桩复合地基的正交关系式在形式上与双层散体材料桩复合地基固结理论的一致(证明略):

(16)
利用式(15)和正交关系式(16)可得
(17)
最后由初始条件式(8)有
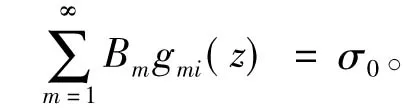
(18)
用确定Cm的同样方法可得
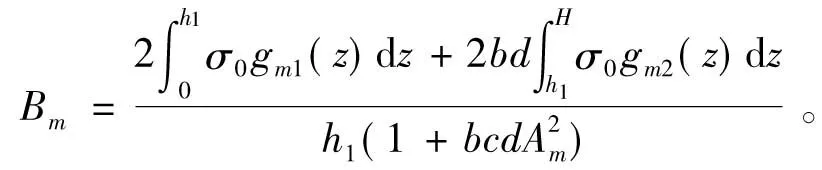
(19)
现已求出所有待定系数,可写出满足一切求解条件的变荷载下双层不排水桩复合地基的一般解答为:

(20)
代入荷载条件后,即可求得双层不排水桩复合地基在不同加载条件下的固结解答。限于篇幅,本文仅给出瞬时加载和单级等速加载两种常见情况下的解答,以供参考。
(1)瞬时加载情况下的解答
图2为本文研究的两种情况下的荷载施加曲线。如果荷载为瞬时施加时,σ0=n2qu/(n2-1), q(t)=qu, R(t)=0,由一般解答式(20),可得瞬时加载情况下双层不排水桩复合地基固结解为
(21)

(2)单级等速加载情况下的解答
如图2(b)所示,如果荷载为单级等速施加,则初始孔压σ0=0,且

(22)
将式(22)代入一般解答式(20),可得单级等速加载情况下双层不排水桩复合地基固结解为:
加载阶段(0≤t≤tc):

(23)
竣工后(t≥tc):
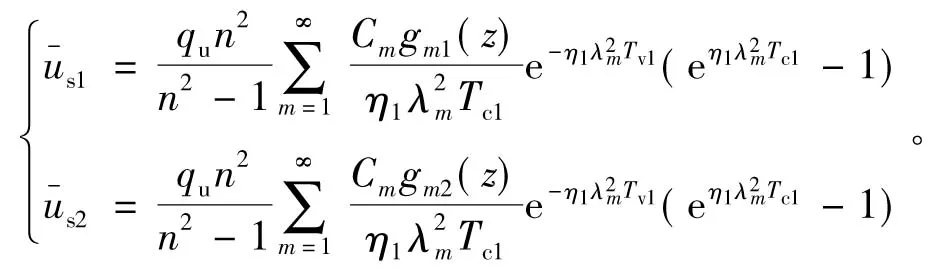
(24)
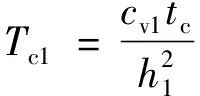
如果令tc→0,式(23)和式(24)即退化为瞬时加载情况下的固结解表达式(21)。
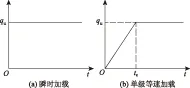
图2 荷载施加曲线Fig.2 Curves of loading
1.4 固结度计算
地基的平均固结度可按沉降定义和按平均孔压定义[16],当地基为双层时,其计算公式分别为

(25)

由式(1)、(2)可得

(26)
当t→∞时,由式(26)可得土体内最终平均总应力为
(27)
将式(26)、(27)代入式(25),可得

(1)瞬时加载情况下的平均固结度
将式(21)分别代入式(28)、(29),可得瞬时加载情况下双层不排水桩复合地基的平均固结度为

(30)

(31)

(2)单级等速加载情况下的平均固结度
将式(23)、(24)分别代入式(28)、(29),可得单等速加载情况下双层不排水桩复合地基的的平均固结度为

(32)

(33)
最后,对固结度解析解表达式(30)~(32)和(33)进行了讨论:
(1)当地基为单层天然地基时有
a=b=d=1,c=0,且n→∞,
(34)
则
(35)
将式(34)代入式(13)可以求得

(36)
最后,将式(35)、(36)代入式(30)、(31)可求得

(37)
因此,本文解可退化为经典的太沙基一维固结解。
(2) 同理,当地基为双层天然地基时,即当d=1,n→∞时,本文解可退化为双层天然地基固结解[12]。
(3) 同理,当地基为单层不排水桩复合地基时,即当a=b=d=1且c=0时,本文解可退化为单层不排水桩复合地基固结解[9]。
2 算例验证
杨涛等[6-8]将非均质复合地基替代为等价均质复合土体,采用复合模量法研究了不同加载条件下单层不排水桩复合地基的固结问题。该法采用提出的复合模量公式计算等价均质复合土体的模量后,再运用太沙基一维固结公式计算均质复合土体的固结度,其解答与有限元解具有较好的一致性。本文拟将获得的双层不排水桩复合地基固结解析解与文献[6-7]的解答进行对比验证,以期反映本文解析解的合理性。
由于目前鲜有关于双层不排水桩复合地基固结问题的研究成果,在利用本文方法计算文献[6、7]中单层不排水桩复合地基固结度时,人为地将单层地基划成双层地基,并且上、下层地基土参数均相同,即a=b=d=1,h1,h2可任意取值并满足H=h1+h2。
本文的参数与文献[6-7]的参数取值相同,如表1所示。其中,当荷载为大面积瞬时施加时,q0=100 kPa;当荷载为单级等速施加时,tc=12 d,荷载为大面积4 m厚填土。边界条件为地基顶面透水,底面不透水。

表1 算例参数取值一览表Tab.1 List of parameter values in calculation example
图3给出了瞬时加载时不同桩土模量比情况下的两种方法获得的复合地基固结度随时间变化的比较曲线。图3表明,本文解析解与文献[6]解有很好的一致性。

图3 瞬时加载时复合地基固结度比较Fig.3 Comparison of consolidation degrees of compositefoundation under instantaneous loading
图4给出了单级等速加载情况下本文方法和文献[7]的复合模量法获得的低透水桩复合地基固结度随时间变化的比较曲线。图4表明,单级等速加载条件下,本文方法获得的固结度与文献[7]的复合模量法获得的固结度也具有很好的一致性。

图4 单级加载时复合地基固结度比较Fig.4 Comparison of consolidation degrees of compositefoundation under single-stage loading
文献[6-7]中基于等价均质土体的复合模量法可以认为是一种经验方法,而本文解析解有严格的理论推导,更能反映固结的本质规律。另外,本文计算模型不仅可以计算双层不排水桩复合地基的固结问题,也可以计算单层不排水桩复合地基的固结问题与双层天然地基的固结问题,因此,本文方法更具普遍适用性。
3 参数分析
本文通过编程计算,探讨了双层不排水桩复合地基固结的一般规律。由本文解析解可以看出,双层不排水桩复合地基固结计算主要取决以下无量纲参数:a=kv2/kv1,c=h2/h1,Y1=Ec/E1,Y2=Ec/E2,n和加载时间t,本文对以上参数进行了探讨。此外,还将分别按沉降和按平均孔压定义的固结度曲线进行了比较。各图计算参数的取值见表2,表中,tc=0代表荷载瞬时施加,E1=3 MPa,h1=10 m,k1=10-6cm/s,图5~图9中的总平均固结度均按平均孔压定义。
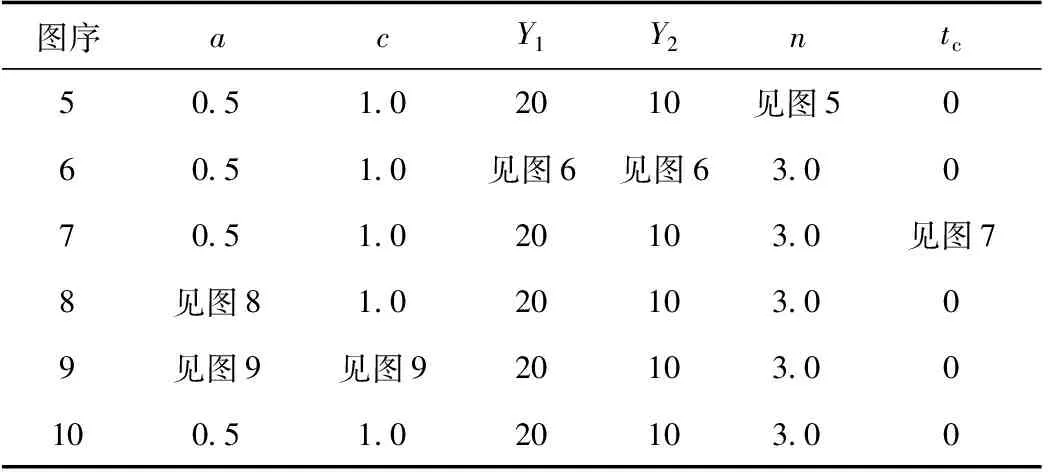
表2 各图计算参数取值一览表Tab.2 List of parameter values in each figure

图5 桩径比对固结过程的影响 Fig.5 Influence of pile-diameter ratio on consolidationprocess
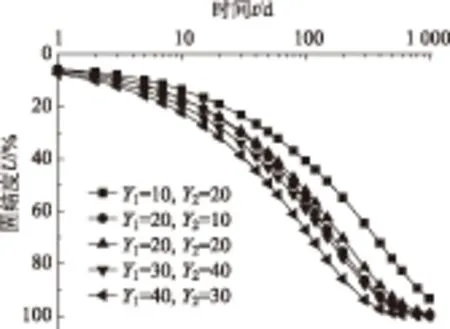
图6 桩土模量比对固结过程的影响Fig.6 Influence of pile-soil modulus ratio on consolidationprocess
图5、图6分别反映了桩径比n和桩土模量比Y1,Y2对固结过程的影响。由图5、图6可得,根据本文给出的计算模型,在复合地基设计参数取值范围内(通常n≤7),随着桩径比的减小,固结速率会增大;桩、土模量的增大和桩土模量比的增大会加快固结速率;其他条件相同时,双层不排水桩复合地基在双层土是上软下硬时固结更快,而当双层土是上硬下软时固结更慢。
图7给出了不同加荷历时下复合地基固结度随时间变化曲线。图中,加荷历时越短,表示加荷速率越大,tc=0代表瞬时加荷的情况。从图7中可以看出复合地基固结速率与加荷速率有关,复合地基的固结速率随加荷速率的增大而增大,而瞬时加荷情况下复合地基固结速率最大,这反映了本文考虑施工荷载为变荷载是有必要的。

图7 加荷速率对固结过程的影响 Fig.7 Influence of loading rate on consolidation process
图8、图9分别反映了渗透率之比和层高比对固结速率的影响。由图8、图9可得,kv2/kv1越大,固结越快;由图9可知,层高比越小,固结越快。总之,kv2/kv1越大,h2/h1越小,E2/E1越大,则双层不排水桩复合地基的固结速率越快。
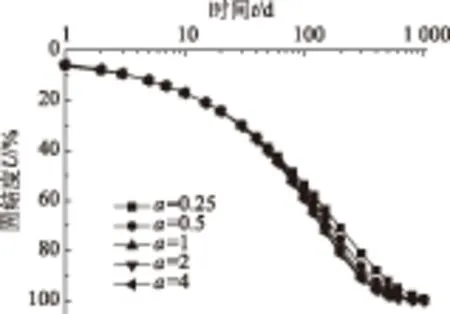
图8 上下土层渗透率之比对固结速率的影响Fig.8 Influence of ratio of soil layers’ permeability onconsolidation rate
图10对分别按平均孔压和按沉降定义得到的固结度曲线进行了比较。此图表明,对于所给计算参数,按两种不同定义分别得到的固结度会有差别,由式(25)可知,差别大小与各层土体的压缩模量有关,仅当各层土体的压缩模量相等时,按两种不同定义分别得到的固结度才会相等,而对于单层不排水桩复合地基,则不存在这种差别,图10从侧面反映了考虑地基土的成层性是有必要的。因此,在计算成层不排水桩复合地基的固结问题时,应对固结度的定义予以区别。

图9 层高比对固结速率的影响Fig.9 Influence of soil height ratio on consolidation rate

图10 分别按平均孔压和按沉降定义的固结曲线的比较Fig.10 Comparison of consolidation curves defined by average pore pressure and settlement respectively
4 结论
(1)本文的计算模型同时考虑了地基土的成层性和施工荷载随时间任意变化两个条件,不仅适用于变荷载下双层不排水桩复合地基的固结计算问题,而且在一定条件下可以方便地转化为单层不排水桩复合地基和双层天然地基的固结计算问题,因此具有普遍适用性。
(2) 参数分析结果表明:随着桩径比的减小和桩体刚度的增大,固结速率会增大;加荷速率越大,固结速率则越大,在瞬时加载情况下固结速率达到最大;kv2/kv1越大,E2/E1越大,h2/h1越小,则固结越快。
(3)分别按平均孔压定义和按沉降定义得到的双层不排水桩复合地基固结度会有一定程度的差别,差别大小与各层土体的压缩模量有关,仅当各层土体的压缩模量相等时,按两种不同定义分别得到的固结度才会相等。
参考文献:
[1] 侯永峰,龚晓南. 水泥土的渗透特性[J]. 浙江大学学报:工学版,2000,34(2): 77-81. HOU Yong-feng, GONG Xiao-nan. The Permeability of Cement-treated Soil[J]. Journal of Zhejiang University:Engineering Science Edition, 2000, 34(2): 77-81.
[2] 张玉国,海然,谢康和. 变荷载下散体材料桩复合地基固结研究[J]. 岩土工程学报,2009,31(6): 939-945. ZHANG Yu-guo, HAI Ran, XIE Kang-he. Consolidation of Composite Ground with Granular Columns under Time-dependent Loading[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 939-945.
[3] 卢萌盟. 复杂条件下复合地基固结解析理论研究[D]. 南京:浙江大学,2009. LU Meng-meng. Research on Analytic Theory of Consolidation of Composite Foundation under Complex Conditions[D]. Nanjing: Zhejiang University, 2009.
[4] 孙举,谢新宇,谢康和. 半透水边界双层复合地基固结解析理论[J]. 浙江大学学报:工学版,2007,41(9): 1467-1476. SUN Ju, XIE Xin-yu, XIE Kang-he. Analytical Theory for Consolidation of Double-layered Composite Ground under Impeded Boundaries[J]. Journal of Zhejiang University:Engineering Science, 2007, 41(9): 1467- 1476.
[5] 卢萌盟,谢康和,王玉林,等. 碎石桩复合地基非线性固结解析解[J]. 岩土力学,2010,31(6): 1833-1840. LU Meng-meng, XIE Kang-he, WANG Yu-lin, et al. Analytical Solution for Nonlinear Consolidation of Stone Column Reinforced Composite Ground[J]. Rock and Soil Mechanics, 2010, 31(6): 1833-1840.
[6] 杨涛,李国维. 路堤荷载下不排水端承桩复合地基固结分析[J]. 岩土工程学报,2007,29(12): 1831-1836. YANG Tao, LI Guo-wei. Consolidation Analysis of Composite Ground with Undrained Penetrating Piles under Embankment Load[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(12): 1831-1836.
[7] 杨涛,石磊,李国维. 变荷载下不排水端承桩复合地基固结分析[C]//第十届全国地基处理学术讨论会论文集.南京:东南大学出版社,2008: 206-209. YANG Tao, SHI Lei, LI Guo-wei. Consolidation Analysis of Composite Ground with Undrained Penetrating Piles under Time-dependent Load[C]//The 10th National Conference on Foundation Treatment. Nanjing: Southeast University Press, 2008: 206-209.
[8] 杨涛,石磊,李国维. 路堤分级填筑条件下不排水端承桩复合地基固结分析[J]. 公路交通科技,2008,25(10): 31-35. YANG Tao, SHI Lei, LI Guo-wei. Consolidation Analysis of Composite Ground with Undrained Penetrating Piles under Stage Embankment Construction[J]. Journal of Highway and Transportation Research and Development, 2008, 25(10): 31-35.
[9] 卢萌盟,谢康和,周国庆,等. 不排水桩复合地基固结解析解[J]. 岩土工程学报,2011,33(4): 574-579. LU Meng-meng, XIE Kang-he, ZHOU Guo-qing, et al. Analytical Solution for Consolidation of Composite Ground with Impervious Pile [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(4): 574-579.
[10]YANG T, YANG J Z, NI J. Analytical Solution for the Consolidation of a Composite Ground Reinforced by Partially Penetrated Impervious Columns[J]. Computers and Geotechnics, 2014, 57(2): 30-36.
[11]GONG X N, TIAN X J, HU W T. Simplified Method for Predicating Consolidation Settlement of Soft Ground Improved by Floating Soil-cement Column[J]. Journal of Central South University, 2015, 22(7): 2699-2706.
[12]谢康和. 双层地基一维固结理论与应用[J]. 岩土工程学报,1994,16(5): 24-35. XIE Kang-he. Theory of One-dimensional Consolidation of Double-layered Ground and Its Application [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24-35.
[13]TANG X W, ONITSUKA K. Consolidation of Double-layered Ground with Vertical Drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(14): 449-1465.
[14]王瑞春,谢康和,唐晓武. 未打穿散体材料桩复合地基固结解析研究[J]. 公路交通科技,2004,21(4): 12-16. WANG Rui-chun, XIE Kang-he, TANG Xiao-wu. Analytical Study on Consolidation of Composite Ground with Partially Penetrated Granular Columns[J]. Journal of Highway and Transportation Research and Development, 2004, 21(4): 12-16.
[15]王瑞春. 竖井地基和散体材料桩复合地基固结解析研究[D]. 杭州:浙江大学,2001: 88-118. WANG Rui-chun. Analytical Studies on Consolidation of Soft Clay Ground Improved by Vertical Drains or Granular Columns[D]. Hangzhou:Zhejiang University, 2001: 88-118.
[16]GB/T 50279—2014,岩土工程基本术语标准[S]. GB/T 50279—2014, Standard for Fundamental Terms of Geotechnical Engineering[S].
Analysis of 1D Consolidation of Double-layered Composite Foundation with Impervious Pile under Time-dependent Loading
ZHAO Ming-hua,WU Yue-wu,ZHENG Yue
(School of Civil Engineering, Hunan University, Changsha Hunan 410082, China)
Assuming that the weak drainage piles are undrained in composite foundation, considering both layered soils and time-dependent loading, we derived the 1D consolidation control equations of double-layered composite foundation with impervious pile under time-dependent loading, and obtained the general analytical solutions of the excess pore water pressure of such foundation. Then, we gave the analytical solutions of the excess pore water pressure and the consolidation degree in the common cases of instantaneous loading and single-stage constant loading respectively. After that, we verified the reasonableness of the analytical solution through the ways of numerical example and the degradation of the solutions in this article to classical solutions. Finally, we investigated the consolidation rule of double-layered composite foundation with impervious pile by programming computation. The result shows that (1) the consolidation rate will increase when the pile stiffness increases and loading rate increases while the pile diameter ratio decreases; (2) whenkv2/kv1is greater,h2/h1is smaller andE2/E1is greater, the consolidation rate is greater; (3) the consolidation degrees are different when defined by average excess pore water pressure and settlement respectively, and the size of difference is related to the soil’s compression modulus of each layer.
road engineering; composite foundation;impervious pile;consolidation;double-layer;time-dependent loading
2016-06-12
国家自然科学基金项目(51478178)
赵明华(1956- ),男,湖南洞口人,教授,博士生导师.(mhzhaohd@21cn.com)
10.3969/j.issn.1002-0268.2016.11.007
TU
A
1002-0268(2016)11-0042-08

