时域差分滤波在高速铁路轨道精密检测中的应用

马文静 刘召才

(中铁工程设计咨询集团有限公司，北京 100055)



时域差分滤波在高速铁路轨道精密检测中的应用

马文静 刘召才

(中铁工程设计咨询集团有限公司，北京 100055)

高速铁路轨道精密检测直接服务于轨道精调作业，检测数据的好坏对轨道精调有着重大影响。检测数据在反映轨道真实状态的同时，还存在由误差引起的高频扰动，而这种高频扰动对精调数据分析极为不利。结合轨道精密检测的实践，采用时域差分技术消除数据高频扰动，并通过某高速铁路实测数据对算法进行验证，计算结果表明，数据中的高频分量得到有效消除。

高速铁路 时域差分 轨道检测 轨道精调

1 概述

为满足列车高速平稳运行，要求建成的轨道具有高平顺性。板式无砟轨道在轨道板施工时有调板的环节，双块式无砟轨道也存在轨排精调的过程，其目的都是为了保证承轨台的位置准确，从而使后期铺设的长钢轨尽可能地与设计位置保持一致。由于施工误差、测量误差等各种复杂因素的影响，在长钢轨铺设完成并经过应力放散、锁定后，仍然需要进行长轨精调，以保证轨道最终的平顺性。

长轨精调的前提是轨检小车对轨道的静态精密检测，通过对左右轨平面偏差、左右轨高程偏差、轨距偏差、超高偏差、扭曲偏差等轨道检测数据的分析，得到轨道每一个扣件处的平面及高程调整量，从而指导轨道调整并使轨道平顺性满足规范[1-2]要求。轨道静态精密检测的作业流程如图1所示，智能型全站仪基于轨道控制网(CPⅢ)进行自由设站并对轨检小车进行定位，再结合轨距、超高等传感器的数据，解算出轨检小车当前位置处的轨道几何状态参数，通过逐轨枕的数据采集，完成对轨道的精密检测。

图1 轨检小车作业示意

为了保证检测数据的高精度，对测量设备及检测作业流程有着严格的控制[3]，在数据处理方面，对全站仪自由设站精度、设站距离、搭接测量精度等方面也有着较多的方法[4-9]。测量过程中，由于环境、测量仪器等因素的综合影响，测量数据中仍然不可避免地存在扰动，这种数据扰动不同于测量粗差，其量级通常很小，约在0.5 mm以下。在数据分析过程中，如果不考虑这种微小扰动，会对轨道平顺性分析结果产生一些不利影响，并可能加大轨道调整量及成本支出。基于此，可利用时域差分滤波的处理方法来消除数据微小扰动，达到优化数据分析的目的。

2 时域差分滤波原理

通常利用高阶线性常系数差分方程来描述一个时域差分滤波系统，其数学表达式为[10]

式中，y[n]为输出序列，x[n]为输入序列，n为时刻，式(1)表明利用差分方程进行数据处理后，n时刻的输出不仅跟从n开始向前一系列时刻的输入有关，同时还跟向前一系列时刻的输出有关，其揭示的逻辑关系表明任一时刻的输出都不是孤立的。利用z变换得到式(1)的系统函数为

式(2)表明，通过系数ak及bk对系统输出y[n]的幅度特性、频率特性及相位特性均进行了调整，选择合适的阶数(M及N)、ak及bk，能够有效滤除数据序列中特定的频率成分及幅度，从而得到期望的数据处理结果。对式(1)进行改化得到如式(3)所示的实用数据处理递推公式

对式(3)的计算流程进行分解，得到该式的框图(如图2所示)。由图2可知，差分方程的实质为对输入序列x[n]及输出序列y[n]进行一系列延时操作，然后再进行线性组合得到输出结果。这种数据处理过程为对式(3)进行傅里叶分析带来了方便，通过简单的傅里叶变换，可以在频域更加细致地分析经过差分系统处理后的数据在频率及幅度上的变化，从而得到差分系统的性能。

图2 线性常系数差分方程的方框图

3 轨道检测数据的高频滤波

前已述及，在轨道检测数据中含有高频扰动成分，如不消除，将对最终的轨道平顺性分析造成不利影响。由于检测数据反映的是轨道的真实状态，而建成轨道相邻扣件间的几何状态具有高度的相关性，利用时域差分原理可以很好地解决数据的高频扰动问题。

选用一阶差分方程来进行轨道检测数据的高频滤波

式(4)表明n时刻的输出不仅跟n时刻的输入有关，还跟n-1时刻的输出有关。在轨道检测中，时刻的前后对应空间的位置，因此式(4)也表明当前扣件处的轨道几何状态信息不仅跟当前的测量值有关，同时也跟前一扣件处的轨道几何状态信息有关，从而从数学形态上描述了轨道相邻扣件间的相关性，这种相关性的强弱通过系数a及b来调整。

对式(4)进行傅里叶变换，得到输入与输出之间的傅里叶变换关系

式(5)中，Y(ejw)为y[n]的傅里叶变换，X(ejw)为x[n]的傅里叶变换，H(ejw)为系统函数，其作用为对X(ejw)的选频部分进行增强或抑制，从而达到滤波的目的。a及b的不同组合代表了系统函数不同的选频特性，其取值范围为[0，1]，同时还应满足

ejw是模为1的周期复函数，因此可在[-π，π]的范围内研究系统函数的特性。在采用不同系数组合的情况下，对系统函数H(ejw)的实部、虚部、模及相位作图(如图3所示)。

图3 一阶差分系统的频率响应

由图3中“模”图可知，式(4)描述的差分系统对输入序列的高频部分有很强的抑制作用，而对低频部分则予以通过；且对输入序列的的幅度只减弱，不增强。a值越大，b值越小时，系统的高频滤波性能就越强，也表示上一时刻输出对当前时刻输出的影响越大。

在轨道检测数据处理的实际应用中，a值并不是取得越大越好，a值越大，表明当前扣件处的轨道几何状态信息更多地受到前一扣件的影响，而这与轨道检测获取每一扣件处实际几何状态信息的本意不符。因此，应用一阶差分系统滤波，应该在当前测量信息与前一输出信息之间取得一种平衡，使得最终输出结果既能很好地反映轨道的实际状态，同时也能很好地滤除数据中的高频扰动。这种平衡的取得，其实现方法在于如何选取a及b的数值。合适的数值选取，也使得数据处理的思维方法得到了具体的数学实现。

4 算例分析

为验证该滤波算法，选取某客运专线右线的实际轨道检测高程数据进行分析。该段轨道检测数据位于DK30+900～DK31+970，处于半径为6 995 m的圆曲线上，设计超高170 mm，总长约1 070 m，共计测点1 710个。滤波前及应用式(4)滤波后的轨道高程检测数据的波形如图4及图5所示。

图4 一阶差分滤波前轨道高程偏差波形

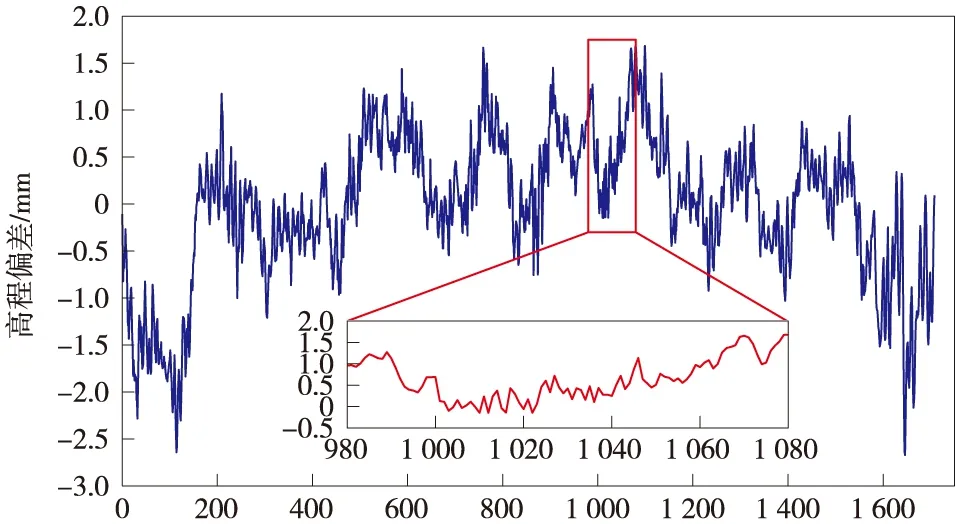
图5 一阶差分滤波后轨道高程偏差波形

由图4及图5的比较可知：经过差分滤波后的数据波形，虽然在整体的形状上与滤波前保持一致，但是数据的波动剧烈程度得到了明显的降低，从第980到1 080这100个点的细化波形上能更直观地看出这一点，滤波前的数据呈现出一种起伏较大的锯齿状，滤波后数据的锯齿状程度显著好转。上述结果表明，一阶差分滤波系统较好地达到了预期的设计目的，降低了轨道检测数据在微观尺度上的波动程度，并在不影响数据真实可靠的前提下，使数据更加平滑。

对滤波前及滤波后的轨道检测数据进行离散时间傅里叶变换，得到数据在频域的波形(如图6所示)。

应用快速傅里叶变换FFT算法[11-12]，可以很方便地获得y[n]的傅里叶变换Y(ejw)，为作图方便，对Y(ejw)的模值按下式取为对数幅度

图6 滤波前后检测数据的傅里叶变换对数幅度比较

图6中，虚线为滤波前轨道高程偏差的FFT数据，实线为滤波后轨道高程偏差的FFT数据。在[0，π]的作图范围内可见，低频范围内滤波前后的傅里叶变换对数幅度基本相同，在[1，π]的范围内，滤波后对数幅度较滤波前的对数幅度整体偏小，并随着频率的增大，幅度差值也逐渐增大。在[2.5，π]频率段的细化图中可以更清晰地看到，滤波后的对数幅度较滤波前整体偏小约10左右。由上述分析可知，式(4)表示的一阶线性差分滤波系统对数据的高频部分进行了很好的抑制，对数据的低频部分则给予保留，从而在保持数据真实性的基础上，使数据得到较好的平滑，达到了滤波系统预期的设计目的。

5 结束语

采用一阶线性差分系统进行数据滤波处理，并利用傅里叶变换从理论上证明了该方法的有效性，同时利用一段实际的轨道检测数据，分析比较滤波与不滤波两种情况下的数据异同，进一步表明了滤波系统所能达到的数据处理效果。应用本文方法，能较好地处理轨道静态精密检测中数据跳动幅度小于0.5 mm的高频扰动，使数据更加真实反映轨道的实际几何状态，为获得更优的轨道平顺性分析及调整量输出奠定了数据基础。

[1] 铁道部.TB10601—2009高速铁路工程测量规范[S].北京：中国铁道出版社，2009

[2] 铁建设函[2009]674号高速铁路无砟轨道工程施工精调作业指南[S]

[3] 科技基[2008]86号客运专线轨道几何状态测量仪暂行技术条件[S]

[4] 王洪斌，任海锋，张冀辉.全站仪自由设站边角交会网在铁路精密控制测量中的应用[J].测绘与空间地理信息，2013(12)：221-223

[5] 何荣，崔灿.基于间接平差的自由设站点与监测点联合平差研究[J].河南理工大学学报：自然科学版，2013(3)：298-301

[6] 杨雪峰，刘成龙，刘胜.高铁轨道精测站间搭接精度指标合理性研究[J].铁道科学与工程学报，2014(6)：132-136

[7] 李阳腾龙，岑敏仪，杨晓云.高速铁路轨道检测点的数据处理[J].测绘通报，2014(8)：65-67

[8] 罗文彬.客运专线轨道精调相邻站平顺衔接方法研究[J].铁道标准设计，2014(8)：23-26

[9] 全志强. 高速铁路轨道位置测量误差的分析[J].测绘通报，2015(3)：74-75

[10]A.V.奥本海姆，R.W.谢弗，J.R.巴克.离散时间信号处理[M].刘树棠，黄建国，译.西安：西安交通大学出版社，2011

[11]维纳.K.英格尔，约翰.G.普罗克斯.数字信号处理(MATLAB版)[M].刘树棠，译.西安：西安交通大学出版社，2011

[12]万永革.数字信号处理的MATLAB实现[M].北京：科学出版社，2012

Application of Difference Filter Time Domain in High Speed Railway Track Detection

MA Wenjing LIU Zhaocai

2016-09-20

马文静(1981—)，男，2007年毕业于西南交通大学大地测量学与测绘工程专业，硕士，高级工程师。

1672-7479(2016)06-0001-03

U212.24

B