N空位、Ga空位对GaN∶Mn体系电磁性质和光学性质影响的第一性原理研究＊

蒋联娇，符斯列，秦盈星，李健翔

(华南师范大学 物理与电信工程学院，广东省量子调控工程与材料重点实验室，广州 510006)

N空位、Ga空位对GaN∶Mn体系电磁性质和光学性质影响的第一性原理研究＊

蒋联娇，符斯列，秦盈星，李健翔

(华南师范大学 物理与电信工程学院，广东省量子调控工程与材料重点实验室，广州 510006)

基于密度泛函理论的第一性原理平面波超软赝势法分别计算了VGa和VN距掺入Mn原子为近邻、次近邻、远近邻各3种情况下GaN体系的电子结构和光学性质，分析比较了空位的不同位置对Mn掺杂GaN体系磁性的影响。计算结果表明，Mn掺杂会导致GaN体系带隙增大且体系表现为半金属铁磁性；VN的存在会增强缺陷复合物体系的铁磁性，且随着VN相对杂质Mn距离越近，体系总磁矩增加；而VGa的存在会降低缺陷复合物体系的铁磁性，且随Ga空位相对杂质Mn距离越近，体系总磁矩减少。不同位置的VGa和VN均会导致缺陷复合物体系主吸收峰和光吸收边相对于单Mn掺杂而言向低能方向移动，出现红移现象。

GaN晶体；Mn掺杂；空位；电子结构；光学性质

0 引 言

稀磁半导体(diluted magnetic semiconductor, DMS)是指由磁性过渡族金属元素或稀土金属元素部分取代Ⅱ-Ⅳ族或Ⅲ-Ⅴ族化半导体中非磁性阳离子后所形成的一类新型半导体合金材料。这种材料可以同时实现对电子电荷和自旋两种自由度的应用，是一种优质的自旋极化载流子源，如自旋注入或者自旋极化输运等[1]，已成为当前国际上磁电子学领域的研究热点。

氮化镓(GaN)作为第三代半导体材料的代表，具有优良的光电特性、宽的直接带隙(Eg=3.39 eV)和稳定的物理特性，广泛的应用于蓝、绿发光二极管、蓝光激光器、紫外波段的探测器以及高温、大功率集成电路，是当今世界上最为先进的半导体材料之一。目前大量研究表明在过渡族元素中，Mn掺杂GaN的效应最为明显，可实现高于室温的居里温度(TC)[2-5]，而高的TC以充分保证相关器件的热稳定性和广泛的应用范围。邢海英等[6-8]采用第一性原理计算不同Mn浓度掺杂GaN证实了材料表现为半金属特性，是实现自旋注入的理想材料。Katayama-Yoshidia等[9]采用密度泛函理论研究了Mn掺杂GaN，发现Ga1-xMnxN(x=0.25)具有稳定的铁磁基态。毋志民等[10]研究了不同浓度下Mn掺杂GaN稀磁半导体的电磁特性，表明随着Mn掺杂浓度的增加，体系的半金属性有所增强。介伟伟、杨春等[11]基于密度泛函理论(DFT)讨论了Ga和N不同比例下各种空位缺陷对GaN性能的影响，发现N空位的增加会导致GaN电导率下降；在实验方面，目前已采用化学气相沉积(CVD)[12]、金属有机物化学气相沉积(MOCVD)[13]、氢化物气相外延(HVPE)[14]等方法制备各种GaN材料，但由于生长工艺条件的限制，难以制备出完美的GaN单晶和薄膜，本征缺陷(如Ga空位、N空位等)和非故意掺杂会不可避免的产生，使生长出的GaN除了带间跃迁外，还存在黄色发光带。Sedhain等[15]通过观察GaN在红外区域的发射光谱确定Ga空位(VGa)和最近邻的氮位的氧(ON)形成的复合体是黄光的来源。徐大庆等[16]利用拉曼散射和光致发光谱研究了Mn离子注入Mg掺杂GaN的微结构和光学特性，发现在低能区出现新的发光峰来源于MgGa-VN复合体深施主能级及Mg、Mn相关的受主能级之间的辐射复合跃迁。虽然目前的研究结果大大促进了Mn掺杂GaN的发展，但是关于本征点缺陷对掺杂体系影响的研究尚显不足。

为详细了解不同的空位缺陷的出现对Mn掺杂GaN体系的影响，本文基于密度泛函理论的第一性原理平面波超软赝势法，分析讨论了含VN和VGa的缺陷复合物体系中缺陷存在的位置相对Mn杂质的不同而引起相应的体系的电磁性质和光学性质的变化，以期为实验研究提供有意义的理论参考。

1 模型构建和计算方法

1.1 模型构建

理想的GaN多为六方纤锌矿结构[17]，属于P63mc空间群，对称性为C6v-4，晶格参数为a=b=0.3189 nm，c=0.5185 nm，其中c/a为1.626，比理想的六角密堆积结构的1.633小，c方向的键长为0.1969 nm，其它方向的键长为0.1965 nm，其晶胞由Ga的六角密堆积和N的六角密堆反向套构而成。文中计算结构均基于超晶胞模型，取2×2×2(32个原子)超晶胞体系，每个超晶胞包含16个Ga原子和16个N原子。掺杂时每个超胞由一个Mn原子替代一个Ga原子实现掺杂，因为理论计算和实验表明Mn替代Ga的晶格位置最为稳定的[18-19]，掺杂浓度为6.25%(如图1(a))。计算空位时去除超晶胞内部的一个Ga原子形成VGa，或者去除一个N原子形成VN。在分析Ga空位和N空位对Mn掺杂GaN体系的影响时以相对于该掺杂Mn原子的距离远近分别对比了近邻、次近邻和远近邻空位各3种情况，即GaN∶Mn-VGa1(近邻Ga空位)、GaN∶Mn-VGa2(次近邻Ga空位)、GaN∶Mn-VGa3(远近邻Ga空位)、GaN∶Mn-VN1(近邻N空位)、GaN∶Mn-VN2(次近邻N空位)、GaN∶Mn-VN3(远近邻N空位)6种类型。其超胞模型分别如图1所示。

图1 32个原子体系超晶胞结构图

1.2 计算方法

本文利用Accelrys公司的Materials Studio软件建立模型，并采用软件中的Castep(cambridge serial total energy package)程序[20]计算。Castep是一个基于密度泛函理论(DFT)结合平面波赝势方法的从头算量子力学计算程序。计算中采用周期性边界条件，利用广义梯度近似(generalized gradient approximation, GGA)的PBE处理电子间的交换关联能，电子波函数通过平面波基矢组扩展，并采用超软赝势[21]描述离子实与价电子间的相互作用，以尽量减少平面波基矢的个数。选取的Ga、N、Mn各原子的价电子组态分别为Ga：3d104s24p1、N：2s22p3，Mn：3d54s2(Mn自旋态设为up)，其它轨道电子视为芯电子。不对称布里渊区取样采用4×4×2的Monkhorst-Pack格子[12]；在自洽场运算中，采用Pulay密度混合法。晶格结构和原子坐标采用BFGS(Broyden-Fletcher-Goldfarb-Shanno)方法[23]进行毫无约束的完全弛豫。在几何优化的过程中，优化参数有4个，即单原子能量、原子间相互作用力，晶体内应力和原子最大位移。它们的收敛标准分别被设置为5×10-6eV/atom，0.1 eV/nm，0.02 GPa和0.00005 nm。计算程序对4个参数同时进行优化，结构优化完成的标志是4个参数均达到或者优于收敛标准，然后采用优化好的超胞进行能量计算。

2 计算结果与讨论

2.1 纯GaN及含点缺陷GaN体系的能带结构

本文首先对纯GaN超胞进行结构优化，所得晶格结构参数与实验值的比较如表1所示。

表1 优化后GaN晶格参数与实验值[24]比较

Table 1 The comparision between the optimized GaN lattice parameters and the experimental value[24]

晶体结构参数实验值/nm计算值/nma0.31890.3223c0.51850.5249c/a1.6261.629

由表1的数据可以看出，优化后c/a=1.629与实验值1.626符合的很好，偏差仅为0.18%，与文献[6-7]计算的结果相近，说明本文计算方法的可靠性。

理想的纤锌矿GaN的能带结构如图2(a)所示，可以看出价带顶和导带底均位于Brillouin的G点处，是直接带隙半导体，计算所得禁带宽度为1.70 eV，略低于文献[6]的计算结果1.98 eV，但是均小于实验值3.39 eV。这是由于在计算中采用DFT是基态理论，而能隙属于激发态，得到的结果偏低是采用该理论时普遍存在的现象[25]，但这并不影响对GaN及其相关体系的定性分析。

图2 GaN能带结构、GaN-VN能带结构和GaN-VGa能带结构

由图2(b)、(c)和(d)可以看出，VN会使GaN变为间接带隙半导体，并且VN和VGa的存在会使得GaN的禁带宽度分别增加至1.80和2.00 eV。此外，VN在导带底位置引入了施主能级，是一种施主缺陷。VGa导致费米能级向低能级方向移动进入价带，从而在价带顶位置形成一部分占据能级，价带内的电子可以跃迁到此能级上而产生空穴，因此VGa为受主缺陷，这与文献[11]得出的结果相符。

2.2 N空位、Ga空位对Mn掺杂GaN体系的电子结构

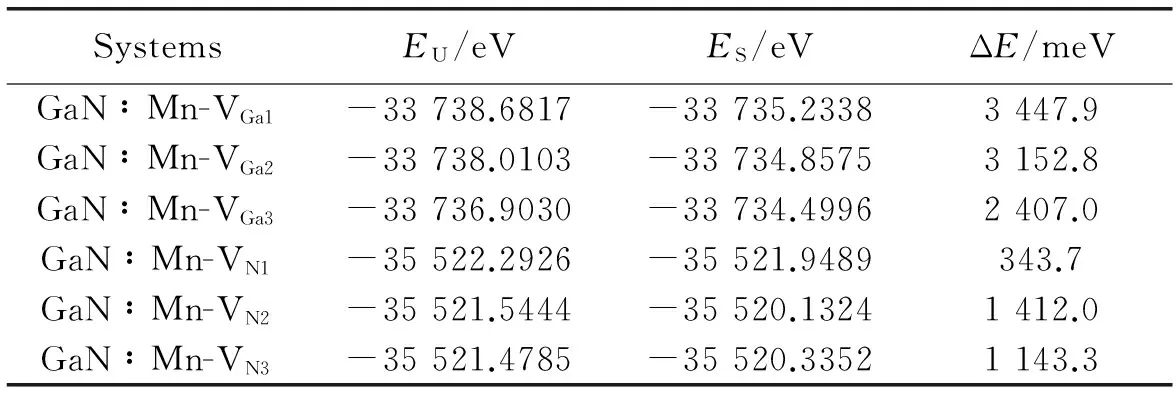
对近邻、次近邻、远近邻N空位和Ga空位与Mn掺杂共存的6种类型GaN体系进行自旋极化计算与非自旋极化计算，结果显示(见表2)自旋极化的总能比非自旋极化的总能低，说明这6种体系均倾向于自发的自旋极化。

表2 非自旋极化能量EU与自旋极化能量ES比较及其能量差ΔE(EU-ES)

Table 2 The comparision of non-spin polarization energyEUand spin polarization energyESand the energy difference ΔE(EU-ES)

SystemsEU/eVES/eVΔE/meVGaN∶Mn-VGa1-33738.6817-33735.23383447.9GaN∶Mn-VGa2-33738.0103-33734.85753152.8GaN∶Mn-VGa3-33736.9030-33734.49962407.0GaN∶Mn-VN1-35522.2926-35521.9489343.7GaN∶Mn-VN2-35521.5444-35520.13241412.0GaN∶Mn-VN3-35521.4785-35520.33521143.3

图3为各个体系的能带结构图。(a)、(b)为单Mn掺杂GaN的能带图，可以看出单个Mn原子掺入后的GaN体系仍为直接带隙半导体，其导带底与价带顶仍位于布里渊区的G点，带隙值Eg=2.13 eV，较未掺杂时的1.70 eV有所增大，因加入了合金成分Mn所致。杂质Mn的掺入最显著的特征是能带图出现了与Mn有关的自旋极化杂质带，位于价带顶上方EV+1.12 eV处，为深受主能级，该结果与理论[26-27]和实验[28]基本相符。图3(a)中t2d和ed分别代表Mn离子的3d能级在四面体晶体场中分裂成三度简并的t2轨道与两度简并的e轨道，无掺杂时GaN体系自旋向上和自旋向下的能带相同，未产生能带自旋劈裂，故没有磁性。掺入Mn后，体系上下自旋产生劈裂，自旋向上能级占据费米面，自旋向下能级未占据费米面，即在杂质带中产生100%的自旋极化输运，且EF贯穿杂质带中，表明掺杂体系具有一定的半金属铁磁性，这与文献[6，29]得出的结果相符。图3(c1,2,3)、(d1,2,3)依次为含近邻、次近邻和远近邻VN的缺陷复合物体系的能带图，图(e1,2,3)、(f1,2,3)依次为含近邻、次近邻和远近邻VGa的掺杂体系能带结构图，可以看出VN的存在在导带底附近引入了施主杂质能级，且费米能级向高能导带方向移动。VGa的存在在价带顶引入受主能级，且费米能级向低能价带方向移动。但是不论VN还是VGa的各个缺陷复合物体系中的自旋向上与自旋向下的能带图中的费米能级上方均出现了空的杂质带，故各个体系中费米能级上方空穴载流子的个数相比于单Mn掺杂而言有所增加，导致相应的价带越向高能级方向移动，从而导致相应的带隙变窄且各体系的电导率增加。含VN各缺陷复合物体系的带隙由原来的2.13 eV依次减少到1.49，1.47和1.54 eV。含VGa各缺陷复合物体系的带隙由原来的2.13 eV依次减少到2.10，1.61，1.71 eV。

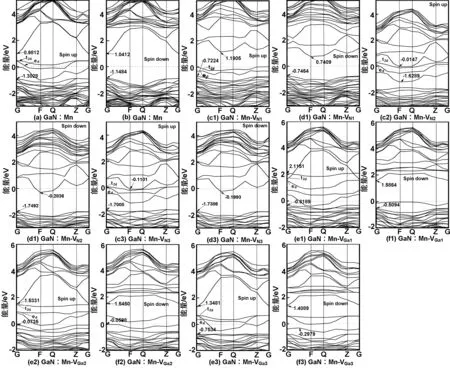
图3 GaN∶Mn、GaN∶Mn-VN1、GaN∶Mn-VN2、GaN∶Mn-VN3、GaN∶Mn-VGa1、GaN∶Mn-VGa2和GaN∶Mn-VGa3能带结构

Fig 3 Energy band structures of GaN∶Mn，GaN∶Mn-VN1，GaN∶Mn-VN2，GaN∶Mn-VN3，GaN∶Mn-VGa1，GaN∶Mn-VGa2and GaN∶Mn-VGa3

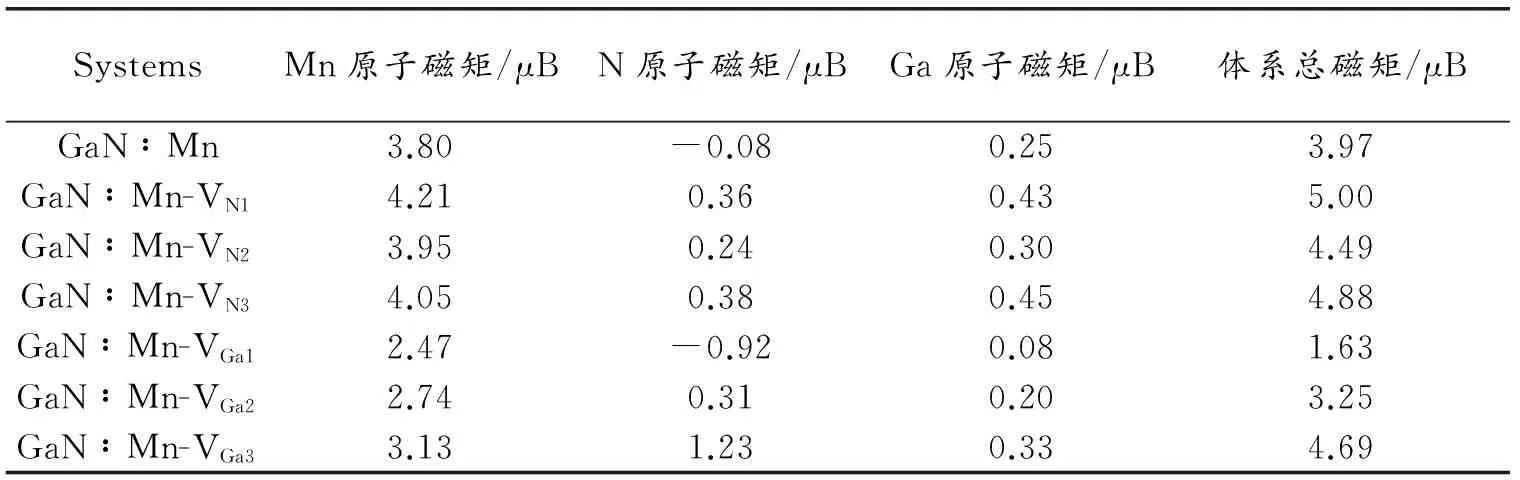
图4为各体系的分波态密度图。可以看出相对于单Mn掺杂而言，VN的引入均使得费米能级向高能导带方向移动，带隙变窄，这与上文所得的结果相符。在费米能级附近，含VN的缺陷复合物体系中Mn3d与N2p态各个峰态局域化明显，且Mn3d与N2p态自旋劈裂的强度明显增加，费米能级附近相应的态密度峰值均比单Mn掺杂体系要大，表明VN的存在增强了Mn3d与N2p态之间的杂化，进而增强了缺陷复合物体系的半金属铁磁性。且随着VN距离杂质Mn越近，p-d之间的杂化作用越强，体系的半金属铁磁性越强。表3的数据进一步说明了VN的存在增强了缺陷复合物体系的铁磁性，VN相对杂质Mn距离越近，p-d交换相互作用越强，缺陷复合物体系的总磁矩越大。其中近邻VN对缺陷复合物体系的总磁矩提升最为显著，由原来的3.97 μB增加到5.0 μB。

图5为各体系的分波态密度图。由图5可以看出，相对于单Mn掺杂而言，VGa的引入均使得费米能级向低能价带方向移动，带隙变窄，这与上文所得的结果相符。在费米能级附近N2p态发生了显著的变化，其费米能级由原本仅通过自旋向上通道，但却处于自旋向下的带隙内变为即通过自旋向下通道又通过了自旋向上通道。导致费米能级附近上、下自旋通道的不对称性明显地缩小，其自旋劈裂的程度大为减弱。且在费米能级附近Mn3d态的各个峰态变得弥散化，非局域化加强，其相应态密度峰值也有所减少，故表明VGa的存在减弱了Mn3d与N2p之间的杂化，进而减弱了缺陷复合物体系的半金属铁磁性，且随着VGa距离杂质Mn越近，p-d之间的杂化作用越弱，体系的半金属铁磁性越弱。表3数据进一步证实VGa的存在会基本上会降低缺陷复合物体系的铁磁性，且随VGa相对杂质Mn距离越近，体系总磁矩越少。其中近邻VGa对缺陷复合物体系的磁矩降低最为显著，由原来的3.97 μB降低到1.63 μB。

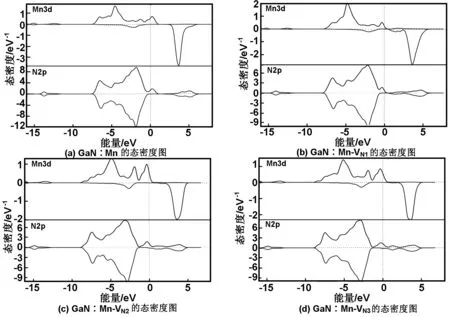
图4 GaN∶Mn、GaN∶Mn-VN1、GaN∶Mn-VN2和GaN∶Mn-VN3的态密度图

图5 GaN∶Mn、GaN∶Mn-VGa1、GaN∶Mn-VGa2和GaN∶Mn-VGa3的态密度图

2.3 光学性质

光学性质是沟通带间跃迁微观物理过程与固体电子结构的桥梁，反映了固体能带结构及其各种光谱信息。本文计算了掺杂体系的介电函数和吸收光谱，并予以分析。在线性响度的范围内半导体的宏观光学性质能够用复介电函数来描述

ε(ω)= ε1(ω)+ iε2(ω)

其中

ε1=n2- k2，ε2=2nk

根据直接跃迁概率定义和Kramers-Kronig色散关系可以推出晶体介电函数的实部ε1(ω)、虚部ε2(ω)和晶体的光吸收系数α(ω)[30-31]分别为

(1)

(2)

(3)

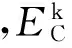
表3 GaN∶Mn及6种缺陷GaN体系的各原子磁矩大小及总磁矩大小比较

Table 3 The comparison between Mn doping GaN and six kinds of defects in Mn doping GaN systems of atomic magnetic moment and total magnetic moment

SystemsMn原子磁矩/μBN原子磁矩/μBGa原子磁矩/μB体系总磁矩/μBGaN∶Mn3.80-0.080.253.97GaN∶Mn-VN14.210.360.435.00GaN∶Mn-VN23.950.240.304.49GaN∶Mn-VN34.050.380.454.88GaN∶Mn-VGa12.47-0.920.081.63GaN∶Mn-VGa22.740.310.203.25GaN∶Mn-VGa33.131.230.334.69

图6为各个体系光吸收谱图和光吸收谱图，分析时采用的极化方向为(100)。由吸收谱图可观察到GaN∶Mn在1.04 eV左右出现小的吸收峰，主要是源于Mn离子杂质子带的带内跃迁，有关理论计算[32]证明Mn4+离子4T1(F)态与4T2(F)态间的跃迁能为1.0 eV，故该吸收峰是源于Mn4+离子基态4T1(F)态与4T2(F)态间的跃迁，这与文献[7]观察到的结果相近。而近邻VN会导致该吸收峰消失，这是因为近邻VN的存在会产生施主补偿效应，使得价带中的电子浓度增加，引起EF向导带移动从而导致该吸收峰消失。

图6 GaN掺杂体系的吸收光谱和GaN掺杂体系的介电函数虚部

此外，含VN的缺陷复合物体系的主吸收峰和光吸收边相对于单Mn掺杂而言向低能方向移动，出现红移现象，其原因在于VN的存在造成该体系的带隙变窄；且其主峰峰值强度随N空位距离Mn的位置越近，下降越明显，这是由于VN距离杂质Mn愈近引起缺陷复合物体系晶格弛豫的时间愈长[33]。而含VGa的缺陷复合物体系的主吸收峰和光吸收边的变化与含N空位的情况相似，但主峰峰值强度随VGa距离Mn的位置越近，下降的越少，与含VN的情况不同的是VGa距离杂质Mn愈近反而造成该体系的晶格弛豫的时间愈少[33]。

由介电函数的虚部图可观察到GaN∶Mn在低能区出现介电峰，对含VN的缺陷复合物体系而言，近邻VN的存在会导致该体系在低能区的介电峰消失，这点与吸收光谱的情况相符。而次近邻VN的存在引起该体系在低能区的介电峰的峰值强度大增，这是由于次近邻的VN使得该体系的费米能级移向导带底引起禁带中Mn的3d轨道电子到导带底的跃迁几率大增；相对于含VGa的缺陷复合物体系而言，含近邻和次近邻VGa的缺陷复合物体系的在低能区介电峰峰值相对于单Mn掺杂而言有所降低，而含远近邻的VGa的缺陷复合物体系的介电峰峰值强度却大增，这是在于远近邻VGa使得该体系的费米能级移向价带顶，大大促使了该体系中Mn的3d轨道电子和N的2p轨道电子向导带底的跃迁。

3 结 论

采用基于密度泛函理论的第一性原理平面波超软赝势法计算了VN和VGa对Mn掺杂GaN体系的电学和光学性质的影响。计算结果表明，VN空位和VGa的存在均使GaN体系的带隙增大，其中VN是一种施主缺陷，而VGa是一种受主缺陷。单Mn掺杂会使得GaN体系的带隙增加，且体系表现出半金属铁磁性，该结果与现有的理论和实验相符。VN的存在会增强Mn掺杂GaN体系的铁磁性，近邻VN对缺陷复合物体系的铁磁性增强作用最为明显，该体系磁矩最大；而VGa的存在会降低Mn掺杂GaN体系的铁磁性，近邻VGa空的存在使得缺陷复合物体系的总磁矩大为减少。此外，VGa和VN的存在均会导致缺陷复合物体系的主吸收峰和光吸收边相对于单Mn掺杂而言向低能方向移动，出现红移现象。而在介电函数图中只有近邻N空位导致掺杂体系的在低能区的介电峰消失。

[1] Youn C J, Jeong T S, Han M S, et al. Influence of various activation temperatures on the optical degradation of Mg doped InGaN/GaN MQW blue LEDs[J]. Journal of Crystal Growth, 2003, 250(3):331-338.

[2] Crooker S A, Furis M, Lou X, et al. Imaging spin transport in lateral ferromagnet/semiconductor structures[J]. Science, 2010, 309(5744):2191-2195.

[3] Schilfgaarde M V, Mryasov O N. Anomalous exchange interactions in Ⅲ-Ⅴ dilute magnetic semiconductors[J]. Physical Review B, 2001, 63(23):233205.

[4] Jungwirth T, König J, Sinova J, et al. Curie temperature trends in (Ⅲ,Mn)Ⅴ ferromagnetic semiconductors[J]. Physical Review B, 2002, 66(1):81-88.

[5] Sato K, Bergqvist L, Kudrnovsky J, et al. First-principles theory of dilute magnetic semiconductors[J]. Reviews of Modern Physics, 2010, 82(2):1633-1690.

[6] Xing Haiying, Fan Guanghan, Zhao Degang, et al. Electronic structure and optical properties of GaN with Mn-doping[J]. Acta Physica Sinica, 2008, 57(10):6513-6519.

邢海英，范广涵，赵德刚，等. Mn掺杂GaN电子结构和光学性质研究[J].物理学报，2008, 57(10)：6513.

[7] Xing Haiying, Fan Guanghan, Zhang Yong, et al. First principle study of Mg,Si and Mn co-doped GaN[J]. Acta Physica Sinica, 2009, 58(1):450-458.

邢海英，范广涵，章 勇，等. 第一性原理研究Mg,Si和Mn共掺GaN[J].物理学报，2009, 58(1): 450-458.

[8] Xing Haiying, Fan Guanghan, Zhou Tianming,et al. Electronic and magnetic properties of p,n type dopant and Mn co-doped GaN[J]. Acta Physica Sinica, 2009, 58(5):3324-3330.

邢海英，范广涵，周天明.p, n型掺杂剂与Mn共掺杂GaN的电磁性质[J].Acta Phys Sin, 2009, 58(5):3324-3330.

[9] Katayama-Yoshida H, Kato R, Yamamoto T. New valence control and spin control method in GaN and AlN by codoping and transition atom doping[J]. Journal of Crystal Growth, 2001, 231(3):428-436.

[10] Wu Z M, Wang M, Deng J Q. Study on the electro-magnetic properties of Mn doped GaN diluted magnetic semiconductors[J].Journal of Atomic and Molecular Physics，2015，32(1)：129-134.

毋志民，王 蒙，邓军权. Mn掺杂GaN稀磁半导体的电磁特性研究[J].原子与分子物理学报，2015, 32(1): 129-134.

[11] Jie Weiwei, Yang Chun. The electronic structures of vacancy defects in hexagonal GaN[J]. Journal of Sichuan Normal University, 2010, 33(6):803-807.

介伟伟，杨 春.六方GaN空位缺陷的电子结构[J].四川师范大学学报，2010, 33(6):803-807.

[12] Wan Xiang，Meng Xianquan，Liu Yihe. The investigation of the morphology，crystal structure and growth mechanism of GaN nanowires synthesized by CVD[J]. Journal of Funtional Materials，2014，45(2):02082-02085.

[13] Tao Zhikuo，Zhang Rong，Chen Lin，et al. Growth and characterization of Fe/GaN and Fe3N/GaN[J]. Journal of Funtional Materials，2012，43(19):2647-2650.

[14] Liu Zhanhui，Zhang Lili，Li Qingfang，et al. Properties of GaN film grown by hydride vapor phase epitaxy[J]. Journal of Functional Materials, 2013，44(23):3412-3415.

[15] Sedhain A,Li J,Lin J Y,et al.Nature of deep center emissions in GaN [J].Appl Phys Lett,2010,96(15):151902.

[16] Xu Daqing，Zhang Yimen，Li Peixian，et al.Microstructure and optical properties of Mg-doped GaN epilayers implanted with Mn ions[J]. Journal of Applied Physics, 2015, 46(14):14019-14022.

[17] Sasaki T, Sonoda S, Yamamoto Y, et al. Magnetic and transport characteristics on high Curie temperature ferromagnet of Mn-doped GaN[J]. Journal of Applied Physics, 2002, 91(10):7911-7913.

[18] Filhol J S, Jones R, Shaw M J, et al. Structure and electrical activity of rare-earth dopants in GaN[J]. Applied Physics Letters, 2004, 84(15):2841-2843.

[19] Ryan P Davies, Abernathy C R, Pearton S J, et al. Review of recent advances in transition and lanthanide metal-doped GaN and ZnO[J]. Chemical Engineering Communications, 2009, 196(9):1030-1053.

[20] Lindan P J D. First-principles simulation: ideas, illustrations and the CASTEP code[J]. Journal of Physics Condensed Matter, 2002, 14(11):2717-2744.

[21] Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Physical Review B Condensed Matter, 1990, 41(11):7892-7895.

[22] Korotkov R Y, Gregie J M, Wessels B W. Optical properties of the deep Mn acceptor in GaN∶Mn[J]. Applied Physics Letters, 2002, 80(80):1731-1733.

[24] Liang C, Zhang J. GaN dawn of 3rd generation semiconductors[J]. Chinese Journal of Semiconductors, 1999, 20(2): 89-99.

梁春广, 张 冀. GaN—第三代半导体的曙光[J]. 半导体学报, 1999, 20(2): 89-99.

[25] Shang G, Peacock P W, Robertson J. Stability and band offsets of nitrogenated high-dielectric-constant gate oxides[J]. Applied Physics Letters, 2004, 84(1):106-108.

[26] Kronik L, Jain M, Chelikowsky J R. Electronic structure and spin polarization of MnxGa1-xN[J]. Physical Review B, 2002, 66(4):2014-2016.

[27] Sanyal B, Bengone O, Mirbt S. Electronic structure and magnetism of Mn doped GaN[J]. Physical Review B, 2003, 68(20): 205210-205216.

[28] Gerstmann U, Blumenau A T, Overhof H. Transition metal defects in group-Ⅲ nitrides: an ab initio calculation of hyperfine interactions and optical transitions[J]. Physical Review B, 2001, 63(7):247-250.

[29] Fan Yuqing,He Aling. Half-metallic properties of Mn-AlN and Cr-AlN based on first-principles[J]. Acta Physico-Chimica Sinica, 2010, 26(10): 2801-2806.

樊玉勤，何阿玲，基于第一性原理的Mn-AlN和Cr-AlN的半金属性质[J]. 物理化学学报，2010,26(10):2801-2806.

[30] Sheng X C. The spectrum and optical property of semiconductor [M].Beijing: Science Press, 2003:76.

沈学础.半导体光谱和光学性质(第2版)[M].北京：科学出版社,2003：76.

[31] Guo Jianyun, Zheng Guang, He Kehua, et al. First-principles study on electronic structure and optical properties of Al and Mg doped GaN[J]. Acta Physica Sinica, 2008, 57(6):3740-3746.

郭建云，郑 广，何开华，等. Al,Mg掺杂GaN电子结构及光学性质的第一性原理研究[J].物理学报，2008，57(6)：3740-3746.

[32] Han B, Wessels B W, Ulmer M P. Optical investigation of electronic states of Mn4+ions in p-type GaN[J]. Applied Physics Letters, 2004, 86(4):042505-1-3.

[33] Li Qianqian, Hao Qiuyan, Li Ying,et al. Theory study of rare earth (Ce,Pr)doped GaN in electronic structure and optical property[J]. Acta Physica Sinica, 2013,62(1):7103-7110.

李倩倩，郝秋艳，李 英，等. 稀土元素(Ce, Pr)掺杂GaN的电子结构和光学性质的理论研究[J].物理学报，2013,62(1):7103-7110.

First-principles study of the effects of GaN∶Mn with N vacancy and Ga vacancy on electronic structures,ferromagnetism and optical properties

JIANG Lianjiao，FU Silie，QIN Yingxing，LI Jianxiang

(Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering, South China Normal University,Guangzhou 510006, China)

The electronic structures and optical properties of Ga vacancy and N vacancy from the incorporation of Mn atoms doping as nearest neighbor,next nearest neighbor and far neighbor each of the three cases GaN systems were calculated by using plane wave ultra-soft pseudo-potential method based on density functional theory.This article analyzed and compared the effects of different positions of vacancies on the performance of magnetic properties of Mn doped GaN.The results indicate that the band gap becomes wider after Mn doped GaN,and it shows half metallic ferromagnetism.N vacancies enhance the ferromagnetism of Mn doped GaN systems and the total magnetic moment of the doped systems increases with the decrease of the N vacancy away from Mn impurity.However,Ga vacancies reduce the ferromagnetism of Mn doped GaN systems and the total magnetic moment of the doped systems decreases with the reduction of the Ga vacancy away from Mn impurity. Furthermore,the main absorption peaks and absorption edge move towards a lower energy region in all cases of vacancies of Mn doped systems,which shows a red shift phenomenon.

GaN crystal;Mn doping; vacancy; electronic strutures; optical properties

1001-9731(2016)12-12139-08

国家自然科学基金资助项目(10575039)；广东省自然科学基金资助项目(S2013010012548)

2016-03-29

2016-07-20 通讯作者：符斯列，E-mail: fusl@scnu.edu.cn

蒋联娇 (1989-)，女，湖南衡阳人，在读硕士，师承符斯列教授，从事GaN基稀磁半导体研究。

O472；O482.54

A

10.3969/j.issn.1001-9731.2016.12.023