变时滞二阶神经网络周期解的存在性和指数稳定性

邢青红

(太原工业学院 理学系,山西 太原 030008)



变时滞二阶神经网络周期解的存在性和指数稳定性

邢青红

(太原工业学院 理学系,山西 太原 030008)

文章运用Brouwer不动点定理以及构造新的Lyapunov函数得到变时滞二阶神经网络周期解的存在性和指数稳定性.

神经网络;变时滞;周期解;指数稳定

0 引言

考虑二阶神经网络的模型:

(1)

其中ai(t)>ai>0,bji(t),Tijk(t),τj(t)>0,Ii(t):R+→R是连续周期函数具有周期ω>0.

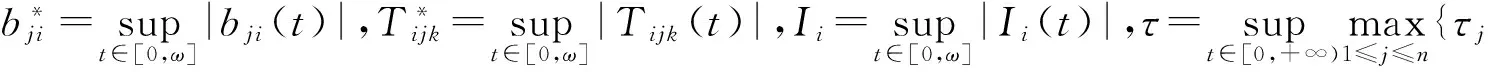
初始条件:xi(s)=φi(s),s∈[-τ,0].

(H1) 行为函数fj:R→R满足lipschz连续,即

|fj(x1)-fj(x2)|≤Lj|x1-x2|,x1,x2∈R.

(H2)存在正数Mj,使得|fj(x)|≤Mj≤M.

1 周期解的存在性和稳定性

引理1 (Brouwer不动点定理):设C是Rn中的一个紧凸子集,T:C→C是连续的,则T必有一个在C上的不动点.

引理2 (Arzela-Ascoli)为了F⊂C(M)是一个列紧集,当且仅当F是一致有界且等度连续的函数族.

定理1 假设(H2)成立,则模型(1)至少有一个周期解.

证明 设C=C([-τ,0],Rn)是Banach空间.具有范数:‖φ(x)‖=sup-τ≤θ≤0|φx(θ)|.

定义映射T从B到C=C([-τ,0],Rn),T=(φx(θ))→x(θ+ω,φ),

x(t)=(x(t),φ)是(1)的解具有起始条件xi(θ)=φi(θ),θ∈[-τ,0],

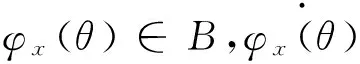
由Brouwer不动点定理,必有φ*∈B,使得T(φ*)=φ*,因此x*(t,φ*)=x*(t,Tφ*),

即x*(t,φ*)=x*(t+ω,φ*)是模型(1)的ω-周期解.

定理2 假设(H1),(H2)成立,存在常数λ>0,使得

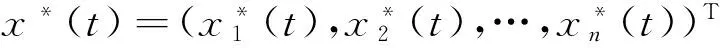
证明 由定理1得模型(1)有ω-周期解.

设(1)的任意解x(t)=(x1(t),x2(t),…,xn(t))T,

(φ1(t),φ2(t),…,φn(t))T是x(t)=(x1(t),x2(t),…,xn(t))T的初始值.

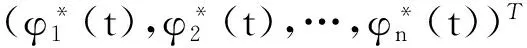
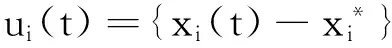
设李雅普诺夫函数V(t)=|ui(t)|eλt,则

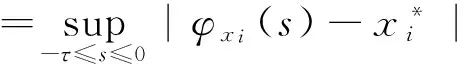
可得:|ui(t)|eλt≤K‖φx-φ*‖.t∈[-τ,0].

我们设|ui(t)|eλt≤K‖φx-φ*‖,t>0.

假设不成立,反之,则必存在i∈{1,2,…,n},ti>0,使得

|ui(t)|eλt=K‖φx-φ*‖, |ui(t)|eλt≤K‖φx-φ*‖,t∈[-τ,τi].

即|V(ti)|=K‖φx-φ*‖ , |V(t)|≤K‖φx-φ*‖ ,t∈[-τ,τi].

0≤D+(V(ti)-K‖φx-φ*‖)=D+V(ti)≤-aiK‖φx-φ*‖+

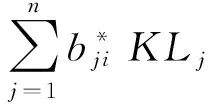
由已知0≤D+(V(ti)-K‖φx-φ*‖)<0矛盾,可得

|ui(t)|eλt≤K‖φx-φ*‖,t>0.

即V(t)=|ui(t)|eλt≤K‖φx-φ*‖,t>0.

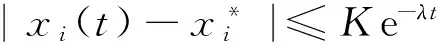
[1] 郭大钧.非线性泛函分析[M].济南:山东科学出版社,2002

[2] 钟守铭,刘碧森,王晓梅,等.神经网络稳定性理论[M].北京:科学出版社,2007:189-195

[3] HIEN L,LOAN T,HUYEN T.Existence and global asymptotic stability of positive periodic solution of delayed Cohen-Grossberg neural networks[J].Applied Mathematic and Computation,2014,240:200-212

Existence and Exponential Stability of Periodic Solution for Time-Varying Delays Two-Order Neural Networks

XING Qinghong

(Department of Science, Taiyuan Industrial College, Taiyuan 030008, China)

To use Brouwer fixed point theorem and new Lyapunov function,we can obtain the result for the existence and exponential stability of periodic solution for time-varying delays two-order neural networks

two-order neural networks; time-varying delays;periodic solution; exponential stability

2016-03-17

邢青红(1976-),女,山西运城人,硕士,太原工业学院理学系讲师,主要从事微分方程动力系统研究.

1672-2027(2016)02-0023-03

O175.13

A