非线性超声检测的因素探讨及其在HR3C烟侧腐蚀的应用

秦 鹏，李 萍，侯天宇，赵 杰，李廷举

(大连理工大学 材料科学与工程学院，辽宁 大连 116023)



非线性超声检测的因素探讨及其在HR3C烟侧腐蚀的应用

秦 鹏，李 萍，侯天宇，赵 杰，李廷举

(大连理工大学 材料科学与工程学院，辽宁 大连 116023)

基于对影响非线超声性检测因素的探讨，考察了应用非线性检测无损评价HR3C烟侧腐蚀的可行性。结果表明：脉冲激励串个数n≤2df/c，加汉宁窗有助于降低系统干扰，此外，样品表面粗糙度对非线性系数β产生显著的影响。随腐蚀时间的延长，非线性系数呈现阶段性的递增趋势。腐蚀初期(腐蚀时间在50h以内)，非线性系数增幅不足20%；然而，腐蚀至150h，非线性系数显著增加；相对于未腐蚀样品，腐蚀200h时的非线性系数增幅达260%。非线性系数的单调变化与腐蚀损伤的加剧相一致，因此，应用超声非线性无损评价HR3C的烟侧腐蚀是可行的。

非线性超声检测；非线性系数；烟侧腐蚀

伴随着超超临界发电技术的推广应用，超超临界用钢得到长足的发展。HR3C因其良好的抗高温氧化性以及持久强度被用于制造超超临界发电机组的锅炉管道[1,2]。鉴于国内燃煤中含有相当数量的S,Cl,Na,K等元素，煤燃烧过程中形成的碱金属(K,Na)盐类在高温条件下通过与含S化合物作用，发生硫酸盐熔融；熔融的硫酸盐通过向内扩散，破坏氧化层，使基体HR3C发生烟侧腐蚀[3,4]。烟侧腐蚀速率快，腐蚀区域相对集中，导致管壁减薄[5,6]，引发爆管事故，进而威胁电厂安全运行，对服役期间的超超临界发电机组的连续安全运行形成严峻的考验，而常规的检测方法由于原理的局限性无法完成对早期烟侧腐蚀的无损检测和表征。因此，如何对超超临界用钢HR3C烟侧腐蚀程度进行检测已成为超超临界机组发展亟待解决的问题。

研究表明：材料内部存在的微小缺陷可激发超声波传播过程的非线性行为[7]，且由于非线性超声检测自身的特点，其对于材料的早期缺陷更为敏感[8-10]，超声非线性参量可以用于描述固体介质非线性的相对变化，尤其是对材料的早期高温损伤方面具有潜在优势。徐从元等[11]通过测量不同损伤程度下LY-12铝合金棒的声速、衰减及非线性系数，证明了非线性系数对疲劳损伤的敏感程度要高于声速和衰减；Nagy[12]使用超声非线性系数对材料的早期疲劳程度进行了无损表征，指出随着疲劳次数的增加, 非线性系数明显增加, 但是线性参数(衰减、声速等)却没有发生明显变化；江念等[13]对复合结构件进行了非线性超声检测，并完成了对于粘接效果的无损表征，明确了非线性效应程度可以作为有效评价复合结构粘接质量的特征参数；邓明晰等[14]通过考查不同材料的板材、工作频率、板厚以及入射角改变等因素对兰姆波模式的影响, 利用非线性兰姆波实现了对层状固体结构表面性质的变化情况的无损表征。

综合透射法具有操作简单且能量衰减小以及非线性超声检测对于材料早期性能衰退以及微观缺陷具有较高敏感性的特点[15]。本工作首先探讨了发射脉冲模式、脉冲激励串个数、加窗处理、输入电压峰峰值和样品粗糙度对非线性超声检测的影响；并在此基础上，开展了应用非线性超声透射法对超超临界用钢HR3C烟侧腐蚀无损检测可行性的研究与分析。

1 非线性超声检测的原理

传统超声检测使用的超声波能量低、波幅度小, 即由超声波传播时产生的应力和应变均较小, 此时介质中超声波的传播遵循线性应力-应变关系，倍频信号分量可以忽略不计。当使用能量较高，波幅较大的超声波进行检测时, 超声波在传播过程中受到介质中应力-应变非线性的影响增强, 非线性响应信号分量能量增强、幅值变大, 此时超声波的波形会发生明显的失真现象，倍频信号分量将不可忽略不计。

Breazeale等[16]从连续介质模型出发, 得到了一维纵波非线性波动方程：

(1)

式中：K2表示在一维波沿x方向传播情况下，材料的二阶弹性模量，为常用的材料弹性模量，用于表征固体材料的线弹性性质；K3为三阶弹性模量，受材料内部微观组织的影响，可表征固体中的非简谐性[17]。

定义非线性系数β：

β=-(3K2+K3)/K2

(2)

以最简单的一列正弦超声波在各向同性固体中传播为例, 即：

u(x,t)=A0sinϖ t

(3)

其二级近似解为:

(4)

式中：ω为角频率;x为传播距离;t是时间；k=ω/c0；为波数。

由此求出超声非线性系数：

(5)

进一步的研究表明：向含有损伤的材料中入射正弦波时，固体内部的不均匀性如空隙、位错等微观缺陷的两接触界面会随着波形的振动往复开闭,会使两接触面互相重复打击及相互摩擦，产生显著的倍频谐波[19]，进而造成波形的畸变，使非线性系数发生变化，二者存在对应关系。换言之，超声非线性系数反映了当波穿过非线性材料时波形发生畸变的程度，可用于材料及结构微细损伤的非破坏检查与评价。

2 实验方法

2.1 非线性超声检测系统

实验所用基于透射信号的非线性超声检测系统如图1所示，该系统由RAM-SNAP系统、高能匹配电阻、衰减器、滤波器、信号取样器、换能器、夹具、示波器及计算机等组成。RAM-SNAP系统输出频率为5MHz的高能量正弦脉冲循环串信号，经过50Ω匹配电阻、固定衰减器、低通滤波器等模块后加载到标称频率5MHz、晶片直径10mm的发射探头，信号经耦合剂垂直入射到待检试件，工件和探头之间使用特制夹具进行固定；透射信号被固定在试件另一端面的标称频率10MHz、晶片直径10mm的探头接收进入系统通道。在此系统中，为了滤除输入信号中的高频谐波分量，引入了低通滤波器，确保激励发射换能器的信号为单一频率的正弦波。

2.2 研究对象和样品制备

实验过程中为了能够准确反应测试参数对于系统本身非线性的影响，采用 CSK-Ⅰ型标准试块作为研究对象，探讨了脉冲串个数、加窗处理、输入电压以及表面粗糙度等对非线性超声检测的影响，进而确定发射信号参数的选择原则。

烟侧腐蚀所用材料取自于HR3C炉管，将其加工成 15mm×15mm×7mm的片状试样，表面统一用水砂纸打磨至400#，保证样品表面具有相同的粗糙度，然后用丙酮和乙醇清洗并吹干。采用热喷涂法在试样表面喷涂一层硫酸盐的饱和溶液。硫酸盐成分为w(Na2SO4)∶w(K2SO4)=8∶5，硫酸盐的组成及配比是根据国内二十几家电厂煤粉成分分析的结果，取其中K2O和Na2O平均值的摩尔比确定的，与锅炉管道工作环境的沉积盐相类似[20]。试样表面的硫酸盐量为5mg/cm2。将喷涂硫酸盐的试样放在坩埚中进行热腐蚀实验，腐蚀温度为750℃，腐蚀时间分别为20,50,100,150,200h。为了排除不同表面粗糙度对非线性系数的影响，腐蚀之后进行超声清洗，除去表面的氧化层。

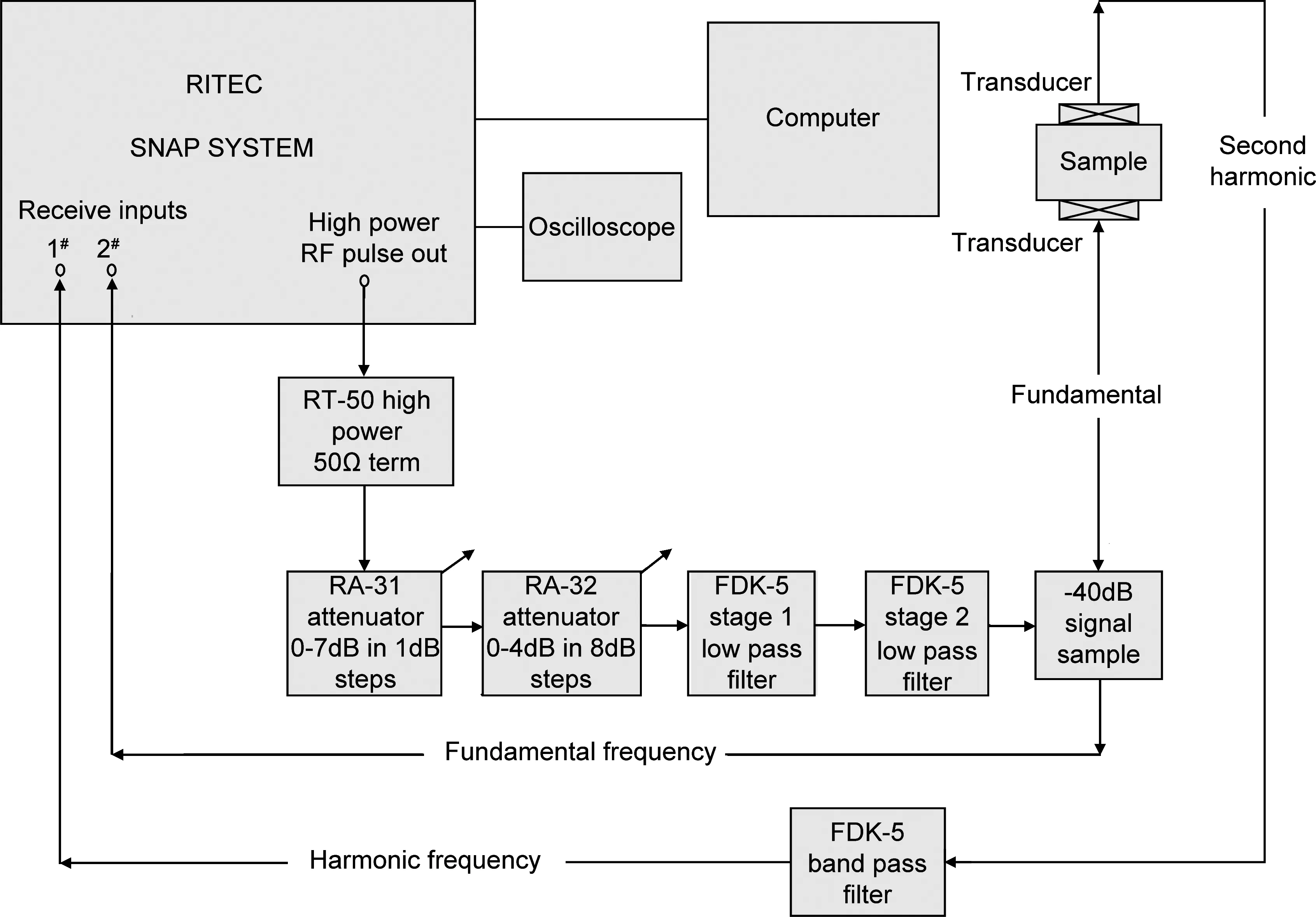
图1 非线性超声检测系统框图

3 影响非线性超声检测的因素探讨

在非线性超声检测中，接收信号由系统内部的随机噪声信号和带有试样信息的反射/透射信号相互叠加而成。当系统内部的随机噪声较大时，会影响甚至湮没有效信号，造成结果的不稳定和错误。为了准确提取能够表征材料状态的非线性特征信号，要求仪器和随机因素产生的谐波干扰尽可能减少，使发射信号的频率成分尽可能简单，这就需要对发射信号的参数进行合理选择和设置。

3.1 非线性超声检测信号模式的选择

非线性超声检测不仅要求输入信号的功率高，而且频率成分要尽可能的单一，但高功率连续波通常难以实现，且在该激励模式下的轴向分辨力低，无法对缺陷进行准确定位；如采用单脉冲模式作为激励方式，激励波形幅值很大，检测轴向分辨力高，但单脉冲信号本身频率范围较宽，不利于判断接收信号中所包含的谐波频率成分是由材料的非线性效应所引起的还是在发射端引入的，从而影响测量结果。基于上述原因，介于连续波和单脉冲之间的脉冲串模式在非线性超声检测领域得到了广泛应用，该模式下输出的发射信号具有输出功率较高、频带较窄，且轴向分辨力相对较好的特点。

3.2 脉冲激励串对非线性超声检测的影响

进行非线性超声检测时，为了确保回波信号之间能够相互区分开来，要求接收信号的脉冲激励串长度应小于二次回波间的时间间隔，因此，需要合理选择脉冲激励串的数目。对于厚度为d，声速为c的试样，两次回波之间的声程差为2d/c，假设探头的频率为f，则每个脉冲激励串所能延续的时间为t=1/f，所以，能够区分两次回波的脉冲激励串个数，即允许的最大脉冲激励串个数为：

n=(2d/c)/(1/f)=2df/c

(6)

实验所用CSK-Ⅰ试块厚度为25mm，声速为5930m/s，发射探头的频率为5MHz，可以算出其允许的最大脉冲激励串个数n为42，考虑到传播过程中波形的畸变，所以本次实验采用的脉冲激励串个数上限为30。

非线性系数β随脉冲激励串个数变化如图2所示。由图2可以看出，随着脉冲串的增加，β呈指数规律单调递减。当脉冲激励串个数从5增加到30时，β的降幅为92.76%，这意味着进行非线性超声检测时，选择脉冲激励串的个数越多，超声信号中谐波成分所占比例越来越小，这对减小系统干扰是有利的。

图2 脉冲激励串个数对β的影响

图3 对应不同脉冲激励串的幅频分布曲线

图3描述了含有不同脉冲激励串的发射信号的幅频曲线。由图3可知：脉冲激励串越多，幅值越高，主频(5MHz)带宽越窄，由0.6MHz(cycle=10)减小到0.2MHz(cycle=30)。分析认为：脉冲串的增加，意味着发射能量的增加，而在增加的这部分能量中5MHz占绝大部分，这使得5MHz的频谱分量增加得更显著，A1(主频幅值)增幅为197.4%，A2(倍频幅值)增幅仅为78.24%。

综上所述：进行非线性超声检测时，允许的脉冲激励串个数n≤2df/c；较多的脉冲串个数有助于减小倍频幅值在发射信号能量中所占的比例，有利于降低系统干扰。

3.3 加窗处理对非线性超声检测的影响

超声换能器频带宽度有限，为了充分利用换能器的频带，可以通过利用窗函数的频率特性，降低旁瓣电平，确保发射信号的频谱与换能器的固有频带相符。为此，需要对发射信号进行适当的加窗处理，进而减少因为发射信号的非线性对于最终结果的影响。汉宁窗因具有良好的频率分辨率，可以降低频率泄漏[21]，所以本实验采用了汉宁窗来探究发射信号的加窗处理对于非线性超声检测的影响。

加窗处理对非线性超声检测的影响如图4所示。从图4看出，加窗处理使包含相同脉冲激励串的发射信号的非线性系数β显著降低；当脉冲激励串个数小于15时，加窗能够明显降低β，降幅可达200%；当脉冲激励串进一步增加到30时，加窗作用使β降低50%左右。

图4 加窗处理对非线性系数β的影响

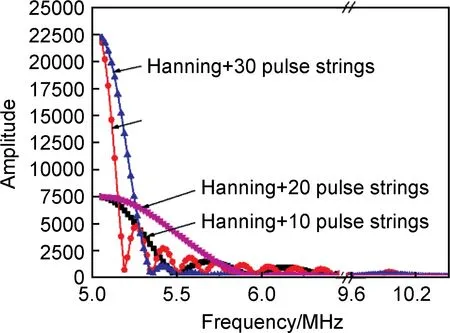
图5 对应不同脉冲串的幅度-频谱曲线

图5描述了包含不同脉冲激励串的发射信号加窗处理后的幅度-频谱曲线，显而易见，加窗处理主要是对倍频幅值产生显著的作用。经汉宁窗调制处理，接收信号的主频幅值A1变化不大，但倍频幅值A2明显下降，对于具有相同脉冲激励串的发射信号，加窗之后接收信号中A1的降幅仅为5%左右，但A2的降幅达到了50.78%以上；相当于通过汉宁窗对发射信号进行一次滤波降噪，降低了主频之外的旁瓣信号能量，从而降低了接收信号中的杂波的干扰，使信号成分变得更加纯净。

此外，当脉冲激励串个数增加时，加窗处理的作用会减弱。当脉冲激励串个数为5时，加窗处理后β的降幅达到了75.42%，当脉冲激励串个数增加到30时，加窗处理后β的降幅则为47.68%。分析认为，在较少脉冲激励串时，由于信号本身的能量较低，即A1也较小，加窗处理后A2的变化对非线性系数的作用较为突出。脉冲激励串的增加意味着发射能量的增加，此时A1呈现大幅度上升，虽然加窗处理可以减小A2的增幅，但对β的降幅相对减小。

综上所述，进行非线性超声检测时，对发射信号进行加窗处理可以降低测试系统自身的非线性，有利于保证实验结果的稳定性和准确性。

图6 输入电压对A1和A2的影响

3.4 输入电压峰峰值对非线性超声检测的影响

从一维纵波非线性波动方程的二阶近似解可以看出，倍频信号幅值与基频信号幅值的平方呈线性关系。为了确保从接收信号中提取出倍频信号的幅值，在非线性的测量过程中要求输入信号的能量应尽可能高一些，但增大输入电压峰峰值(VPP)也会造成接收信号波形存在一定程度的畸变，造成基频幅值A1和倍频幅值A2的波动，如图6所示。当输入电压峰峰值(VPP)变化时，通过10MHz带通滤波器的接收信号基频幅值A1和倍频幅值A2均发生变化，进行曲线拟合，发现A1与电压峰峰值呈线性关系，相关度可达0.9952，而A2与电压峰峰值则成二次曲线关系，相关度可达0.9965。为此需要考察输入电压峰峰值(VPP)对非线性系数的影响。输入电压峰峰值对非线性系数β的影响如图7所示。由图7看出，当输入电压峰峰值改变时，非线性系数β存在一定的波动，但这种波动较小且在均值(μ)的三倍方差(σ)范围之内。实际检测中表现为当系统的输入电压峰峰值发生变化，非线性系数的变化在误差允许范围之内。这意味着，输入电压峰峰值参数对系统本身的非线性影响较小。

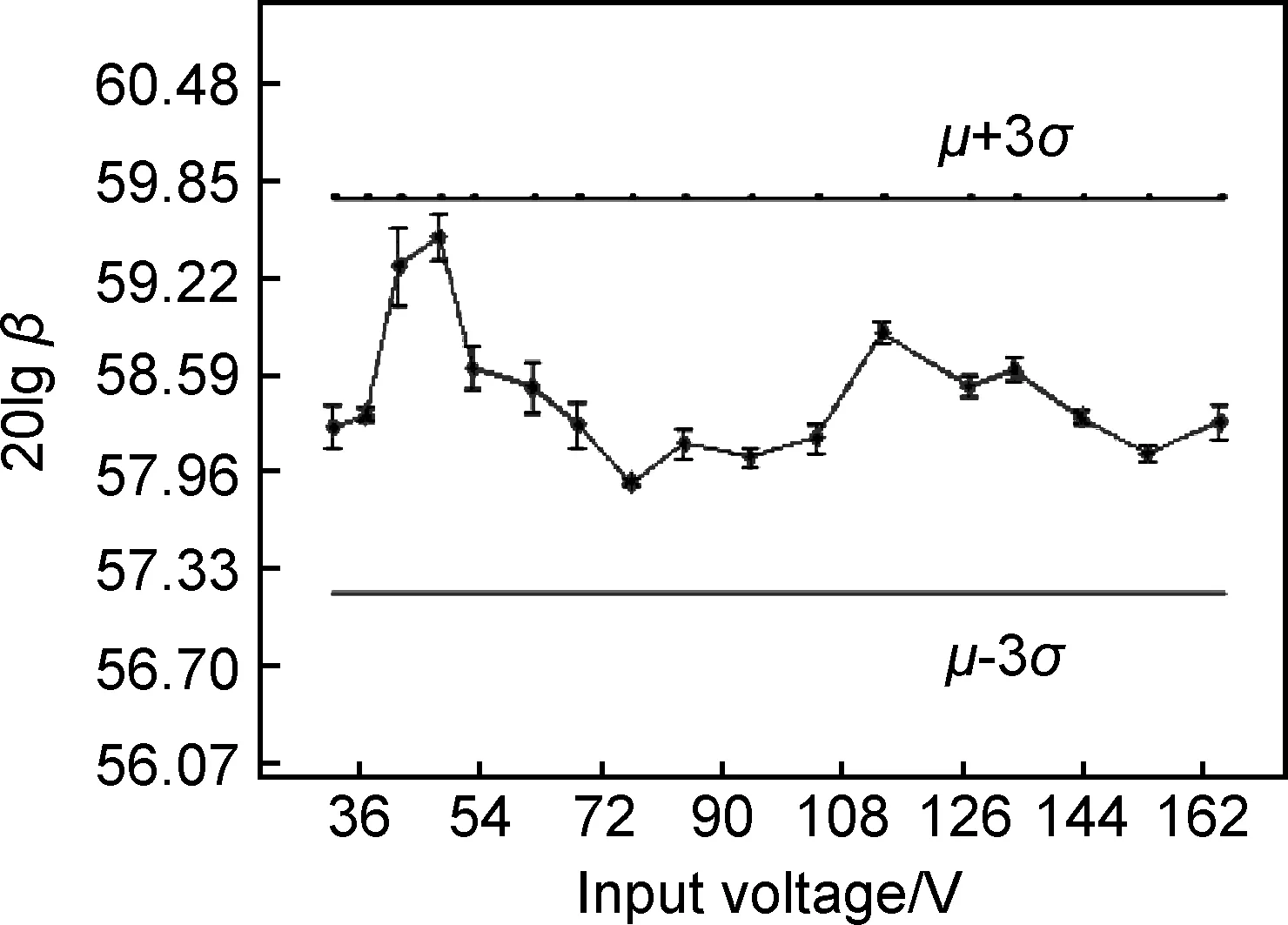
图7 输入电压对β的影响

因此，在非线性超声检测过程中，综合考虑保证接收信号的能量和降低系统非线性的影响，应在探头不被击穿的前提下，宜采用较高输入电压峰峰值。

3.5 样品表面粗糙度对非线性超声检测的影响

图8 粗糙度对非线性系数的影响

实际检测过程中，样品表面粗糙度存在一定程度的差异，将对超声非线性产生显著影响。为了考察表面粗糙度对非线性系数β的影响，实验采用不同型号(200#～1000#)的砂纸打磨处理试样表面，根据表面粗糙度对照表得出样品表面对应的粗糙度，在相同的实验条件下测定其非线性系数β的变化，每组数据测量5次。得到表面粗糙度随非线性系数变化规律如图8所示。从图8可以看出：随着样品表面粗糙度的增加，非线性系数β单调递增。由于波长量级(mm)远大于表面粗糙度量级(μm)，因此可以忽略散射的影响。分析认为：样品表面粗糙度改变，相当于样品表面存在不同程度的微观缺陷和不连续。当高功率的超声波作用于粗糙的样品表面时，不连续界面两侧会随着波形的振动发生往复开闭，从而产生显著的高频谐波。因此，样品表面粗糙度的增加可以被看作是表面微观缺陷或不连续尺寸的增大，这将导致非线性效应的增强，表现在β呈现上升的趋势。

总之，样品表面的粗糙度对非线性系数β产生正相关的影响，所以在非线性超声检测时，样品表面粗糙度要求尽量一致。

4 HR3C烟侧腐蚀非线性超声检测的实验结果与分析

HR3C在750℃腐蚀20，100h的截面形貌如图9所示。由图9可见：高温腐蚀后样品表面形成了疏松多孔的腐蚀层，腐蚀层与基体产生不同程度的剥离，在制样过程中局部出现脱落；近基体侧的氧化层则相对致密，连续性较好；临近氧化层的基体中有长度不等的裂纹及数量不同的孔洞生成；随着腐蚀时间的延长，裂纹长度逐渐增大，孔洞数量逐渐增多。

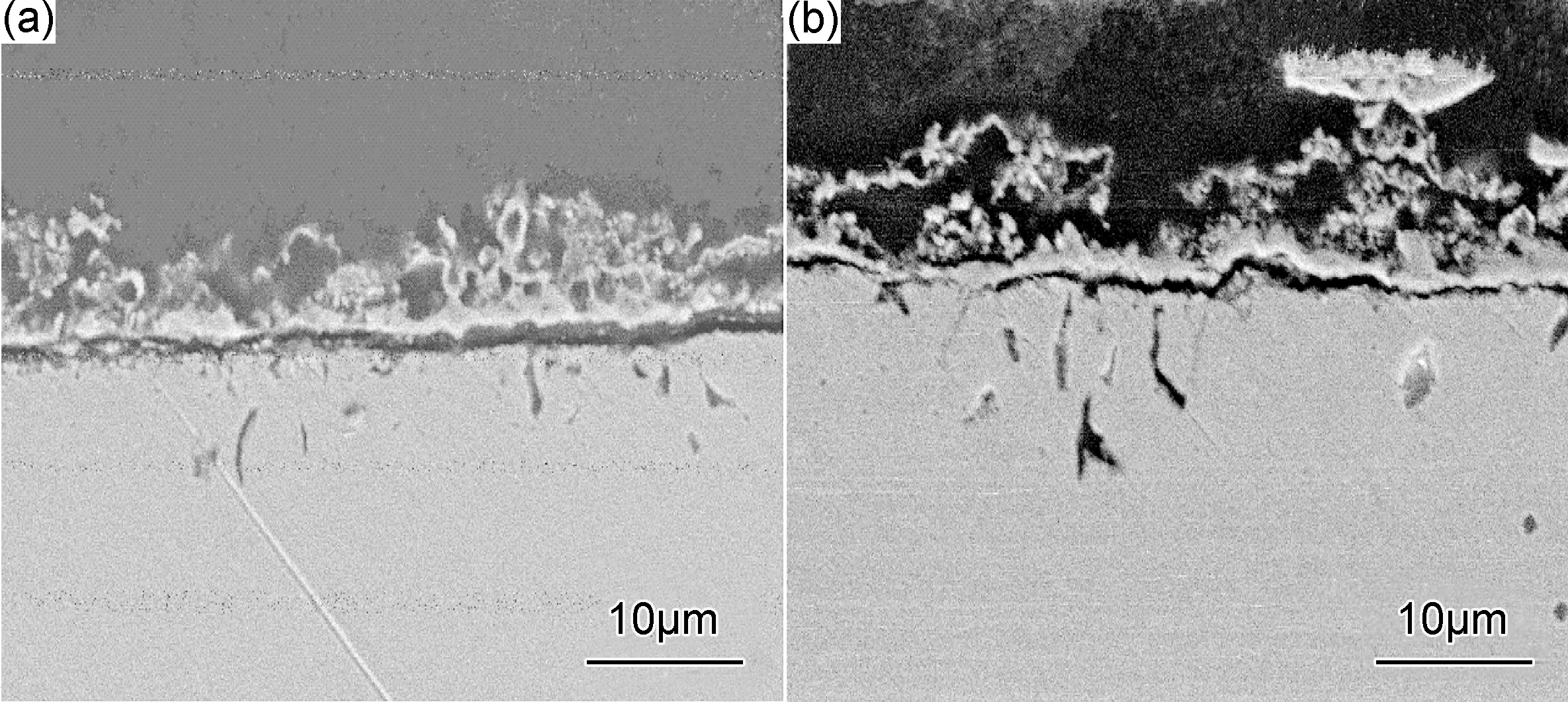
图9 HR3C在750℃腐蚀20h (a)和100h (b)的截面形貌

根据式(6)，计算出理论最大脉冲激励串的个数为11个，考虑到实验的实际条件，在实验中采用脉冲激励串个数为7个，对发射信号进行汉宁窗处理，输入电压峰峰值VPP为204V。为了能够准确提取倍频信号，接收信号通过10MHz带通滤波器。样品表面超声清洗去除剩余盐膜和氧化层，每个样品测量5次，探头和试样之间采用蜂蜜耦合, 忽略耦合剂带来的非线性影响。

实验中测出接收信号中基频幅值A1和倍频幅值A2的变化如图10所示。

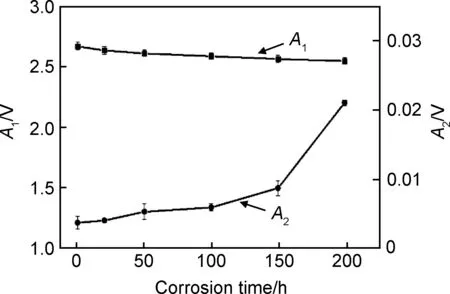
图10 A1,A2随腐蚀时间变化曲线

从图10可以看出，随着腐蚀时间的延长，腐蚀程度越来越严重，这对超声波信号的线性传播是存在一定影响的，具体表现为A1呈现单调递减的趋势，相比较未腐蚀试样，200h腐蚀样品的基频幅值降低了10.7%；而其非线性行为表现为A2呈现单调递增的趋势，200h腐蚀样品的倍频幅值升高至未腐蚀样品的178.4%。

图11 β随腐蚀时间变化曲线

计算不同腐蚀样品的非线性系数，将不同腐蚀时间的样品非线性系数(βi)与未腐蚀式样的非线性系数(β0)，进行归一化处理，得到样品的归一化非线性系数β随腐蚀时间变化如图11所示。随腐蚀时间的延长，β呈现阶段性单调递增的趋势。对应腐蚀的不同阶段β变化具体如下：腐蚀时间在50h以内，腐蚀速率较慢，腐蚀处于孕育期，样品表面并没有发生太大的变化，相比较未腐蚀的样品，β变化不大，增幅在20%以内；增加腐蚀时间到150h时，腐蚀层表面的孔洞增加，有少量微裂纹的产生，腐蚀进入均匀发展阶段，β较孕育期的要更大，呈现线性增加，增幅可达未腐蚀试样的80%；延长腐蚀时间到200h时，腐蚀层的表面已经出现了明显向内延伸的微裂纹和孔洞，这种现象加速了腐蚀的进行，此时腐蚀层的表面对声波的非线性传播带来更大的促进作用，表现为β增幅显著，达到未腐蚀试样的260%。

综上所述，随着腐蚀时间的延长，腐蚀程度加重，非线性系数是呈现递增趋势，因此，选择非线性系数作为特征参数判断腐蚀程度，可以通过非线性系数的大小来判断腐蚀的程度，通过非线性系数的增幅来判断腐蚀的阶段。

5 结论

(1)脉冲激励串的个数n不多于2df/c；适当增加脉冲激励串个数和对发射信号采用Hanning窗处理，均有利于降低系统的干扰；样品表面粗糙度对非线性系数β产生正相关的影响。

(2)随腐蚀时间的延长，非线性系数呈现阶段性的单调递增趋势。腐蚀初期(腐蚀时间在50h以内)，非线性系数增幅不超过20%；腐蚀至150h，非线性系数显著增加；相对于未腐蚀样品，腐蚀200h时的非线性系数增幅达260%。

(3)非线性系数的单调变化与腐蚀损伤的加剧相一致，因此，应用超声非线性无损评价HR3C的烟侧腐蚀是可行的。

[1] 杨素宝. 超(超)临界火电机组用钢数据库的开发及其应用[D]. 昆明: 昆明理工大学, 2009.

YANG S B. Study and application of database for steels used in USC power plants [D]. Kunming: Kunming University of Science and Technology, 2009.

[2] 张俊峰, 王黎明. 超超临界压力锅炉高温部件材料简析[J]. 发电设备，2009，23(6)：461-463.

ZHANG J F, WANG L M. Material analysis for high-temperature components of ultra supercritical pressure boilers [J]. Power Equipment，2009，23(6)：461-463.

[3] VISWANATHAN R, SARVER J, TANZOSH M J. Boiler materials for ultra-supercritical coal power plants steam-side oxidation[J]. Journal of Materials Engineering and Performance，2006，15(3)：255-274.

[4] WANG C J, CHENG Y C, SU Y H. The hot corrosion of Fe-Mn-Al-C alloy with NaCl-Na2SO4coating mixtures at 750℃[J]. Oxidation of Metals，2003，59(1-2)：115-133.

[5] 赵双群, 谢锡善，GAYLORD D S. 粉煤燃烧环境中过热器管的高温腐蚀[J]. 特殊钢，2003，24(6)：36-39.

ZHAO S Q, XIE X S, GAYLORD D S. High temperature corrosion of super-heater tube materials in pulverized coal-fired environment [J]. Special Steel，2003，24(6)：36-39.

[6] 齐慧滨, 郭英倬, 何业东, 等. 燃煤火电厂锅炉“四管”的高温腐蚀[J]. 腐蚀科学与防护技术，2002，14(2)：113-116.

QI H B, GUO Y Z, HE Y D, et al. High temperature corrosion in boilers of coal fired power plants [J]. Corrosion Science and Protection Technology，2002，14(2):113-116.

[7] 税国双, 汪越胜, 曲建民，等. 材料力学性能退化的超声无损检测与评价[J]. 力学进展，2005，35(1)：52-68.

SHUI G S, WANG Y S, QU J M, et al. Advance in nondestructive test and devaluation of material degradation using nonlinear ultrasound [J]. Advance in Mechanics，2005，35(1)：52-68.

[8] JHANG K Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: a review [J]. International Journal of Precision Engineering and Manufacturing，2009，10(1)：123-135.

[9] FROUIN J, SATHISH S, MATIKAS T E, et al. Ultrasonic linear and nonlinear behavior of fatigued Ti-6Al-4V[J]. Journal of Materials Research，1999，14(4)：1295-1298.

[10] CANTRELL J H, YOST W T. Nonlinear ultrasonic characterization of fatigue microstructures [J]. International Journal of Fatigue，2001，23(1)：487-490.

[11] 徐从元, 姜文华. 疲劳金属材料非线性声学特性的实验研究[J]. 南京大学学报(自然科学版)，2000，36(3)：328-335.

XU C Y, JIANG W H. Experimental investigation on acoustic nonlinearity of fatigued metals [J]. Journal of Nanjing University(Natural Sciences)，2000，36(3)：328-335.

[12] NAGY P B. Fatigue damage assessment by nonlinear ultrasonic materials characterization[J]. Ultrasonics，1998，36(1)：375-381.

[13] 江念, 王召巴, 金永,等. 复合结构界面粘接质量的非线性超声检测[J]. 兵工学报，2014，35(3)：398-402.

JIANG N, WANG Z B, JIN Y, et al. Measurement of interface bond quality of composite structure using nonlinear ultrasound [J]. Acta Armamentarii，2014，35(3)：398-402.

[14] 邓明晰, 裴俊峰. 无损评价固体板材疲劳损伤的非线性超声兰姆波方法[J]. 声学学报，2008，33(4)：360-369.

DENG M X, PEI J F. Nondestructive evaluation of fatigue damage in solid plates using nonlinear ultrasonic Lamb wave method [J]. Acta Acustica，2008，33(4)：360-369.

[15] 敦怡, 师小红, 王广龙, 等. 微纳米级裂纹的非线性超声检测[J]. 光学精密工程，2011，19(1)：132-137.

DUN Y, SHI X H, WANG G L, et al. Nonlinear ultrasonic test of micro-nano crack [J]. Optics and Precision Engineering，2011，19(1)：132-137.

[16] BREAZEALE M A, PHILIP J. Determination of Third-order Elastic Constants from Ultrasonic Harmonic Generation Experiments [M]. New York：Physical Acoustics XVII, Academic Press,1984.1-60.

[17] 顾惠成, 王汝菊, 王积方. YAG:N_d～(3+)单晶的二阶和三阶弹性常数[J]. 声学学报，1994，19(3)：196-201.

GU H C, WANG R J, WANG J F. The elastic behavior of YAG:N_d～(3+)crystal under pressure[J]. Acta Acustica，1994，19(3)：196-201.

[18] 弓飞. 金属材料拉伸变形下的超声非线性特性研究[D]. 北京：北京交通大学，2010.

GONG F. Research on ultrasonic nonlinearity of metallic materials under tensile deformation [D]. Beijing: Beijing Jiaotong University，2010.

[19] 常俊杰, 孙德平, 林成新, 等. 超声波的非线性对涂层材料的质量评价[J]. 大连海事大学学报，2008，34(增刊1)：7-10.

CHANG J J, SUN D P, LIN C X, et al. Quality evaluation of coating materials with micro damage by ultrasonic nonlinearity [J]. Journal of Dalian Maritime University，2008，34(Suppl 1)：7-10.

[20] 霍平, 王建平. 电厂锅炉水冷壁防护涂层的抗高温腐蚀性能研究[J]. 锅炉技术，2009，40(3)：58-61.

HUO P, WANG J P. Anti-corrosion of FeCrAl and NiCr alloy coat of water wall on high temperature [J]. Boiler Technology，2009，40(3)：58-61.

[21] 曾昱. 超声非线性的理论与实验研究[D]. 北京: 北京交通大学，2008.

ZENG Y. Theoretical and experimental studies of nonlinear ultrasonic [D]. Beijing: Beijing Jiaotong University，2008.

--------------------●

Factors of Nonlinear-ultrasonic Detection and Its Application to HR3C Fireside Corrosion

QIN Peng，LI Ping，HOU Tian-yu，ZHAO Jie，LI Ting-ju

(School of Materials Science and Engineering,Dalian University of Technology,Dalian 116023，Liaoning,China)

Based on the discussion of the factors influencing the nonlinear ultrasonic testing, the feasibility of nondestructive evaluation of HR3C fireside corrosion was investigated using nonlinear ultrasonic testing. The results show that the number of pulse string is no more than 2df/cand the installation of Hanning window is helpful to reduce the disturbance of the system, in addition, the rough surface of the sample has a significant impact on the nonlinear parameterβ. The nonlinear coefficient demonstrates a phased growth trend as corrosion time prolongs. At the initial stage of corrosion(within 50h)，there are small increments within 20% in the nonlinear coefficient, however，the nonlinear coefficientβis increased obviously with the duration time to 150h. Compared with un-corroded sample, the amplification in the sample corroded for 200h reaches to 260%. The monotonous varieties in nonlinear coefficient are consistent with the aggravation of corrosion damage，hence，it is feasible to nondestructively evaluate HR3C fireside corrosion by means of ultrasonic nonlinear testing.

nonlinear ultrasonic detection；nonlinear coefficient；fireside corrosion

10.11868/j.issn.1001-4381.2016.11.015

O421.5;O422.7

A

1001-4381(2016)11-0088-08

国家自然科学基金项目(51134013，51171037)

2014-12-15;

2016-07-20

李萍(1969-)，女，副教授，博士，现研究方向为材料无损检测与评价，联系地址：大连理工大学材料科学与工程学院(116023), E-mail：liping69@dlut.edu.cn