考虑水浸温度影响的复合材料吸湿动力学模型

回 丽，王勇刚，许 良，马少华，张 旭，费昺强

(1 沈阳航空航天大学 机电工程学院，沈阳 110136；2 沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室，沈阳 110136)



考虑水浸温度影响的复合材料吸湿动力学模型

回 丽1,2，王勇刚1，许 良1，马少华1，张 旭1，费昺强1

(1 沈阳航空航天大学 机电工程学院，沈阳 110136；2 沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室，沈阳 110136)

研究了在恒温水浸吸湿实验中，水浸温度对复合材料吸湿参数的影响。通过对国产碳纤维/双马复合材料在60，70，80℃恒温水浸中进行的吸湿实验，得到了不同水浸温度下的吸湿曲线。由吸湿曲线分别求出了各水浸温度下的扩散系数和平衡吸湿率以及它们与水浸温度的关系。结合Arrhenius关系和Fick定律，得到了反映此复合材料在任意水浸温度下吸湿行为的吸湿模型。该吸湿模型能较为准确地预测此复合材料在95℃恒温水浸中任意时刻的吸湿量及预估达到特定吸湿量所需要的时间。

复合材料；Arrhenius关系；Fick定律；吸湿模型

碳纤维增强树脂基复合材料由于比强度比刚度高、耐高温、耐腐蚀、耐疲劳、可设计性强、工艺性好等优点，已成为航空航天飞行器结构中最常用的一种高性能复合材料[1-3]。然而吸湿行为对复合材料的力学性能有很大危害[4-8]。碳纤维增强树脂基复合材料吸湿行为的主要机制是水分扩散过程，吸湿过程主要受环境温度和湿度的影响。复合材料吸湿行为的研究，对预测复合材料结构的使用寿命等都有非常重要的意义[9]。大量研究[10-14]表明，碳纤维增强树脂基复合材料吸湿的初始阶段符合Fick第二定律。另外，也有学者通过实验发现纤维增强树脂基复合材料吸湿的初始阶段吸水性也符合Arrhenius关系[15]。

传统的方法是通过吸湿实验对复合材料的吸湿行为进行研究，由于复合材料层合板的各向异性特征以及碳纤维不吸湿而基体吸湿，传统实验方法周期长，效率低，得到的数据也较分散。本工作通过对国产碳纤维/双马复合材料在60，70，80℃恒温水浸中进行的吸湿实验，绘制不同水浸温度下的吸湿曲线，从而得到吸湿扩散系数D和平衡吸湿率M∞，结合Arrhenius关系和Fick第二定律，便可得到预测任意温度下该材料任意时刻吸湿量的计算模型，这为研究水浸温度对复合材料吸湿的影响提供了一定的理论指导，为进一步的寿命预测提供了依据，以便对复合材料的性能做出预判。

1 实验方法

材料：实验采用由热压罐工艺制备的国产碳纤维/双马复合材料，铺层方式为：[90]16，单层厚度为0.125mm，试样尺寸为250mm×36mm×2mm。

设备：DHG-9140A电热恒温鼓风干燥箱，LHS-100CH恒温恒湿箱，ALC-210.4电子天平。

吸湿实验：将试样放置于电热鼓风干燥箱中烘去水分，调节至工程干态W0。采用水浸加速实验法，将已脱去水分的试样分别置于60，70，80℃恒温水浴槽内进行吸湿实验。开始时每隔1h称量一次试样质量，12h后每隔12h测一次质量，以后依次延长至一到两天测量一次。称量时先用滤纸擦干表面的水分，再用电子天平称重。记录测量值为Wt，称完后将试样迅速放回恒温水浴槽内，吸湿周期通过平衡吸湿法确定。参照ASTM D 5229/D 5229M-1992(2004) 标准《聚合物基复合材料吸湿性能和浸润平衡的标准实验方法》，吸湿率可按式(1)计算：

Mt=(Wt-W0)/W0×100%

(1)

式中：Mt为t时刻试样的吸湿率(%)；Wt为t时刻试样的质量(g)；W0为试样吸湿前工程干态质量(g)。

经过长期的测定，当连续两次称重时，都满足平均吸湿量的变化小于0.01%时，则认为试样达到了有效吸湿平衡。

2 结果与分析

2.1 吸湿动力学计算模型的拟合

分别绘制此复合材料在不同水浸温度下的吸湿Mt-t1/2曲线如图1所示。

图1 复合材料分别在60，70，80℃的吸湿曲线

从实验所得的水浸吸湿曲线可以看出，在吸湿的初始阶段，由于复合材料本身的缺陷和树脂本身吸水，在温湿度的共同作用下，水分子在复合材料中的扩散速率很快，曲线的梯度较大，且水浸温度越高，吸湿速率越快。此时复合材料的吸湿率和t1/2成线性关系。随着吸湿时间的延长，吸湿速率逐渐减慢，最后趋于零达到吸湿平衡。由此可以得出水分在复合材料中的扩散符合Fick定律。在吸湿的初始阶段，可以用Fick第二定律来描述水分的扩散行为：

∂M/∂t=D×(∂2M/∂2z)

(2)

式中：D为扩散系数(mm2/h)；M为吸湿率(%)；t为吸湿时间(h)；z为试样厚度方向。

分离变量得：

(3)

式中：M0为初始吸湿率(%)；M∞为平衡吸湿率(%)；h为试样的厚度(mm)。这里M0=0，则：

(4)

根据吸湿曲线线性部分，可算得扩散系数D：

(5)

式中：Mt1为t1时刻试样的吸湿率(%)；Mt2为t2时刻试样的吸湿率(%)。

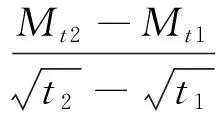
根据吸湿实验计算出不同水浸温度下表征此复合材料吸湿行为的两个重要参数值：平衡吸湿率M∞和扩散系数D。计算结果如表1所示。

表1 平衡吸湿率M∞和扩散系数D与水温T的关系

Table 1 Balanced moisture content and diffusion coefficientversustemperature

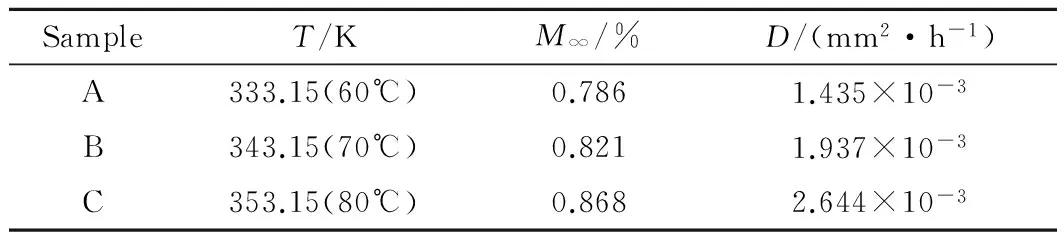
SampleT/KM∞/%D/(mm2·h-1)A333.15(60℃)0.7861.435×10-3B343.15(70℃)0.8211.937×10-3C353.15(80℃)0.8682.644×10-3

2.1.1 水浸温度与平衡吸湿率的关系

图2为平衡吸湿率和水浸温度的关系曲线。从实验所得结果可以看出水浸温度越高，平衡吸湿率越大。水浸温度与平衡吸湿率呈正相关。

拟合图2中曲线所得方程为：

M∞=0.00679+(9.6027×10-8)e0.028T

(其中T:333.15～373.15K)

(6)

式中：T表示绝对温度(K)。

由式(6)可以预测此复合材料在60～100℃内任意水浸温度下的平衡吸湿率。

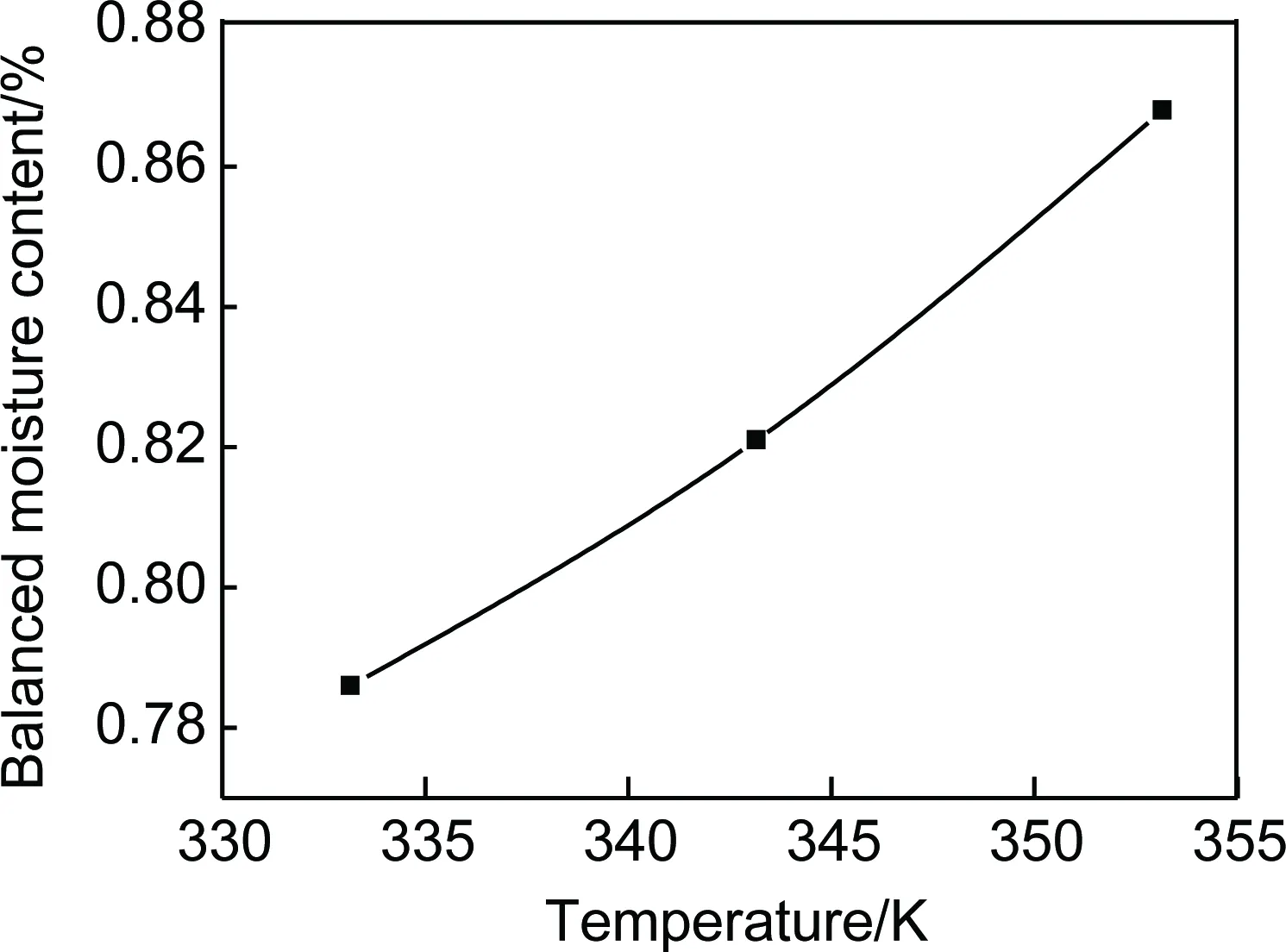
图2 复合材料的平衡吸湿率与温度的关系

2.1.2 水浸温度与扩散系数的关系

许多与温度有关的物理和化学过程中存在着Arrhenius关系[16]。纤维增强树脂基复合材料吸湿的初期阶段是较为单纯的物理过程。水在复合材料中的扩散可以看成是一个热活化能的过程[17]。这样就可以用Arrhenius方程描述复合材料初始阶段的水扩散系数D与温度T之间的关系，其规律表示为：

(7)

式中：A为Arrhenius常数(mm2/h)；E为吸湿活化能(kJ/mol)；R为气体常数(kJ/mol·K)。

将(7)式两边取对数得：

(8)

可以发现，lnD和(1/T)呈线性关系，将不同水浸温度下的吸湿扩散系数值代入(8)式，用单对数坐标画出扩散系数D与绝对温度T的倒数1/T的关系，进行一元线性回归，直线的斜率和截距分别为-E/R和lnA，从而求得E/R和A。图3为lnD对1/T的关系曲线。线性拟合所得的回归方程为：

lnD=4.23037-3591.86514(1/T)

(9)

从而：E/R=3591.86514，lnA=4.23037。故：

(10)

图3 复合材料的扩散系数lnD与温度1/T的关系

根据式(10)就可预测任意水浸温度下该复合材料的水扩散系数。

2.1.3 吸湿计算模型的建立

将式(6)和式(10)代入式(4)得：

(11)

运用计算模型(11)就可求出该复合材料在60～100℃内任意水浸温度下线性吸湿阶段任意时刻的吸湿量，也可预估在某水浸温度下达到线性吸湿阶段某个特定吸湿量所需要的时间。

由于一维Fickian理论不适用于吸湿后期，所以计算模型(11)只能预测线性吸湿阶段的吸湿量，为了预测整个吸湿过程，运用吸湿率Mt与时间t的另一个通式关系[18]：

(12)

将式(6)和式(10)代入式(12)得：

(13)

运用计算模型(13)就可以求得该复合材料在60～100℃内任意水浸温度下任意时刻的吸湿量，也可预估在某水浸温度下该复合材料达到特定吸湿量所需要的时间。

2.2 吸湿动力学计算模型的验证

为了验证所建吸湿动力学计算模型(11)的准确性，在95℃恒温水浸下，选择线性吸湿阶段的多个吸湿时刻t，运用计算模型(11)计算出各个时刻的吸湿率，并进行吸湿实验测量这些时刻的吸湿率。将复合材料计算结果与实验所得结果进行比较，如图4所示。

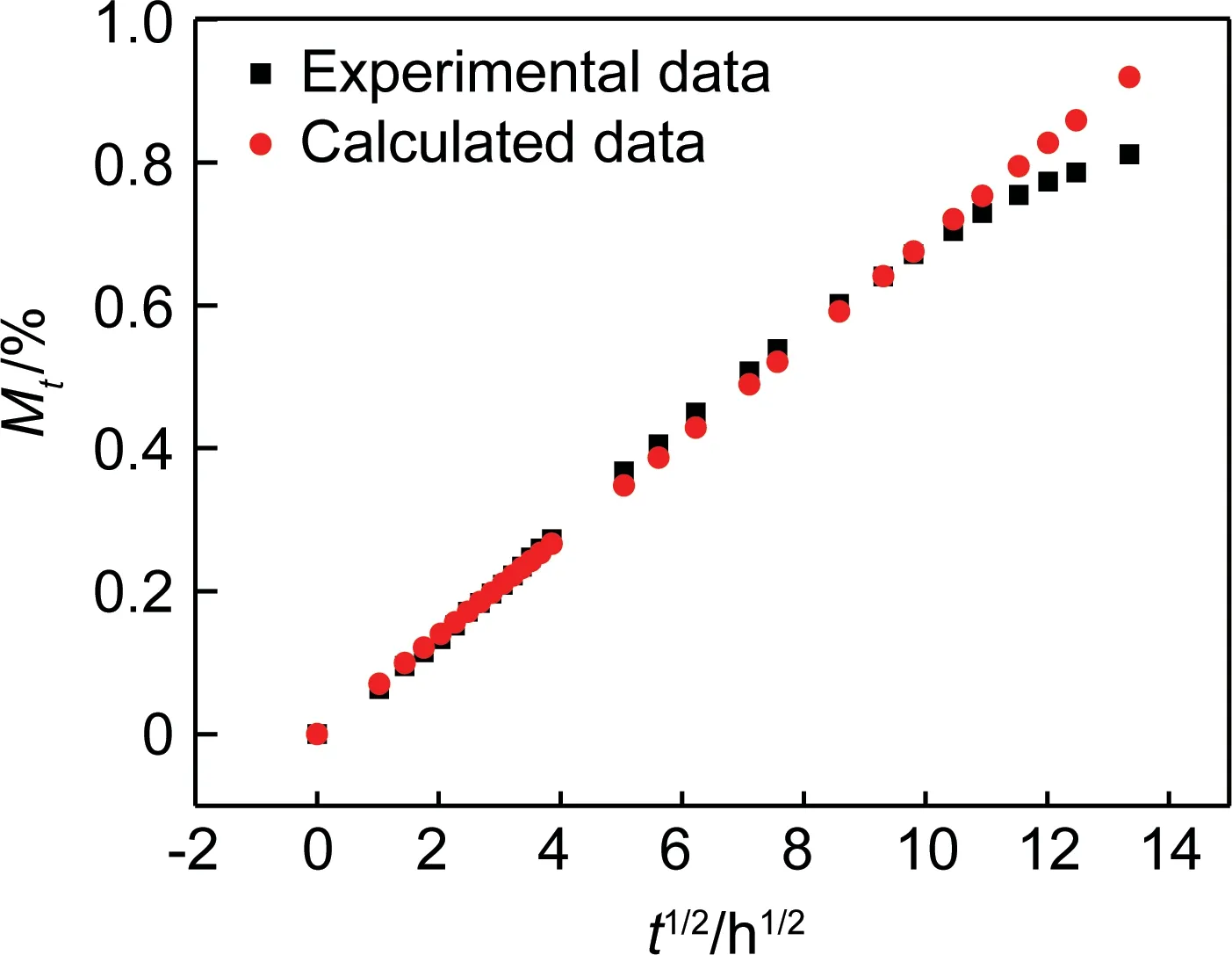
图4 95℃水浸条件下初始阶段吸湿率的实验结果与计算结果比较

从图4中可以看出，在吸湿初期即线性吸湿阶段，吸湿模型计算值与实验值吻合的较好，偏差很小，而在吸湿后期出现了较大偏差，这种偏差随着吸湿的进行逐渐变大。在吸湿初期，复合材料吸湿主要是由于材料本身缺陷和树脂吸水造成的，在温湿度的共同作用下，水分较快地通过空隙和裂纹进入材料内部。随着吸湿时间的进一步增加，吸水速率明显减慢。由于吸湿计算模型(11)是以Fick第二定律为基础推导得来，在吸湿初期，复合材料的吸湿过程服从一维Fickian理论，但当水浸时间较长后，吸湿量与时间的平方根不再成正比，此时材料的吸湿行为已难以用一维Fickian理论表征[19]，所以计算模型(11)失效，产生较大偏差。

另外，在线性吸湿阶段实验值与模型计算值也存在着微小的偏差，偏差产生的原因主要有以下几个方面：(1)此复合材料的平衡吸湿率和扩散系数均依据实验数据所得，实验数据存在测量误差，所以导致这两个吸湿参数存在一定误差；(2)吸湿实验数据比较分散，本身就存在测量误差，因此不可避免地导致实验数据和模型计算结果不能完全吻合；(3)该吸湿计算模型忽略了试样的侧面吸湿，因此可能导致线性吸湿阶段实验值比计算值略微偏大。(4)在吸湿计算模型建立的过程中也存在着微小的计算误差。

为了验证吸湿动力学计算模型(13)的准确性，将95℃恒温水浸下该复合材料吸湿率的计算结果与实验所得结果进行比较。如图5所示。

图5 95℃水浸条件下吸湿率的实验结果与计算结果比较

从图5中可以看出模型计算值与实验值在吸湿前期和吸湿趋于饱和这两个阶段基本吻合，在吸湿中期某些时刻存在一定的偏差，不过相差不是很大，也基本能符合吸湿量的变化规律，造成这种现象的原因主要有：(1)所建立的吸湿计算模型忽略了试样的侧面吸湿，这可能是吸湿前期实验值比计算值略微偏大的原因；(2)在试样质量的测量过程中存在着一定的测量误差；(3)在计算过程中也不可避免地存在微小的计算误差。

3 结论

(1)此复合材料吸湿初始阶段符合Arrhenius关系和Fick定律，Fick第二定律只适用于线性吸湿阶段，在吸湿后期，材料的吸湿行为难以用一维Fickian理论表征。

(2)水浸温度对扩散系数和平衡吸湿率都有影响。水浸温度越高，吸湿越快，扩散系数值越大，平衡吸湿率也越大。

(3)根据Arrhenius公式可以方便地预测任意水浸温度下纤维增强树脂基复合材料的水扩散系数，再结合Fick定律可预测任意水浸温度下纤维增强树脂基复合材料任意时刻的吸湿率。

(4)所建吸湿模型能较好地预测此复合材料在95℃水浸温度下的吸湿规律。

[1] 杜善义.先进复合材料与航空航天[J].复合材料学报,2007,24(1):1-12.

DU S Y. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007,24(1):1-12.

[2] 沈军,谢怀勤.先进复合材料在航空航天领域的研发与应用[J].材料科学与工艺,2008,16(5): 737-740.

SHEN J, XIE H Q. Development of research and application of the advanced composite materials in the aerospace engineering[J].Materials Science and Technology, 2008,16(5): 737-740.

[3] KUMAR S B, SRIDHAR I, SIVASHANKER S. Influence of humid environment on the performance of high strength structural carbon fiber composites[J].Materials Science and Engineering: A,2008, 498(1):174-178.

[4] 孙博,李岩.复合材料湿热老化行为研究及其耐久性预测[J].玻璃钢/复合材料,2013,(4):28-34.

SUN B, LI Y. The study on hygrothermal aging behavior of composites and the prediction model of durability[J]. Fiber Reinforced Plastics/Composites, 2013,(4):28-34.

[5] 谢可勇,李晖,孙岩,等.湿热老化对纤维增强树脂基复合材料性能的影响及其机理[J].机械工程材料,2014,38(8):1-5.

XIE K Y, LI H, SUN Y, et al. Effect of hygrothermal aging on behaviors of fiber reinforced resin composites and its mechanism[J]. Materials for Mechanical Engineering, 2014,38(8):1-5.

[6] 曹东, 张晓云, 陆峰, 等. 先进复合材料T300/5405综合环境实验谱的研究[J]. 材料工程, 2014, (7): 73-78.

CAO D, ZHANG X Y, LU F,et al. Synthetical environmental spectrum aging of T300/5405 advanced composite material[J]. Journal of Materials Engineering, 2014, (7): 73-78.

[7] WAN Y Z,WANG Y L,HUANG Y, et al. Hygrothermal aging behaviour of VARTMed three-dimensional braided carbon-epoxy composites under external stresses[J].Composites Part A,2005, 36(8):1102-1109.

[8] MERCIER J, BUNSELL A, CASTAING P ,et al. Characterisation and modelling of aging of composites[J].Composites Part A,2008,39(2):428-438.

[9] 黄超,陶春虎,王占彬,等.T300/648复合材料湿热老化行为与贮存寿命预测[J].四川兵工学报, 2013,34(11):137-140.

HUANG C, TAO C H, WANG Z B, et al. T300 /648 composite material hygrothermal ageing behaviour and life prediction of storage[J]. Journal of Sichuan Ordnance, 2013,34(11): 137-140.

[10] AKBAR S, ZHANG T. Moisture diffusion in carbon/epoxy composite and the effect of cyclic hydrothermal fluctuations: characterization by dynamic mechanical analysis (DMA) and interlaminar shear strength (ILSS) [J].Adhesion, 2008, 84(7): 585-600.

[11] BAO L R, YEE L F, LEE C Y. Moisture absorption and hygrothermal aging in a bismaleimide resin[J]. Original Research Article Polymer, 2001, 42(17): 7327-7333.

[12] WAN Y Z, WANG Y L, LUO H L, et al. Moisture absorption behavior of C3D/EP composite and effect of external stress [J]. Materials Science and Engineering:A, 2002, 326(2): 324-329.

[13] 李静.纤维增强树脂基复合材料的吸湿性和湿变形[J].航天返回与遥感,2010,31(2):69-74.

LI J. Moisture absorption and soaking deformation of fiber reinforced resin composites[J]. Spacecraft Recovery & Remote Sensing, 2010,31(2):69-74.

[14] 曹素,王波,矫桂琼.T700/9916复合材料层合板恒温吸湿行为研究[J].航空材料学报,2012,32(2): 59-64.

CAO S, WANG B, JIAO G Q. Research on water-sorption behaviors of T700 /9916 composite laminates[J]. Journal of Aeronautical Materials, 2012,32(2): 59-64.

[15] 谢可勇,李晖,孙岩,等.纤维增强树脂基复合材料吸湿特性实验方法[J].合成材料老化与应用，2013,42(4):30-33.

XIE K Y, LI H, SUN Y, et al. The method of study of moisture absorption on fiber reinforced resin composites[J]. Synthetic Materials Aging and Application, 2013,42(4):30-33.

[17] 郑路,常新龙,赵峰,等.湿热环境中复合材料吸湿性研究[J].纤维复合材料,2007,(2):37-39.

ZHENG L, CHANG X L, ZHAO F, et al. Research on moisture absorption of composites in the hydrothermal environment[J]. Fiber Composites, 2007,(2):37-39.

[18] 陈新文,许凤和.T300/5405复合材料的吸水特性研究[J].材料工程,1999,(5):6-8.

CHEN X W, XU F H. Study of absorption characteristics of T300/5405 composites[J]. Journal of Materials Engineering, 1999,(5):6-8.

[19] 回丽,许磊,许良,等.碳纤维增强环氧复合材料吸湿行为研究[J].化工新型材料,2014,42(7):90-92.

HUI L, XU L, XU L, et al. Research on water-sorption behavior of carbon fiber reinforced epoxy composite laminates[J]. New Chemical Materials, 2014,42(7):90-92.

[20] 过梅丽,肇研,谢令.航空航天结构复合材料湿热老化机理的研究[J].宇航材料工艺,2002,(4):51-54.

GUO M L, ZHAO Y, XIE L. Study on hygrothermal ageing mechanisms of aerospace structural composites[J]. Aerospace Materials & Technology, 2002,(4):51-54.

--------------------●

Moisture Absorption Model of Composites Considering Water Temperature Effect

HUI Li1,2，WANG Yong-gang1，XU Liang1，MA Shao-hua1，ZHANG Xu1，FEI Bing-qiang1

(1 School of Mechatronics Engineering，Shenyang Aerospace University，Shenyang 110136，China；2 Key Laboratory of Fundamental Science for National Defense of Aeronautical Digital Manufacturing Process，Shenyang Aerospace University，Shenyang 110136，China)

The influence of water temperature on composite moisture absorption parameters was investigated in temperature-controlled water bath. Experiments of carbon fiber/bismaleimide resin composites immersed in water of 60℃, 70℃and 80℃ were developed respectively. According to the moisture content-time curves obtained from the experimental results, the diffusion coefficient and the balanced moisture content of the composites immersed in different water temperature could be calculated. What’s more, the effect of water temperature on the diffusion coefficient and the balanced moisture content were discussed too. According to the Arrhenius equation and the law of Fick, a moisture absorption model was proposed to simulate the hygroscopic behaviour of the composite laminates immersed in different water temperature which can predict the absorption rate of water of the composites immersed in distilled water of 95℃ at any time precisely and can calculate how long it will take to reach the specific absorption rate.

composite；Arrhenius equation；the law of Fick；moisture absorption model

10.11868/j.issn.1001-4381.2016.11.014

TB332

A

1001-4381(2016)11-0083-05

航空科学基金资助项目(2013ZA54012)

2015-10-25；

2016-07-30

许良(1965-)，男，副教授，主要从事复合材料和金属材料性能研究，联系地址：辽宁省沈阳市道义南大街37号沈阳航空航天大学机电工程学院(110136)，E-mail: sysyxu@163.com