HBP立体匹配算法性能分析与仿真实验

王 鹏，朱 姝，胡古月，杨容浩,2

（1.成都理工大学，四川 成都 610059；2.四川省应急测绘与防灾减灾工程技术研究中心，四川 成都 610041）

HBP立体匹配算法性能分析与仿真实验

王 鹏1，朱 姝1，胡古月1，杨容浩1,2

（1.成都理工大学，四川 成都 610059；2.四川省应急测绘与防灾减灾工程技术研究中心，四川 成都 610041）

多层次置信度传播（HBP）立体匹配算法是传统置信度传播算法通过距离变换优化、奇偶场优化、金字塔优化算法改进后的高性能算法。介绍了HBP算法的原理及相关理论模型，分析了HBP算法的参数多且设置困难、实用性不高等问题。运用穷举最佳组合的方式求取了3组图像的最佳组合参数，发现不同数据的最佳组合参数不一致，并对参数设置规律进行了分析总结。

立体匹配；置信度传播；马尔科夫随机场；吉布斯分布

立体匹配不仅是计算机视觉领域中的研究热点与难点，还是约束立体视觉发展的重要组成部分[1]。当真实场景中的物体被投影到二维平面上的时候，包含了真实场景的形状、特征、亮度等多种信息，并通过像素灰度值来表示。但是由于投影过程中仪器自身的缺陷，如畸变、角度、光线的影响造成了图像匹配错误，使立体匹配成为了一个典型的病态问题[2]。立体匹配难点有遮挡、光照变化、弱纹理和纹理区域的误匹配等。

本世纪初，立体匹配的研究热点已从局部优化问题转到全局最优化问题，即构建全局能量函数不仅需要局部最优，还要对局部最优问题进行全局约束，从而提高立体匹配的精度[3]。这样全局优化问题就转到能量函数的构建以及如何让能量函数最小最优的问题上来。基于马尔科夫随机场理论的HBP立体匹配算法是目前解决这一问题很有效的方案[4]。

1 HBP算法基本原理

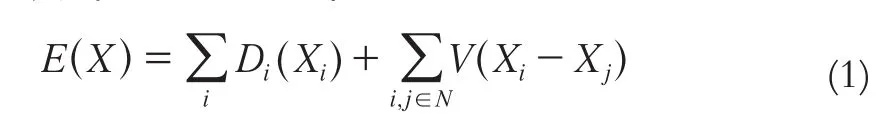
立体匹配算法就是解决全局能量最小化的问题[5]，定义全局能量函数的公式为：式中，X表示图像在像素点i处可能的视差值；N表示图像中所有像素的四邻域像素点集；Xi表示i点所分配的视差值；不连续代价V（Xi-Xj）表示两相邻像素点i和j分配视差Xi和Xj时视差不连续代价集合；数据项Di（Xi）表示像素点i在视差为Xi时的相似度。

HBP算法的理论基础是马尔科夫随机场，其数学定义如下：假设随机场X是定义在邻域系统N上的马尔科夫随机场，并满足以下2个条件：

条件二中的概率称为马尔科夫随机场的局部特征，所有能满足条件一的概率都通过条件二来进行唯一性约束[6]。在实际应用中，要确定这2个条件概率是一件很困难的事情。20世纪80年代，Hammersley Clifford验证了马尔科夫随机场与吉布斯分布的等价关系[7-9]，并使用吉布斯分布来求解马尔科夫随机场中的概率分布。吉布斯分布一般定义形式为：

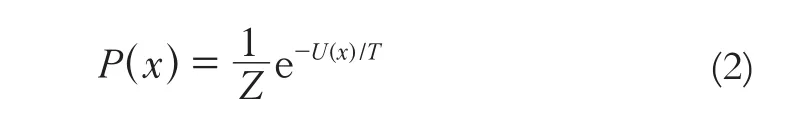
式中，Z 表示归一化参数；U（x）表示能量函数；T表示一个温度常数。

HBP算法的2个关键是：①通过加权乘积计算所有的局部消息；②节点之间概率消息在随机场中的传递[10]。首先将整个节点空间进行分层处理，这样就可以使远距离的像素间相互作用在粗图像中通过短路径获取。令L0=L，L表示节点空间。Lk表示第k层的节点空间。在整个金字塔模型中，上一层的每个节点都可以向下映射到下一层的2×2个节点，因此，第k层的每一个节点就可以映射到L0上的ε×ε（ε=2k）个节点，如图1所示。

将节点空间进行分层以后，就要在每一层的节点间进行消息的传递，因此，定义消息传递函数：

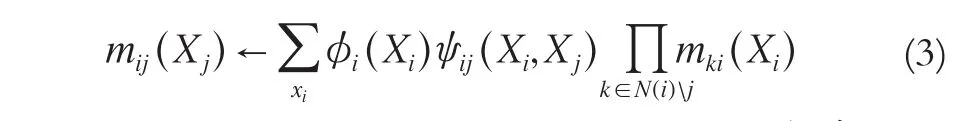
为了将立体匹配能量与置信度传播联系起来，定义以下变换：

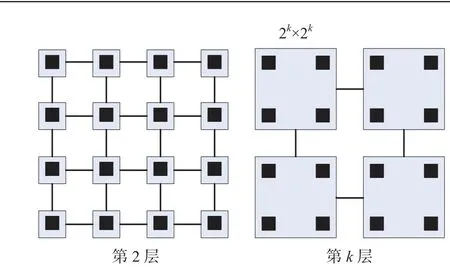
图1 金字塔模型

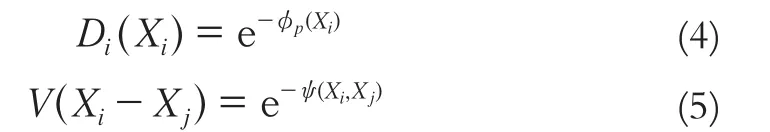
经过变换有：

令：

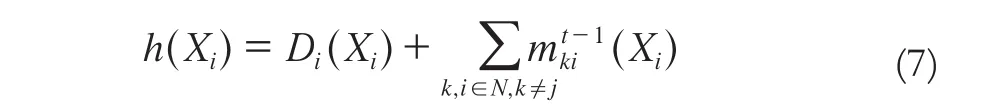
则消息函数可以改写为：

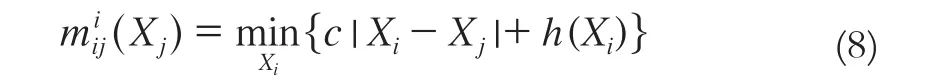
将标签量化，然后将量化后的每一级标签对应到相应的标记网格中。式（8）可以看作是k个倾斜45°的三角锥，在网格中的每一个Xi都能对应一个在（Xi，h（Xi））上的三角锥[10]。然后通过向前向后算法进行距离变换，对更新的消息进行计算。向前向后处理算法为：

1）初始化：m（Xj）=h（Xj）

2）向前处理：for Xjfrom 1 to k-1

m（Xj）←min（m（Xj），m（Xj，m（Xj-1）+c）

3）向后处理：for Xjfrom k-2 to 0

m（Xj）←min（m（Xj），m（Xj,m（Xj+1）+c）

多层次置信度传播立体匹配算法主要研究基于四邻域系统的图像模型，如果着色网格图形为棋盘图案，每边连接不同颜色的节点，此时的网格图就是二分图，如图2所示（图中黑色方格为A，白色方格为B，这样二分图可以表示为A∪B）。用表示在第t次迭代时，节点i向节点j传递的消息。当t为奇数，只对A节点中的消息进行更新而不改变B节点中的消息。当t为偶数恰好相反，保持A节点中的消息而更新B节点中的消息。

图2 二分图

T次迭代以后可以计算每一个节点的置信度向量。

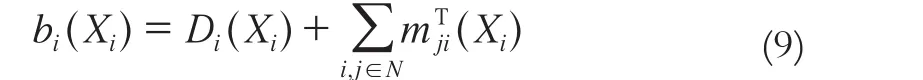
然后通过计算置信度最小时对应的标签值，得到该节点的最佳视差值：

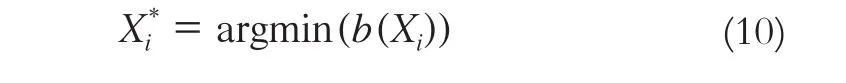
2 算法仿真实验

HBP算法的难点是需要设置的参数很多，而且没有规律可循。此节分析了不同参数影响算法结果的变化趋势。本次实验测试的参数包括迭代次数T、数据项阀值K1、不连续代价阀值K2、数据项权重系数λ。每次实验固定其中3个参数，变化1个参数，然后通过穷举最优组合的方法得到每一组图像的最优参数组合。

2.1 精度评定

本次实验数据来自美国Middle学院的立体匹配公共测试平台数据库中名为Tsukuba、Vensus、Teddy的3幅图片。对于立体匹配算法精度的评价标准有均方根误差和误匹配率。

均方根误差：

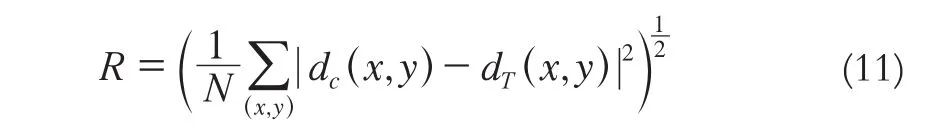
误匹配率：

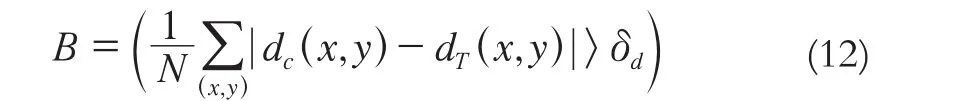
两式中，N表示图像中的像素总数；dc表示计算得到的视差值；dT是标准视差值；δd表示允许误差阀值，一般取值为1。实验数据各参数参考值如表1。

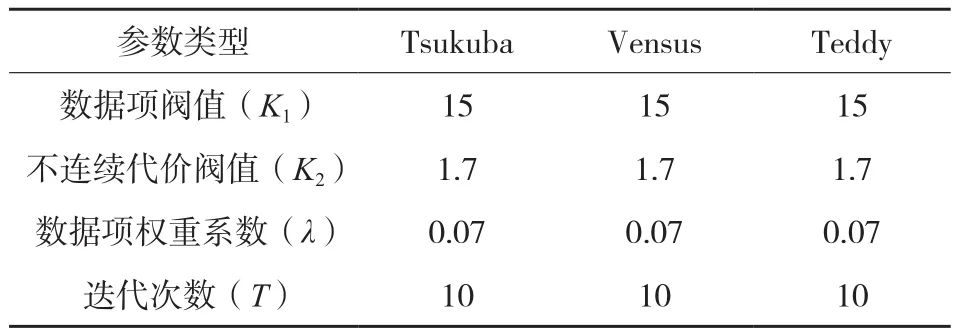
表1 3组图片的4种参数的参考值

2.2 实验结果分析

分别以数据项权重系数为例，固定其他3个变量预设参数值，得到关于数据项权重系数变化情况下的均方根误差变化趋势图（图3）。

从图3可以看出，3幅图片的最佳权重系数分别为0.06、0.06、0.02。重复以上计算，可以得到单个参数最佳值表。然后以第一组为参考值进行第二轮参数设置，得到第二轮测试的最佳参数值。通过反复实验，最终得到3组图片最佳组合参数，见表2。

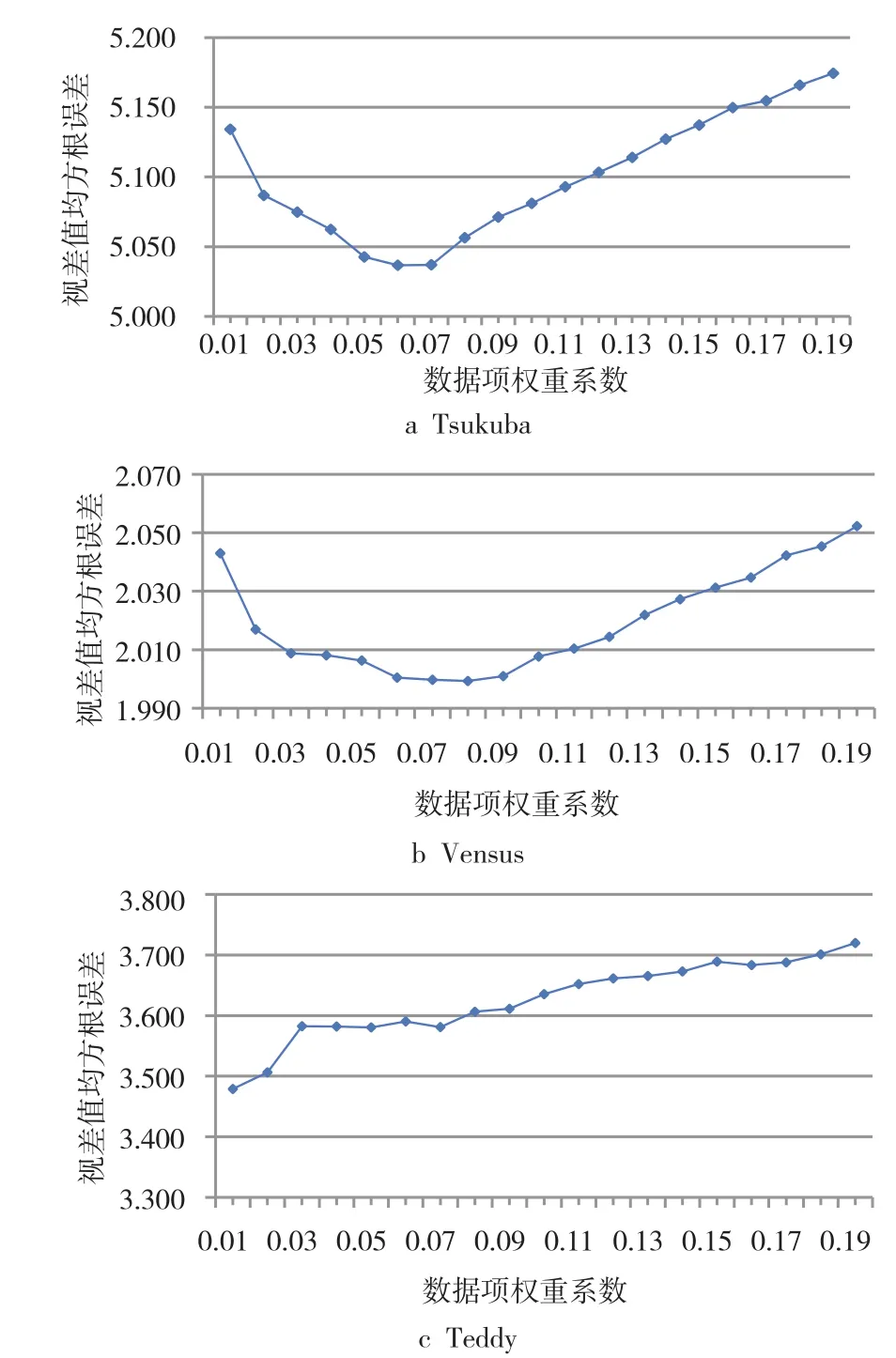
图3 权重系数λ均方根误差变化趋势图

表2 实验结果

3 结 语

通过实验分析了HBP算法中各项参数对精度的影响，得到的结论是：①算法基本在3～5次迭代后就能达到收敛值。②在数据项权重系数、数据项阀值、不连续代价阀值3个参数中，数据项权重系数的影响最大，参数的设置在很大程度上与原始图像亮度相关，对于整体亮度较低或者局部亮度较低的图像，数据项权重系数较小，反之较大。③数据项阀值、不连续代价阀值与亮度和场景复杂度有关，但影响因素要小于数据项权重系数。④HBP算法通过消息迭代更新进行视差优化，对于场景中的错误信息同样会进行传播，特别是低纹理或者无纹理区域，这也是HBP算法的局限性。

[1] 游素亚.立体视觉研究的现状与进展[J].中国图像图形学报,1997(1)：17-24

[2] 石春琴.随机光照双目立体测量系统中的若干关键问题研究[D].南京：南京航空航天大学,2011

[3] 宋长波.基于线特征的立体视觉匹配研究[D].武汉：武汉大学,2004

[4] 陈侃.基于马尔科夫随机场图像恢复算法研究[D].南京：南京师范大学,2008

[5] 赵笑可.基于全局能量最小化的立体匹配算法研究[D].南京：南京理工大学,2008

[6] 李旭超,朱善安.图像分割中的马尔可夫随机场方法综述[J].中国图像图形学报,2007(5)：789-798

[7] Besag J.Spatial Interaction and the Statistical Analysis of Lattice Systems[J]. J.R.Statist.Soc.B,1974,36(2)：192-236

[8] 万成凯.无标记人体运动捕捉及姿态估计的研究[D].北京：北京交通大学,2009

[9] Moussouris J.Gibbs and Markov Random Systems with Constraints[J].Journal of Statistical Physics,1974,10(1)：11-33

[10] 饶旻骅.基于置信度传播的立体匹配算法研究[D].武汉：华中科技大学,2010

P237

B

1672-4623（2016）08-0020-03

10.3969/j.issn.1672-4623.2016.08.007

王鹏，硕士研究生，研究方向为摄影测量与计机视觉。

2015-12-01。

项目来源：国家级大学生创新创业训练计划资助项目（201410616005）；四川省应急测绘与防灾减灾工程技术研究中心开放基金资助项目（K2014B001）；四川省教育厅科研资助项目（15ZA0060）。