引入联跳的中国股市协方差预测——基于多元HAR模型

瞿 慧，纪 萍

南京大学 工程管理学院，南京 210093

引入联跳的中国股市协方差预测
——基于多元HAR模型

瞿 慧，纪 萍

南京大学 工程管理学院，南京 210093

金融资产的时变协方差矩阵是投资组合配置、风险管理等实务活动的关键参数。早期的协方差预测模型研究使用日数据或者更低频数据，但大多存在参数估计困难和维数灾难等问题。

运用日内高频数据可以构建协方差矩阵的后验非参数估计量，使其从隐变量转变为可以直接建模的可观测变量，降低协方差模型估计的复杂性并增强模型的高维适用性。进一步的，利用高频数据还可以识别多个金融资产的价格在日内同一采样间隔内发生的跳跃，即多资产联跳。针对联跳多由宏观经济新闻公告和政策制度等的发布引起，这些信息终将被吸收并体现在协方差矩阵中，联跳可能蕴含着对协方差预测有益的信息，因此识别联跳并将其引入协方差预测模型。

将异质自回归模型扩展至多元形式，作为协方差非参数估计量的基准模型，并将取值0/1的联跳指示变量与Hawkes模型估计出的联跳强度分别及同时引入多元形式模型，构建3种扩展模型。选择均方误差和平均绝对误差这两种常用统计意义损失函数，采用Diebold Mariano检验，评价各扩展模型的样本外预测性能相对于基准模型是否有所改进，并采用模型置信集检验并挑选最佳扩展模型。此外，比较各种预测模型用于全局最小方差投资组合策略的效果。

基于上证50指数成分股中不同行业5只高流动性个股分钟高频价格数据进行实证，研究结果表明，①相对于联跳指示变量，联跳强度对协方差矩阵的预测有更显著的贡献；②引入联跳强度可以显著提升对协方差的拟合优度和样本外预测精度；③同时引入联跳强度和联跳指示变量，且采用矩阵对数变换，确保正定性的扩展多元形式模型在统计和经济意义上都是最优模型。

研究结论肯定了在协方差预测模型中引入联跳的重要价值，并揭示了宏观信息对协方差预测的贡献，对于金融管理者和投资者进行金融风险管理及进行资产配置都具有实际指导意义。

协方差预测；联跳；多元异质自回归模型；Hawkes模型；模型置信集检验；全局最小方差投资组合

1 引言

随着股指期货正式上市交易、融资融券成为常规业务等一系列创新性举措的实施，中国资本市场向着多层次资本市场体系的方向不断迈进，给投资组合配置、风险管理等带来了更大的机会和挑战，而金融资产的时变协方差矩阵则是这些实务应用的决定性参数，对其精准的建模预测具有重要意义。早期研究多使用日数据或者更低频数据，主要在多元GARCH类模型或者多元随机波动率模型框架下研究多资产收益向量的条件协方差矩阵，但大多存在估计困难和维数灾难等问题。

近10年来，日内高频数据的可得性为多资产协方差矩阵的估计、建模和预测提供了新的手段。利用高频数据可以构建协方差矩阵的后验非参数估计量，使其从隐变量转变为可以直接建模的可观测变量，一定程度上降低了模型参数估计的复杂性，并使预测高维协方差矩阵成为可能。进一步的，利用高频数据还可以识别多个金融资产的价格在日内同一采样间隔内发生的跳跃，即多资产联跳。跨行业的多资产联跳通常由宏观经济新闻公告和政策制度等的发布引起，这些信息终将被整个市场消化并体现在协方差矩阵中。因此，本研究认为联跳可能蕴含着对预测协方差有益的信息，识别联跳并探索将其引入协方差模型的合理形式具有重要指导意义。

2 相关研究评述

ANDERSEN et al.[1]实证得出日内对数收益率平方和计算的已实现波动率是对日波动的精确测度；BARNDORFF-NIELSEN et al.[2]对已实现波动率进行多元拓展，提出已实现协方差(realized covariance,RCov)。鉴于RCov包含连续扩散性分量(即积分协方差)以及各资产跳跃和多资产联跳的共同影响，他们还构建了跳跃(联跳)稳健的已实现双幂次协变差(realized bipower covariation, RBPCov)[3]，对积分协方差进行估计。RCov和RBPCov都属于协方差已实现估计量，实际运用中，协方差已实现估计量的构建还需考虑市场微观结构噪声的影响和非同步交易在采样频率较高时引起的估计量零偏(Epps效应)，除了合理降低采样频率外[2-3]，学者们还提出双尺度已实现协方差[4]、多元已实现核[5]、流动性分块双尺度已实现协方差[6]等改进的协方差已实现估计量[7]。已实现协方差及其各种改进估计量的建模除了需要刻画波动和相关结构的长记忆性外，还需要确保预测矩阵的正定性。BAUER et al.[8]提出的矩阵对数变换方法和CHIRIAC et al.[9]提出的Cholesky分解法，都可以使重构出的预测协方差矩阵确保正定。而在预测模型的选择方面，鉴于异质自回归模型(heterogeneous autoregressive,HAR)[10]具有较优的数据刻画和预测能力，而且可以采用简便的OLS估计，不少学者将其拓展至多元应用[9,11-12]。在针对中国市场的研究中，韩立岩等[13]和WANG et al.[14]为沪深300指数和股指期货的协方差建模时、唐勇等[15]为上证综指和深证成指协方差建模时都以多元HAR模型作为基础模型。中国针对多(>2)资产协方差已实现估计量的建模研究还比较少，刘丽萍[16]对沪深300指数不同行业6只大盘股的实证研究表明，采用矩阵对数变换方法结合多元HAR模型在7种损失函数下都可以获得最优的预测能力，且显著超越使用日数据的DCC和BEKK模型；刘丽萍等[17]采用不同行业12只股票的实证研究也发现，该模型在统计和经济意义下都较优。

高频数据的可得使对多个金融资产价格同步跳跃的识别成为可能。针对多(>2)资产的联跳识别主要有两类方法。一类是BOLLERSLEV et al.[18]基于投资组合理论构建平均外积(mean cross product, MCP)统计量，简称BLT方法；另一类是LAHAYE et al.[19]和GILDER et al.[20]在单资产日内跳跃识别基础上提出的同步发生准则。学者们运用上述联跳识别方法分析联跳与多种宏观经济新闻公告之间的联系[19-21]。鉴于联跳蕴含的这些信息将被市场吸收并体现在协方差矩阵中，部分学者开始探索将其引入协方差预测模型。WANG et al.[14]在沪深300指数和股指期货的二元HAR模型中引入基于同步发生准则计算的跳跃协变差(文中作为联跳的度量)，明显提高了协方差模型的调整R2。CLEMENTS et al.[22]在用BLT方法识别道琼斯指数成分股联跳后，利用Hawkes模型[23]估计出联跳强度，并实证指出将其引入指数已实现波动率的HAR模型可以显著改善其预测精度。

到目前为止，尚未有研究考虑在多(>2)资产的协方差已实现估计量预测模型中引入联跳。由于选择不同行业的多只股票并配以合理的权重以分散风险已成为投资者们广泛使用的股市操作，研究如何引入联跳以寻求此类中、高维度协方差矩阵预测性能的改进具有重要的实践指导意义。鉴于此，本研究以上证50指数成分股中不同行业5只个股的日内高频价格为实证数据，以多元HAR模型作为协方差已实现估计量的基准模型，并分别及同时引入取值为0/1的联跳指示变量和Hawkes模型估计的联跳强度，以构建扩展模型。一方面与已有引入联跳的研究[14,22]一样，使用统计意义指标直接计算协方差预测精度，采用Diebold Mariano(DM)检验[24]，评价各扩展模型相对于基准模型的样本外预测性能是否有所改进，并采用模型置信集(model confidence set, MCS)检验[25]挑选最佳模型。另一方面，提出从应用的角度间接评价，比较基于各种模型预测构建全局最小方差投资组合的绩效。最后，对在协方差已实现估计量预测模型中引入联跳的意义和引入联跳的合理方式作出结论，以期为投资者的实务运用提供有效基础性工具。

3 模型和方法

3.1 已实现估计量的构建

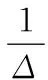
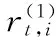
3.2 联跳识别

运用BLT方法[18]识别多资产联跳，并在构建MCP统计量时运用BOUDT et al.[27]的赋权标准偏差(weighted standard deviation,WSD)因子，对日内收益模式进行调整。

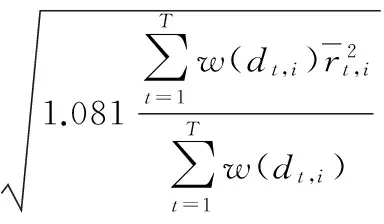
(1)

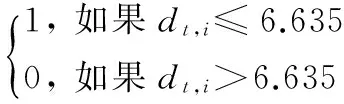
采用日内收益模式调整的BLT方法构造MCP统计量，即

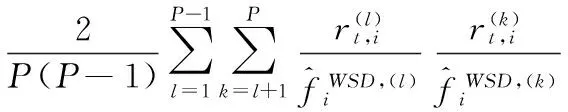
i=1,2,…,M

(2)

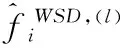
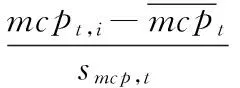
(3)

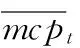
由于实证结果显示Zmcp,t,i统计量不近似服从于任何标准分布，因此采用bootstrap的方法估计其经验分布。令Fα为Zmcp,t,i统计量的分布函数在置信度为α时的临界值，则联跳存在性识别为CJt，CJt=I(Zmcp,t,i>Fα)，这里的I(·)为取值0或1的指示函数。

3.3 联跳强度的Hawkes模型

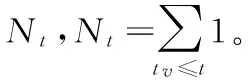
(4)

其中，μ为常数，μ>0；ω(·)为非负权重函数，常用指数函数表示，ω(t)=αe-βt，此时有

(5)

其中，α为联跳发生对强度的瞬时影响的参数，β为控制指数权重函数衰减速率的参数，有约束α>0，β>0。

相应的，可以计算对数似然函数并进行极大似然估计，即

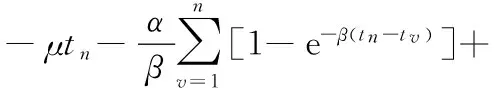
(6)

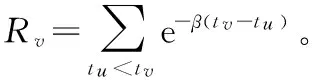
3.4 多元HAR模型及其扩展

为了确保预测协方差矩阵的正定性，先对协方差已实现估计量Σt进行矩阵对数变换[8]或者Cholesky分解[9]，为变换后的序列构建(扩展的)多元HAR模型进行预测后，再重构协方差矩阵。

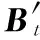
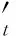
以多元HAR(即MHAR)模型作为基准模型，具体形式为

(7)

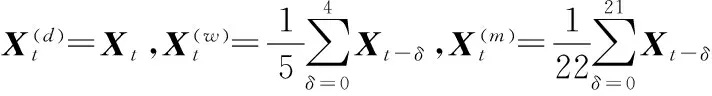
将取值0或1的联跳指示变量CJt作为解释变量加入到MHAR模型中，将其扩展为MHAR-CJ模型(LOG-MHAR-CJ模型或CF-MHAR-CJ模型)，用参数γ度量联跳对未来估计量的贡献，即

(8)

将估计出的联跳强度λt作为解释变量加入到MHAR模型中，将其扩展为MHAR-CI模型(LOG-MHAR-CI模型或CF-MHAR-CI模型)，用参数η度量联跳强度对未来估计量的贡献，即

(9)

这里的联跳强度解释变量下标为(t+1)，因为λt包含的仅是截止到(t-1)日的历史联跳信息。

此外，也考虑在MHAR模型中同时引入联跳指示变量和联跳强度的情况，将其扩展为MHAR-CJI模型(LOG-MHAR-CJI模型或CF-MHAR-CJI模型)，即

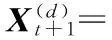
(10)

3.5 协方差预测模型性能比较

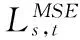
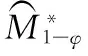
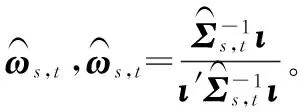
4 实证分析

4.1 数据描述

将已实现双幂次协变差作为协方差已实现估计量Σt，为确保预测协方差矩阵的正定性，先分别对Σt进行矩阵对数变换和Cholesky分解。表1给出总样本区间内对数矩阵At上三角各元素的描述性统计，表2给出总样本区间内Cholesky分解上三角阵Γt各元素的描述性统计，JB为Jarque-Bera统计量的p值，大于0.100的已标为黑体，表示无法拒绝正态分布原假设；LB(10)为滞后10阶的Ljung-Box Q统计量的p值，大于0.100的已标为黑体，表示无法拒绝10阶不相关原假设；ADF为Augmented Dickey-Fuller单位根检验的p值。

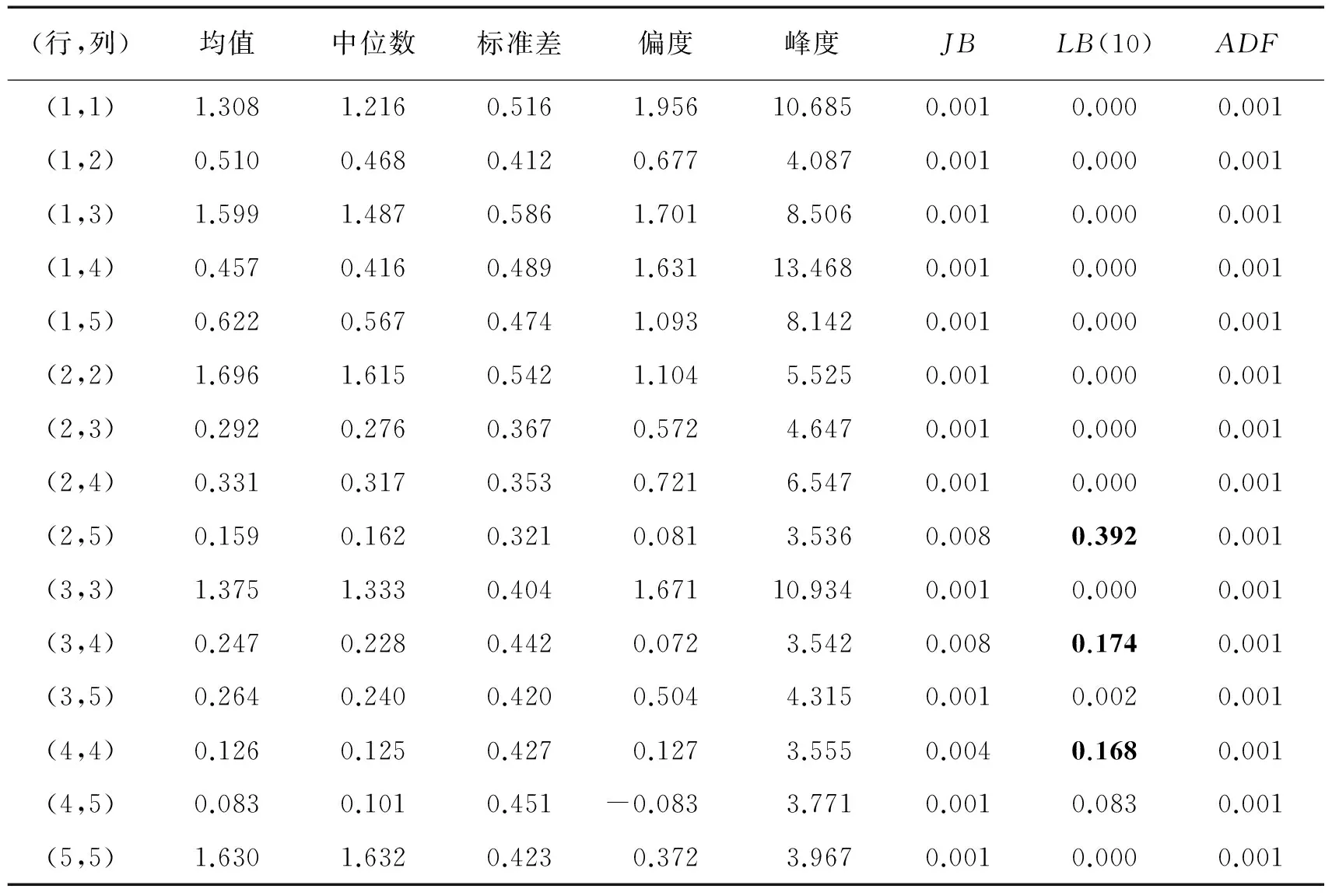
表2 已实现双幂次协变差矩阵的Cholesky分解上三角阵Γt各元素的描述性统计Table 2 Descriptive Statistics for the Elements of the Cholesky Factorization Upper Triangle Matrix Γt of the Realized Bipower Covariation Matrix

由表1和表2可知，无论进行何种变换，所得上三角阵各元素都表现出平稳性，ADF检验全部显著拒绝，并基本都表现出长期自相关性，Ljung-Box检验半数以上显著拒绝，因此适合用MHAR模型进行刻画。表1中各元素的峰度大多与3较为接近，表2中各元素的峰度大多显著偏离3，而且表1中部分元素的Jarque-Bera统计量无法拒绝正态分布的原假设。因此进行矩阵对数变换比进行Cholesky分解可以得到各元素更为接近正态分布的列向量Xt，也更适合MHAR模型的OLS估计。另外，表1和表2中上三角阵15个元素的均值和中位数有较大差异，因此MHAR模型设定常数项参数c是15维列向量(变截距)较为合理。

在99%的置信度水平下，在2011年2月1日至2014年10月31日的850个交易日中，BLT联跳检验共检测出504天发生联跳，占总样本的59.294%。因此多资产价格的联跳在中国股票市场并不是偶然现象，而是在宏观经济新闻公告和政策制度等发布的冲击下经常发生，因此有必要考虑引入联跳信息对协方差预测的影响。

为了构建联跳强度序列，首先将2011年2月1日至2013年8月22日的566个交易日(即总样本剔除样本外预测区间)用作估计区间，估计Hawkes模型的参数，得到样本内参数估计值为μ=0.548,α=0.108,β=0.794。将参数代入Hawkes模型，即可构建总样本内的联跳强度时间序列。

4.2 MHAR模型及其扩展模型的样本内拟合

对表1中At上三角阵或者表2中上三角阵Γt进行拉直操作，拉直向量Xt是一个15×1的列向量。为Xt构建基准MHAR模型以及引入联跳的扩展模型，并根据采用的矩阵变换形式，分别命名为LOG-MHAR类模型或者CF-MHAR类模型。表3给出各模型在全样本的参数估计结果和拟合性能比较，其中省略了15维常数列向量c在各模型中的估计值。由于各种扩展MHAR模型与其基准MHAR模型之间均存在嵌套关系，因此表3中还给出对数似然比(LR)检验统计量并标注出显著性。

表3中参数β(d)、β(w)、β(m)的估计结果表明，无论是LOG-MHAR类模型还是CF-MHAR类模型，滞后一日、一月、一周的已实现估计量对预测都有显著的正向影响，日变量的系数小于0.100，周和月变量的系数则在0.300左右，表明中、低频投资者对未来协方差的贡献更大。参数γ和η的估计结果表明，单独引入联跳指示变量时对预测有显著的正向影响，但是其影响较小，系数值仅为0.030左右；单独引入联跳强度时对预测有显著的正向影响，且贡献较大，系数值达到0.625(LOG-MHAR-CI模型)或者0.816(CF-MHAR-CI模型)；而同时引入联跳指示变量和联跳强度时，联跳指示变量对预测不再具有显著影响，联跳强度的贡献则仍然显著为正，且系数值稍有提升。这表明，通过Hawkes模型提炼的联跳强度中蕴含有对于协方差预测更为丰富的信息。

由调整R2及其改进度计算值可知，各个扩展MHAR模型相对于其基准MHAR模型都获得了样本内拟合优度的改进。具体的，CF-MHAR类模型的拟合优度总体高于相应的LOG-MHAR类模型。而LOG-MHAR模型扩展后拟合优度的改进度则高于CF-MHAR模型进行同样扩展后获得的改进度。无论是LOG-MHAR类模型还是CF-MHAR类模型，引入联跳强度都可以带来最大程度的拟合优度提升(0.186%或者0.135%)。各个扩展模型的LR检验统计量都在1%的水平显著，表明即使在对新引入的参数施加惩罚后，引入联跳信息的扩展模型仍然比相应的基准模型有显著更优的样本内拟合性能。

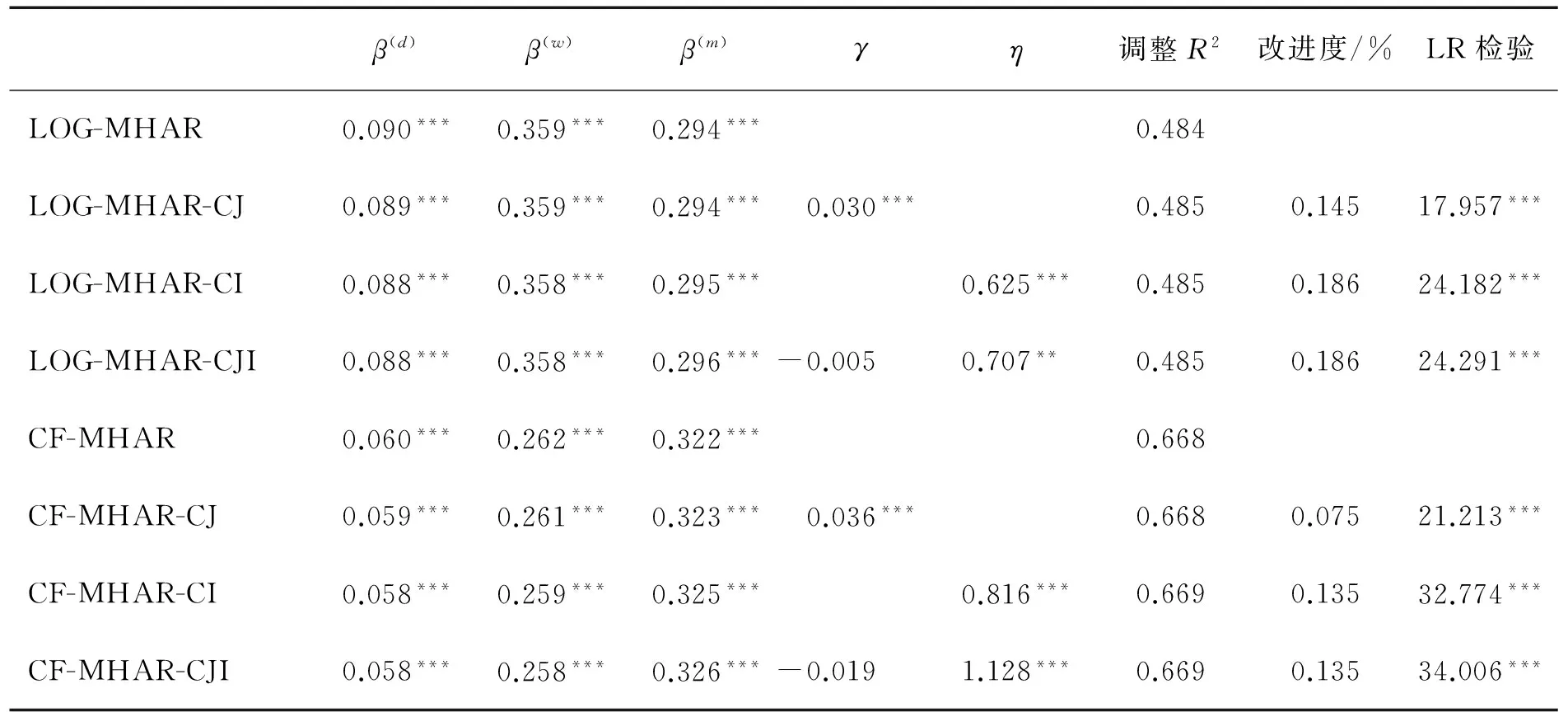
表3 MHAR模型及其扩展模型的全样本参数估计结果Table 3 Parameter Estimation Results of the MHAR Model and Its Extensions(Total Period)

注：***为在1%的水平显著，**为在5%的水平显著。

4.3 MHAR模型及其扩展模型的样本外预测

模型的样本外预测性能是投资者选择协方差预测模型的重要考量，因此本研究将2013年8月23日至2014年10月31日的284个交易日用于协方差模型的样本外预测性能比较。具体的，以566个交易日为估计窗长，采用一步向前滚动预测方法，即先以2011年2月1日至2013年8月22日的566个交易日为估计窗，预测2013年8月23日的协方差，接着以2011年2月2日至2013年8月23日的566个交易日为估计窗，预测2013年8月26日的协方差，以此类推。表4给出各种MHAR模型及其扩展模型的多变量均方误差(MSE)和平均绝对误差(MAE)函数在预测区间的日均值，也给出了扩展模型相对于其基准模型的损失函数值减小量(ΔMSE和ΔMAE)。黑体数据为同一组4个MHAR类模型的最小MSE值或MAE值。

表4表明，无论是LOG-MHAR类模型还是CF-MHAR类模型，引入联跳信息都可以带来预测损失函数值的减小，即样本外预测性能的改善。无论是以MSE指标还是以MAE指标衡量，同时引入联跳指示变量和联跳强度的MHAR-CJI模型都在同组的4个模型中具有最小的损失函数值，即最佳的样本外预测精度。

进一步运用单边DM检验判断引入联跳信息的扩展模型对基准模型样本外预测能力改善的显著性。单边DM检验的零假设是“基准模型和扩展模型的预测能力相同”，备择假设是“扩展模型的预测能力优于基准模型”，预测能力的衡量同样分别考察MSE和MAE两个指标，表5给出各个检验的p值，小于0.100的已标为黑体，表示显著拒绝零假设，即相应扩展模型有显著更优的预测精度。

由表5结果可知，无论是LOG-MHAR类模型还是CF-MHAR类模型，单独引入联跳强度(MHAR-CI模型)以及同时引入联跳指示变量和联跳强度(MHAR-CJI模型)，都可以显著改善基准MHAR模型的MSE和MAE损失函数值，提升协方差样本外预测能力。而如果单独引入联跳指示变量(MHAR-CJ模型)，则仅在MSE指标下有显著的预测性能改进，在MAE指标下预测性能与基准模型并无显著差别。这再次表明Hawkes模型提炼出的联跳强度蕴含着更丰富的协方差预测有益信息。

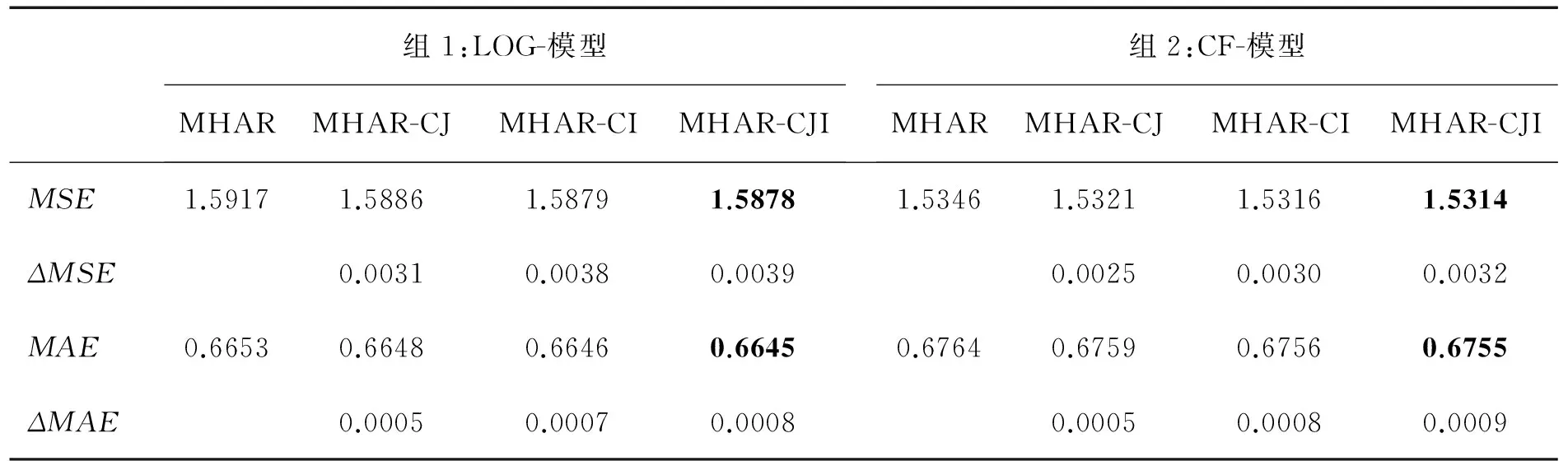
表4 MHAR模型及其扩展模型样本外预测的损失函数Table 4 Out-of-sample Forecasting Losses of the MHAR Model and Its Extensions

表5 MHAR模型及其扩展模型的预测能力DM检验p值Table 5 DM Test p-values for the Forecasting Performance of the MHAR Model and Its Extensions

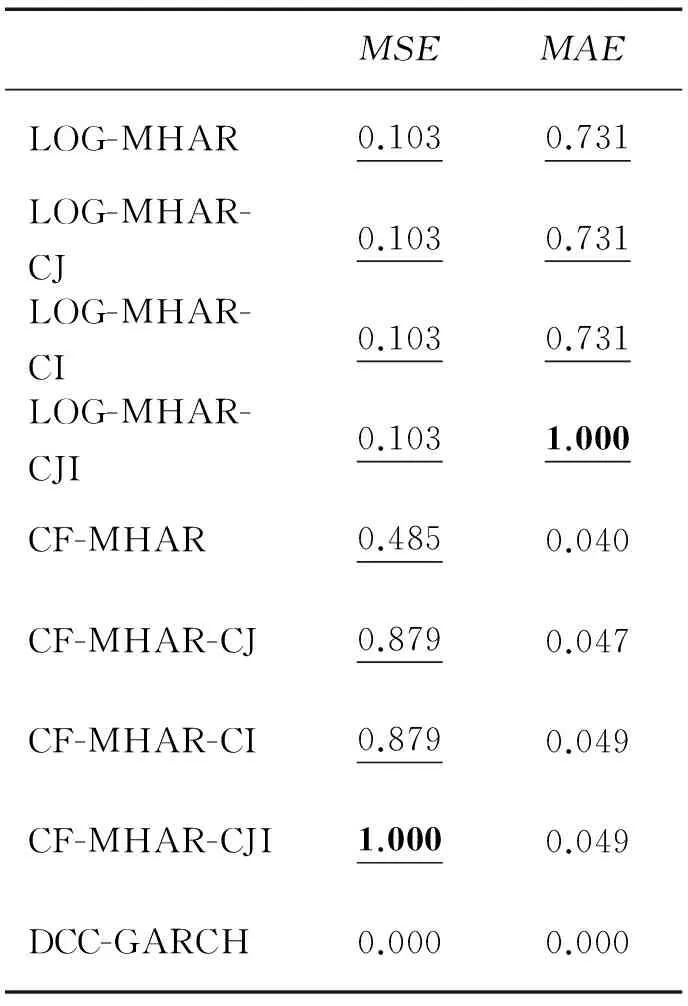
表6 协方差模型预测能力MCS检验p值Table 6 MCS Test p-values for the Forecasting Performance of the Covariance Models

5 结论

本研究对已有基于高频数据的多(>2)资产协方差已实现估计量建模研究进行拓展，考察在预测模型中对联跳信息的引入。以上证50指数成分股中流动性较好且跨不同行业的5只股票5分钟价格为实证数据，通过BLT方法[18]识别多资产价格联跳，发现联跳天数占总样本的59.294%，因此联跳在中国股票市场并非偶然现象，而是在宏观经济新闻公告和政策制度发布的冲击下经常发生，本研究选题具有实际意义。以多元异质自回归(MHAR)模型为基础，分别及同时引入取值0/1的联跳指示变量和Hawkes模型[23]估计的联跳强度，扩展出MHAR-CJ模型、MHAR-CI模型和MHAR-CJI模型。为了确保预测协方差矩阵的正定性，先对协方差已实现估计量进行矩阵对数变换[8]或者Cholesky分解[9]，为变换后的序列构建(扩展的)MHAR模型进行预测后，再重构出协方差矩阵，并将相应模型分别命名为LOG-MHAR类模型和CF-MHAR类模型。

首先，根据全样本参数估计结果可以发现，无论是LOG-MHAR类模型还是CF-MHAR类模型，联跳强度的贡献始终较大而且显著为正，引入联跳强度后的扩展模型比基准模型都有最大程度的拟合优度提升，表明通过Hawkes模型提炼的联跳强度蕴含着更丰富的协方差预测有益信息，这一信息的引入能显著提升模型的样本内拟合性能。其次，在样本外预测性能方面，通过对MSE和MAE损失函数值的比较以及在MSE和MAE指标下的DM检验可知，无论是LOG-MHAR类模型还是CF-MHAR类模型，引入联跳强度后的模型相对于基准模型都有统计意义上显著更高的预测精度；而在经济意义层面，通过将各MHAR类模型的样本外预测应用于GMVP策略可以发现，引入联跳强度变量能够降低投资组合方差。因此，样本外的检验结果与样本内一致，同样揭示了联跳强度所蕴含的协方差预测有益信息。此外，在MSE、MAE和组合方差指标下进行MCS检验的结果表明，在MSE指标下CF-MHAR类模型相对优于LOG-MHAR类模型，但优势并不显著；而在MAE和组合方差指标下LOG-MHAR类模型都显著胜出CF-MHAR类模型，其中LOG-MHAR-CJI模型则是引入联跳信息的最优形式。

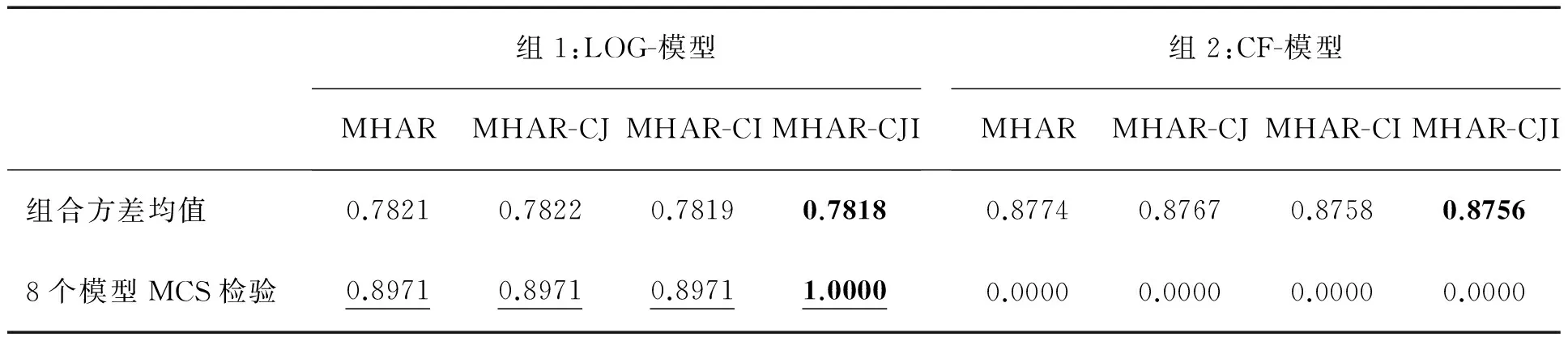
表7 协方差模型用于GMVP策略的组合方差Table 7 GMVP Strategy′s Portfolio Variance of the Covariance Models

本研究的实证结果具有明确的经济含义，跨行业多资产价格的联跳往往是由能影响整个资本市场的宏观信息导致的，基准MHAR模型的回归量中仅包含单资产方差及两两资产之间协方差的信息，而未考虑到宏观信息的影响；在多资产协方差模型中引入联跳信息，也就相当于将历史信息中反映市场宏观信息的部分包含在解释变量中。引入联跳后模型拟合及预测能力的显著改善以及将协方差预测应用到GMVP资产配置策略后组合风险的降低，都证明了这些宏观信息对多资产协方差预测有较显著的贡献，肯定了在协方差预测模型中引入联跳的重要价值。本研究的结论对于金融管理者和投资者进行金融风险管理及资产配置都具有实际指导意义。

本研究仅是在多(>2)资产协方差已实现估计量预测模型中引入联跳的初步探索，以此为基础进一步拓展的方向包括：①从多资产协方差预测拓展到包含数十乃至上百资产的超高维协方差预测，以更好地满足实务需求，其中对超高维矩阵的处理可以借鉴HAUTSCH et al.[32]的分块正则化(blocking and regularization,BnR)方法，并基于随机矩阵理论(random matrix theory,RMT)对超高维矩阵合理去噪[33]。②全面比较采用各种协方差已实现估计量以及常用协方差模型[11]时引入联跳的合理方式和效果，进一步探索预测结合技术应用带来的预测性能改善，为实务应用提供更准确的协方差预测模型。

[1]ANDERSEN T G,BOLLERSLEV T.Answering the skeptics:yes,standard volatility models do provide accurate forecasts.InternationalEconomicReview,1998,39(4):885-905.

[2]BARNDORFF-NIELSEN O E,SHEPHARD N.Econometric analysis of realized covariation:high frequency based covariance,regression,and correlation in financial economics.Econometrica,2004,72(3):885-925.

[3]BARNDORFF-NIELSEN O E,SHEPHARD N.Measuringtheimpactofjumpsinmultivariatepriceprocessesusingbipowercovariation.Aarhus:University of Aarhus,2004.

[4]ZHANG L.Estimating covariation:epps effect,microstructure noise.JournalofEconometrics,2011,160(1):33-47.

[5]BARNDORFF-NIELSEN O E,HANSEN P R,LUNDE A,et al.Multivariate realised kernels:consistent positive semi-definite estimators of the covariation of equity prices with noise and non-synchronous trading.JournalofEconometrics,2011,162(2):149-169.

[6]刘丽萍,马丹.基于流动性调整的高频协方差阵的估计及其应用研究.管理工程学报,2016,30(2):76-83.

LIU Liping,MA Dan.Estimation and application study on covariance matrix of high frequency data based on liquidity adjustment.JournalofIndustrialEngineeringandEngineeringManagement,2016,30(2):76-83.(in Chinese)

[7]赵树然,姜亚萍,任培民.高频波动率矩阵估计的比较分析:基于有噪非同步的金融数据.中国管理科学,2015,23(10):19-29.

ZHAO Shuran,JIANG Yaping,REN Peimin.Comparing estimators of the high-frequency volatility matrix in the presence of non-synchronous trading and market microstructure noise.ChineseJournalofManagementScience,2015,23(10):19-29.(in Chinese)

[8]BAUER G H,VORKINK K.Forecasting multivariate realized stock market volatility.JournalofEconometrics,2011,160(1):93-101.

[9]CHIRIAC R,VOEV V.Modelling and forecasting multivariate realized volatility.JournalofAppliedEconometrics,2011,26(6):922-947.

[10] CORSI F.A simple approximate long-memory model of realized volatility.JournalofFinancialEconometrics,2009,7(2):174-196.

[11] VARNESKOV R,VOEV V.The role of realized ex-post covariance measures and dynamic model choice on the quality of covariance forecasts.JournalofEmpiricalFinance,2013,20:83-95.

[12] HAUTSCH N,KYJ L M,MALEC P.Do high-frequency data improve high-dimensional portfolio allocations?.JournalofAppliedEconometrics,2015,30(2):263-290.

[13] 韩立岩,任光宇.基于已实现二阶矩预测的期货套期保值策略及对股指期货的应用.系统工程理论与实践,2012,32(12):2629-2636.

HAN Liyan,REN Guangyu.Hedging strategy with futures based on prediction of realized second moment:an application to stock index futures.SystemsEngineering-Theory&Practice,2012,32(12):2629-2636.(in Chinese)

[14] WANG H,YUE M,ZHAO H.Cojumps in China′s spot and stock index futures markets.Pacific-BasinFinanceJournal,2015,35:541-557.

[15] 唐勇,林欣.考虑共同跳跃的波动建模:基于高频数据视角.中国管理科学,2015,23(8):46-53.

TANG Yong,LIN Xin.Volatility modeling in consideration of the co-jumps:based on the perspective of high-frequency data.ChineseJournalofManagementScience,2015,23(8):46-53.(in Chinese)

[16] 刘丽萍.多维金融高频协方差阵预测模型的比较分析.数学的实践与认识,2014,44(12):203-214.

LIU Liping.The comparative analysis of multidimensional financial high frequency covariance matrix′s prediction model.MathematicsinPracticeandTheory,2014,44(12):203-214.(in Chinese)

[17] 刘丽萍,张国帅,白万平.估计量和预测模型的选择对高频协方差阵的预测及组合收益的影响.系统工程,2015,33(8):140-146.

LIU Liping,ZHANG Guoshuai,BAI Wanping.Choice of the impact of estimator and predictive model on the forecast of high-frequency covariance and portfolio returns.SystemsEngineering,2015,33(8):140-146.(in Chinese)

[18] BOLLERSLEV T,LAW T H,TAUCHEN G.Risk,jumps,and diversification.JournalofEconometrics,2008,144(1):234-256.

[19] LAHAYE J,LAURENT S,NEELY C J.Jumps,cojumps and macro announcements.JournalofAppliedEconometrics,2011,26(6):893-921.

[20] GILDER D,SHACKLETON M B,TAYLOR S J.Cojumps in stock prices:empirical evidence.JournalofBanking&Finance,2014,40:443-459.

[21] DUNGEY M,HVOZDYK L.Cojumping:evidence from the US treasury bond and futures markets.JournalofBanking&Finance,2012,36(5):1563-1575.

[22] CLEMENTS A E,LIAO Y.Theroleinindexjumpsandcojumpsinforecastingstockindexvolatility:evidencefromtheDowJonesindex.Brisbane:National Centre for Econometric Research(NCER),2014.

[23] HAWKES A G.Spectra of some self-exciting and mutually exciting point processes.Biometrika,1971,58(1):83-90.

[24] DIEBOLD F X,MARIANO R S.Comparing predictive accuracy.JournalofBusiness&EconomicStatistics,1995,13(3):253-263.

[25] HANSEN P R,LUNDE A,NASON J M.The model confidence set.Econometrica,2011,79(2):453-497.

[26] 瞿慧,刘烨.沪深300指数收益率及已实现波动联合建模研究.管理科学,2012,25(6):101-110.

QU Hui,LIU Ye.A joint model for CSI 300 index return and realized volatility.JournalofManagementScience,2012,25(6):101-110.(in Chinese)

[27] BOUDT K,CROUX C,LAURENT S.Robust estimation of intraweek periodicity in volatility and jump detection.JournalofEmpiricalFinance,2011,18(2):353-367.

[28] BECKER R,CLEMENTS A E,DOOLAN M B,et al.Selecting volatility forecasting models for portfolio allocation purposes.InternationalJournalofForecasting,2015,31(3):849-861.

[29] 魏宇,马锋,黄登仕.多分形波动率预测模型及其MCS检验.管理科学学报,2015,18(8):61-72.

WEI Yu,MA Feng,HUANG Dengshi.Multi-fractal volatility forecasting model and its MCS test.JournalofManagementSciencesinChina,2015,18(8):61-72.(in Chinese)

[30] 张玉鹏,洪永淼.基于广义谱和MCS检验的VaR模型预测绩效评估.管理科学,2015,28(4):108-119.

ZHANG Yupeng,HONG Yongmiao.Evaluating predictive performance of value-at-risk models based on generalized spectrum and MCS tests.JournalofManagementScience,2015,28(4):108-119.(in Chinese)

[31] 吴恒煜,夏泽安,聂富强.引入跳跃和结构转换的中国股市已实现波动率预测研究:基于拓展的HAR-RV模型.数理统计与管理,2015,34(6):1111-1128.

WU Hengyu,XIA Ze′an,NIE Fuqiang.Research on Chinese stock market realized volatility forecasting with jumps and structure changes:based on expanded HAR-RV models.JournalofAppliedStatisticsandManagement,2015,34(6):1111-1128.(in Chinese)

[32] HAUTSCH N,KYJ L M,OOMEN R C A.A blocking and regularization approach to high dimensional realized covariance estimation.JournalofAppliedEconometrics,2012,27(4):625-645.

[33] 李冰娜,惠晓峰,李连江.基于蒙特卡洛RMT去噪法小股票组合风险优化研究.管理科学,2016,29(2):134-145.

LI Bingna,HUI Xiaofeng,LI Lianjiang.Research on risk optimization of small stock portfolio based on the filtering method of RMT using Monte Carlo simulation.JournalofManagementScience,2016,29(2):134-145.(in Chinese)

TheRoleofCojumpsinForecastingCovarianceMatricesinChineseStockMarkets:AStudyBasedontheMultivariateHARModel

QU Hui，JI Ping

School of Management and Engineering, Nanjing University, Nanjing 210093, China

The time-varying covariance matrix of the financial assets is the key for financial applications such as portfolio allocation and risk management. Previous studies on covariance matrix forecasting use daily or even lower frequency data, causing the problems of parameter estimation difficulty and curse of dimensionality.

With intraday high-frequency data, non-parametric estimators of the covariance matrix can be constructed. This turns the covariance matrix from hidden to an observable variable that can be directly modeled, thus reducing the complexity of covariance model estimation and increasing the applicability of covariance models in high-dimension applications. Furthermore, with high-frequency data, cojumps can be identified, which refers to jumps of multiple asset prices in the same intraday sampling interval. Cojumps are often triggered by macroeconomic news announcements and policy releases, and such macro-information will eventually be absorbed and reflected in the covariance matrix. Thus, we argue that cojumps may contain information beneficial for covariance forecasting and propose to identify cojumps and use them in the covariance forecasting models.

The multivariate heterogeneous autoregressive(MHAR) model is used as the benchmark model for the nonparametric covariance matrix estimator. The cojump indicators and the cojump intensities estimated by the Hawkes model are included as additional predictors, first separately and then simultaneously. Based on the mean squared error and the mean absolute error criteria, the three extended MHAR models are each compared with the benchmark using the Diebold Mariano test in terms of their out-of-sample forecast performance. The model confidence set test is then used to identify the best models. Besides, the out-of-sample forecasts are used in the global minimum variance portfolio strategy to justify the economic value of the extended models.

We consider five high liquidity stocks from different sectors of the SSE 50 index and employ their five-minute prices. Empirical results show that: ①compared with the cojump indicators, the cojump intensities have more significant contribution to covariance matrix forecasting; ②incorporating the cojump intensities can significantly improve the fit and forecast performance of the MHAR model; ③the extended MHAR model that uses matrix log transformation to ensure positive definiteness and incorporates both the cojump intensities and the cojump indicators is superior, both statistically and economically.

The above results confirm the role of cojumps in forecasting covariance matrices in Chinese stock markets, as well as reveal the contribution of macro-information to covariance forecasting. This study provides practical guidance for financial managers and investors in their financial risk management and asset allocation practices.

covariance forecasting；cojump；multivariate heterogeneous autoregressive model；Hawkes model；model confidence set(MCS) test；global minimum variance portfolio

Date:June 14th, 2016

DateOctober 9th, 2016

FundedProject:Supported by the National Natural Science Foundation of China(71671084,71201075) and the Specialized Research Fund for the Doctoral Program of Ministry of Education of People′s Republic of China(20120091120003)

Biography:QU Hui, doctor in philosophy, is an associate professor in the School of Management and Engineering at Nanjing University. Her research interests include financial risk management and investment decisions. Her representative paper titled “Forecasting realized volatility in electricity markets using logistic smooth transition heterogeneous autoregressive models” was published in theEnergyEconomics(Vol 54, 2016). E-mail： linda59qu@nju.edu.cn

JI Ping is a master degree in the School of Management and Engineering at Nanjing University. Her research interest focuses on financial engineering. Her representative paper titled “Modeling realized volatility dynamics with a genetic algorithm” was published in theJournalofForecasting(Issue 5, 2016). E-mail：belinda_nju@163.com

F830.91

A

10.3969/j.issn.1672-0334.2016.06.003

1672-0334(2016)06-0028-11

2016-06-14修返日期2016-10-09

国家自然科学基金(71671084,71201075)；教育部高等学校博士学科点专项科研基金(20120091120003)

瞿慧，哲学博士，南京大学工程管理学院副教授，研究方向为金融风险管理与投资决策等，代表性学术成果为“Forecasting realized volatility in electricity markets using logistic smooth transition heterogeneous autoregressive models”，发表在2016年第54卷《Energy Economics》，E-mail：linda59qu@nju.edu.cn

纪萍，南京大学工程管理学院硕士研究生，研究方向为金融工程等，代表性学术成果为“Modeling realized volatility dynamics with a genetic algorithm”，发表在2016年第5期《Journal of Forecasting》，E-mail：belinda_nju@163.com

□