钻孔DMI应变计法测定点焊残余应力基础研究

陈忠安，厉鸿森，赵玉津，金学松

(1.江苏大学 土木工程与力学学院，江苏 镇江 212013；2.美国南卡罗莱娜大学 机械工程系，奥兰治堡 29118；3．天津大学 材料学院，天津 300072；4.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)



钻孔DMI应变计法测定点焊残余应力基础研究

陈忠安1，厉鸿森1，赵玉津2,3，金学松4

(1.江苏大学 土木工程与力学学院，江苏 镇江 212013；2.美国南卡罗莱娜大学 机械工程系，奥兰治堡 29118；3．天津大学 材料学院，天津 300072；4.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

针对目前测定点焊残余应力的方法在工程应用上的局限性，提出了将DMI应变计与钻孔法相结合的钻孔DMI应变计法。通过建立点焊件的力学模型，推导得到了钻孔DMI应变计法基本方程，并由数值标定的方法得到释放系数表。结合示例验证了该方程的正确性，同时也简述了测量的具体步骤。并采用有限元模拟的方法，从工件的最小边距、连接件尺寸、焊点直径与板厚比、钻孔深度4个方面分析了钻孔DMI应变计法的适用范围。

钻孔法；DMI应变计；点焊残余应力；有限元模拟；释放系数

电阻点焊作为一种易于实现自动化的焊接方法，被广泛用于航空航天、汽车等多种制造领域[1-2]。点焊过程中产生的残余应力对工件强度、稳定性及疲劳寿命有直接的影响[2]，因此准确了解点焊残余应力在焊接结构中的分布规律，具有重要意义。目前，用于研究点焊残余应力的方法有X射线法、云纹法和传统钻孔法。其中，X射线法的测试设备较为复杂，对测试表面要求较高[3]；云纹法主要与钻孔法结合，但贴光栅、处理条纹和数据较为繁琐[4]。因此，这两种方法在工程应用时会受到一定限制。点焊残余应力沿径向的变化梯度大，传统钻孔法不适用于这种应力梯度变化大的残余应力场[5]。

因此，本文提出了DMI光学应变计与钻孔法相结合的钻孔DMI应变计法，并建立该方法的基本方程，为后续研究提供基础理论。此外，文中通过有限元模拟，从点焊工件尺寸、钻孔深度等方面分析了钻孔DMI应变法的适用性。

1 钻孔DMI应变计法基本方程的建立

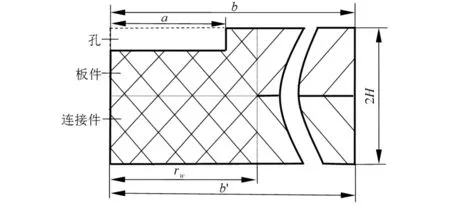
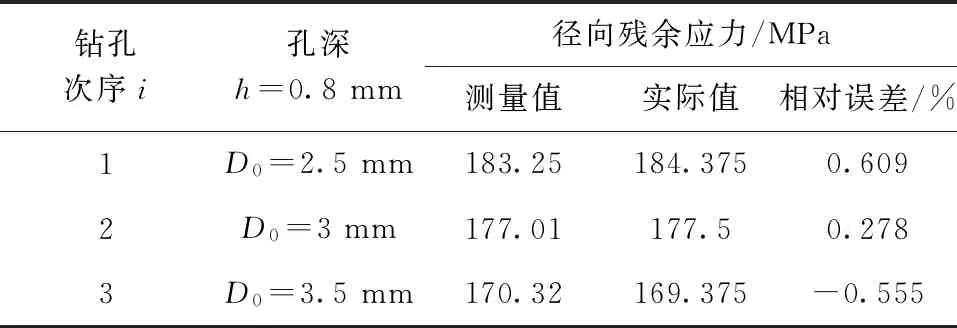
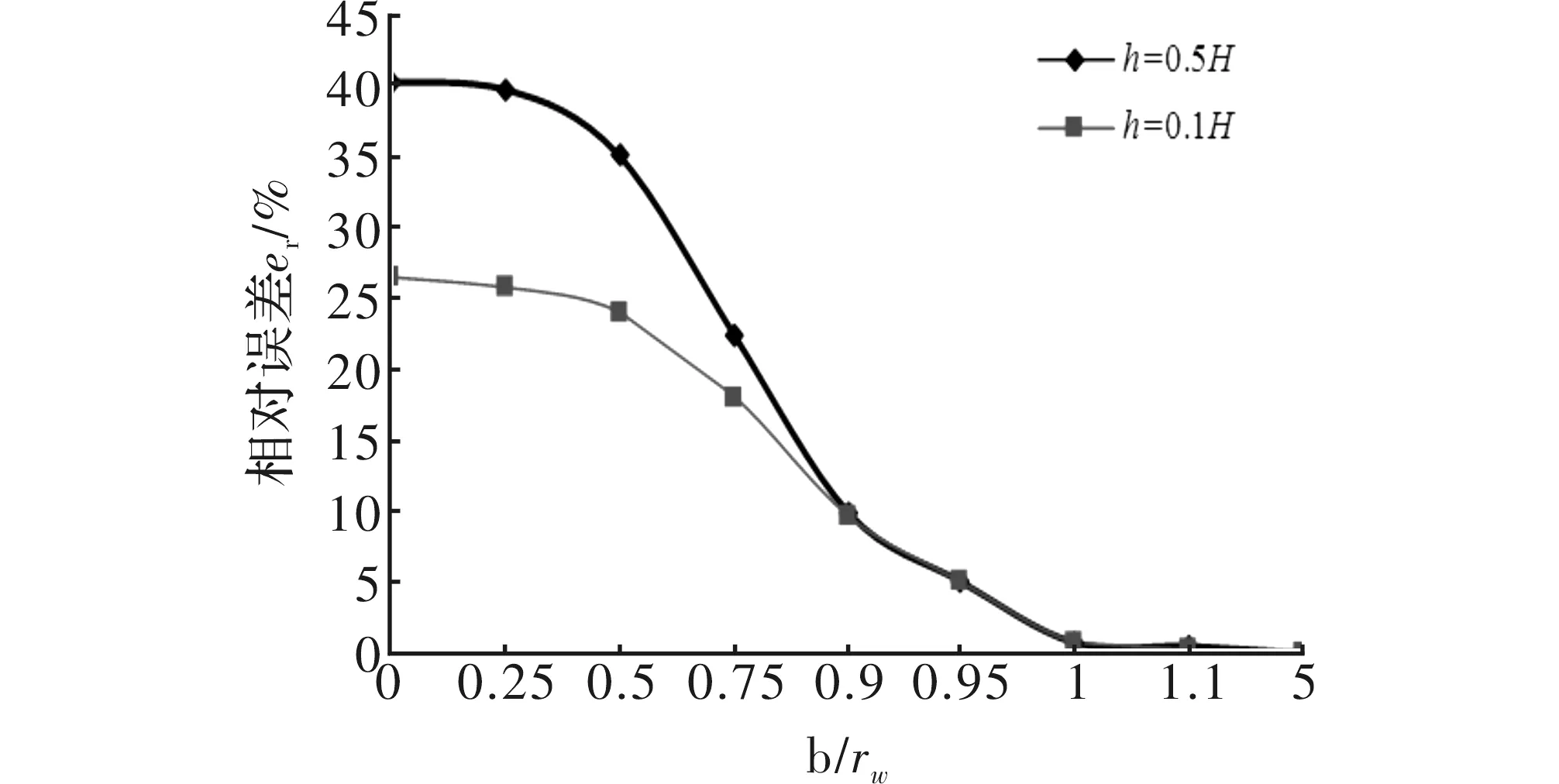
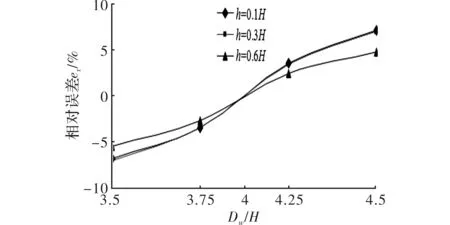
点焊残余应力场以焊点为中心，呈轴对称分布[6]；且残余应力主要集中在融合区域，在距离焊点较远区域内残余应力较小，可忽略不计[7]。故以焊点为圆心，远大于焊点半径rw的长度b为半径取分离体，且外边界处残余应力可忽略。在焊点处对中钻一孔径2a(a

(1)

其中，E为弹性模量；ν为泊松比。

工程实测中，通常只需钻盲孔。而盲孔附近应力分布与通孔类似，故引入释放系数K。则盲孔情况下，孔壁处径向残余应力为

(2)

仅对中钻一次孔的情况下，只能测得孔边径向残余应力p，而释放的周向残余应力q则无法测得。极坐标系下轴对称问题中p与q的平衡方程[8]为

(3)

测量中，径向残余应力分布函数通常是未知的，故由式(3)不能计算出孔边周向残余应力。此时，引进差分法，通过测定不同孔径下的径向残余应力，再由差分公式计算出孔边周向残余应力，表达式为

(4)

2 释放应变的测量

根据点焊残余应力场的轴对称分布规律，选择DMI环形应变计。在DMI应变计内圈、外圈测点所在圆周上各均分布着36个节点，通过输出节点坐标变化可得到对应节点的周向应变。

(5)

通过上式将DMI应变计输出的周向应变转换成焊点边界处的周向应变，用于残余应力的计算。

3 释放系数的标定

3.1 标定模型的建立

利用有限元软件Abaqus建立双板等厚(单板厚H)点焊轴对称模型，如图1所示[9]。其中，焊点直径Dw与焊接板厚度H比值为4，半径b′=b=10rw，模型材料为各向同性线弹性材料。

图1 点焊工件的截面图

3.2 释放系数的标定

为保证点焊残余应力在钻孔深度上均匀分布，每次钻孔增量Δh为0.1[10]。在孔壁处作用单位力，得释放系数K，如表1所示。其中，释放系数K已无量纲化，D0为钻孔直径；h为钻孔深度。

为便于工程实际应用，对表1中的释放系数K拟合，得到置信度95%以上的函数K(A,B)

K(A,B)=f0+f1A+f2B+f3A2+f4B2+f5AB+f6A3+f7B3+f8AB2+f9A2B

(6)

其中，A=h/DW、B=D0/DW，各项系数fi(i=0,1,…,9)值，如表2所示。

表2 K函数的系数值

4 点焊残余应力的测定示例验证

以弹性模量E=71.7 GPa，泊松比ν=0.33的铝合金点焊工件为例，单层板厚1 mm，焊点直径4 mm。板件与连接板连接部分是40 mm×40 mm的方形区域。假设焊点内残余应力沿厚度均匀分布，即

σr=(-10r2+200), 0≤r≤5

其中，r是距焊点中心的距离。测定r=1.5 mm处的径向和周向残余应力。

(1)DMI应变计和钻头的选取。根据测点位置和测定要求，选取实际尺寸4.38 mm×6.4 mm的DMI应变计，对准焊点中心粘贴在工件表面。钻头尺寸选择φ=2.5 mm,3 mm和3.5 mm；

(2)钻孔测量。按照表3中的次序中心钻孔。将测量值代入式(5)得焊点边界处周向应变，如表3所示。

表3 周向应变的测量值

(3)求解径向残余应力。通过查表1或式(6)，得释放系数K。求得的εθ0,i与相应K值代入式(2)，得到径向残余应力pi，如表4所示。

表4 径向残余应力的测量值与实际值

由表4可知，径向残余应力测量值与实际值的误差<1%，即基本方程式(2)是正确、可行的；

(4)求解周向残余应力。由表4可得，a3-a1=0.5 mm，p3-p1=-12.93 MPa，代入式(3)得周向残余应力q2；实际值由示例中的场函数根据式(3)求得，如表5所示。

表5 周向残余应力的测量值与实际值

由表5可知，周向残余应力测量值与实际值的误差<5%，即由轴对称的平衡方程求解周向残余应力是正确、可行的。

5 方法的适用性

释放系数K是由标定模型得到的。对于释放系数K在其它尺寸、材料的点焊工件是否适用，需进一步分析。具体如下：

(1)最小板边距的影响。在实际点焊工件中，焊件板最小边距bmin≠10rw时，会引起测量结果误差[11]。放系数K的相对误差er随b的变化曲线，如图2所示。当深度相同时，er随b增大而减小。当b≥5rw时，在整个深度H上，er<5%在工程允许的误差范围。因而，焊点到工件的最小板边距b≥5rw时，标定得到的释放系数仍可用；

(2)连接件尺寸对测量结果的影响。在实际点焊工件中，连接板与板仅有部分连接。当连接件的尺寸b′≠b时，可能影响测量结果的准确。er随b′的变化曲线，如图3所示。在深度相同时，er随b′增大而减小。当b′在0～rw(含0)时，er>5%，超过工程许可的范围；当连接件尺寸b′≥rw时，er≤1%。因而，对于b′≥rw的点焊工件，释放系数仍可用；

图2 相对误差随b的变化曲线

图3 相对误差随b′的变化曲线

(3)Dw/H的适用范围。在工程实际中，焊点直径Dw与焊接板厚度H的比值都分布在3～5之间[12]，当Dw/H≠4时，会引起测量结果的误差。er随Dw/H的变化曲线，如图4所示。深度相同时，当Dw/H<4时，er随Dw/H增大而减小；当Dw/H>4时，er随Dw/H增大而增大。当Dw/H在3.75～4.25时，er<5%在工程允许的误差范围内。因而，当工件的焊点直径与板厚比在3.75～4.25时，释放系数仍可用；

(4)最小钻孔深度的确定。随点焊技术在镁铝等金属中的应用，泊松比范围已扩大到0.25～0.35[13- 14]。通孔状态下，K与泊松比ν无关[15]。当钻孔深度较浅时，ν对释放系数的影响较大，会影响测量结果准确性。er随h的变化曲线，如图5所示。随深度增加，不同泊松比对应的er逐渐减小。当0.28≤ν≤0.33时，整个深度上er<4%。当0.25≤ν<0.28时，在0.15H≤h≤H内er<5%。当0.33<ν≤0.35时，在0.2H≤h≤H内er<5%。因而，根据材料的泊松比可确定最小的钻孔深度。

图4 相对误差随Dw/H的变化曲线

图5 相对误差随深度h的变化曲线

6 结束语

(1)针对工程上点焊残余应力实测方法的空白，提出了钻孔DMI应变计法。DMI应变计的引入使得工程测量点焊残余应力更为方便、精确；(2)通过示例，验证了钻孔DMI应变计法基本方程的正确性。该方程的建立，不仅为研究沿厚度非均匀分布的点焊残余应力提供了理论基础，也为点焊残余应力的计算提供了基本算式；(3)针对点焊的标定模型，分析了板件和连接板的半径、焊点直径与板厚比(Dw/H)及材料泊松比的影响，确定了钻孔DMI应变法适用的点焊工件尺寸范围和最小钻孔深度。

[1] 袁少波,董彦刚.点焊技术在汽车工业中的应用[J].电焊机,2005,35(2):26-29.

[2] 王伟伟,宇慧平,刘赵淼.电阻点焊力学特性的研究进展[J].焊接技术,2011,40(7):1-4.

[3] 王庆明,孙渊.残余应力测试技术的进展与动向[J].机电工程,2011,28(1):11-15.

[4] 陈巨兵,彭勇晟,赵社戌,等.钻孔法中光栅应变花与电阻应变花测量变形的比较[J].上海交通大学学报,2009,43(10):1636-1639.

[5] Sanjeev K Khanna,Canlong He,Hari N Agrawal. Residual stress measurement in spot welds and the effect of fatigue loading on redistribution of stresses using high sensitivity moire′ interferometry[J].Transactions of the ASME,2001,12(3):132-138.

[6] Moshayedi H,Iradj Sattari Far.Resistance spot welding and the effects of welding time and current on residual stresses[J].Journal of Materials Processing Technology,2014,21(4):2545-2552.

[7] 米茂谷.残余应力的产生和对策[M].北京:机械工业出版社,1983.

[8] Timoshenko S P,Goodier J N.Theory of elasticity[M].NY,USA:McGraw-Hill Book Company,1970.

[9] 雷鸣,王敏,殷关庆.镀锌钢板点焊过程的有限元模拟[J].上海交通大学学报,2005,39(7):1033-1037.

[10] Schajer G S.Practical residual stress measurement methods[M].New York,USA:John Wiley & Sons Ltd,2013.

[11] 周景,杜坤.汽车镀锌板点焊规范研究[J].合肥工业大学学报:自然科学版,2007,30(z1):132-135.

[12] 张文扬,郭绍庆,梁海,等.关于点焊板厚与熔核最小直径及最小抗剪强度的关系的讨论[C].镇江:第十六次全国焊接学术会议,2011.

[13] 谢列卫,刘勇,潘海华.铝合金材料残余应力测试的钻孔法研究[J].机械强度,1995,17(1):32-35.

[14] 冯吉才,王亚荣,张忠典.镁合金焊接技术的研究现状及应用[J].中国有色金属学报,2005,15(2):165-178.

[15] ASTM International.Standard test method for determining residual stresses by the hole-drilling strain-gage method,ASTM E837-08e1[S].West Conshohocken, PA,USA:ASTM International,2008.

The Fundamental Research of Residual Stresses Measuring in Spot Welding By Hole Drilling DMI Strain Gauge Method

CHEN Zhongan1，LI Hongsen1，CHAO Yujin2，3，JIN Xuesong4

(1. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China; 2. Department of Mechanical Engineering, University of South Carolina,Orangeburg 29118, USA; 3. School of Material Science, Tianjin University, Tianjin 300072, China; 4. Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China)

In view of the limitation of the current method for measuring residual stress of spot welding on engineering application, the DMI strain gauge method is proposed, which combines the DMI strain gauge with the drilling method. By establishing the mechanical model of spot welding work piece, the basic equation of DMI strain gauge hole drilling method is deduced, and by the method of numerical can be obtained the release coefficient table. The example verify the correctness of the basic equation, and also illustrates the specific steps of measuring. Finally, using the finite element method, from the minimum margins, workpiece size, spot diameter and connection plate thickness ratio, drilling depth four aspects analyzes the scope of application of DMI drilling strain gauge method.

hole drilling method; DMI strain gauge; welding residual stress; finite element simulation; release coefficients

10.16180/j.cnki.issn1007-7820.2016.12.032

2016- 02- 21

厉鸿森(1988-)，女，硕士研究生。研究方向：点焊残余应力的测量和计算。

O348；TB121

A

1007-7820(2016)12-114-04