广义估计方程在糖尿病并发症影响因素分析中的应用*
吴 彬 曹建平 邹煌秀 徐宝川 林佳荣
广义估计方程在糖尿病并发症影响因素分析中的应用*
吴 彬1曹建平2邹煌秀3徐宝川1林佳荣1
目的探讨广义估计方程在糖尿病并发症影响因素研究中的应用。方法对570例2型糖尿病患者的基本情况、生活方式和糖尿病患病情况等进行问卷调查,采用广义估计方程分析并发症的危险因素。结果患病时间、血糖水平和体质量指数是影响糖尿病并发症发生的主要因素。结论广义估计方程可较好分析疾病多种结局的影响因素。
广义估计方程 糖尿病 并发症 影响因素
糖尿病最重要的危害就在于其并发症的发生,并发症可导致伤残和早死,严重影响患者的生活质量。分析糖尿病并发症影响因素传统的做法是把并发症作为应变量,各种危险因素作为自变量,采用logistic回归模型分析自变量与应变量的关系。一种是设有并发症为1,无并发症为0,采用两分类的logistic模型进行分析,另一种是把并发症的个数作为应变量,采用有序logistic模型来进行统计分析[1-2]。但一个糖尿病患者,可能目前没有并发症,也可能伴发一种或多种并发症,不同人并发症的个数相同但种类可能不同,故传统分析把并发症发生情况作为一个应变量不太合适,应该用多个应变量表示并发症发生情况,不同并发症发生可能存在相关性,即多个应变量存在关联。分析此类数据采用上述两种统计方法将丢失大量有用的信息。广义估计方程是Liang和Zeger在广义线性模型的基础上提出的,它可以分析传统方法无法分析的多个定性应变量且应变量之间存在相关性的资料,得到的参数估计值稳健、可靠[3]。本文采用广义估计方程分析糖尿病并发症的危险因素,以期为其他研究者在处理疾病多种结局数据时提供参考。
资料与方法
1.调查对象
选择2015年1月至2015年2月到福建省某三甲医院内分泌科就诊的600例2型糖尿病患者(诊断依据1999年WHO修订的糖尿病诊断标准[4]),纳入标准为病程在6个月以上、年龄18~80岁、目前无急性并发症的患者,排除文盲病例,糖尿病并发症由门诊医生确诊。
2.调查内容
采用自行设计调查表进行调查,调查项目包括患者的基本情况:年龄、性别、身高、体重、文化程度、压力状况等;患病及治疗情况:患病年龄、血糖水平、血压水平、用药情况、治疗费用、并发症等:生活方式:吸烟、喝酒、饮食、运动等。血糖和血压水平为离调查时间最近的测定结果。
3.调查方法
由经过培训的福建医科大学公共卫生学院研究生和本科实习生在门诊医生允许的条件下对就诊的2型糖尿病患者进行面对面问卷调查,问卷填写完毕后当场检查回收,收回有效问卷570份。
4.数据统计分析方法和原理
拟合广义估计方程模型[3,5-7]。
假设有n个观察对象,每个观察对象可能发生P种并发症,第 i个观察对象(i=1,2,…,n)第 j(j=1,2,…,p)种并发症发生情况记为 Yij(Yij=0,未患第 j种并发症,Yij=1,患第 j种并发症),Xij(Xij1,Xij2,…,Xijm)为与Yij相对应的自变量向量。不同观察对象之间的观察值相互独立,同一观察对象的多种并发症发生与否存在相关。广义估计方程的模型结构如下:
(1)Yij的期望为 E(Yij),有
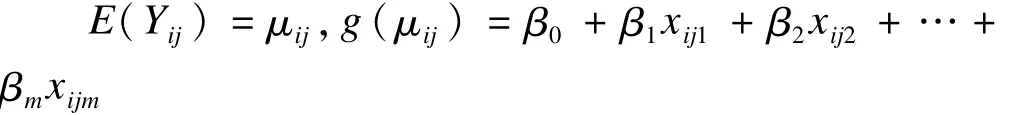
其中,g(μij)为联接函数,可根据数据类型选取合适的联接函数。本次选择Binary logistic作为联接函数。
(2)Yij的方差为 Var(Yij),有
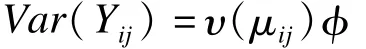
其中υ(μij)为已知方差函数,φ表示尺度参数,表示Y的方差不能被υ(μij)解释的部分。
(3)第i个观察对象发生P种并发症存在相关性,可用P×P维“作业相关矩阵”Ri(α)来表示,α又叫相关参数。
(4)Ri(α)对应的作业协方差阵为
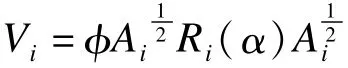
Ai为P×P维对角矩阵,其对角元素为υ(μij)广义估计方程为:
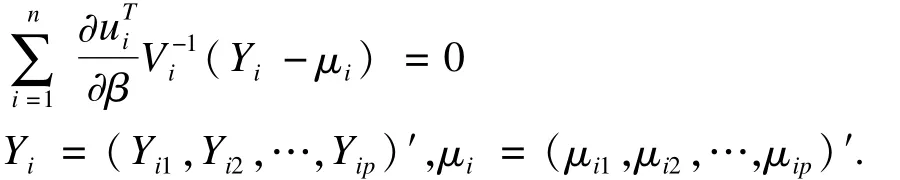
模型求解:假设多个测量值之间无相关性,按广义线性模型计算β的估计值,作为迭代运算的β初始值。求出φ,α后修正β,直至收敛。本研究将糖尿病并发症分成视网膜病变、肾脏病变、糖尿病皮肤病、糖尿病足、神经病变、心脑血管病变和其他7类。由于无法确定各种并发症的相关结构,故采用无结构的作业相关矩阵。患者年龄、性别、文化程度、患病时间、吸烟、饮酒、血糖情况等作为自变量拟合广义估计方程模型。应变量和自变量的赋值情况见表1。所有的数据用PASW 18.0和SAS9.0统计软件分析处理。广义估计方程用SAS9.0中的GENMOD模块来实现。

表1 变量赋值情况
结 果
1.一般情况 共发放问卷600人,实际调查570人,有效应答率95%。其中男性290人,占50.88%,女性280人,占49.12%。年龄 <40岁的31人,占5.44%,40~49岁的53人,占9.30%,50~59岁的139人,占24.36%,60~69岁的189人,占33.16%,≥70岁的158人,占27.72%。570名糖尿病患者中,有170人患有并发症,占总调查患者人数的29.8%,其中患有心脑血管和神经病变的并发症人数分别占调查人数的12.8%和12.5%,各种类型并发症发生情况见表2。

表2 570例糖尿病患者并发症发生情况
2.广义估计方程的分析结果
(1)单因素分析
以并发症发生情况为应变量,患者的年龄、性别、文化程度、患病时间、吸烟、饮酒、体质量指数(BM I)、规律用药情况、血糖、锻炼情况和压力等为自变量拟合广义估计方程,采用无结构的作业作相关矩阵,单因素分析发现文化程度、患病时间、吸烟、饮酒、体质量指数、规律用药情况、血糖、锻炼情况、压力和是否将您了解的预防糖尿病并发症知识付之行动对糖尿病并发症发生的影响差异有统计学意义,详见表3。
(2)多因素分析
对单因素分析结果有统计学意义的变量进行共线性诊断,结果方差扩大因子均小于10,条件指数均小于30,提示这些自变量不存在共线性。以7种并发症发生情况为应变量,患者的文化程度、患病时间、吸烟、饮酒、体质量指数(BM I)、规律服药情况、血糖、锻炼情况和压力等为自变量拟合广义估计方程,采用无结 构的作业相关矩阵,多因素分析结果见表4。
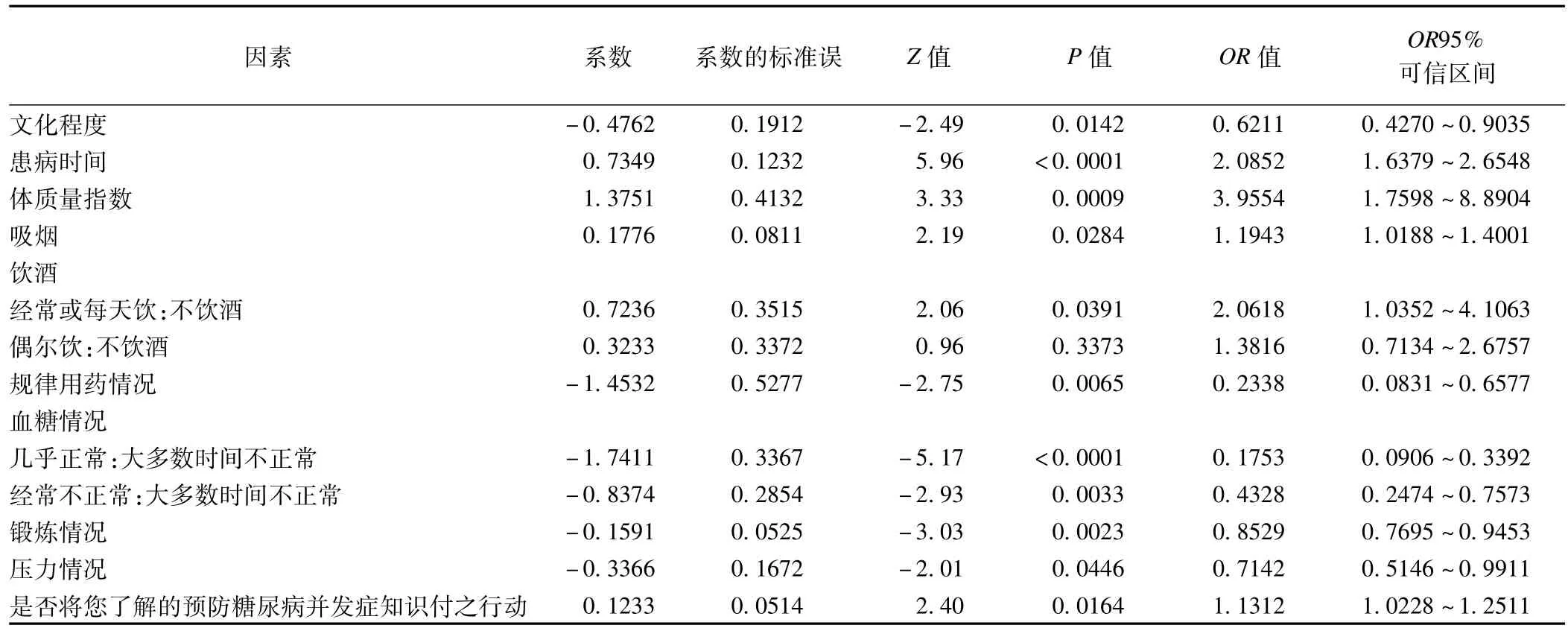
表3 单因素广义估计方程分析结果
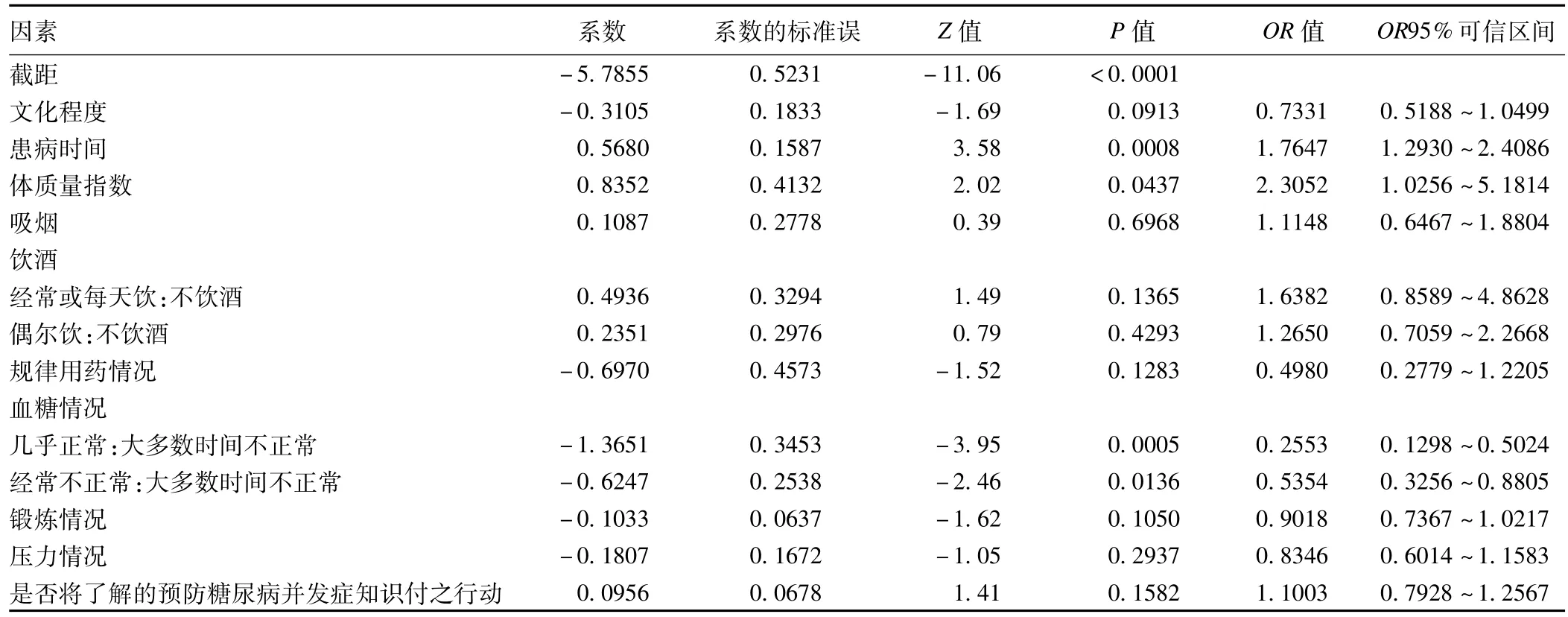
表4 多因素广义估计方程分析结果
在对影响因素各参数估计和假设检验中,患病年限长、体质量指数大、血糖不正常的糖尿病患者更容易出现并发症,文化程度、是否锻炼、压力情况、是否将了解的预防糖尿病并发症知识付之行动和规律用药对并发症的影响无统计学意义。
(3)作业相关矩阵
7类并发症间的作业相关矩阵见表5,说明大多数并发症的发生存在一定的正相关关系即发生一种并发症的患者更容易发生其他并发症。
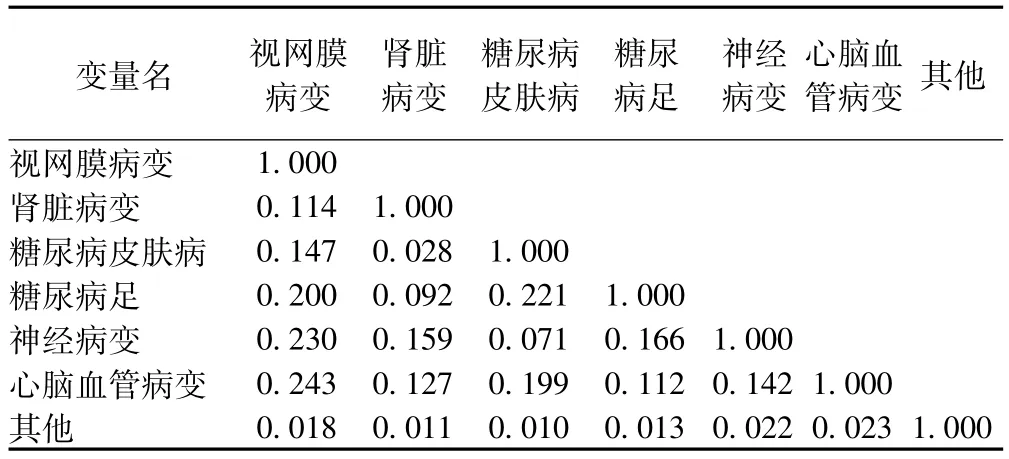
表5 广义估计方程的作业相关矩阵
讨 论
在医学研究中,经常会遇见疾病多种结局数据的分析,这类数据与一般资料不同,它的应变量之间存在相关关系,若采用传统的统计分析方法会忽略数据内部的相关性,低估模型参数的标准误,从而高估检验统计量,使得统计结果出现偏差[3]。广义估计方程突破了广义线性模型“独立性”条件,解决了数据中应变量相关的问题,能得到稳健的参数估计值。
广义线性模型与经典的线性模型相比虽然不要求应变量服从正态分布、应变量与自变量呈线性关系,但它无法解决多个因变量的问题。混合线性模型虽然能解决多个相关性应变量的问题,但要求应变量服从正态分布且应变量与自变量呈线性关系,当应变量是两分类或多分类定性变量时就不适用了。目前国内对多个相关定性应变量的分析方法为多水平模型和广义估计方程,在弱相关和小样本时,广义估计方程比多水平模型稳定[5,7-10]。
一般认为在广义估计方程中只要连接函数选择正确,即使作业相关矩阵的选择不正确,也可以得到稳定的参数估计值[11]。然而,Fitzmaurice的研究结果显示,在模型包含的协变量随时间变化时,若对作业相关矩阵的指定不正确,模型参数估计的效能将降低40%左右[12]。因此,根据实际情况选择合适的作业相关矩阵是比较关键的环节。一般来说,当1水平单位数较少且相等的平衡完全设计资料,推荐采用无结构的作业相关矩阵;对重复测量等具有时间顺序的资料,使用与时间相关的作业相关矩阵;对于整群抽样等资料,测量值间无逻辑顺序关系,建议采用等相关结构的相关矩阵;如果难以确定相关结构,可采用无结构的作业工作相关矩阵。本研究数据属最后一种情形,故采用无结构的作业相关矩阵[3,5]。
本研究发现血糖异常、体质量指数和患病时间是并发症发生的主要影响因素。这与目前于世鹏等人的研究结果一致[13-15],这提示采用广义估计方程分析多疾病结局资料能取得较为满意的结果。
感谢福建医科大学附属第一医院内分泌科的赵淑好、严孙杰等主任对本次调查给予的指导和帮助。
[1]范丽霞.2型糖尿病患者慢性并发症特点及影响因素.中国医院现代远程教育,2012,10(3):17-18.
[2]彭宇辉.二型糖尿病血管并发症的影响因素分析.福州:福建医科大学,2007.
[3]饶克勤主编.卫生统计方法与应用进展(第二卷).北京:人民卫生出版,2008:53-170.
[4]钱荣立.关于糖尿病的新诊断标准及分型.中国糖尿病杂志,2008,8(1):5-6.
[5]万崇华,罗家洪主编.高级医学统计学.北京:科学出版社,2014:235-369.
[6]洪荣涛,曹卫华,欧剑鸣,等.多重应答资料统计分析及其SAS软件实现过程.中国卫生统计,2009,26(6):595-598.
[7]冯国双,罗凤基主编.医学案例统计分析及SAS应用.北京:北京大学医学出版社,2011:222-253.
[8]张华君,闵捷.广义估计方程与多水平模型在相关资料中的比较研究.中国卫生统计,2012,31(1):123-125.
[9]柳青.中华医学统计百科全书多元统计分册.北京:中国统计出版社,2013.
[10]毛广运,沈恬,陈常中,等.广义估计方程在多元统计分析中的运用及检验效率评价.中国卫生统计,2014,31(1):123-125.
[11]张文彤,田晓燕.基于广义估计方程的多重应答资料统计分析方法.中国卫生统计,2004,21(3):139-141.
[12]Fitzmaurice GM.A caveat concerning independence estimating equations with multivariate binary data.Biometrics.1995,51(1):309-317.
[13]于世鹏,班博,孙琳,等.二级预防对糖尿病高血压患者发生大血管并发症的影响.中国临床康复,2006,10(24):4-6.
[14]周春来,丘霞.不同体重指数对初发2型糖尿病并发症及治疗方案的影响.中国医药导报,2014,11(27):58-61.
[15]张威.糖尿病并发心血管疾病的影响因素.实用心脑肺血管病杂志,2008,16(7):11-12.
The Application of Generalized Estimating Equations in the Research about Influencing Factors of Complications of Diabetes Mellitus
Wu Bin,Cao Jianping,Zhou Huangxiu,et al(Department of Epidemiology and Health Statistics,Fujian Medical University(350004),Fuzhou)
ObjectiveTo investigate the application of generalized estimating equations in the research about influencing factors of complications of diabetesmellitus.MethodsThe basic situation,disease and treatment of 570 diabetesmellitus patients were surveyed and the data were analyzed by generalized estimating equations to select risk factors of diabetesmellitus complications.ResultsDuration of disease,body mass index,blood sugar levels are the main factors affecting DM complications.ConclusionGeneralized estimating equation can analyze influencing factors of various outcomes of disease.
Generalized estimating equations;Diabetesmellitus;Complications;Influencing factors
全国统计科学研究计划项目(2012LY169);福建医科大学基金项目(2014JY029S)
1.福建医科大学流行病与卫生统计系(350001)
2.福建医科大学卫生管理系
3.福建省疾控中心健康教育科
(责任编辑:郭海强)

