常用生存分析模型及其对时依性协变量效应的估计方法*
肖媛媛 许传志 赵耐青
常用生存分析模型及其对时依性协变量效应的估计方法*
肖媛媛1许传志1赵耐青2△
生存分析是利用统计学相关理论和方法探索研究因素与“事件时间”(time-to-event)关联的问题。自20世纪50年代其研究方法初具规模以来,经过几十年、尤其是近三十年来的蓬勃发展,生存分析已经成为现代统计学的一个重要分支,研究领域广泛涉及医学、生物学、工程学、经济学及人口统计学等[1]。按照理论基础的不同,和很多统计推断方法一样,自诞生之初起,生存分析也沿着频率法(frequentistmethod)和贝叶斯法(Bayesian method)两条道路分别演进,但发展速度和轨迹存在较大差别。
在贝叶斯生存分析方法中,由似然函数(likelihood function)和参数的先验分布(prior distribution)所共同构建的后验分布(posterior distribution)的表达式往往比较复杂,涉及高维重积分的运算,因此在计算机技术欠发达的年代,这一类生存分析方法的发展几近停滞。20世纪80年代,有学者陆续提出了一些简化后验分布密度及各阶矩计算的近似算法,如Lindley数值逼近法、Naylor-Smith逼近法、Tierney-Kadane逼近法等[2-4],但这些算法的实现仍涉及十分复杂的近似求解技术。直到2000年以后,随着计算机技术的发展和贝叶斯方法的改进,特别是马尔科夫链蒙特卡洛法(Markov Chain Monte Carlo,MCMC)的成功运用后[5-6],贝叶斯生存分析法才真正开始快速发展。尽管如此,与其他任何贝叶斯统计推断方法一样,如何准确定义先验分布的问题仍然是限制其进一步发展的最大阻碍。由于贝叶斯生存分析法在实际运用中需要较为精深的数理统计理论知识作为支撑,其推广运用必然受限。基于上述背景,本文将不再讨论这一类生存分析方法,而将重点放在常用的频率生存分析法上。
与贝叶斯生存分析法不同,频率生存分析法严格忠于数据本身,因此不会遭受“客观性”的质疑。此外,其理论基础没有贝叶斯法抽象晦涩,计算方法也较贝叶斯法简便得多。因此,不论是在当前的生存分析模型的方法学研究领域,还是在具体生存模型的运用领域,频率生存分析法都占绝对主导地位。按照算法或模型的架构是否依赖特定参数分布,频率生存分析法分为非参数法(non-parametric method)、半参数法(semi-parametric method)和参数法(parametric method)三类。
在研究某一因素与生存时间的关联时,这一因素的取值或分类可以是恒定不变的,也可以是呈一定规律或无规律变化的。另外,该因素对结局变量的效应也可能随时间发生变化,这一类因素可被统称为时依性协变量(time-dependent covariates)。以医学研究为例,性别、种族、成年人身高等因素可以认为在一定研究时期内保持不变,而各类血液化验指标、体重、血压等体格测量指标则很可能是不断变化的。要评价这些变动的因素对生存时间的影响,必须将其变动的信息充分利用起来,才能得到更为准确的结论。绝大多数经典生存分析模型在提出之初都可以看作是“静态生存分析模型”,因为为了简化理论推导,一般都会给出协变量取值及对结局变量效应恒定的假设。在其后的运用中,再根据协变量的变动规律或近似变动规律对原始“静态生存分析模型”进行拓展,形成各类“动态生存分析模型”。以Cox比例风险模型为例,在原始模型提出之后,Kalbfleisch和 Prentice[7],以及 Cox本人和Oakes[8]就对该模型进行了改良,特别是讨论了时依性协变量的分析方法,大大提升了原始模型的实际应用价值。时至今日,时依性协变量的分析方法在多类生存分析模型中均有涉及,本文将对常用生存分析方法及其对时依性协变量的效应估计做简要梳理。
非参数法
1.常用方法
非参数生存分析方法在理论架构上有共性,即:不使用原始数据中生存时间分布及具体时间长短等信息,而仅仅利用不同个体生存时间的秩次排序。最常见的非参数生存分析法有用以描述生存时间分布的乘积极限法(product limit method),也称作 Kaplain-Meier法[9],以及比较两组或多组生存时间差异的一组非参数检验,如对数秩检验(log-rank test)、Wilcoxon检验及 Mantel-Haenszel检验[7,10-11]。
(1)Kaplain-Meier法
假设在一组观察对象中,到观察结束时,一共有m个个体在j个时间点发生了死亡(或其他任何所研究的结局事件,下文均以死亡为例),且死亡时间点的排序为:0≤t(1)≤t(2)…≤t(j)≤∞。假设恰好在某个特定死亡时间点t(j)之前,仍有 r(j)个观察对象有死亡风险(意味着仍然存活且未发生截尾),而在t(j)时间发生了d(j)例死亡,则据此可估算t时刻的生存函数值为:
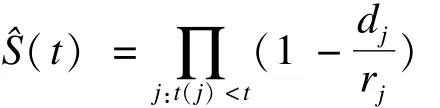
这一取值也被称作K-M估计值(K-M estimator)。不难看出,K-M估计值从定义来看在时间维度上应该是一个离散函数。如假设所有死亡事件均恰好发生在死亡时点,而两个离散的死亡时点间无死亡发生,则可根据K-M估计值将生存曲线绘制为连续的、逐步递减的阶梯函数(step function),只在发生死亡的时点变化数值。对于离散时点来说,可以证得K-M估计值实际上也是最大似然估计值(maximum likelihood estimate)[8]。
K-M估计值可被证明服从近似正态分布[12-13],因此可以计算其可信区间。Greenwood提出了计算其可信区间的近似公式(Greenwood′s formula)[14]:
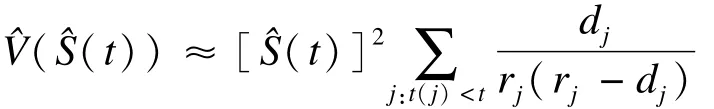
这一公式也可用来计算百分位数生存时间的可信区间。
(2)以秩次为基础的非参数检验
对数秩检验、Wilcoxon检验及Mantel-Haenszel均是以秩次为基础的非参数检验。考虑其原理的大同小异,只简略介绍最为常见的对数秩检验。
对数秩检验的基本思想为:假设有两组观察对象,将观察时间内两组发生的所有死亡个体提出,按照死亡时间从短到长混合排序0≤t(1)≤t(2)…≤t(j)≤∞。假设t(j)之前,两组加在一起一共有 r(j)个对象有死亡风险,其中第一组有 r(1j)个,第二组有 r(2j)个。t(j)这一时刻一共发生了 d(j)例死亡,其中第一组 d(1j)例,第二组 d(2j)例。在无效假设成立的背景下,任意时刻发生死亡的风险在两组间应相同(只存在随机抽样误差),因此可以用在任意时刻的死亡风险 d(j)/r(j)来估算第一组的期望死亡数(e1j),并用每一时刻期望死亡数和观测死亡数(d1j)的差值构建检验统计量UL:
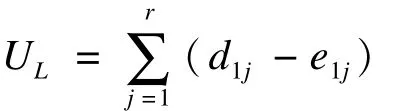
在每一死亡时点上,每一组死亡数均服从参数为r(j)和 d(j)的超几何分布(hypergeometric distribution),据此可计算得到UL的方差为:
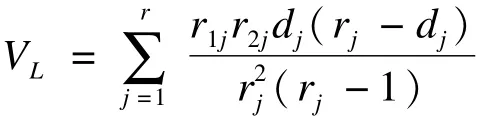
在无效假设成立的条件下,UL服从正态近似分布N(0,VL),即可参照正态分布做出统计推断。
Mantel-Haenszel检验与对数秩检验的主要差别只体现在,其检验统计量值和方差均为对数秩检验统计量和方差的平方,因此依据卡方分布做出统计推断。而Wilcoxon检验与对数秩检验的区别是,其计算检验统计量及其方差时乘以每一时刻存活病人总数(r(j))作为权重。近年来,国内有学者讨论了无删失存在时Wilcoxon检验与对数秩检验的I型错误率和检验效能,模拟结果表明两法存在一定差别[15]。
2.对时依性协变量效应的估计
K-M法一般用来绘制生存时间分布较多,而基于秩次的几种非参数检验常用来初步比较单个分类变量或少数几个分类变量的联合分布对生存时间的影响。一旦分类变量数量较多且每个变量分类较多,由于分层后数据过于稀疏,其检验效能往往会大打折扣。此外,更是无法分析连续性变量对生存时间的影响。在如此多的固有缺陷下,想要处理时依性协变量就显得更不实际了。在未限定发表时间,以三个关键词“nonparametric”、“survival analysis”、“time dependent”组合检索Web of Science后,经过标题和摘要筛选,我们只寻找到了一篇切题文献,但经过全文阅读后,发现作者采用的方法并非严格意义的非参数法,而是半参数法[16]。
半参数法
1.常用方法
(1)半参数比例风险模型(Cox proportional hazards model)
比例风险模型的构建满足如下假设:在基础风险和其他协变量固定不变的前提下,某一协变量取值每增加一个单位,得到的风险函数的取值等于原来的风险函数取值乘以一个固定系数。其表达式十分简洁:

上式中,h0(t)是基础风险函数。在半参数比例风险模型中,对基础风险函数(baseline hazard function)不做任何限定,只是对各研究因素(x1~xp)对基础风险的作用做出参数限定(βT)。这也是“半参数模型”这一名称的由来,这一模型最初是由英国著名统计学家Cox提出的,因此也称作Cox比例风险模型[17]。
由于未限定基础风险函数,也就是未限定生存时间分布,不可能得到概率密度值(考虑生存函数、风险函数、概率密度函数三者间的转化关系,后文将会提及),因此在估计参数时,传统的极大似然法无法使用。Cox采用了一个非常巧妙的处理来化解这个问题,假设每个死亡时点只有一个死亡对象,则其概率密度估算值可用风险函数表示为:
P(i对象在 t(j)时刻死亡|在 t(j)时刻存在风险的R(j)个对象至少有一个死亡)

由于上式分子分母均同样含有t(j)时刻的基础风险,因此可以约除。假设一共有n个死亡事件,则似然函数可表示为:
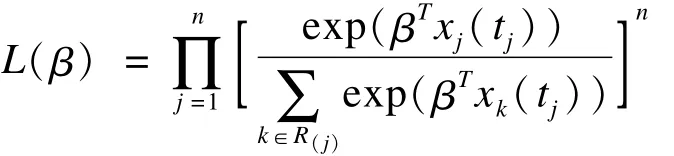
上式的实质是通过风险函数所构建的子集似然函数(profile likelihood function),并不是真正意义上的似然函数。因为不包含所有的未知参数,故也被称作偏似然函数(partial likelihood function)[18]。在偏似然函数中,未作限定的基础风险值已经不存在,不需要对其进行估计。与普通似然函数求极值相似,仍然可通过迭代法(如New ton-Raphson法)寻找其最大值,从而得到β′的极大偏似然估计。
(2)半参数加速失效模型(sem i-parametric accelerated failure timemodel)
加速失效模型是另一类常见的生存分析模型,但其在实际研究中的应用却远没有比例风险模型广泛。加速失效模型的目标函数直接选择为生存时间T,因此较之比例风险模型,其协变量系数的解释更为明确。加速失效模型构建的假设为:在基线生存函数及其他协变量恒定的情况下,某一协变量每增加一个单位,生存时间等于原来的生存时间乘以一个固定系数。
模型的表达式一样不失简洁:

上式中,ε是随机误差,对应基线生存函数的对数。xl~xp是研究对象的协变量取值,a1~ap是协变量的系数。
在半参数加速失效模型中,对基线生存函数的分布未做任何限定,只限定协变量的系数。在满足加速失效模型假设的前提下,风险函数的表达式为:
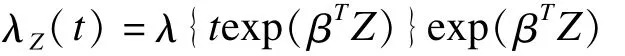
前面提到,在Cox比例风险模型中,虽然一样未限定基线风险函数,但比例风险的假设可以在用风险函数的比值构建偏似然函数时将基线风险顺利约除。而在上式中,误差项exp(ε)的风险函数值λ(·)完全未知。因此无法在半参数加速失效模型中用风险函数如法炮制偏似然函数。正是由于这一限制,参数加速失效模型反而比半参数模型应用更为广泛。不过在过去三十年里,许多统计学家提出了一系列以秩次和最小二乘为基础的半参数加速失效模型参数估计和推断方法,其中比较有代表性的有 Prentice,Buckley和James,Ritov,Tsiatis,Lai和 Ying等[19-24]。除去计算极其复杂之外,这些方法存在一个共同问题,那就是均为离散函数,可能存在多重根,难以对函数值及其方差做出估计。
(3)其他半参数生存分析模型
其他较为常见的半参数生存分析模型还包括比例优势模型(proportional odds model)和相加风险模型(additive hazardsmodel)。其模型表达都比较简洁,但参数估计时所涉及的运算却极具挑战性,在此不做详述。如比例优势模型参数估计的常用方法,是在给出一系列分布限制条件的基础上(从这个意义上说,半参的假定已经被部分违背)构建似然函数,并且该似然函数也只是在进一步的限制条件下才存在最大值[25]。再如相加风险模型,虽然可以顺利构建似然函数,但似然函数的最大值却不存在,而随后提出的一些近似估计方法的表现也差强人意[26-27]。
2.对时依性协变量效应的估计
(1)Cox比例风险模型
在Cox比例风险模型中,目前有两大类处理时依性协变量的方法。第一类不妨称其为“函数法”。其思路很直接:如果一个协变量在生存时间的维度随时间的变化而变化,则可以在原始Cox比例风险模型中加入该变量和时间的交互作用项来描述其变化对基线风险的影响。调整后的风险函数表达式为:

上式中,xj为时依性协变量,其在t时刻的取值为xj(t=0)×g(t)。从该表达式不难看出,在控制了 xj的变化对基础风险的影响之后,其他协变量仍满足比例风险假定。
这种方法的运用需要满足两个前提:一是可以准确找到协变量xj随时间变化的函数关系式g(t)。在实际研究中,一般都是通过获取的数据来寻找变量间的函数关系。当两者关系为一次或者二次函数时,找准关系或许不难。而一旦多次函数出现,在数据本身就夹杂了抽样误差和各类偏倚的情况下,准确定位其函数关系显然无法实现。二是协变量xj每改变一个单位,对基础风险的影响保持恒定不变。这同样是一个极强的假设,以医学研究为例,往往某一指标发生变化后,其作用机理也会发生改变,由此导致效应强度发生变化。
另一种处理方法是借鉴counting process法的思路调整生存数据后,再运用Cox模型进行分析,并在模型参数估计的时候运用多结局生存分析的思路校正观测间的组内相关性。生存分析中有着广泛应用的counting process法是由 Fleming和 Harrington[28]于 20世纪90年代初在Aalen[29]的研究基础上发展成熟的。这一方法给生存分析理论的拓展带来了极大推进,如基于counting process法计算得到的鞅残差(martingale residual)估计值可以作为模型拟合的评判标准,再如运用鞅论的相关公理,可证得协变量系数的极大似然估计值服从近似正态分布,且其协方差矩阵可以从观测到的信息矩阵(information matrix)中估计获得[30]。这里提到的方法,仅仅是借鉴了counting process的思路来重构生存数据,并不实际运用原方法,为了加以区别,不妨称其为“多结局counting process法”。
多结局counting process法重构生存数据的基本思想是:假设变动的因素为x,研究对象A结局事件发生时间为t(d),在结局事件发生前,一共随访了3次(t(1)<t(2)<t(3)<t(d)),每次测得 x的取值分别为 x(1),x(2)和 x(3)。假设 x(1)=x(2)≠x(3)。由此可知研究因素x取值在t(3)发生了变化,则以t(3)为分界点,将原来数据集中研究对象A所对应的一条记录(t(d),1)(数据结构为(T,C),其中 T代表随访时间,C是指示变量,1代表死亡,0代表删失),裂解为新生存数据集中的两条记录(t(1),t(3),0)和(t(3),t(d),1)(数据结构为(T(1),T(2),C),其中 T(1)是随访开始时点,T(2)为随访结束时点,C是指示变量,1代表死亡,0代表删失)。如此一来,每个研究对象从原始生存数据集中的一条记录变为新生存数据集中的一组记录,可以视为同一研究对象的多结局事件。
在重构的新生存数据集中,每一条记录所对应的x为恒定取值,因此可根据不同假设采用Cox比例风险模型进行参数估计。常见的假设有两种,一是假设各随访开始时点(T(1))的基线风险均相同,最后得到研究因素的唯一效应估计值;二是假设各随访开始时点的基线风险不相同,最后得到的是不同时刻研究因素效应的一组估计值。在进行参数可信区间估计时,考虑到新生存数据集中来自同一个观察对象的多条记录存在内部相关,采用“夹心方差估计”(sandw ich variance estimator)调整方差[31-34]。
虽然多结局counting process法在应用时也有较强的假设作为前提,最为突出的一点就是假设每个研究对象的各个“结局”间互相独立。但较之前述及的“函数法”,显然灵活和强大得多。在完成数据结构调整后,分析方法与传统Cox比例风险模型相同,仅仅需要额外调整组内相关性。因此采用常用统计分析软件(如SAS或R)的生存分析模块即可轻松实现,具体操作方法和程序编码目前也有相关文献可供参考[35-36]。
(2)半参数加速失效模型
前面已经提到,在估计恒定不变的协变量的效应时,以秩次和最小二乘为基础的参数估计方法所涉及的计算已经极其复杂且表现不佳,在此基础上,不可能再将时依性协变量整合其中。直到2007年,Zeng和Lin提出了一个在半参数加速失效模型中估计时依性协变量效应的可行方法[37]。他们首先将时依性变量整合进半参数加速失效模型中,得到:
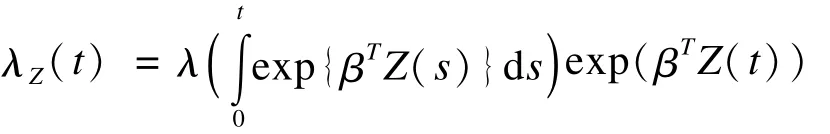
上式中,λ(·)是误差项exp(ε)的未知基线风险函数,同样,偏似然函数仍无法构建。他们提出了采用核平滑(kernel smoothing)来构建子集似然函数的平滑近似函数,再以此平滑近似函数为基础进行参数估计。随后的数据模拟发现,据此方法得到的近似估计值较为准确和稳定。虽然这一方法的提出为半参数加速失效模型中时依性协变量的效应估计提供了可能,但如此复杂的运算显然无法推广应用。
参数法
1.常用方法
参数生存分析模型和半参数生存分析模型的最大区别在于,限定生存函数(survival function,S(t))满足一定概率分布,由此,风险函数(hazard function,h(t))及结局事件概率密度函数(probability density function,f(t))也相应确定。因为三个函数满足以下转换关系:

目前常用的参数生存分析模型分为两大类:比例风险模型和加速失效模型。
(1)参数比例风险模型(parametric proportional hazards model)
参数比例风险模型和半参数的Cox比例风险模型在表达式上基本相同:

唯一的区别为:参数比例风险模型假设基础风险h0(t)满足一定的概率分布。可以看出,该模型仍然假设协变量对基础风险的改变等于固定的乘积比例。满足“比例风险”这一理论假设的生存分布有指数分布(exponential distribution)、韦伯分布(Weibull distribution)和 Gompertz分布(Gompertz distribution),因此参数比例风险模型也分为这三种。
一旦生存分布选定,即可根据生存函数和概率密度函数之间的转换关系,构建似然函数,得到模型参数的极大似然估计。
(2)参数加速失效模型(parametric accelerated failure time model)
参数加速失效模型与半参数加速失效模型的本质区别也在于限定了基线生存函数的分布,即函数表达式中εi项的分布。其表达式为:
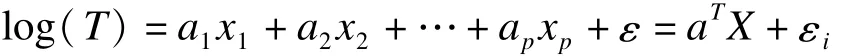
满足加速失效模型假设的生存函数分布类型较满足比例风险假设的分布类型多,有指数分布、韦伯分布、对数-logistic分布(log-logistic distribution)、对数-正态分布(log-normal distribution)和伽马分布(Gamma distribution)。
同样,生存时间分布一旦限定,即可构建似然函数,从而得到模型参数的极大似然估计。
2.对时依性协变量效应的估计
在估计时依性协变量x的效应时,两类参数生存分析模型往往在假设x的单位增量对应变量(风险或生存时间)的效应保持不变、且x遵循一定的随时间变化规律(f(t))的情况下,在原生存分析模型中加入x与f(t)的交互作用项。再以调整后的函数为基础构建似然函数,采用极大似然法得到协变量效应估计值。前面述及的“多结局counting process法”当然也可以顺利应用于参数生存分析模型,但由于Cox模型在实际运用中的巨大优越性,counting process法在参数比例风险模型中的探讨较少。一些学者讨论了其在参数加速失效模型中的运用[38-39]。
可能是由于假设生存分布已知,扫除了生存分析模型参数估计时的理论障碍,目前参数生存模型中针对时依性协变量效应估计的研究并不多。近年来有学者开始讨论在弱假设前提下时依性协变量的效应估计,如Sparling和Hamid等提出了将样条函数(Spline function)整合入参数生存分析模型,并结合不同数据删失类型,估计非线性变化的时依性协变量的效应[40-41]。
总 结
虽然在个别生存分析模型,如半参数加速失效模型中,缺乏可行的时依性协变量效应的估计方法。目前对于大多数常见的半参数和参数生存分析模型来说,借助常用统计分析软件中已有的生存分析模块,可顺利实现对时依性协变量的效应估计。现有研究数量的不足及理论瓶颈决定了时依性协变量效应估计新方法的探索,以及现有方法的简化和拓展将是未来很长一段时期内生存分析方法学研究的重点和难点之一。此外,一些现有复杂算法在常用统计分析软件中的实现也将是统计开发人员需直面的技术挑战。
[1]林静.基于MCMC的贝叶斯生存分析理论及其在可靠性评估中的应用.南京理工大学,2008.
[2]Lindley DV.“Approximate Bayesian methods”in Bayesian statistics.Valencia,Spain:Valencia Press,1980.
[3]Naylor JC,Sm ith AFM.Applications of a method for the efficient computation of posterior distributions.Applied Statistics,1982,31(2):214-225.
[4]Tierney L,Kadane JB.Accurate approximations for posterior moments and marginals.Journal of American Statistical Association,1986,81(1):82-86.
[5]Congdon P.Bayesian statistical modeling.England:John Wiley and Sons,2001.
[6]Congdon P.Applied Bayesian modeling.England:John Wiley and Sons,2003.
[7]Kalbfleisch JD,Prentice RL.The statistical analysis of failure time data.New York:John W iley&Sons,1980.
[8]Cox DR,Oakes D.Analysis of survival data.London:Chapman and Hall,1984.
[9]Kaplan E,Meier P.Nonparametric estimation from incomplete observations.Journal of the American Statistical Association,1958,53(282):457-481.
[10]Mantel N.Evaluation of survival data and two new rank order statistics arising in its consideration.Cancer Chemotherapy Report,1966,50(3):163-170.
[11]Gehan EA.A generalized Wilcoxon test for comparing arbitrarily singly censored samples.Biometrika,1965,52:203-223.
[12]Andersen PK,Borgan O,Gaill RD,et al.Statistical methods based on counting processes.New York:Springer,1993.
[13]Flem ing TR,Harrington DP.Counting processes and survival analysis.New York:John W iley&Sons,1991.
[14]Greenwood M.A report on the natural duration of cancer.Reports on Public Health and Medical Subjects 33.London:HM Stationary Office,1926:1-26.
[15]陈靖,何春拉,潘建红,等.无删失生存数据Wilcoxon秩和检验与logrank检验的比较.中国卫生统计,2012,29(5):654-660.
[16]Zucker DM,Karr AF.Nonparametric survival analysis with time-dependent covariate effects:a penalized partial likelihood approach.The Annals of Statistics,1990,18(1):329-353.
[17]Cox DR.Regression models and life-tables.Journal of the Royal Statistical Society.Series B,1972,34(2):187-220.
[18]Cox DR.Partial likelihood.Biometrika,1975,62(2):269-276.
[19]徐英,骆福添.Buckley-James模型在生存分析中的应用.中国卫生统计,2007,24(1):69-70.
[20]Prentice RL.Linear rank tests with right-censored data.Biometrika,1978,65(1),167-179.
[21]Buckley J,James I.Linear regression with censored data.Biometrika,1979,66(3),429-436.
[22]Ritov Y.Estimation in a linear regression model with censored data.The Annals of Statistics,1990,18(1),303-328.
[23]Tsiatis AA.Estimating regression parameters using linear rank tests for censored data.The Annals of Statistics,1990,18(1),354-372.
[24]Lai TL,Ying Z.Rank regression methods for left-truncated and right censored data.The Annals of Statistics,1991,19(2),531-556.
[25]Murphy SA,Rossini AJ,Van der Vaart AW.Maximum likelihood estimation in the proportional oddsmodel.Journal of the American Statistical Association,1997,92(439):968-976.
[26]Lin DY,Ying Z.Semiparametric analysis of the additive riskmodel.Biometrika,1994,81(1):61-71.
[27]Zeng D,Cai J.Asymptotic results for maximum likelihood estimates in joint analysis of repeated measurements and survival time.The Annals of Statistics,2005,33(5):2132-2163.
[28]Flem ing TR,Harrington DP.Counting process and survival analysis.New York:John W iley&Sons,1991.
[29]Aalen O.Nonparametric inference for a family of counting processes.The Annals of Statistics,1978,6(4):701-726.
[30]Hosmer DW,Lemeshow S,May S.Applied survival analysis:regression modeling of time-to-event data,Second Edition.New York:John Wiley&Sons,2008.
[31]高峻,董伟,高尔升,等.多结局生存分析模型与Cox模型的随机模拟比较.中国卫生统计,2007,24(3):248-254.
[32]Kelly PJ,Lim LL.Survival analysis for recurrentevent data:an application to childhood infectious disease.Statistics in Medicine,2000,19(1):13-33.
[33]Eric WL,Wei LJ,Amato DA,et al.Cox-type regression analyses for large numbers of small groups of correlated failure time observations.Survival analysis:state of the art.Netherlands:Springer Netherlands,1992:237-247.
[34]Finkelstein DM,Schoenfeld DA,Stamenovic E.Analysis of multiple failure time data from an AIDS clinical trial.Statistics in Medicine,1997,16(8):951-961.
[35]Thomas L,Reyes EM.Tutorial:survival estimation for Cox regression models with time-varying coefficients using SAS and R.Journal of Statistical Software,2014,61:1-23.
[36]Powell TM,Bagnell ME.Your“survival”guide to using time-dependent covariates.SASGlobal Forum,2012:168.
[37]Zeng D,Lin DY.Efficient estimation for the accelerated failure time model.Journal of the American Statistical Association,2007,102(480):1387-1396.
[38]Lin DY,Wei LJ.Accelerated failure time models for counting processes.Biometrika,1998,85(3):605-618.
[39]Huang Y,Peng L.Accelerated recurrence time models.Scandinavian Journal of Statistics,2009,36(4):636-648.
[40]Sparling YH,Younes N,Lachin JM.Parametric survival models for interval-censored data with time-dependent covariates.Biostatistics,2006,7(4):599-614.
[41]Ham id HA.Flexible parametric survival models with time-dependent covariates for right censored data.University of Southampton,2012.
国家自然科学基金(81460519,H2611);云南省自然科学基金(2013FZ064)
1.昆明医科大学公共卫生学院流行病与卫生统计学系(650500)
2.复旦大学公共卫生学院生物统计学教研室
△通信作者:赵耐青,E-mail:nqzhao1954@163.com
(责任编辑:郭海强)

