基于时变波动率与混合对数正态分布的50ETF期权定价
王 鹏,杨兴林
西南财经大学 中国金融研究中心,成都 611130
基于时变波动率与混合对数正态分布的50ETF期权定价
王 鹏,杨兴林
西南财经大学 中国金融研究中心,成都 611130
经典B-S期权定价模型经历了从常数波动率、正态分布到时变波动率、非正态分布的发展历程。
对已有针对时变波动率期权定价模型效果的研究进行扩展,以时变波动率模型SSP对经典B-S期权定价公式的常数波动率进行修正,该随机条件波动率的构建充分反映了未来标的资产收益对其波动率的影响;运用广义学生t分布构建时变波动率调整后的B-S期权定价公式,并研究其风险中性概率分布形状,引入混合对数正态模型捕捉实际收益率分布相对于正态收益率分布的偏离;采用2015年2月9日、2月16日和2月25日的50ETF期权高频数据,应用严谨的参数显著性检验、样本内定价偏差和样本外预测偏差的模型选择比较标准,对提出的具有时变波动率的混合对数正态期权定价模型的定价精度进行分析。
研究结果表明,中国50ETF期权的标的资产高频收益率呈现出较为明显的有偏和尖峰厚尾分布,收益波动具有明显的聚集特征和长记忆性;采用时变波动率修正后的B-S模型能够显著提高对中国50ETF期权的定价精度;在综合考虑模型对标的资产价格变化动力学的刻画效果以及对期权的定价精确性后,具有时变波动性特征的混合对数正态模型是一个相对更为合理的期权定价模型。
研究结果不仅为投资者和监管机构提供了更为准确的期权定价方法,同时也丰富了有关中国50ETF期权典型统计特征的研究。
混合对数正态分布;时变波动率;Black-Scholes模型;期权定价;50ETF
1 引言
近年来,对期权定价的研究是现代金融理论的重要内容之一,期权作为一种衍生性金融工具,对于活跃金融市场、完善金融市场价格发现功能具有重要意义。因此,对期权进行精确定价不仅直接影响到机构投资者和个人投资者的投资策略,而且还可以为金融监管当局提供相关决策的信息支持。与此同时,标志着中国正式拥有了全套主流金融衍生产品的50ETF期权的成功上市,使中国监管机构、做市商和投资者等对于期权的定价精度的要求提高,因此,对于如何改善期权定价模型的定价精度的相关研究具有实践意义。
2 相关研究评述
在已有研究中,由于BLACK et al.[1]提出的经典B-S模型逻辑严密、形式优美、涉及变量较少及计算相对简便,被理论界和实务界广泛用于为衍生品定价[2-4]。但是,由于经典B-S模型的假设条件中存在若干与实际市场运行特征不符之处,如现实中存在的金融资产(经验)收益率的时变波动性[5-7]和其非正态性[8-10]说明经典B-S模型常数波动率和正态分布的假设有误,因此学者们在经典B-S模型上进行了许多有意义的改进[11-12]。
首先,由于波动率是对标的资产风险的二阶矩刻画且也是期权定价建模的重要组成部分,因此对经典B-S模型的常数波动率假设进行修正成为金融实务界关注的热点。CHRISTOFFERSEN et al.[13]和BYUN et al.[14]对期权的标的资产收益率采用GARCH波动率建模,构建风险中性估值模型,并发现GARCH波动率模型比经典B-S模型中的常数波动率模型能够更好地解释已被充分证实存在的系统性偏差; CHRISTOFFERSEN et al.[15]和CORSI et al.[16]采用高频数据构建实现波动率模型,发现得到的随机波动率期权定价模型具有更好的定价效果;CHEN et al.[17]和ALS et al.[18]通过构建隐含波动率模型实现对标的资产收益率的波动预测,进而取得了更好的期权定价效果。中国也有许多关于常数波动率修正的有价值的研究[19-21]。
其次,许多学者对于标的资产收益率分布的非正态性展开研究,取得了许多有价值的成果。赵攀等[22]提出Tsallis分布的欧式期权定价模型,并在对上证指数数据实证分析中发现Tsallis分布对资产收益率尖峰厚尾及偏尾等现象的捕捉更为精确;KIM et al.[23]和HUANG et al.[24]认为广义极值分布和广义的Logistic分布更能准确地刻画标的资产收益率厚尾特征,通过对标准普尔500指数期权实证研究,发现这些分布可以让修正后的经典B-S模型具有更好的灵活性和实用性;JIMÉNEZ et al.[25]和MOSCOSO et al.[26]研究发现广义Tukey分布由于考虑了标的资产收益率的偏度和峰度,更能准确描述标的资产收益率的分布特征,使在该分布修正下的经典B-S模型具有更高的定价精度。
另外,也有学者从其他视角对期权定价进行了研究,为后续改善期权定价精度的研究提供了新的渠道和方法。FRY-MCKIBBIN et al.[27]认为在金融危机时期外汇期权的定价会出现比较严重的偏差,降低了风险对冲效率,这是由于没能将刻画市场之间的风险传染的协偏度考虑进传统的期权定价模型中;RECCHIONI et al.[28]在雷曼兄弟倒闭和欧债主权债务危机发生导致美国和欧元区负的政府债券收益率的大背景下,通过构建负利率的期权定价模型,实证发现该模型在负利率出现时具有更好的定价精度和波动率预测效果;传统的期权定价模型很少考虑市场流动性的冲击对期权买卖价差的影响,LEIPPOLD et al.[29]考虑市场流动构建了随机流动性模型,并结合多维二叉树方法成功地对标准普尔500指数看涨和看跌期权进行了校准。
尽管对于期权定价的研究已经取得了很多有价值的成果,但大多数研究要么集中于对常数波动率假设的单方面修正[30-32],要么仅对资产价格分布进行重新刻画[22,33-34],还很少见到同时对常数波动率和正态分布进行修正以提高期权定价精度的系统性研究。另外,中国专门针对上证50ETF期权定价的研究成果较少,杨瑞杰[35]在上证50ETF期权推出后,对期权交易能否提高标的资产定价效率进行了研究。
本研究同时修正了经典B-S模型中标的资产收益率为常数波动率和标的资产收益率服从正态分布这两大与实际市场运行特征不符的核心假设。①ROSENBERG et al.[36-37]提出的条件方差方程式能够准确地度量方差对于对数正态分布的偏离以及反映金融资产收益率的时变波动性特征,因此采用ROSENBERG et al.[36-37]提出的条件方差方程式和LYE et al.[38]提出的灵活参数分布构建具有时变波动性特征的B-S模型;②MELICK et al.[39]提出的混合对数正态分布相较于正态分布也能更好地刻画标的资产收益率分布偏度、峰度和多峰等特征,因而引入MELICK et al.[39]提出的混合对数正态分布构建具有时变波动性特征的混合对数正态模型;③以上证50ETF期权为实证研究对象,考察并比较本研究构建的具有时变波动性特征的B-S模型与具有时变波动性特征的混合对数正态模型的定价精度,进而得到更为合理的看涨期权定价模型。
3 理论介绍和模型构建
3.1 时变波动率的理论介绍
由于经典B-S模型下的分布密度函数对于实际收益率分布的刻画往往具有很大的偏离,因而ROSENBERG et al.[36-37]采用著名的Sigma形状多项式(Sigma shape polynomial,SSP)对这一缺陷进行修正,表达式为
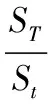
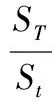
(1)
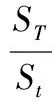
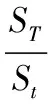
(2)
随后,LIM et al.[40]在对S&P 500指数期权进行高阶矩参数期权定价时也构建了SSP变形形式,即
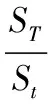
(3)
基于上述研究发现,对于SSP模型只用到总收益对数项就能充分反映金融资产(经验)收益率的时变波动性特征,并能充分捕捉对数正态分布对于实际分布的偏离。因此,本研究构建的期权定价模型均采用(3)式的条件波动率。
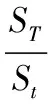
与建立在滞后收益上的GARCH类时变波动率模型相比,(3)式具有许多优势。首先,体现了期权价格的决定与标的资产未来价格变化的联系;其次,所有随机性都源自于资产价格本身的随机性,没有额外的残差项产生;最后,计算相对简便。
3.2 构建具有时变波动性特征的B-S模型
在对期权鞅定价的研究中,INGERSOLL[41]和HULL[42]认为对于一份t时刻欧式看涨期权估值的核心思想是风险中性条件下的均值现金流贴现,即
F(St)=EQ[e-rτmax(ST-X,0)|St]
(4)
其中,F(St)为在EQ[·|St]下的理论期权价格,EQ[·|St]为风险中性概率测度,r为每日的无风险利率,τ为期权的到期天数,X为期权的执行价格。变换(4)式可得风险中性概率分布的广义形式,即

(5)
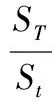
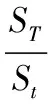
(6)
其中,zT为均值为0、方差为1的标准随机变量。
LYE et al.[38]认为,广义学生t分布的特点是具有很强的参数灵活性,能够通过参数赋值得到正态、学生t等各种分布。广义学生t分布具有的高阶矩项也为刻画标的资产收益率构建更为复杂的分布创造了条件。本研究仅选取广义学生t分布经参数赋值后得到的正态分布进行研究,通过此分布重构具有时变波动性特征的经典B-S模型。本研究重构具有时变波动性特征的经典B-S模型,步骤如下。
(1)假设(6)式中的标准随机变量zT服从LYE et al.[38]提出的广义学生t分布,进而根据LIM et al.[40]所构建的一般随机变量在广义学生t分布下的概率密度函数得到本研究构建模型所需的标准随机变量zT的概率密度函数,即
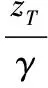
-∞ (7) 其中,θ1~θ6、γ为参数,θ1~θ6刻画了标准随机变量zT的不同分布形状,γ的平方项为自由度;k为积分常数,具体形式为 (8) p(zT)=ke-0.5z2T (9) (2)运用p(zT)求风险中性概率密度g(ST|St),即 g(ST|St)=|J|p(zT) (10) 其中,J为能够实现从现实测度(P测度)到风险中性测度(Q测度)的雅可比行列式,即 (11) 将(10)式代入(11)式得到风险中性概率密度,即 (12) (3)将本研究构建的风险中性概率密度(12)式代入(5)式,得到在风险中性概率测度下具有时变波动性特征的B-S模型(简记为Normal),即 F(St)=BS(σT|t) (13) (4)进一步假定(3)式中的β2=0,可以得到波动率为常数的风险中性概率密度,即 (14) 将在常数波动率下的风险中性概率函数代入(5)式,得到波动率为常数的经典B-S模型,即 F(St)=BS(σ)=StN(d1)-Xe-rtN(d2) (15) 其中,σ为经典B-S模型假设下的常数波动率,σ=exp (β1)。d1和d2的具体形式为 (16) 由于众多实证研究结果表明金融资产(经验)收益率并不服从正态分布,而是具有偏态、厚尾等典型特征。因此,本研究采用MELICK et al.[39]提出的能够准确刻画真实分布的混合对数正态分布,通过该分布构建具有时变波动性特征的混合对数模型,对经过时变波动率修正后的B-S模型(即(13)式)进一步改进。 (1)混合对数正态分布模型在常数波动率下的定价方程式为 F(St)=αBS(σ1)+(1-α)BS(σ2) 0<α<1 (17) 其中,BS(σi)为常数波动率下的经典B-S模型,具体表达形式如(15)式所示,i=1,2;α为衡量下属两个对数正态分布的权重参数。 (2)运用(3)式构建的时变波动率对(17)式中的常数波动率进行调整,得到时变波动率调整后的混合对数模型(简记为Mixture),即 F(St)=αBS(σ1,T|t)+(1-α)BS(σ2,T|t) (18) (19) 为探讨(12)式中风险中性概率的分布形状,下面在不同的参数设置下对g(ST|St)进行模拟分析。 (1)假定当期现货价格St=2.500,未来到期日的现货价格ST以0.025的步长从1.500~3.500变化,期权存续期为半年(约180天),年无风险利率为0.500。 (2)通过β2的不同取值分析时变波动率对于风险中性概率分布的影响。图1给出当收益率为正态分布时,β1固定为-2时,风险中性概率分布形状受β2变化的影响。由图1可知,在β1固定的条件下,当β2= 0时所得分布恰为经典B-S模型下的风险中性概率分布,β2取值越大得到的风险中性概率分布越正偏。 (3)比较LYE et al.[38]提出的广义学生t分布(7)式在参数赋值约束条件下所得的风险中性概率分布g-gst[ST]与经典B-S模型中的风险中性概率分布g-logn[ST]的一致性,图2给出在同一坐标轴下g-gst[ST]和g-logn[ST]的风险中性概率分布。由图2可知,两种情况下的风险中性概率密度分布完全重合,很好地证实了广义学生t分布可以通过参数赋值得到经典B-S模型中的风险中性概率分布,进而为本研究的Normal模型和Mixture模型的构建提供了有力的支撑。 本研究样本数据为2015年2月9日、2015年2月16日和2015年2月25日的每日欧式看涨期权的一分钟高频报价以及同一时刻的现货价格,数据来源于Wind资讯。由于沪深股票交易所在每个交易日的9:30分开盘,到11:30中午休市,然后在13:00开盘,到15:00收盘,每天有4个小时共240分钟的连续竞价交易时间,对于每一交易日的20份欧式看涨期权,可获得4 800个样本点。另外,分别选取与上述3日相邻交易日的高频数据用于对本研究构建模型的预测效果评估。以2015年2月9日为例,首先估计得到该交易日对应期权定价模型的参数,然后运用这些参数分别对2015年2月10日和2015年2月11日的期权价格进行预测,最后比较预测价格与实际价格之间的误差。 图1 收益率为正态分布条件下β2变化对于风险中性概率分布的影响Figure 1 The Influence of the Variation of the β2on Risk Neutral Probability Distributions, Assuming Normality in Returns 图2 广义学生t分布与经典B-S模型的风险中性概率分布Figure 2 Risk Neutral Probability Distributions for GST and B-S (a)收益率波动 (b)收益率频率 均值标准差偏度峰度J⁃BADFQ(8)Q(9)2015年2月9日0.0080.1240.611∗∗∗2.356∗∗∗1408.900∗∗∗-15.146∗∗∗88.113∗∗∗89.780∗∗∗ 注:***为在1%水平下显著,下同;峰度为超额峰度系数,正态分布的超额峰度系数为0.000;J-B为检验收益率是否服从正态分布的Jarque-Bera统计量;ADF为以最小AIC准则确定最优检验滞后阶数后得到的Augmented Dickey-Fuller单位根检验统计量;Q(8)为滞后阶数为8的收益率Ljung-BoxQ统计量;Q(9)为滞后阶数为9的收益率Ljung-BoxQ统计量。 需要指出的是,若本研究所构建的Normal模型与Mixture模型涉及分红时,需要对模型中的现货价格St进行Ste-diτ分红剔除处理,其中di为分红比例;然后用剔除分红后的现货价格Ste-diτ替换现货价格St并代入模型,即可求得考虑分红因素后的理论期权价格。然而本研究的实证研究对象50ETF在2015年度并无分红记录,即使根据最近4次的历史分红记录算出平均分红比例di=0.410%(数据来源于wind资讯),在各存续期下e-diτ≈1,由此可知中国标的50ETF的分红对于期权定价的研究结论并无显著影响。 另外,若令Pt为每分钟报价,T为样本总数,则高频收益率rt(t=1, 2, …,T)可以表示为 rt=100×[ln(Pt)-ln(Pt-1)] (20) 图3、表1和表2分别给出2015年2月9日当天的标的资产收益率波动与分布、标的收益率的描述性统计结果和期权价格,2015年2月16日和2015年2月25日的数据也具有类似统计特征,限于篇幅,不再给出。 由图3、表1和表2可知: (1)图3(a)中标的资产收益率波动随时间的变化而变化,说明中国50ETF期权的标的资产收益率具有较为明显的时变波动性特征。 (2)50ETF期权的标的资产收益率不服从正态分布。由图3(b)可以发现该分布具有尖峰厚尾和有偏等特征,表1中偏度、峰度以及J-B统计量等均在1%水平下显著,也说明标的资产收益率的非正态性。 表2 50ETF期权价格数据Table 2 50ETF Options Price Data (3)表1中的ADF单位根检验结果表明,50ETF期权合约的标的资产收益率序列存在单位根的零假设被强烈拒绝,可以认为中国50ETF期权的标的资产收益率序列是平稳的,进而可以直接作为下一步极大似然的计量建模。 (4)从表1基于滞后8阶和9阶的Ljung-BoxQ统计量可以看出,在相对较高的显著性水平上(1%),都可以拒绝50ETF期权的标的资产收益率在较长的时间范围内(滞后8期或9期)都不具有自相关性的原假设,即50ETF标的资产的价格中存在较为明显的长记忆性。 本研究采用的无风险利率为中国人民银行2015年2月份公布的1年期定期存款利率,即r=2.750%。 上文对中国50ETF期权及其标的资产收益率的时变波动性特征和非正态性的分析为运用本研究构建的模型提供了经验证据,下面用本研究构建的Normal模型((13)式)和Mixture模型((18)式)分别计算对应模型下的t时刻第j份期权的理论价格,具体表示为 F(St)j=F(St,Xj,τj,r;Ω) (21) 其中,F(St)j为第j份期权在t时刻的理论价格,Xj为第j份期权的执行价格,τj为第j份期权的存续期,Ω为描述标的资产收益率分布和波动的参数向量。当Ω={β1}时,即为本研究所构建的经典B-S期权定价模型(即(16)式)。另外,t时刻第j份期权市场价格Cj,t与理论价格F(St)j之间的相关关系为 Cj,t=F(St)j+εj,t (22) (23) 其中,Φ1和Φ2均为未知参数。设N为样本观测个数,则对数似然函数的表达式为 (24) 其中,L为似然函数值。 对于上文所涉及的Φ1、Φ2和Ω,均采用GAUSS 9.0程序MAXLIK软件包进行极大似然估计。本研究中(5)式的ST、(8)式的zT均通过取倒数变换,将对应积分函数的上下限转换为(-1,1),然后采用INTQUAD1命令进行一维数值积分,求得期权的理论价格。 表3和表4分别给出Normal模型和Mixture模型在3个交易日下经极大似然估计得出的参数值、标准差以及显著性水平。 表3 Normal模型在不同交易日的极大似然估计Table 3 Maximum Likelihood Estimates of the Normal Model for Various Trading Days 表4 Mixture模型在不同交易日的极大似然估计Table 4 Maximum Likelihood Estimates of the Mixture Model for Various Trading Days 由表3和表4可知: (2)在Mixture模型下3个交易日的参数α均显著,证明中国50ETF期权的标的资产收益率分布存在非正态性,因此采用MELICK et al.[39]提出的混合对数正态分布对真实分布进行刻画,构建本研究提出的Mixture模型能够显著提高期权的定价精度。 (3)根据表3和表4的结果,除在Normal模型下的交易日2015年2月25日外,其余交易日下的参数Φ2均显著,证明定价误差的方差与期权实值程度之间确实存在显著相关关系。 为了对Normal模型和Mixture模型进行定价精确性分析,本研究运用这两种模型分别计算其对应的理论价格F(St)j与各自的市场价格Cj,t在平均绝对误差(MAE)、平均误差平方(MSE)、经异方差调整的MAE(HMAE)、经异方差调整的MSE(HMSE)、对数损失函数误差(R2LOG)以及高斯准极大似然函数误差(QLIKE)等6种常用的损失函数下进行比较,6种损失函数的具体表达式为 (25) (26) (27) (28) (29) (30) 表5 模型定价偏差Table 5 Mispricing of the Models 考虑到Normal模型与Mixture模型进行极大似然估计时具有不同的参数维数κ和似然函数值L的性质,因而在比较Normal模型与Mixture模型定价偏差时也分别计算了AIC和SIC统计量,表5分别给出在3个交易日下Normal模型和Mixture模型关于定价偏差的具体损失函数值和统计量。当模型的损失函数值(MAE、MSE、HMAE、HMSE、R2LOG、QLIKE)和统计量(AIC、SIC)相对较小时即表示对应模型在该定价偏差衡量指标中表现较优,进而表示相应的期权定价模型具有更高的定价精度。另外,如果当Normal模型和Mixture模型在同一交易日下某些定价偏差衡量指标表现一致时,本研究以在该交易日下的其他定价偏差衡量指标为准。 由表5可知,2015年2月9日Normal模型与Mixture模型在MAE、MSE和QLIKE定价偏差衡量标准下数值相等,即模型定价偏差效果表现一致,而在HMAE、HMSE、R2LOG、AIC和SIC定价偏差衡量标准下,Mixture模型比Normal模型数值较小,即Mixture模型比Normal模型对期权的定价精度更高。同理,对于2015年2月16日和25日也可以发现在对中国50ETF期权定价精度上,Mixture模型明显优于Normal模型。 为进一步对Mixture模型和Normal模型进行比较,本研究分别采用对2015年2月9日、2015年2月16日和2015年2月25日估计出的参数对相邻交易日期权价格进行预测,并对其预测精确性进行比较。以2015年2月9日为例,首先采用极大似然估计方法得到该日的参数,然后分别用该日估计的参数计算2015年2月10日和11日的期权价格,最后计算对应模型的预测误差,即 fj,t=Cj,t-F(St)j|Feb,9th (31) 其中,fj,t为第j份期权在t交易日的价格预测误差,Cj,t为第j份期权在t交易日的期权市场价格,t分别为2015年2月10日和11日,且 F(St)j|Feb,9th=F(St,Xj,τj,r;ΩFeb,9th) (32) 其中,ΩFeb,9th为用2015年2月9日数据估计得到的参数。然后可通过(31)式求得相应的预测误差。同理可以用2015年2月16日估计的参数预测2015年2月17日(2015年2月18日为春节假日)的期权价格,用2015年2月25日估计的参数预测2015年2月26日和27日的期权价格。 为提高稳健性,本研究分别采用MAE、MSE、HMAE、HMSE、R2LOG、QLIKE损失函数和DM统计量对模型预测精度进行评估。在对模型预测效果的衡量标准中,由于预测误差数值偏小,因而采用均方根误差(RMSE)替代平均平方误差(MSE)作为模型预测效果评判标准,以便于直观地比较。本研究采用的RMSE损失函数的具体表达式为 (33) 本研究采用DM统计量检验Mixture模型与Normal模型的预测误差之间差异是否显著,其原假设为两模型之间具有一致的预测精确性,且该统计量渐近服从N(0,1)分布,表达式为 (34) 其中,diffj,t为第j份合约在t时刻Mixture模型与Normal模型预测误差之间的差异。 表6分别给出Normal模型和Mixture模型关于期权价格预测效果的损失函数值和统计量。若在某一交易日下对应模型的损失函数值越小,表示该模型对于期权价格的预测精确性更高。另外,当DM统计量的绝对值均大于1.960时,表示在5%水平下拒绝原假设,即Normal模型与Mixture模型的预测误差之间具有显著性差异。由表6可知在各个交易日下的DM的绝对值都大于1.960,且统计量均在5%的水平下显著,说明Normal模型与Mixture模型在对中国50ETF期权价格预测上具有显著性的差异。 表6 模型预测效果Table 6 Forecasting Performance of the Models 注:**为在5%水平下显著,黑体数据为在某一预测效果衡量标准下Nomral模型与Mixture模型中的较小值,如果在同一交易日下某一预测效果衡量标准数值相等,则表示Nomral模型与Mixture模型在该预测效果衡量标准下表现一致。 由表6可知,2015年2月10日Normal模型与Mixture模型在MAE、RMSE、HMSE和QLIKE预测效果衡量标准下数值相等,即模型的预测效果表现一致;而在HMAE、R2LOG预测效果衡量标准下Mixture模型比Normal模型数值较小,即Mixture模型比Normal模型对期权的预测效果更好。同理,2015年2月11日和17日Normal模型与Mixture模型在MAE和RMSE预测效果衡量标准下表现一致,而在HMAE、HMSE、R2LOG和QLIKE预测效果衡量标准下Mixture模型优于Normal模型;2015年2月26日和27日Normal模型与Mixture模型在MAE、RMSE、HMSE、R2LOG和QLIKE预测效果衡量标准下表现一致,仅在HMAE预测效果衡量下Normal模型优于Mixture模型。通过整体计数在5个交易日下Normal模型与Mixture模型出现较优预测表现的次数(即黑体数据的个数)可以发现,Mixture模型在对期权价格的预测表现上整体优于Normal模型。 本研究采用ROSENBERG et al.[36-37]的条件波动率进行时变波动率修正,运用LYE et al.[38]的灵活参数分布重构具有时变波动性特征的B-S模型并演示了其风险中性概率分布形状,引入MELICK et al.[39]的混合对数正态分布捕捉标的资产收益率非正态分布特征,通过对中国50ETF期权实证比较了Mixture模型和Normal模型的参数显著性、定价偏差和预测效果,得到以下研究结论。 ①通过对中国50ETF期权的标的资产价格变化的动力学特征深入考察,发现其高频收益呈现较为明显有偏和尖峰厚尾分布;②从Normal模型和Mixture模型的极大似然参数估计结果也可以发现,刻画中国50ETF期权标的资产时变波动性特征的参数β2、β1,2和β2,2显著,充分说明中国50ETF期权标的资产具有显著的时变波动性特征,进而证实基于经典B-S模型理论基础进行SSP形式时变波动率修正后的期权定价模型能够显著改善期权的定价精度;③在中国推出真正意义的期权产品的背景下,本研究提出的具有时变波动性特征的B-S模型和具有时变波动性特征的混合对数正态模型都能深入和全面地描绘标的资产收益的波动和分布;④综合考虑模型对标的资产价格变化动力学的刻画效果以及对中国50ETF期权在样本内的定价偏差和在样本外的预测误差后,发现具有时变波动性特征的混合对数正态模型比具有时变波动性特征的B-S模型具有更高的定价精确性,即基于时变波动率与混合对数正态分布修正后的B-S模型是一个相对更优的期权定价模型选择。 本研究结果为期权定价提供了更好的方法选择,也丰富了期权定价的实证结果,进而为投资者设计更为合理的投资策略以及为金融监管当局提供更加准确的决策信息支持意义重大。当然,本研究还存在一些不足,对于标的资产收益率的其他分布、模型的Delta对冲、波动率偏离的修正需要进一步研究,这也是下一步研究的重点。 [1]BLACK F,SCHOLES M.The pricing of options and corporate liabilities.JournalofPoliticalEconomy,1973,81(3):637-654. [2]龙海明,李占国,蒋鑫,等.产业链金融视角下财务公司融资产品定价研究:基于模糊B-S欧式看跌期权模型.财经理论与实践,2015,36(2):2-8. LONG Haiming,LI Zhanguo,JIANG Xin,et al.The research on financing product pricing of financial company from the perspective of the industrial chain finance:based on the fuzzy B-S European put option pricing model.TheTheoryandPracticeofFinanceandEconomics,2015,36(2):2-8.(in Chinese) [3]鲍继业,张恒.博弈框架下巴黎期权性质的可转换债券定价.管理科学,2013,26(1):80-88. BAO Jiye,ZHANG Heng.A game approach to the pricing of convertible bonds with Parisian options characteristics.JournalofManagementScience,2013,26(1):80-88.(in Chinese) [4]张卫国,史庆盛,许文坤.基于全最小二乘拟蒙特卡罗方法的可转债定价研究.管理科学,2011,24(1):82-89. ZHANG Weiguo,SHI Qingsheng,XU Wenkun.Pricing model of convertible bonds in China by total least-squares quasi-Monte Carlo method.JournalofManagementScience,2011,24(1):82-89.(in Chinese) [5]GUIDOLIN M,HANSEN E.Pricing S&P 500 index options:a conditional semi-nonparametric approach.JournalofFuturesMarkets,2016,36(3):217-239. [6]CORDIS A S,KIRBY C.Discrete stochastic autoregressive volatility.JournalofBanking&Finance,2014,43:160-178. [7]PARK B J.Time-varying,heterogeneous risk aversion and dynamics of asset prices among boundedly rational agents.JournalofBanking&Finance,2014,43:150-159. [8]HUSSAIN S I,LI S.Modeling the distribution of extreme returns in the Chinese stock market.JournalofInternationalFinancialMarkets,Institutions&Money,2015,34:263-276. [9]WU C C,LIN Z Y.An economic evaluation of stock-bond return comovements with copula-based GARCH models.QuantitativeFinance,2014,14(7):1283-1296. [10] 刘攀,周若媚.AEPD、AST和ALD分布下金融资产收益率典型事实描述与VaR度量.中国管理科学,2015,23(2):21-28. LIU Pan,ZHOU Ruomei.Description of the typical characteristics of financial asset′s yield distribution and VaR models based on AEPD、AST and ALD distribution.ChineseJournalofManagementScience,2015,23(2):21-28.(in Chinese) [11] 孙艳,何建敏,周伟.基于UHF-EGARCH模型的股指期货市场实证研究.管理科学,2011,24(6):113-120. SUN Yan,HE Jianmin,ZHOU Wei.Empirical research on the stock index market based on the UHF-EGARCH model.JournalofManagementScience,2011,24(6):113-120.(in Chinese) [12] 苏云鹏,杨宝臣.随机波动HJM框架下可违约债券市场波动结构的实证研究.管理科学,2015,28(1):122-132. SU Yunpeng,YANG Baochen.Empirical research on volatility structure of defaultable bond market under HJM framework with stochastic volatility.JournalofManagementScience,2015,28(1):122-132.(in Chinese) [13] CHRISTOFFERSEN P,HESTON S,JACOBS K.Capturing option anomalies with a variance-dependent pricing kernel.ReviewofFinancialStudies,2013,26(8):1962-2006. [14] BYUN S J,JEON B H,MIN B,et al.The role of the variance premium in Jump-GARCH option pricing.JournalofBanking&Finance,2015,59:38-56. [15] CHRISTOFFERSEN P,FEUNOU B,JACOBS K,et al.The economic value of realized volatility:using high-frequency returns for option valuation.JournalofFinancialandQuantitativeAnalysis,2014,49(3):663-697. [16] CORSI F,FUSARI N,LA VECCHIA D.Realizing smiles:options pricing with realized volatility.JournalofFinancialEconomics,2013,107(2):284-304. [17] CHEN S X,XU Z.On implied volatility for options:some reasons to smile and more to correct.JournalofEconometrics,2014,179(1):1-15. [19] 柳向东,杨飞,彭智.随机波动率模型下的VIX期权定价.应用数学学报,2015,38(2):285-292. LIU Xiangdong,YANG Fei,PENG Zhi.The VIX option pricing based on stochastic volatility models.ActaMathematicaeApplicataeSinica,2015,38(2):285-292.(in Chinese) [20] 徐蕾,邓国和.随机波动率模型下欧式回望期权定价.广西师范大学学报:自然科学版,2015,33(3):79-90. XU Lei,DENG Guohe.Valuation on European lookback option under stochastic volatility model.JournalofGuangxiNormalUniversity:NaturalScienceEdition,2015,33(3):79-90.(in Chinese) [21] 邓国和.随机波动率跳跃扩散模型下复合期权定价.数理统计与管理,2015,34(5):910-922. DENG Guohe.Pricing compound option in a stochastic volatility jump-diffusion model.JournalofAppliedStatisticsandManagement,2015,34(5):910-922.(in Chinese) [22] 赵攀,肖庆宪.基于Tsallis分布及跳扩散过程的欧式期权定价.中国管理科学,2015,23(6):41-48. ZHAO Pan,XIAO Qingxian.Pricing of European options based on Tsallis distribution and jump-diffusion process.ChineseJournalofManagementScience,2015,23(6):41-48.(in Chinese) [23] KIM J,KIM H.Option implied tail index and volatility based on heavy-tailed distributions:evidence from KOSPI 200 Index options market.GlobalEconomicReview,2014,43(3):269-284. [24] HUANG C S,HUANG C K,CHINHAMU K.Assessing the relative performance of heavy-tailed distributions:empirical evidence from the Johannesburg stock exchange.JournalofAppliedBusinessResearch,2014,30(4):1263-1286. [25] JIMÉNEZ J A,ARUNACHALAM V,SERNA G M.Option pricing based on the generalised Tukey distribution.InternationalJournalofFinancialMarketsandDerivatives,2014,3(3):191-221. [26] MOSCOSO J A J,ARUNACHALAM V,SERNA G M.A generalization of Tukey′s G-H family of distributions.JournalofStatisticalTheoryandApplications,2015,14(1):28-44. [27] FRY-MCKIBBIN R,MARTIN V L,TANG C.Financial contagion and asset pricing.JournalofBanking&Finance,2014,47:296-308. [28] RECCHIONI M C,SUN Y.Cannegativeinterestratesreallyaffectoptionpricing?Empiricalevidencefromanexplicitlysolvablestochasticvolatilitymodel.Ancona:Università Politecnica Delle Marche,2016. [29] LEIPPOLD M, SCHARER S.Discrete-timeoptionpricingwithstochasticvolatility.Zurich:University of Zurich,2016. [30] CHRISTOFFERSEN P,JACOBS K,ORNTHANALAI C.Dynamic jump intensities and risk premiums:evidence from S&P500 returns and options.JournalofFinancialEconomics,2012,106(3):447-472. [31] 吴鑫育,杨文昱,马超群,等.基于非仿射随机波动率模型的期权定价研究.中国管理科学,2013,21(1):1-7. WU Xinyu,YANG Wenyu,MA Chaoqun,et al.Option pricing under non-affine stochastic volatility model.ChineseJournalofManagementScience,2013,21(1):1-7.(in Chinese) [32] 郑宁,殷俊锋,徐承龙.投影三角分解法定价带随机波动率的美式期权.应用数学与计算数学学报,2013,27(1):114-127. ZHENG Ning,YIN Junfeng,XU Chenglong.Projected triangular decomposition method for pricing American option under stochastic volatility model.CommunicationonAppliedMathematicsandComputation,2013,27(1):114-127.(in Chinese) [33] THEODOSSIOU P.Skewed generalized error distribution of financial assets and option pricing.MultinaitonalFinanceJournal,2015,19(4):223-266. [34] CASSIDY D T,HAMP M J,OUYED R.Log student′st-distribution based option sensitivities:Greeks for the Gosset formulae.QuantitativeFinance,2013,13(8):1289-1302. [35] 杨瑞杰.期权交易能提高标的资产的定价效率吗?基于上证50ETF套利视角的实证研究.金融发展研究,2015(10):43-46. YANG Ruijie.Can options trading improve the pricing efficiency of underlying assets?An empirical study from the perspective of SSE 50ETF arbitrage.JournalofFinancialDevelopmentResearch,2015(10):43-46.(in Chinese) [36] ROSENBERG J V,ENGLE R F.Optionhedgingusingempiricalpricingkernels.NBER Working Paper,1997. [37] ROSENBERG J V.Pricing multivariate contingent claims using estimated risk-neutral density functions.JournalofInternationalMoneyandFinance,1998,17(2):229-247. [38] LYE J N,MARTIN V L.Non-linear time series modelling and distributional flexibility.JournalofTimeSeriesAnalysis,1994,15(1):65-84. [39] MELICK W R,THOMAS C P.Recovering an asset′s implied PDF from option prices:an application to crude oil during the gulf crisis.JournalofFinancialandQuantitativeAnalysis,1997,32(1):91-115. [40] LIM G C,MARTIN G M,MARTIN V L.Parametric pricing of higher order moments in S&P500 options.JournalofAppliedEconometrics,2005,20(3):377-404. [41] INGERSOLL J E,Jr.Theory of financial decision making∥RowmanandLittlefieldStudiesinFinancialEconomics,1987:691-693. [42] HULL J C.Options,futures,andotherderivativesecurities.4th ed,Prentice Hall:New Jersey,2000:259-263. [43] ENGLE R F,MUSTAFA C.Implied ARCH models from options prices.JournalofEconometrics,1992,52(1/2):289-311. OptionPricingofMixtureofLognormalDistributionswithTime-varyingVolatilityin50ETFOption WANG Peng,YANG Xinglin Institute of Chinese Financial Studies, Southwestern University of Finance and Economics, Chengdu 611130, China The classic Black-Scholes model has experienced the development process from the constant volatility to time-varying volatility and from the normal distribution to non-normal distribution. This paper extends prior studies on option pricing models with time-varying volatility and mixture of lognormal distributions. Two frameworks have been proposed to correct misspecification of Black-Scholes model. The first category involves relaxing the constant volatility assumption with sigma shape polynomial (SSP), in which the specification shows that conditional volatility is stochastic, as it is a function of future return over the life of the option. The second category involves relaxing the normality assumption using mixture of lognormal distributions, which can capture departures from normal returns with two subordinate lognormal distributions. Furthermore, we rebuild the Black-Scholes model based on the generalized Student t-distribution and study the risk neutral probability distribution, which is changed along with the alternative volatility parameterizations, assuming normality in stock returns. The empirical application is based on 50ETF call options′ contracts traded on the selected days in the month of February 2015, a total sample of over 10000 observations. Each record in the data set comprises bid-ask quote, the synchronously recorded spot price of 50ETF, the time at which the quote was recorded, and the strike price. In addition, a range of performance criteria are used to evaluate the model. The first consists of conducting standard tests of significance on the parameter estimates. The second concentrates on comparing the relative size of mispricing errors of each model. The third focuses on comparing the relative size of forecasting errors of each model. Finally, the empirical results show that there are some significant characteristics of leverage effect, clustering, and long memory as well as conditional skewness and fat-tail in the high frequency yield of underlying assets of the 50ETF option contracts. Meanwhile, the modified classic Black-Scholes model with time-varying volatility can significantly improve the pricing accuracy of 50ETF option contracts in China. Furthermore, in considering the model of the underlying asset price changes in the dynamics of depict and the pricing accuracy on the option contract, the option pricing model with the characteristics of time-varying volatility and mixture of lognormal distributions is a relatively more reasonable option pricing model selection, compared with that of correcting the volatility skew associated with the Black-Scholes model. This paper not only provides a more accurate option pricing method for investors and regulators, but also enriches the empirical research conclusions about the typical statistical characteristics of 50ETF option contracts in China. mixture of lognormal distribution;time-varying volatility;Black-Scholes model;option pricing;50ETF Date:February 29th, 2016 DateJune 3rd, 2016 FundedProject:Supported by the National Natural Science Foundation of China(71473200) and the Humanities and Social Science Research Project of China(15YJA790057) Biography:WANG Peng, doctor in management, is an associate professor in the Institute of Chinese Financial Studies at Southwestern University of Finance and Economics. His research interests include financial risk management and financial econometrics. His representative paper titled “Dilemma of classical financial theory and the rising of econophysics” was published in theJournalofManagementSciencesinChina(Issue 9, 2014). E-mail:wangpengcd@126.com YANG Xinglin is a master degree candidate in the Institute of Chinese Financial Studies at Southwestern University of Finance and Economics. His research interest focuses on derivative pricing. E-mail:xinglinyang@2015.swufe.edu.cn F830.9 A 10.3969/j.issn.1672-0334.2016.04.013 1672-0334(2016)04-0149-12 2016-02-29修返日期2016-06-03 国家自然科学基金(71473200);教育部人文社会科学研究规划基金(15YJA790057) 王鹏,管理学博士,西南财经大学中国金融研究中心副教授,研究方向为金融风险管理和金融计量经济学等,代表性学术成果为“经典金融理论的困境与金融物理学研究的兴起”,发表在2014年第9期《管理科学学报》,E-mail:wangpengcd@126.com 杨兴林,西南财经大学中国金融研究中心硕士研究生,研究方向为衍生品定价等,E-mail:xinglinyang@2015.swufe.edu.cn □


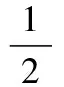
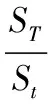
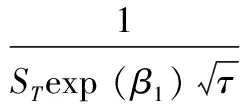
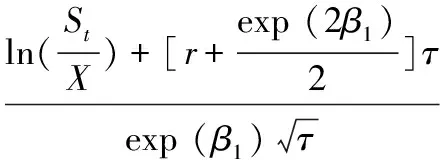
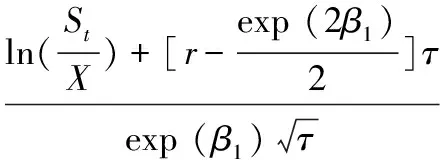
3.3 构建具有时变波动性特征的混合对数正态模型
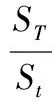
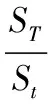
4 具有时变波动性特征的风险中性概率分布模拟
5 Normal模型与Mixture模型实证研究结果对比
5.1 数据描述

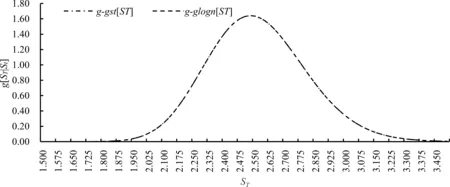
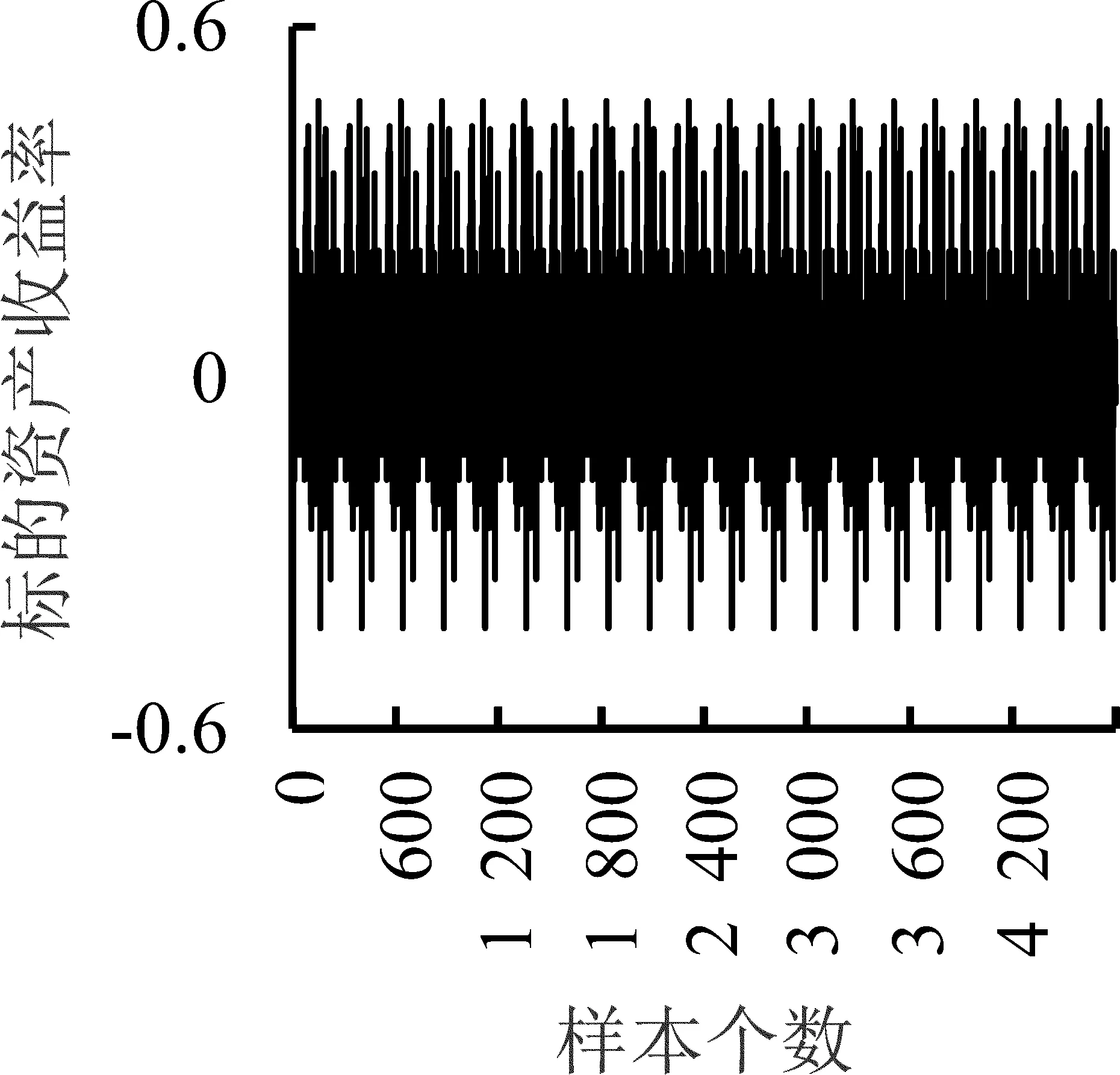
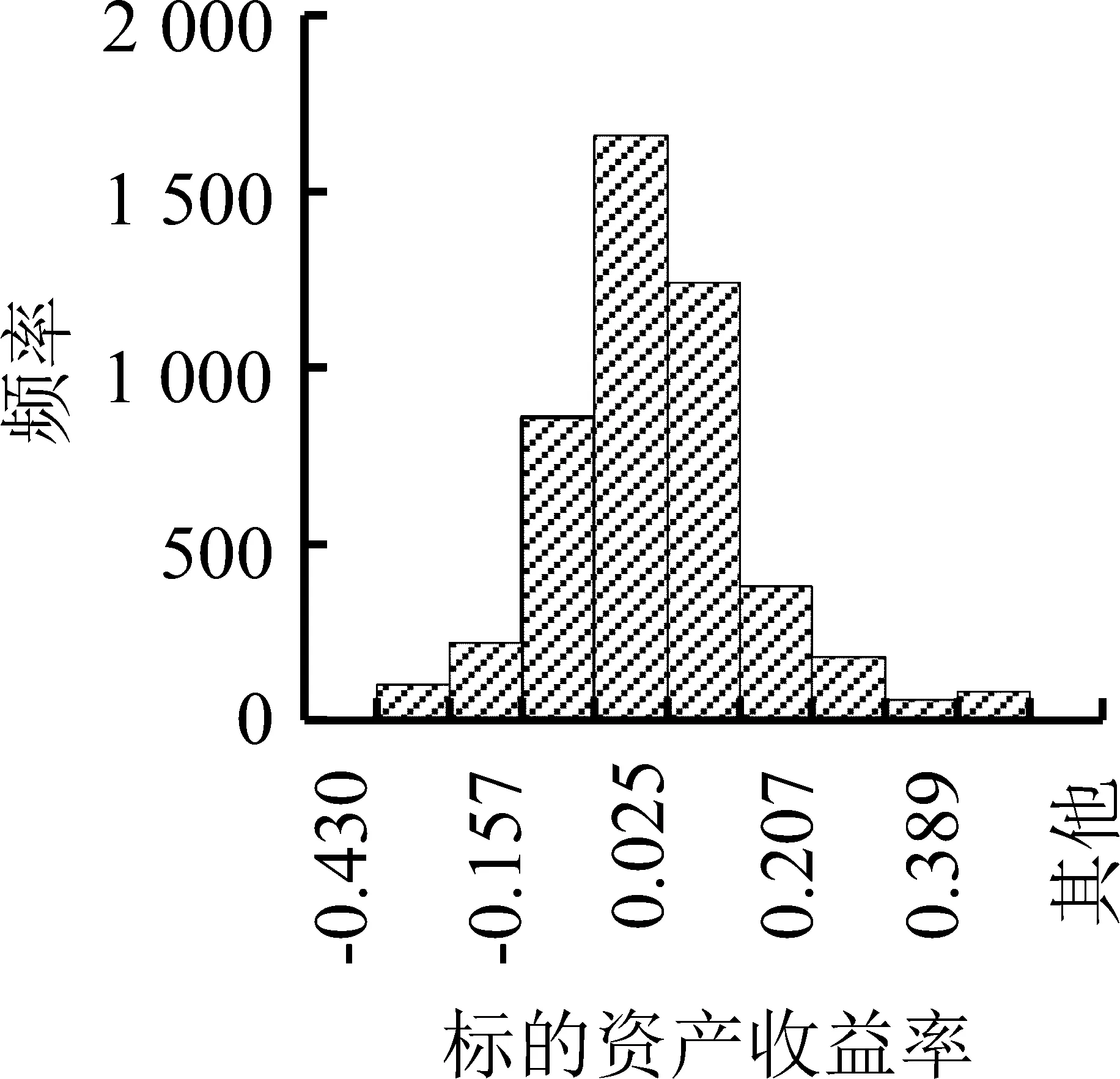

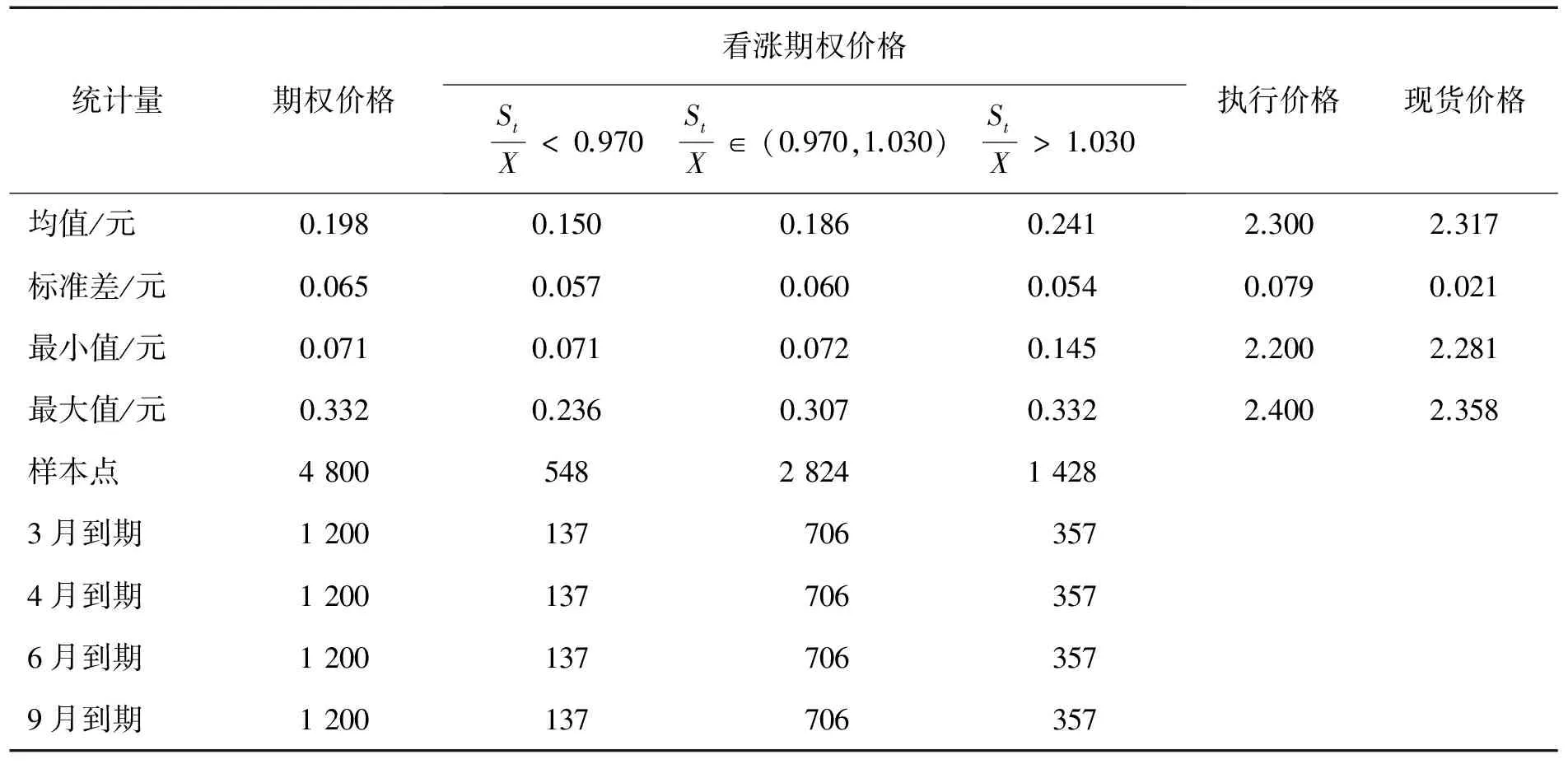
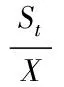
5.2 参数估计

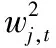
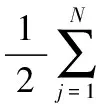
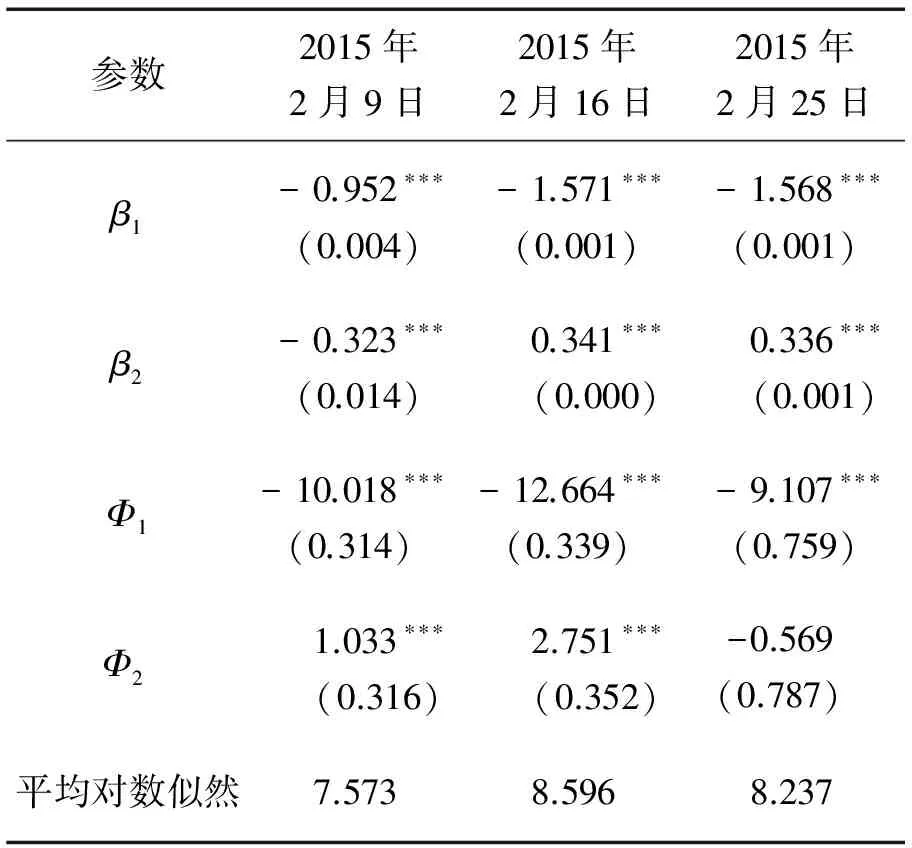
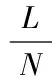

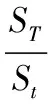
5.3 Normal模型与Mixture模型定价偏差比较
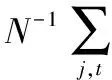
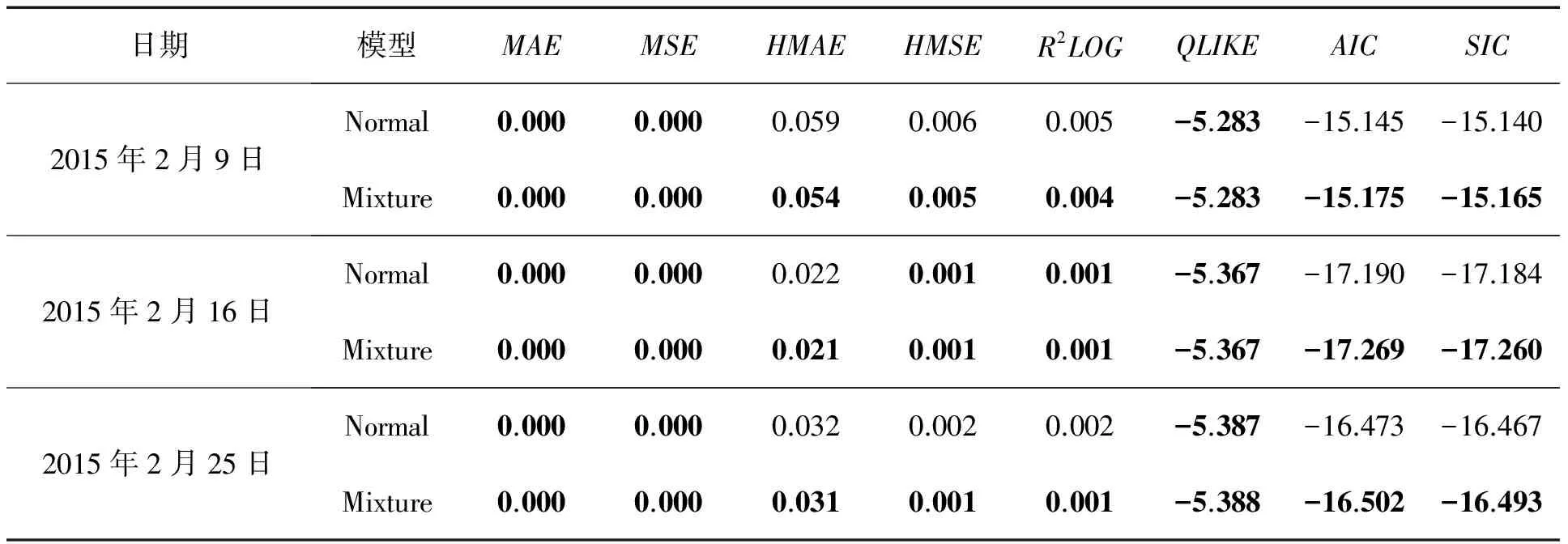
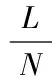
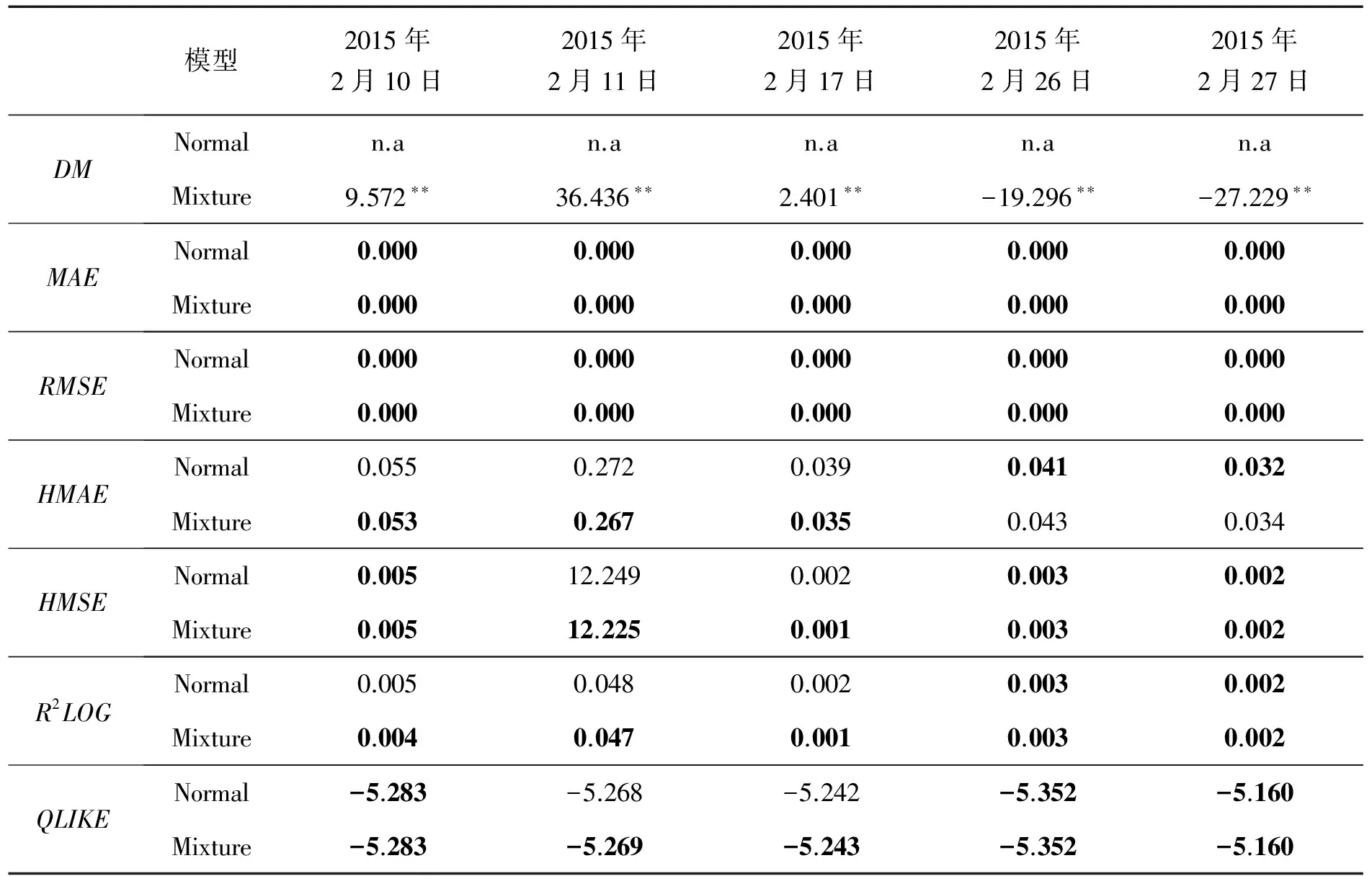
5.4 Normal模型与Mixture模型预测比较
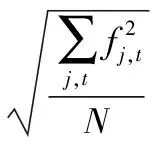
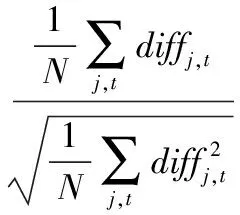
6 结论

