科学用教材引导“再创造”

颜乙红

在弗赖登塔尔看来，学习数学的正确方法是实行“再创造”。将数学作为一种活动来进行解释和分析，建立在这一基础上的教学方法，称之为再创造方法。为此，在教学时，教师不必将各种规则、定律灌输给学生，而应该创造合适的条件，提供很多具体的例子，引导和帮助学生去进行再创造的工作。这是一种最自然最有效的学习方法。教材是师生进行教与学的主要依据，是“再创造”学习的重要载体，如何科学使用教材引导学生“经历数学学习的“再创造”，笔者试图从以下方面提出几点看法。

一、丰富情境资源，明晰“再创造”的活动线索

创造性的学习是有线索的，那就是学生的知识经验和活动经验。但线索有时受到教材和教师教学的局限，显得单一甚至唯一。为此必须领会教材意图，在原有情境资源的基础上“添砖加瓦”，促成数学学习更加丰富、厚实。

例如：北师大版三年下册《认识分数》中的分一分（一）。

学生在认识了整数和小数后，第一次接触分数。教材创设了淘气和笑笑分苹果的生活情境图。图（1）2个苹果，平均分后每人得到1个苹果，每份数是整数。图（2）1个苹果平均分后每人分到这个苹果的一半，每份数不是整数。由此让学生体会到“创造”一种新的数（分数）来表示一半的必要性。情境图旨在引导学生经历分数产生和发展的过程，加深对分数意义的理解。两幅图为学生的“再创造”创设一个支点，“再创造”的同学，每人分到2个苹果。师：这样呢？

生：2个苹果，平均分给2个同学，每人分到1个。

师：1个苹果平均分给2个同学，每人又分到多少？线索是平均分，是除法，但教材情境比较单薄，我是这样处理的：

师：8个苹果，平均分给2个同学，每人分到几个？你是怎么想的？

生：每人分到4个，因为8除以2等于4。

（课件展示竖线平均分成2份的过程）

师：那这幅又可以表示什么？

生：4个苹果平均分给2个

生：半个？

师：你能用什么方式表示一半？

这样从每人分到4个再到2个、1个，再到思考能用什么方式表示一半？从不同的角度唤醒学生平均分的知识、活动经验。设计既遵循教材的编排意图，又不囿于教材。虽然这节课的重点不在于让学生了解分数与除法的联系，但正如弗莱登塔尔所说的：“建造一幢大楼，应该从图纸开始，在打基础以前应该先知道究竟要将大楼建造得多高。”追根溯源,让学生意识到除法产生分数，从而使表示一半的“再创造”学习活动线索更清晰。

二、细化问题资源，领会“再创造”的活动目的

数学天生就是与问题联系在一起，从特定情境出发，展开一组问题，学生可以在教师引导下理解情境、解决问题，经历数学学习的“再创造”。“情境+问题串”的呈现为自然而然地展开学生的数学学习过程和教师的教学过程提供基础环境和主要脉络，但有时教材呈现的问题表现为引导学生解决问题的步骤，而没有体现启发学生思考活动的目的，导致课堂表面很热闹，学生实质很懵懂。此时，可以细化问题资源，提出启发性的问题填补学生理解上的缝隙，领会活动目的。

例如：北师版教材在三年下册《两位数乘两位数》单元的第一课时队列表演（一）

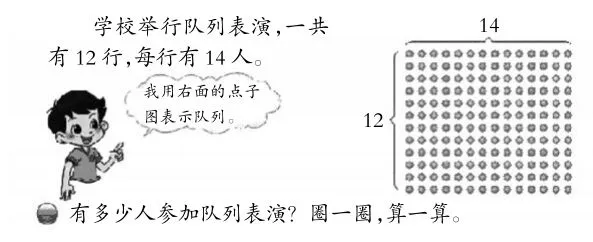
教材呈现队列表演的情境，增加点子图，意图通过点子图这个直观载体，帮助学生更好地理解、掌握两位数乘两位数的算理模型及算法。数形结合，为学生的“再创造”学习提供强有力的背景支持。然而在教学中，在点子图和“有多少人参加队列表演？圈一圈，算一算”这问题之间，缺乏一个承上启下的问题过渡，学生“再创造”的目的不明确，想和做之间出现裂缝，我是这样处理的：

1.出示教材队列表演的情境。提出问题：有多少人参加表演？

2.利用课件把每行每列的人数转化成小圆点，得出：有多少人参加队列表演，就有多少个点。出示14×12的点子图。

3.提出问题：你会怎样算这个点子图共有多少个点？把你的想法在图上圈一圈，然后把计算过程写下来。

这样在立足教材的前提下，只添了一个启发性衔接问题“你会怎样算这个点子图共有多少个点？”使学生接下来的“再创造”学习活动目的明确又极具启发性：

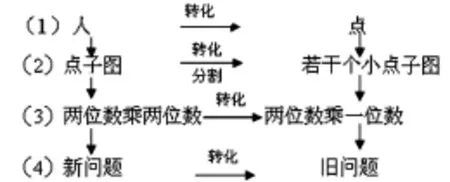
目的明确，活动才能成为思维的脚手架，数学思想的渗透也就水到渠成了。

三、活用插图资源，拓宽“再创造”的思维宽度

教材提供了很多有趣的、现实的、蕴含数学意义和富有挑战性的插图，帮助学生理解、掌握知识。活用这些插图资源，对它们进行适当的改造、重组，可以拓宽“再创造”的思维宽度。例如，北师大版三年下册《面积单位》一课，提供这么一组插图。目的是引导学生感知、体验面积单位的实际大小。根据教材提供的“用报纸拼一个1平方米的正方形”这一插图，在引导学生感受1平方米时，我是这样处理的：

1.建构。

师：1平方米有多大？

生：边长是1米的正方形那么大。

师：是这么大吗？（事先把1平方米的报纸对折再对折成原正方形的）

生1：不是，太小了，要再长一点。

生2：用米尺量出1米。

生：不是，每条边都要一样长，每条边都要1米。

师：是这样吗？（全部展开）

生：（惊讶，激动）哇，1平方米这么大。

2.体验。

师：如果站在这1平方米的报纸上，大约可站多少人？试一试。

（当场体验）

生：大约12人。

师：24个鞋印大约是1平方米。

3.变式。

师：如果老师把这报纸剪开（把报纸对折剪），拼成一个这样的长方形，这个长方形的面积有多大？

生：还是1平方米。

师：为什么？

生：形状变了，面积没变。

师：刚才的正方形还可能变成______？

生：三角形、平行四边形。

师：如果随便撕成2部分，这两部分的面积有多大？为什么?

生：还是1平方米。面积没有增加也没有减少。

师：不管图形怎样变化，面积还是1平方米。

在上述的教学片断中，我抓住教材提供的插图资源，使用的仅仅是一张课前拼接的报纸，分层建构了1平方米的表象，使学生对概念的理解达到更高的认知水平——边长1米的正方形，面积是1平方米，但1平方米不一定就是边长1米的正方形，它可以是同样大小的任何形状的物体。立足教材，由一个点生发开去，课堂在学生的“再创造”学习活动中，形成一个强大的思维“碰撞场”和思想“交流场”，拓宽了思维的宽度。

教材是单薄的，也是丰满的，只有扎扎实实立足文本教材，吃透教材，科学地使用教材的情境、问题、插图、习题等资源，才能引导和帮助学生在创造数学中学习数学。