构建数学模型感悟数学魅力——《点表示数》教学案例

韦 莉

【教学内容】

浙教版五年级上册第114页。

【教学目标】

1.通过探究方格纸中点的不同位置，认识数的表示方法。

2.在观察、猜测、验证的学习过程中，培养学生有序思考的意识和推理概括能力。

3.在学与用的过程中，感受数学的神奇与魅力。

【教学重、难点】

感知不同位置表示的位值。

【教学过程】

一、揭示课题、尝试探索

师：今天我们一起来研究在方格里用点表示数。（板书）

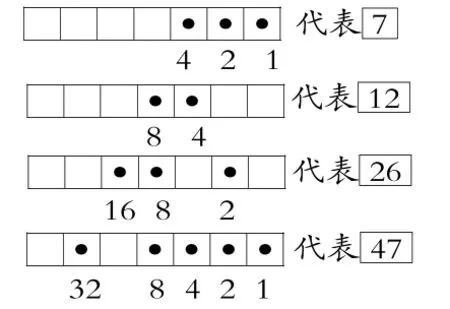
师：同学们请看，3应该怎么表示？

生：把点放在从右边数第三个格子表示3。

生：点在右边数的第1个格子代表1，点在右边数第2个格子代表2，在这两个格子里都放点就可以表示3了,因为1和2合起来是3。

师:其他同学和他想的一样吗？

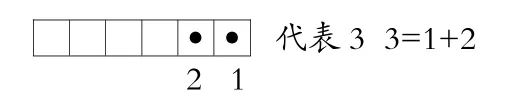
师：大家发现了么？从右起第1个格子放点代表1，在第2格放点代表2，这两个位置都放上点，合起来代表3。

【说明：参照教材直接出图，学生很容易受十进制计数法的影响看成“21”或“12”，很难和表示3联系起来。直接将问题“3应该怎么表示”抛给学生让他们思考，体现了两点：一是开放，学生猜想3是怎么表示的，他们有自己的想法，也得到了表达的机会。二是意外，学生的想法看似合理，但结果却出乎他们的意料。在经历了对计数法进行再创造的思考，学生的学习热情高涨，充满对新计数法探索的欲望。】

师：4可以怎样表示呢？

生：可以这样放点，从右边起，第1个格子放1个点，第2个格子放1个点，这样表示的是3，要表示4就得在第1格再放一个点。

生：可是一个格子只能放一个点！

生：我觉得在右边数第3个格子放1个点。

生：在右边第4格放点。

师：同学们对于4的表示方法，各有各的想法，你们觉得谁最有道理？我们先采用在右起第3个格放点来代表4的方法。等会儿再往下研究看看行不行。

【说明：让学生讨论“4”的表示，初步感知在“每格只能放1个点”的前提下怎样表示4更合适？实际上从右边起第1格和第2格都画上点时，能表示的最大的数是3，要表示4，就需要再往前一格，这是二进制中一次明显的“进位”，尽管这时很多学生尚未能感受到，而少数学生也只有模糊地感知，但这里的认知刺激已构成对新计数方法的猜想，指明了后续研究的方向和目标，是学生建构位值概念的起步。交流过程中，教师不急于介入引导，学生的思维品质在相互的交流碰撞中逐渐提升。】

师：观察1～4的表示方法，你有什么发现？

一个格子只能放1个点

生：我发现代表1是在从右往左第1个格子放1个点，代表2是在右往左第2个格子放1个点，但是代表3，就是在从右往左第1格和第2格各放上1个点，运用了加法，把它算出来了。

生：要代表某个数的话，可以是两个数的和，也可以在某个位置上放1个点。

师：同学们隐隐约约感觉到了在这些数的表示中只用1个点来表示哪几个数？

生：1、2、4。

师：而3是？

生：3得用1和2合起来表示。

生：我想问一个问题，如果“3”可以用加法表示，“4”那里能不能用加法来表示呢？

师：你们说呢？

生：不可以，因为2加2或1加3等于4，如果用1和3的话，1的位置就会重叠；如果用2加2的话，第2格就会重复。

师：谁还有补充？

生：像3这样可以用多个点相加来表示，不行的话，那些数就用一个点来表示。

师：这样的想法可不可行呢？接下来我们借助1、2、4这几个单点表示的数，看看能不能表示出其它的数。请你在练习纸上第1题，用铅笔画一画，写一写。

（学生独立完成，展示学生作业）

师：同学们，请停笔，眼睛看到大屏幕。让我们一起来听听他的想法。

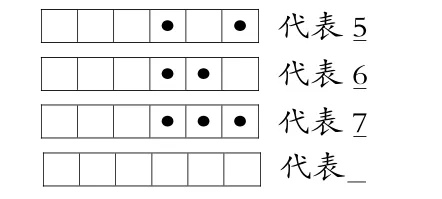
生：我觉得4加1表示5，所以在第3格画一个点，在第1格画一个点；4加2等于6，在第3格画一个点，在第2格画一个点；4加3等于7，所以在第3格画一个点，在第2格和第1格各画一个点，4加2加1是7。8的话应该是……

师：他不知道怎么表示8，有没有办法表示8？

生：我觉得，因为7用4、2、1来相加，7的下格就是8。

生：因为4加2加1表示7了，8呢只能是 4加 4，5加 3，7加1，如果这样的话那它都会有重叠，所以需要用另一个新格子表示8。

师：刚才咱们借助1、2、4表示出了5～7，在表示8的时候，同学们都发现了，右起3格子都填满的时候，最大只能表示几？

生：7。

师：我们要表示8，只能再往前1格，在右起第4格放点表示8。

师：现在回想一下，刚才咱们用右起3格的位置放点表示4，是不是有一些道理？

生：是。

【说明：“4为什么不能也像3那样用加法表示？”“怎样表示8？”这些问题的提出都反映出理解进制是难点。所以更要让学生去经历从产生困难到克服困难的过程，强化“1个格子只能放1个点子”、“需要新的格子表示”等等非常具象的二进制概念，感受计数单位的产生和扩展。在此基础上，教师引导明确：前面三格（即3个计数单位）都放点最多只能表示7，表示“8”的时候，要用一个新的格子（新的计数单位）来表示。再回应前面“4”的表示，学生对单位、进制的感知从朦胧到逐步清晰。】

师：从1～8的表示中(出示图)，你又有什么发现？

生：我发现用点代表的数，如果几个数相加能表示，就不用新的格子表示，如果几个数相加起来不能表示，就要用新的格子表示。

生：从1～8，能用加法的用加法，不能用加法的独占一格，用上新的格子，前面的这些点要全部去掉。

生：我发现，像前面比如说3填满了两格，4就要用第3格来表示，7填满了3格，8就要用第4格来表示。

生：我想强调一下：无论怎么加，它都会重复的话，就要新添一格来表示这个数。

【说明：有经历，还需有反思，才能形成经验、甚至是概括性的认识。鼓励学生基于个性化的理解，使用个性化的语言来评价和概括“用点表示数”的活动，从不同角度、不同认知层次来揭示新的计数方法的实质，包括位值、进制等等。】

师：那么从你们的发言中，是不是可以发现在这些数中，有些是特别重要的？

生：1、2、4、8。

师：既然这么重要，我们把它请出来，表示在黑板上。

师：想说什么？你来说。

生：我发现2是1的2倍，4是2的2倍，8是4的2倍。

生：我发现了每向右一格，表示的数都会乘2。

师：你们还有什么问题想提出来吗？

生：我想问，为什么有这样的规律呢？

师：会提问也是会学习的表现。

师：好，看来同学们都关注了这几个位置所表示的数以及它们之间的关系，有同学还提出了问题，猜想一下，右起下一个格子表示？

生：16。

师：你们怎么知道是16的？

生：8×2=16。

生：因为用前面这些数加起来：8+4+2+1=15，所以要新开一个数表示16。

师：是不是和你们想的一样呢？我们继续借助 1、2、4、8表示更多的数来试一试。

（学生介绍9～16的数的表示）

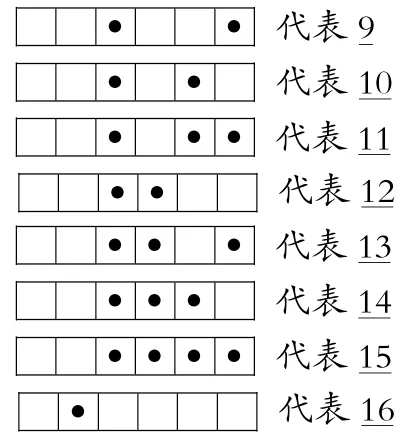
师：这样表示可以吗？不对的请改正过来。

师：现在1～16都在方格里用点表示出来了，对于这种用点表示数的方式你有什么认识吗？

生：一些数相加都不能得到一个数，就得重新开一格来表示。

生：从右往左，每一个格子表示的数都是乘2、乘2……

生：一些数是单个格子就能表示的，许多数是由多个格子加起来表示的。

生：我发现，新开一格的数，等于它右边所有格子表示的数相加再加上1。

师：如果继续往下，16左边这一格表示几？再左边一格？

生：32，64。

师：用点子在格子里可以表示这么多不同的数，点在不同的位置，表示不同的数。

二、学以致用，深化体验

师：根据刚才学到的用点表示数的方法，把答案写在方框里。

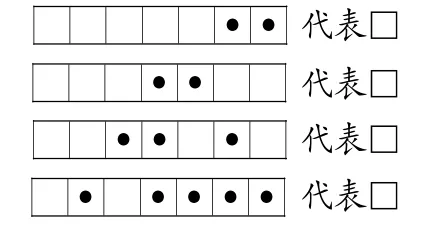
师：我看到你是第一个举手完成的，是不是有什么妙招？

生：一个一个格子加起来。根据上面表示数的方法，把答案写在□里。

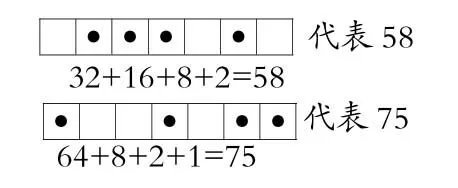
师：在格子里画点分别表示58和 75。

生：想能不能用64，超过58，然后用32加16，没有达到58，就加上8和2。

生：75，最大的 64，75-64=11，再找出最大的比它小的，11-8等于3，再找出最大的2，然后减去剩下1。

在格子里画点分别表示58、75。

三、总结反思、拓展提升

师：通过今天的学习，你有什么收获？

生：用点表示数，只要用白板 上 的 那 些 数（1、2、4、8、16……）。

生：用加法运算，可以表示出一个数。

师：谢谢同学们的分享，在方格里用点表示数，不同的位置可以表示不同的数。其实，在数的领域里，这样的想法也被广泛应用，计算机的运算就是不同通过把0和1放在不同的位置表示出不同的数来实现的。

（播放课件：如果格子里有点子，就记作1，没有就记作0。1就可以这样表示“1”，2可以这样表示“10”，继续出示表示 2、3、4……的二进制数，所有的数都可以用0和1这两个数来表示！）

师：很神奇吧！今天这节课我们就研究到这儿，谢谢同学们的参与，下课！