180°方形截面弯管内流动特性研究*

周 佳 朱目成 巫帅珍 罗月迎 贾传伟

(西南科技大学 制造过程测试技术教育部重点实验室)

180°方形截面弯管内流动特性研究*

周 佳*朱目成 巫帅珍 罗月迎 贾传伟

(西南科技大学 制造过程测试技术教育部重点实验室)

针对180°方形截面弯管内复杂的流动特性以及出现二次流现象等问题，运用Fluent软件对连续方程和纳维-斯托克斯方程进行空间离散，对180°方形截面弯管内的流动进行数值模拟计算。模拟计算结果与实验测量的结果基本相一致，说明建立的数学模型与数值方法是有效的。同时，分析了弯管内二次流形成与发展的现象，得出了二次流的变化规律。这为揭示180°方形弯管内复杂流动现象的作用机理提供了参考，对于机械设备的制造和应用具有一定的意义。

180°方形弯管 Fluent N-S方程 湍流 数值模拟 二次流

随着我国流体机械制造业的持续发展，弯管被广泛应用于如石油化工流体的输送、发电厂、水利、船舶和核电站冷却水循环系统等场合。弯管作为机械设备中的重要部件之一，在机械设备的设计、制造、使用和维护过程中都需要考虑弯管的流场特性对机械设备的影响。因此，研究弯曲管道内的流动特性具有一定的理论和工程实用价值。自20世纪20年代圆形截面弯管内二次涡流现象第一次被Dean W R提出后[1]，弯管内的二次流问题吸引了许多学者的研究[2，3]。Sudo K等采用旋转探针技术对90°圆形截面管道内的紊流流场经行研究，得出了雷诺应力等值线图、矢量图和轴向截面的速度等值线图[3]。Taylor A M K P使用LDV对90°弯曲管道内形成的湍流和层流进行了测量，得到了时均速度、脉动速度和壁面压力分布等实验数据[4]。江山等对90°圆形截面弯管内湍流流场经行了数值模拟，分析了二次流形成的原因，给出了二次流影响弯管内壁压力和速度分布的规律[5]。曾实和Manners A采用大涡模拟模拟了180°方形截面弯管的湍流流动[6]。徐俊等使用激光多谱勒测速仪完成了对180°弯管流场信息的实验测定[7]。

以往研究主要针对90°弯管内部流场进行测量和模拟，以及对180°弯管内部流场的测量，缺乏对180°方形截面弯管内湍流流场的研究分析，特别是二次流的详细分析。当前，随着现代科技的发展，数值模拟计算以其代价小、收效快的特点在科研方面占据的地位越来越重要，各种流体力学软件已被广泛应用在数值模拟计算领域[8]。笔者为研究180°方形截面弯管内的流动特性，使用Fluent流体计算软件，采用RNGk-ε湍流模型，对弯管内的湍流流动进行了模拟，得出详细的流场特性，重点考察流场速度和压力分布的变化规律以及弯管内横截面上产生二次流动现象。

1 物理模型

本文研究的物理模型为180°方形截面弯曲管道，其几何尺寸如图1所示。弯管的半径比为Rc/D=2.5，Rc=0.5(r1+r2)，方形截面边长D为100mm，左右两侧的直线段长度为500m，θ为极角，弯管开始弯曲截面为θ=0°，结束弯曲截面为θ=180°，弯曲内侧半径r1=200mm，外侧半径r2=300mm。

2 数学模型

2.1控制方程

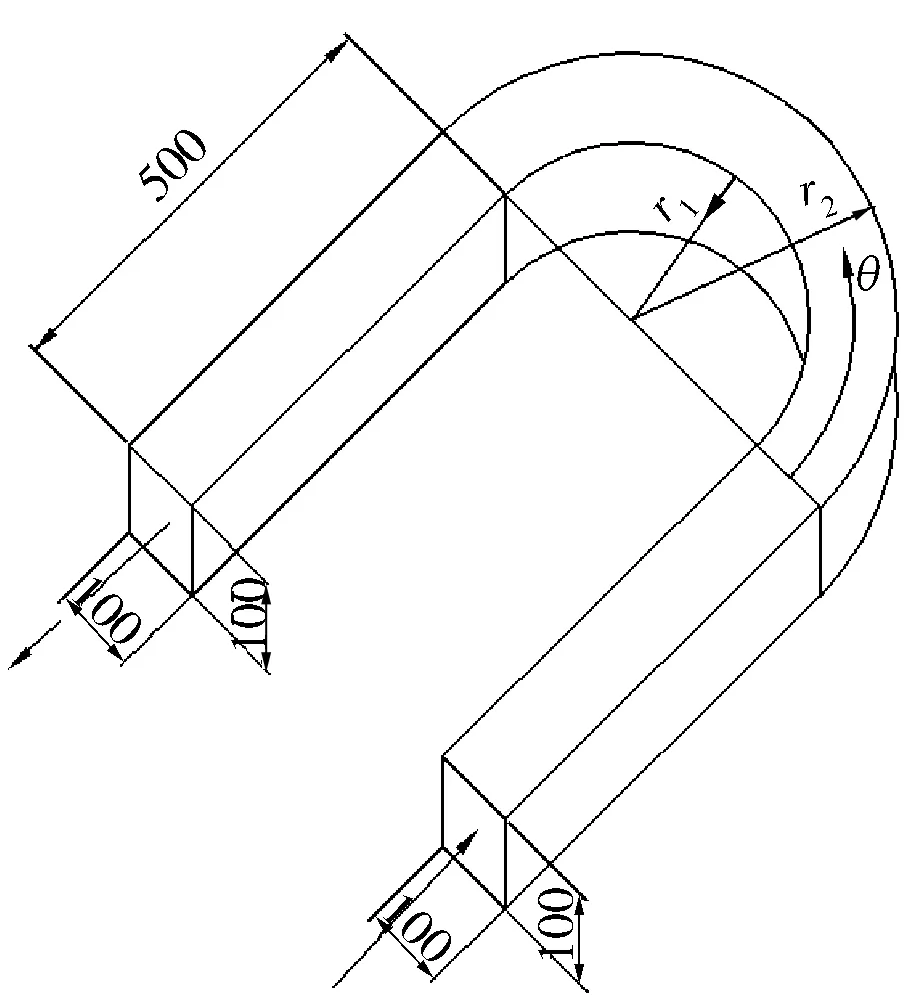
图1 180°方形截面弯管截面尺寸

通过对连续方程和瞬时纳维-斯托克斯方程进行时均化处理，得出在直角坐标系下的定常、绝热、不可压缩流体满足的控制方程：

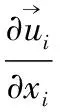
(1)

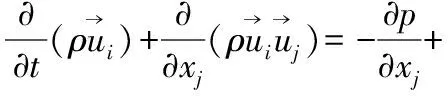
(2)

式中p——平均压强；

Si——源项；

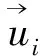
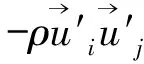
2.2RNGk-ε湍流模型

20世纪80年代，Yakhot V和Orszag S A在分析了以往研究者的成果以后，首次系统地运用RNG方法研究了湍流流场，提出在惯性子区域中湍流可用随机力作用下的纳维-斯托克斯方程描述[9]。该RNGk-ε模型既适用于高Re情况，也适用于低Re湍流的流动，提出了使用有效粘性系数的微分表达式，来描述低雷诺数情况的流动过程：

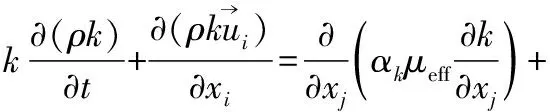
Gk-ρε

(3)

(4)

其中，αk、αε分别代表k、ε的反向有效Prandtl数，Gk代表由平均速度梯度引起的湍动能生成项。

S=(2SijSij)1/2

αk=αε=1.39,Cμ=0.085,C1ε=1.42,C2ε=1.68

ηo=4.377,β=0.012

文献[10]中对标准κ-ε、Realizableκ-ε和RNGk-ε模型进行了比较，认为RNGk-ε模型结合两层壁面模型的处理，可以有效地模拟大曲率影响弯管湍流流动的问题。

2.3网格划分和边界条件

利用Gambit前处理软件构建模型，Gambit中的求解器使用Fluent5/6，进口设定为velocity_inlet，出口设定为outflow。网格划分如图2所示。

图2 网格划分示意图

边界条件设置有：进口条件为流体的来流速度大小为13m/s，其方向垂直于弯管的纵向截面(XOY平面)；出口条件为采用自由出流条件；壁面条件为壁面上使用无滑移的边界条件。RNGk-ε模型适合于完全发展的湍流，用在湍流核心区域，但对壁面区域并不适用。采用标准壁面函数法作近壁面处理，可以提高计算效率，有利于工程的实用性，对于模拟各种壁面流动很有效[11]。

3 模拟计算结果与分析

3.1压力分布

将Gambit划分的网格输入至Fluent中，检查网格质量，变换单位，定义流体的物理性质，设置边界条件和初始条件。模拟计算得到弯管中心截面(Y=0)上的压力分布云图，如图3所示。

将XOZ平面不同角度径向方向上的压力模拟汇集在图4中。由图4可知，弯管中径向压力的变化是上升的。弯曲段部分，各截面相互间压力的变化较小。在0～60°截面，内侧压力逐步减小，而外侧压力逐步增大，在60°截面径向的压力梯度达到最大。从60～180°截面，内侧的压力逐步增大，外侧压力逐步减小。流体在0°和180°截面的径向压力变化曲率相近，且180°截面处的压力明显小于0°截面处的压力。

图3 管道中心截面压力分布

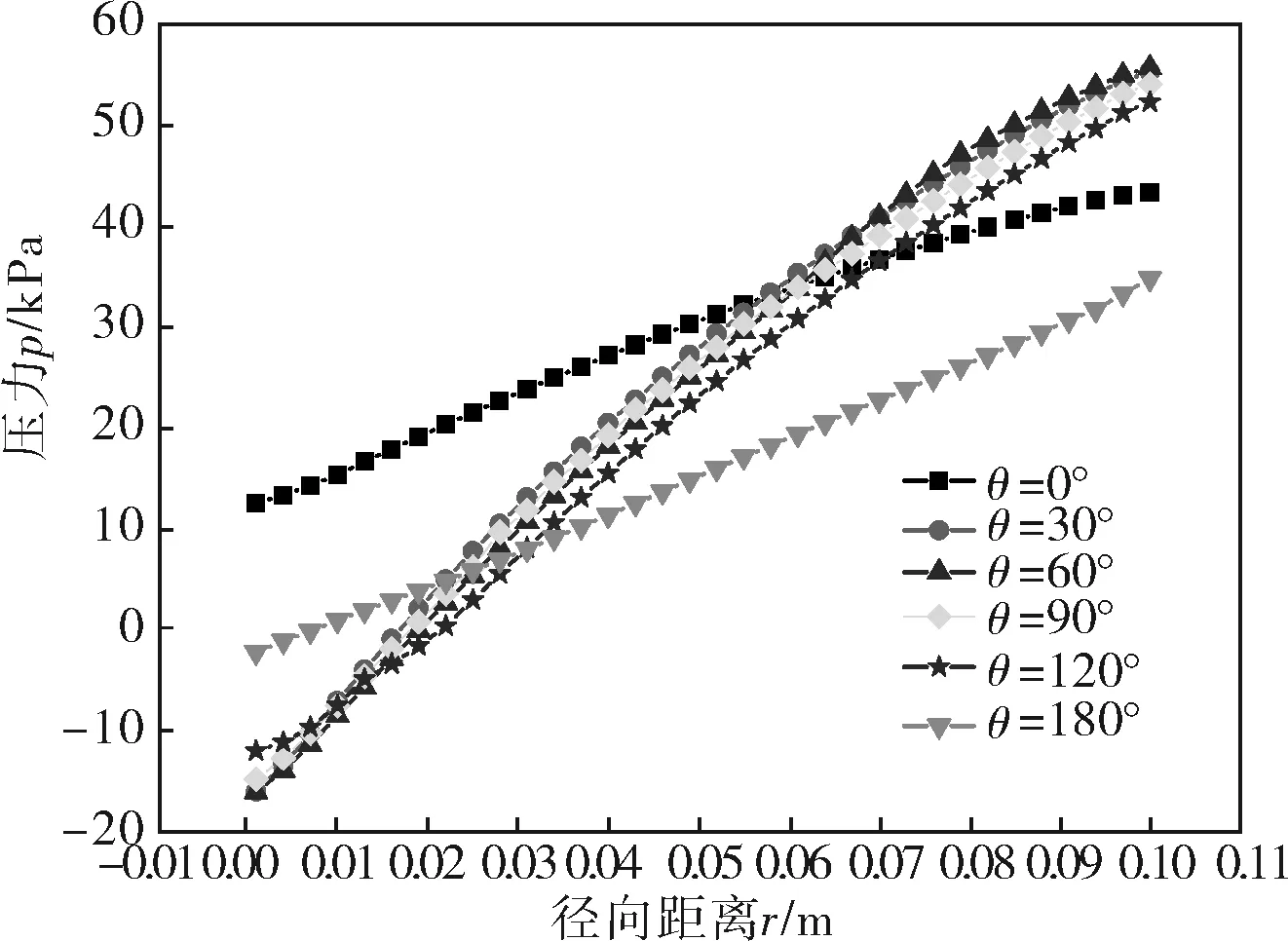
图4 径向压力分布曲线

从图3的压力分布云图也可观察到，在管道弯曲段内，沿着径向的压力梯度变化较大，内壁面附近压力较小，外壁面附近压力值较大的现象。这主要是因为流体在流动过程中受管道的弯曲作用，流体向曲率半径较大的外侧壁面流动，而使流体在外侧壁面挤压形成。弯管出口直管段的压力明显小于进口直管段处的压力，其原因是分子粘性致使流体沿管道壁面流动过程中产生的沿程损失和二次流的耗散。

3.2切向速度分布

流体在弯管内流动，速度变化主要是切向速度的变化。流体沿进口直管段进入弯曲部分后，由于受管道弯曲的作用，产生朝向外侧的离心力，而产生的离心力使得径向压力分布发生变化，呈现出径向压力梯度。

将弯管中心XOZ截面不同角度径向方向上的切向速度值模拟曲线汇集在图5中，可观察到：在0°截面，切向速度分布开始发生变化；在0～60°之间，内壁附近切向速度逐步升高，外壁附近的切向速度逐步降低。而流体在60°截面前后切向速度的变化则完全相反；在60～180°之间，内壁附近的切向速度逐步降低，外壁附近的切向速度逐步升高。流体在弯曲段受离心力的影响，内壁附近的切向速度明显大于外壁附近的切向速度；在180°截面内，弯管外壁附近的切向速度值很接近，但其值高于内侧切向速度值，且内壁面附近的切向速度值沿径向朝内侧减小较快。

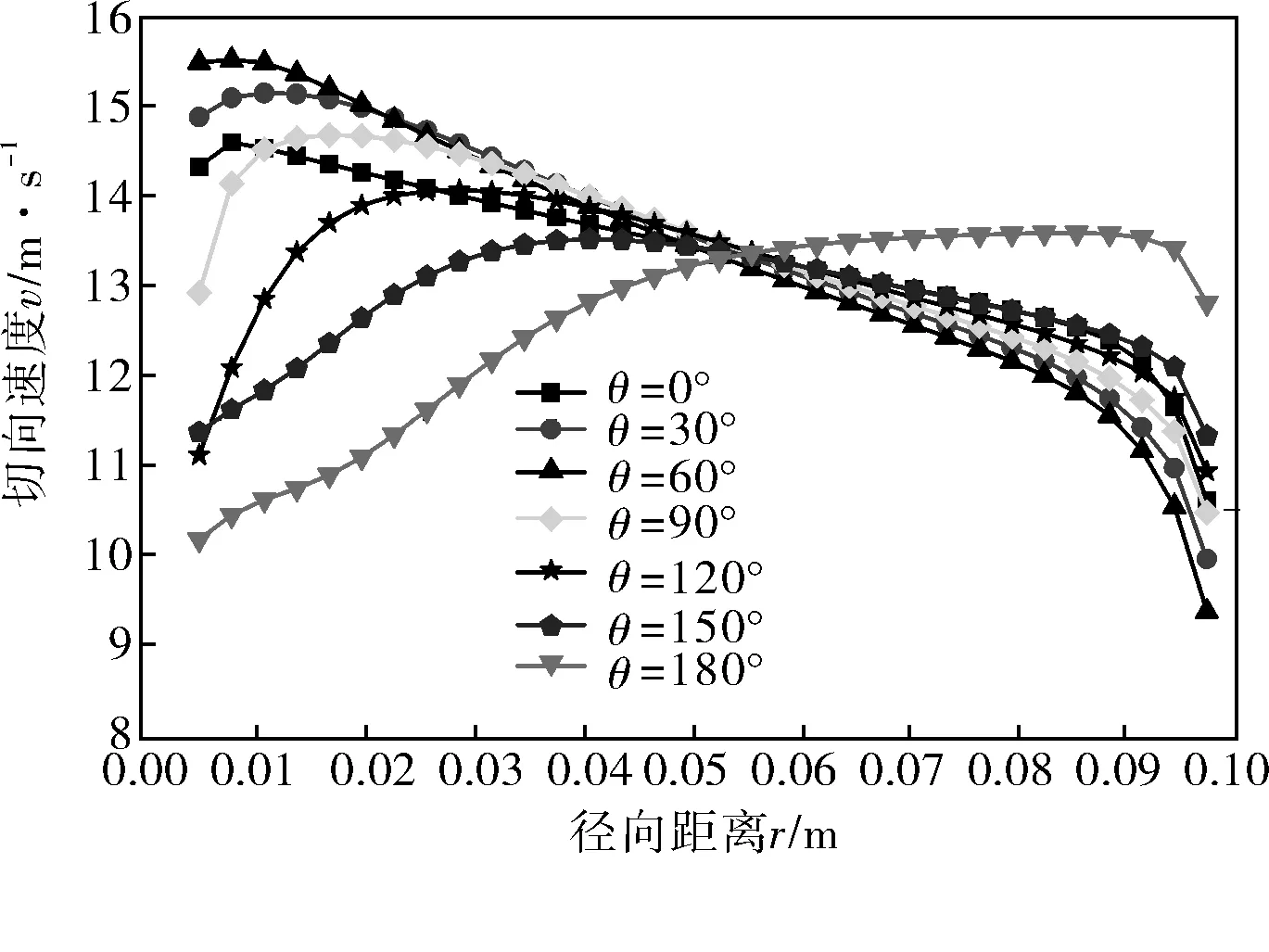
图5 切向速度分布曲线

流体在弯管的弯曲段，其内部速度和压力发生着复杂的变化。在0～60°间，外壁面附近压力升高，内壁面附近压力降低，而外壁面附近的切向速度降低，内壁面附近的切向速度升高。在流过60°截面附近以后，压力和速度发生相反的分布规律，外侧压力减小，内侧压力升高，而外侧切向速度升高，内侧切向速度减小。因此，数值模拟得出的数据与文献[7]用激光多普勒测速仪测量的实验结果基本一致。180°弯管内流场的压力和速度的分布规律与90°弯管相似，180°弯管其转折点在60°截面，90°弯管在30°截面[12]。

3.3二次流

180°方形截面弯管内的二次流是不可压缩粘性流体在管道流动的过程中，由于流体的粘性和离心作用在转弯处横截面上出现一对旋向相反的漩涡。沿主流方向弯管不同截面的速度矢量图如图6所示，可以看到180°方形截面弯管内垂直于主流的二次流的产生与发展过程。从θ=0°截面开始流体由直线流动向旋转流动转变，流体的径向速度指向内侧壁面。在θ=30°附近，外壁面附近的压力此时大于内壁面附近的压力，使得弯管中心的流体向外侧流动，外侧壁面附近上半部分的流体向上流动，下半部分的流体向下流动，且上下壁面附近的流体向内扩散，左上角和左下角出现较小的一对二次流。这种二次流漩涡推挤着面内的低速流体顺着主流不断向后发展。到θ=60°，二次流的旋转中心向弯管内侧移动。在θ=90°附近，强烈的二次涡流推挤内侧面附近的高速流体流过截面中心位置向外侧流动，上壁面和下壁面的低速流体由于二次涡流的带动，沿壁面向内侧面移动，此时截面上两个涡心继续向内侧壁面且相向移动，表明外侧压力大于内侧压力，使得流体向内侧移动。到θ=120°截面，二次流旋转中心仍然向内侧壁面和相向移动。在弯曲段θ=180°处二次流强度达到最大，二次流的旋转中心位于最内侧。

二次流的区域随着旋转流动从0°到180°逐渐扩大，强度增强。在出口直管段期间，二次流的涡心逐渐远离内侧向外侧移动，同时向弯管中间XOZ平面移动，二次流逐渐衰减直至消失。

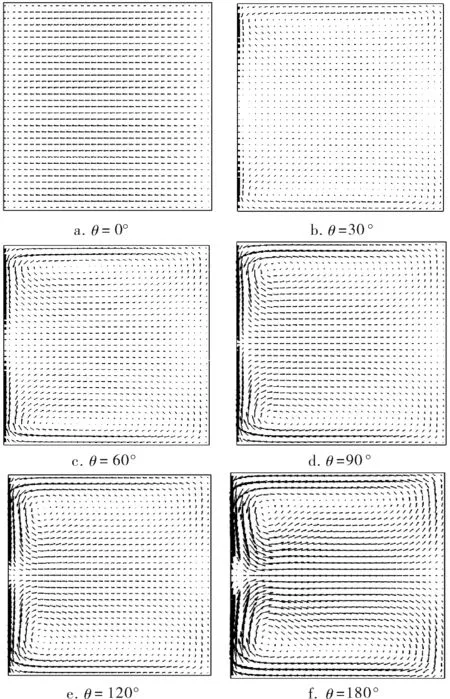
图6 沿主流方向弯管不同截面的速度矢量图

4 结束语

运用Fluent软件，完成对180°方形截面弯管内湍流流动的数值模拟计算，得到弯管内流场的变化规律。在整个弯曲段内，内侧压力低于外侧压力。在0～60°之间，外壁附近压力升高，切向速度减小，内壁附近压力降低，切向速度增大；在60～180°之间，外壁附近压力降低，切向速度增大，内壁附近压力升高，切向速度减小。同时，还重点分析了管道内二次流的形成和发展过程。这为揭示180°方形截面管道内复杂流动现象的作用机理提供了一定的借鉴。

[1] Dean W R.Note on the Motion of Fluid in a Curved Pipe[J].Phil Mag,1927,4(2):223～238.

[2] Azzola J.Developing Turbulent Flow in a U-bend of Circular Cross-Section[J].Journal of Fluids Engineering,1986,108(2):214～221.

[3] Sudo K,Sumida M,Hibara H.Experimental Investigation on Turbulent Flow in a Circular-Sectioned 90-Degree Bleed[J]. Experiments in Fluids,1998,25(1):42～29.

[4] Taylor A M K P,Whitelaw J H,Yianneskis M.Curved Ducts with Strong Secondary Motion: Velocity Measurements of Developing Laminar and Turbulent Flow [J].Journal of Fluids Engineering,1982, 104(3):350～359.

[5] 江山,张京伟,吴崇健,等.基于FLUENT的90°圆形弯管内部流场分析[J].中国舰船研究,2008,3(1):37～41.

[6] 曾实,Manners A.180°方形弯管中湍流流动的大涡模拟[J].清华大学学报(自然科学版),1999,39(4):100～103.

[7] 徐俊,杜彩虹,王甜,等.180°矩形弯管流场的LDV测量[J].实验流体力学,2010,24(1):36～41.

[8] 谢俊,郭洪锍,陈炜,等.基于ANSYS和Fluent软件的导流管流场分析[J].机械设计与制造,2008,9(9):70～72.

[9] Yakhot V, Orszag S A.Renormalization Group Analysis of Turbulence 1.Basic Theory [J].Journal of Scientific Computing, 1986,1(1):39～51.

[10] 丁珏,翁培奋.三种湍流模式数值模拟直角弯管内三维分离流动的比较[J].计算物理,2003,20(5):386～390.

[11] 王福军.计算流体动力学分析[M].北京:清华大学出版社，2004.

[12] 尚虹,王尚锦,席光,等.90°圆截面弯管内三维紊流场实验研究[J].航空动力学报,1994,9(3):263～266.

ResearchonInnerFlowCharacteristicsof180°ElbowPipeswithSquareSection

ZHOU Jia, ZHU Mu-cheng, WU Shuai-zhen, LUO Yue-ying, JIA Chuan-wei
(SchoolofManufacturingScience&Engineering,SouthwestUniversityofScience&Technology,Mianyang621010,China)

Aiming at the complex flow characteristics and the secondary flow phenomenon in 180° elbow pipe with square section, the Fluent software was adopted to implement spatial dispersion of continuous equation and Navier-Stokes equation and to simulate and calculate turbulent flow in this 180° elbow pipe. The simulation result shows that this calculation result coincides with the experimental result; and it indicates that both established mathematical model and numerical method are effective; meanwhile, the formation and development of the secondary flow within the elbow pipe were analyzed to obtain the change rules of this secondary flow so as to provide the reference for revealing the mechanism of complex flow in the 180° elbow pipe with square section, and it has a certain significance for both manufacturing and application of mechanical equipment.

180° elbow pipe with square section, Fluent, N-S equation, turbulence flow, numerical simulation, secondary flow

* 国家科技支撑计划资助项目(2014BAF12B05)。

** 周 佳，男，1990年9月生，硕士研究生。四川省绵阳市，621010。

TQ055.8

A

0254-6094(2016)02-0214-05

2015-06-19)