线性代数教学主线研究

彭司萍，龙正平

（火箭军工程大学 理学院，陕西 西安 710025）

线性代数教学主线研究

彭司萍，龙正平

（火箭军工程大学 理学院，陕西 西安 710025）

分析了线性代数教学现状，从不同角度对线性代数的教学主线进行了探索研究.举例说明在线性代数教学过程中重视对教学主线的研究，是化解教学难点，提高教学质量的有效途径.

线性代数；教学主线；教学难点

线性代数作为数学的一个分支，主要研究有限维线性空间的线性理论与方法，它秉承了一般代数学的实用性、抽象性和高度思辨性的特点.随着现代科学技术的迅猛发展，特别是计算机技术在工程问题线性化建模与离散数据处理方面的广泛应用，使得线性代数逐渐成为科技工作者不可或缺的数学工具，它也因此成为经济类和理工类学生要求掌握的一门重要基础理论课程.

1 线性代数教学现状分析

目前，为非数学专业学生开设的线性代数大体上包括以下几部分内容：行列式、矩阵、线性方程组、线性相关性、二次型、线性空间与线性变换.通过这些内容的学习，不仅可以使学生掌握一些有用的运算工具和算法，更为重要的是可以使学生的逻辑思维能力、运算能力、抽象及分析综合能力得到严格训练，帮助学生构建起一种崭新的思维模式，这种思维模式对一个人能力与灵魂的培养和塑造，往往比学习代数知识本身更具有时效性、理喻性、拓展性和实用性，甚至可以影响一个人的一生［1］.然而由于种种原因，当前线性代数却已成为高等工科院校中的一门难教、难学的基础理论课程［2-4］，抛开抽象性强、学时少、学生知识储备不够等原因，线性代数知识体系自身特点和它独特的思维模式是造成这种难教、难学现状的主要原因.这主要是由于线性代数的知识体系在表现形式上是一个个独立的“块状”，而线性代数的思维模式却是以“集成化”为基本特征，即使用“集成化元素”（向量、矩阵、行列式、多元方程组、空间与子空间）、采用多元整合的方式解决多元问题.线性代数在内容的描述方式上既有代数模式（即使用代数语言进行描述，如矩阵和变换等），又有几何模式（即使用几何语言进行描述，如向量和空间等），2种模式对应2种思维形式，即分析思维形式和空间思维形式［5］，学习线性代数需要时时转换思维形式，对于学生而言这也是学好本门课程的一个难点所在.

因此，知识体系构成的独立性和思维模式的集成化、多样化之间的矛盾是当前影响线性代数教学质量的一个重要原因.为了化解这种矛盾，教师在教学过程中，应当注意把握一条主线，将各个孤立的“块状”知识联接起来，串成一个统一、有序的有机整体，使学生在学习过程中能够清楚各个环节的来龙去脉和前因后果，解决问题时也就灵活自如了.

2 线性代数教学主线研究

从现有文献资料来看，对线性代数教学主线的研究并不多［6］.结合多年的教学经验，尝试从不同角度对线性代数的教学主线进行阐述，包括问题主线、关联主线和方法主线.

2.1 问题主线

线性方程组是线性代数的一个重要研究对象，主要包括线性方程组解的存在性和线性方程组解的结构.以同济大学的《线性代数》［7］教材为例，考察线性代数各章的内容，不难发现它们都涉及到线性方程组，或者说都与线性方程组的求解有关.因此，线性方程组的求解可以看作是本课程教学的一个主题和主线，它将各个孤立的“块状”知识联接起来.

虽然各个知识块都是为线性方程组的求解服务，但是从知识体系的编排来看，它们的地位和作用是不同的.具体来说整个教学过程可以分解为如下步骤：（1）提出问题.生产生活中的许多问题都可以转化为线性方程组的求解问题，即如何解线性方程组.（2）对于一些简单、特殊的线性方程组，可以利用行列式即借助克拉默法则进行求解，但这种方法存在局限性.只有当方程个数与未知量个数相等，并且系数行列式不等于零时才可行.因此，需要考虑如何求解一般的线性方程组.（3）通过对高斯消元法和矩阵初等行变换的比较，发现线性方程组的求解都可以归结为对增广矩阵的初等行变换，于是得到求解一般线性方程组的方法——矩阵的初等变换法.但当线性方程组的解不唯一时，不同的人得到的解的形式往往不同.因此，需考虑在无穷多个解中，解与解之间是否有关系，能否给出解的统一表达式.（4）在对向量组的线性相关性和线性表示研究过程中可以看出，向量组的线性相关、线性表示其实质就是讨论齐次线性方程组和非齐次线性方程组的解的问题，于是进一步得到线性方程组解的结构的表达式.至此，线性方程组的求解问题就已经全部解决.转而讨论线性方程组理论和方法的综合运用，这就是第五章的知识.第六章对非数学专

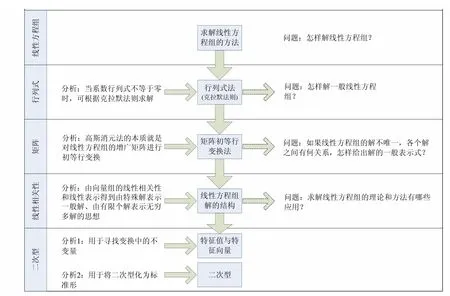
图1 问题主线

问题主线的优点是由浅入深、环环相扣，以问题牵引教学，符合学生的认知规律，有利于激发学生的学习兴趣.按问题主线组织教学需要注意以下几个问题：一是从一个知识块向另外一个知识块过渡的时候，所设置的问题应该能起到承上启下的作用，并且难度恰到好处；二是要求学生紧跟教师的教学进度，对每一个知识块的基本概念、基本方法以及已经解决的问题、还存在的问题都熟练掌握.

2.2 关联主线

在为工科学生开设的线性代数课程中，向量组的线性相关性是这一课程的难点和重点.由于它是对向量组一般性质的研究，抽象性很强，学生学习起来感觉有困难，而它的重要性在于本课程的所有内容都与线性相关性存在关联（见图2）.

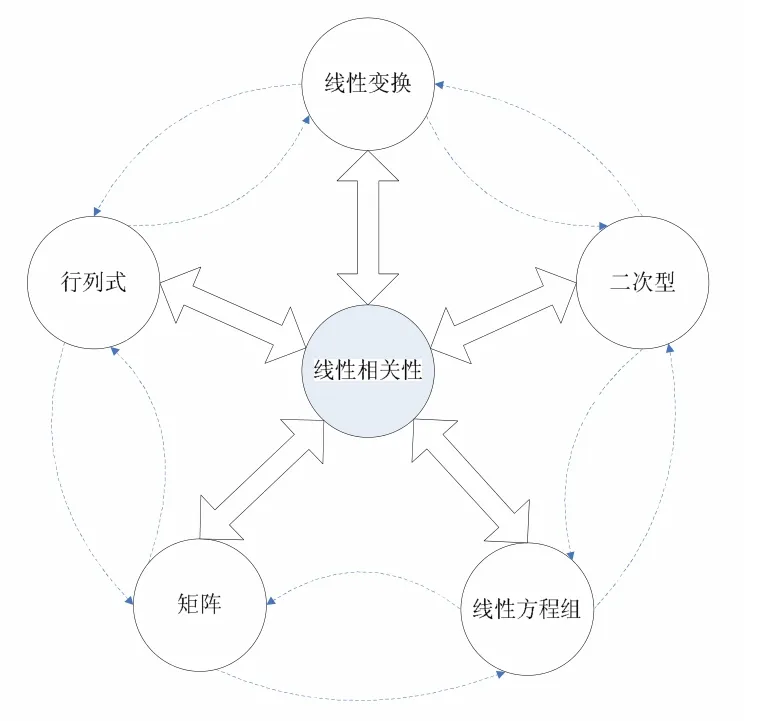
图2 关联主线

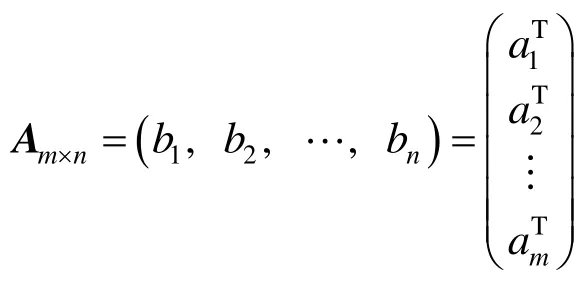
知识块之间的这种关联性就像一张网，将整个线性代数的知识体系包络其中，形成一个既相互独立又彼此关联的有机整体.按照关联主线组织教学有助于培养学生的发散思维，达到融会贯通的效果.但是，要在教学过程中让学生理解和掌握这种关联性不是一件容易的事情，只有当整个课程都学习完了之后，通过对课程的梳理和总结，才可能让学生感受到这种关联性的美妙.

2.3 方法主线

历史上，矩阵是在研究线性方程组的解时产生的一个重要概念，到如今矩阵理论已经成为研究线性代数的一个主要工具，因此有线性代数是一门“空间为体，矩阵为用”［3］32的课程的说法，即矩阵是处理向量空间及其线性变换的工具.考察整个线性代数知识体系，不难发现所有内容都可以用矩阵及矩阵的运算来表示和研究.因此，以矩阵理论为中心可以建立起一条线性代数教学的方法主线（见图3）.图3中实箭头指向表示矩阵理论的基本应用方向，而虚箭头指向则表示相应理论在矩阵理论研究中的应用.

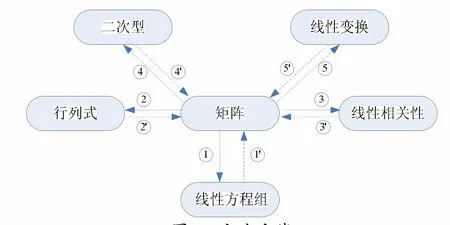
图3 方法主线

各组箭头的具体含义如下：

第1组箭头：首先，线性方程组可以表示为矩阵方程的形式Ax=b（b=0时为齐次线性方程组，b≠0时为非齐次线性方程组）；其次，可以利用系数矩阵A和增广矩阵(A, b)秩的关系研究线性方程组是否有解，有多少解；最后，还可以利用矩阵的初等行变换法求解线性方程组.反过来，根据解的情况可以推断出相关矩阵的关系和秩的情况，还可以利用线性方程组解的性质解释矩阵运算的某些性质.

第3组箭头：由于矩阵的秩等于其行（列）向量组的秩，因此可以利用矩阵来研究向量组的线性相关性和线性无关性；向量可看成是特殊的矩阵，因此向量和矩阵拥有相同的线性运算法则.反过来，矩阵也可以看作是有限个有限维列（行）向量组成的向量组，从向量组的线性相关性可以得到矩阵秩的信息.

方法主线能使学生清楚看到矩阵理论在线性代数研究中的应用，有助于发现问题的本质，从而找到解决问题的途径和方法.特别是随着计算机技术的迅猛发展，一些以矩阵为运算单元的软件（如MATLAB）的广泛使用，使得矩阵这一工具在理论研究和工程实际中扮演着越来越重要的角色.

行列式和矩阵是求解线性方程组有效工具和方法，但若熟练掌握线性代数的教学主线，不难发现也可以通过构造特定的线性方程组来解决行列式和矩阵的一些问题.

例［8］设n阶矩阵A的伴随矩阵为A*，证明：若，则.

一般教学辅导书中都是采用反证法证明的，本文通过构造线性方程组，利用线性方程组解的存在定理（关于线性方程组解的存在性的2个定理）给出证明.

在线性代数教学过程中注意把握教学主线，不仅可以化解教学难点、打通知识关联，帮助学生建立全局的而不是局部的、系统的而不是孤立的知识概念图，而且对学生的数学思维训练和综合能力的提高具有重要的意义.

［1］ 范新华.21世纪线性代数课程建设与教学改革的探索［J］.常州工学院学报，2005，18（2）：75-78

［2］ 杜建卫.让线性代数课程易教易学［J］.大学数学，2011，27（5）：179-184

［3］ 李尚志.线性代数教学改革漫谈［J］.教育与现代化，2004（1）：30-33

［4］ 周玲.《线性代数》课程教学点滴谈［J］.大学数学，2005，21（1）：30-32

［5］ 孙名符.数学·逻辑与教育［M］.北京：高等教育出版社，1994：201-206

［6］ 陈丽，白金诺.线性代数的主线及核心应用［M］.北京：高等教育出版社，2012（10）：8-11

［7］ 同济大学数学系.工程数学·线性代数［M］.5版.北京：高等教育出版社，2009

［8］ 彭司萍，龙正平.线性方程组在行列式和矩阵计算中的应用［J］.高师理科学刊，2015，35（12）：27-30

Discussion on the main teaching line of linear algebra

PENG Si-ping，LONG Zheng-ping
（School of Science，The Rocket Army Engineering University，Xi'an 710025，China）

A deep analysis of the linear algebra teaching situation is made，some useful ideas for the main teaching line of linear algebra from different perspectives are provided.Several examples are given to illustrate that paying attention to the main teaching line in the linear algebra teaching is an effective way to solve the difficulties and improve the teaching quality.

linear algebra；main teaching line；teaching difficult points

O172.2∶G642.0

A

10.3969/j.issn.1007-9831.2016.06.023

1007-9831（2016）06-0075-05

2016-03-02

彭司萍（1979-），女，湖南保靖人，讲师，硕士，从事大学数学教育研究.E-mail：pengsip@126.com