混合变分不等式的变分原理
黄冬梅
(西华师范大学 数学与信息学院,四川 南充 637009)
混合变分不等式的变分原理
黄冬梅
(西华师范大学 数学与信息学院,四川 南充 637009)
描述并分析了有限维空间中混合变分不等式的变分原理,同时给出了混合变分不等式的解基于鞍点的刻画,最后,针对一些特殊情型给出了混合变分不等式问题基于经典优化问题的等价性刻画。因为线性,非线性补问题也可纳入混合变分不等式问题的框架,所以文章中得到的结果也可以直接用于这类问题。
变分不等式;混合变分不等式;变分原理
0 引 言
混合变分不等式是Duvaut与Lions在文献[1]中引入的,
〈F(x),y-x〉+f(y)-f(x)≥0,∀y∈K,
(1)

1 预备知识
为了描述问题(1)的变分原理,先介绍一些凸分析中的基本概念和结果[6,7]。


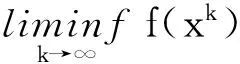

定义的函数δK称为K的示性函数。由δK的定义,可以验证δK是一个闭正常凸函数而且domδK=K。
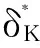
f(y)-f(x)≥〈ξ,y-x〉
则称ξ为凸函数f在点x处的次梯度。一般来说,在某点处的次梯度未必只有一个,将f在点x处的全体次梯度构成的集合记为∂f(x),并称之为f在点x处的次微分。


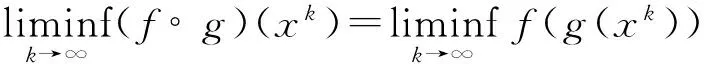
这表明,x∈levf(f∘g,β),即f∘g下半连续。

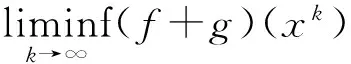
即f+g是闭的。
凸函数的次微分与共轭函数之间有着如下的联系[6,7]。

此外,若f为闭正常凸函数,则ξ∈∂f(x)也等价于x∈∂f*(ξ)。
有了上述准备, 可以将混合不等式问题(1)的解与函数次微分之间联系起来。

证明 先证充分性。由于K为闭凸集,δK为闭正常凸函数,又由于f也为闭正常凸函数,且domf∩K≠Ø,利用引理1,f+δK也为闭正常凸函数。假设-F(x)∈∂(f+IK)(x),则

(f+δK)(y)-(f+δK)(x)≥〈-F(x),y-x〉。
(2)
特别地,取y∈domf∩K,则上式变为
f(y)-(f+δK)(x)≥〈-F(x),y-x〉,
这表明x∈K。在(1)中取y∈K,则有
f(y)-f(x)≥〈-F(x),y-x〉,∀y∈K,
也即
〈F(x),y-x〉+f(y)-f(x)≥0,∀y∈K。
这样,x是混合变分不等式问题(1)的解。
再证必要性,假设x∈K是混合变分不等式问题(1)的解,则对任意的y∈K,有
〈F(x),y-x〉+f(y)-f(x)≥0,
从而


(f+δK)(y)-(f+δK)(x)≥〈-F(x),y-x〉。
由次梯度的定义,有-F(x)∈∂(f+δK)(x)。
2 混合变分不等式问题的变分原理

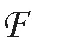
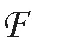
(3)
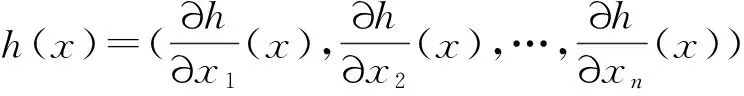
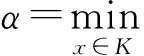
(4)
我们有如下的结果:

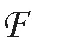
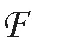
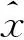


(f+h+δK)(x)+(f+h+δK)*(ξ)≥〈ξ,x〉。
(5)
特别地,任取ξ=▽h(x)-F(x)及x∈K,有
f(x)+h(x)+(f+h+δK)*(▽h(x)-F(x))≥〈▽h(x)-F(x),x〉,
(6)
即是
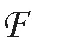
(7)
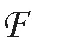
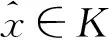

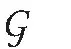
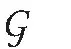
(8)
其中h如(3)所定义。
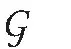
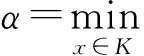
(9)
我们有如下的结论:

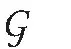
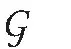
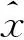

(h+δK)(x)+(h+δK)*(ξ)≥〈x,ξ〉。
(10)
由于domf∩domh∩K≠Ø,特别地,任取ξ=-F(x)-▽f(x)+▽h(x)及x∈K,有
h(x)+(h+δk)*(-F(x)-▽f(x)+▽h(x))≥〈x,-F(x)-▽f(x))+▽h(x)〉,
从而
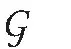
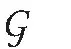
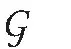
由于f,h在包含K的某个开邻域上连续可微, 由次微分定义有
∂h(x)={▽h(x)},∂f(x)={▽f(x)}。
从而有
-F(x)∈∂(f+δK)(x)。
由引理2,知x是混合变分不等式(1)的解。
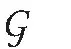
(3)证明与定理1对应结果的证明类似。
3 混合变分不等式的解与鞍点
在本节中,K,f,h与前面一样且K⊆domf∩domh。为了引入与定理1中的变分原理相对应的对偶变分原理,定义L1∶K×K→(-∞,+∞)如下:
L1(x,y)=〈y-x,▽h(x)-F(x)〉+f(x)-f(y)+h(x)-h(y)。
(11)
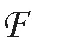
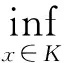
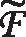
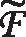
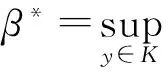
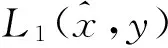

当f在包含K的某个邻域上连续可微时,下面引入与定理2中的变分原理相对应的对偶变分原理。定义L2∶K×K→(-∞,+∞)
L2(x,y)=〈F(x)+▽f(x)-▽h(x),x-y〉+h(x)-h(y)。
(12)
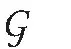
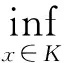
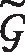
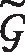
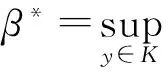
且有与定理3类似的如下结果。

证明 与定理3的证明类似。
4 例子
本节将给出第3节中关于变分不等式(1)变分原理应用的一些具体例子。
例1 设混合变分不等式(1)中的K是一个闭凸集,f在包含K的某个开邻域上连续可微,则在(8)中取h(x)≡0,有
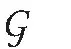
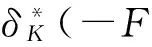
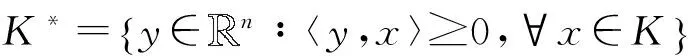
F(x)+▽f(x)∈K*,〈F(x)+▽f(x),x〉=0。
当然,它们也都等价于如下的最小值问题
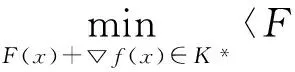
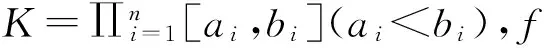
在(8)中令h≡0,x∈K,由定理2,混合变分不等式问题(1)等价于求如下函数的最小值问题
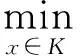
[1] DUVAUT G,LIONS J.Les inequations en mechanique et en physique[M].Paris:Dunod,1972.
[2] HE Y R.A new projection algorithm for mixed variational inequalities (in Chinese)[J].Acta Math.Sci.2007,27A(2):215-220.
[3] HAN W M,REDDY B D.On the finite element method for mixed variational inequalities arising in elastoplasticity[J].SIAM J. Numer.Anal.1995,32(6):1778-1807.
[4] XIA F Q,HUANG N J,LIU Z B.A projected subgradient method for solving generalized mixed variational inequalities[J].Oper.Res.Lett.2008,36(5):637-642.
[5] AUCHMUTY G.Variational principles for variational inequalities[J].Numer.Funct.Anal.and Optim.1989,10(9/10):863-874.
[6] FUKUSHIMA M.Theory of Nonlinear Optimization (in Japanese)[M].Tokyo:Sangyo Tosho,Inc.,1980.
[7] ZEIDLER E.Nonlinear functional analysis and its applications,III variational methods and optimization[M].Springer Verlag,1985.
[8] WU K Q,HUANG N J.The generalised f-projection operator with an application[J].Bull. Austral.Math.Soc.,2006,73(2):307-317.
[9] FACCHINEI F,PANG J S.Finite-Dimensional Variational Inequalities and complementarity problems[M].New York:Springer-Verlag,2003.
[10] AUCHMUTY G.Duality for nonconvex variational principles[J].J.Differential Equations.1983,50(1):80-145.
Variational Principles for Mixed Variational Inequalities
HUANG Dongmei
(College of Mathematic and Information,China West Normal University,Nanchong Sichuan 637002,China)
The theory of mixed variational inequality problems has wide applications in economics,finance,optimization and game theory.This paper describes and analyzes variational principles for the solution of mixed variational inequalities on closed convex sets in finite dimensional Euclidean spaces.A saddle point characterization of the solution is also given.Some special cases are also given to illustrate mixed variational inequalities.Since linear,and nonlinear complementarity problems may be framed as mixed variational inequalities,this theory also applies to such problems.
variational inequality;mixed variational inequality;variational principle
1673-5072(2016)03-0297-06
2015-12-26 基金项目:国家自然科学基金项目(11371015);教育部科学技术重点项目(211163);四川省青年科技基金(2012JQ0035)
黄冬梅(1980—) , 女, 湖北荆州人,讲师,主要从事优化理论及应用研究。
黄冬梅,E-mail: huangdmmath@163.com
O221
A
10.16246/j.issn.1673-5072.2016.03.012

