基座弹性影响下空间站柔性关节机械臂的鲁棒自适应滑模控制及双重弹性振动主动抑制
梁 捷,陈 力,梁武林,秦开宇
(1.电子科技大学航空航天学院,成都611731;2.福州大学机械工程及自动化学院,福州350108;3.中国空气动力研究与发展中心,绵阳621000)
基座弹性影响下空间站柔性关节机械臂的鲁棒自适应滑模控制及双重弹性振动主动抑制
梁 捷1,3,陈 力2,梁武林3,秦开宇1
(1.电子科技大学航空航天学院,成都611731;2.福州大学机械工程及自动化学院,福州350108;3.中国空气动力研究与发展中心,绵阳621000)
讨论了基座存在弹性情况下,载体位置、姿态均不控的空间站柔性关节机械臂系统控制问题。利用拉格朗日方法结合动量守恒定律,建立了弹性基座空间站柔性关节机械臂系统动力学方程。以此为基础,依据级联控制法,将系统分解为弹性基座刚性臂子系统和关节柔性电机转子子系统。对于弹性基座刚性臂子系统,为了主动抑制弹性基座柔性振动,运用虚拟力的概念,构造同时反映柔性模态和刚性运动轨迹的混合期望轨迹,通过改造原有的控制方案,提出基于虚拟力概念的鲁棒自适应滑模控制器控制策略,由于运用了虚拟力的概念,从而仅通过设计一个控制输入便可同时保证刚性轨迹跟踪并对载体基座的弹性振动进行主动抑制,更适应于空间站柔性关节机械臂系统的实际应用。同时,针对系统参数未知的情况,利用级联控制方法能够有效地抑制柔性关节的振动。理论分析及仿真算例均表明了控制方法的可行性。
空间站;柔性关节机械臂;弹性基座;动力学建模;鲁棒自适应滑模控制;弹性振动主动控制
1 引言
自20世纪80年代以来,美国、日本、加拿大、欧空局等国家和地区大力发展空间机械臂技术,相继发射试验卫星进行了各种试验[1⁃6]。机械臂是辅助完成飞行器空间对接、目标搬运等操作的重要工具[7⁃8]。目前,针对各种工况下不同类型的空间机械臂系统,科研人员对其控制问题已经做了大量的研究工作,取得了一系列成果[9⁃12]。近年来,随着对空间操控精度要求的不断提高,空间机械臂在作业过程中所呈现出来的各类柔性效应已逐渐被人们所察觉[13⁃14]。对于这些具有浮动载体基座和柔性部件的空间机械臂而言,动力学的非完整性及系统刚、柔性运动间的强耦合性将大大增加其动力学分析的难度,并给后续控制方案的设计带来障碍。我们注意到,目前有关柔性空间机械臂的研究文献多数谈及的是臂杆柔性[15⁃17],部分涉及关节柔性[18],但很少计及载体基座的柔性,而同时兼顾基座柔性和关节柔性的研究文献更是鲜有报导。
早期对机械臂控制研究不成熟时,只能采取减缓机械臂运动速度的方法来降低导轨振动[19]。如今随着空间技术的发展和对机械臂工作要求的提高,美国航天局和加拿大航天局开始评估基座弹性对机械臂末端爪手运动的影响,并研究了相应的控制方案[20]。显然,较以往仅带有柔性关节或弹性基座的空间站机械臂,具有弹性基座的柔性关节空间站机械臂具有更强的非线性及强耦合性,其动力学分析将更复杂,且难以直接选用先前各类常规的控制策略。因此有必要开展在系统非完整约束、基座与关节柔性并存下漂浮基空间站机械臂的动力学建模与控制问题研究。
本文将级联系统法和虚拟力概念应用到弹性基座空间站柔性关节机械臂控制器设计中,拟解决机械臂载体姿态及关节角的轨迹跟踪问题,同时主动抑制载体基座的弹性振动及关节柔性振动。依据级联控制法,将系统分解为弹性基座刚性臂子系统和关节柔性电机转子子系统。对于弹性基座刚性臂子系统,为了主动抑制弹性基座柔性振动,运用虚拟力的概念,构造同时反映柔性模态和刚性运动轨迹的混合期望轨迹,通过改造原有控制方案,提出基于虚拟力概念的鲁棒自适应滑模控制策略,以实现机械臂的载体姿态及关节角的轨迹跟踪同时主动抑制载体基座的弹性振动。
2 基座弹性影响下漂浮基空间站柔性关节机械臂系统动力学建模
机械臂是完成辅助对接、目标搬运等操作的重要工具。文中重点研究基座弹性影响下空间站柔性关节机械臂系统的控制方案,研究内容来自大型舱外空间机器人,以“加拿大二号臂”为例[21]:它于2001年首次在国际空间站上投入使用,官方名称为空间站远距离机械手系统(Space Station Remote Manipulator System,SSRMS),与移动基座系统、专用灵巧机械手组成移动维修系统(Mobile Servicing System,MSS)。空间站机械臂安装在桁架组装而成的导轨上,受动力学特性约束,空间站机械臂在工作过程中与空间站本体存在强耦合作用,易使与移动基座连接的导轨发生振动,影响末端轨迹跟踪精度[22]。该文对导轨存在弹性振动(本文称之为基座弹性影响)的空间站柔性关节机械臂进行动力学控制研究,与本文研究对象相似,因此本文选择图1所示机械臂作为分析模型,它由机械臂载体(空间站)、两杆刚性机械臂、两个柔性关节铰和移动导轨组成。
不失一般性,以做平面运动且载体位姿不受控制、具有弹性基座的关节柔性空间站机械臂系统为例,进行系统动力学分析,系统物理模型如图2所示。该系统由自由漂浮的空间站载体W0、两个弹性关节Oi(i=1,2)和两个刚性机械臂W1、W2及W2末端爪手抓持着的刚性载荷WP组成。

图1 基座存在弹性的空间站柔性关节机械臂Fig.1 Flexible joint manipulator of the space station with elastic foundation
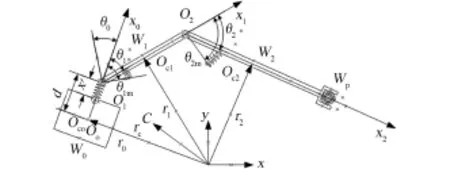
图2 具有弹性基座的柔性关节空间站机械臂Fig.2 Flexible joint manipulator of the space station with elastic base
图2为简化后的具有弹性基座的柔性关节空间站机械臂系统,它是平面两杆机构。为了简化运算,将导轨弹性简化为一个轻质弹簧,弹性位移为x′,并且作以下假设[23]:
1)弹簧的质量忽略不计;
2)弹簧只作伸缩运动;
3)弹簧的弹性系数k为一个常数。
建立惯性坐标系OXY及分体Wi(i=0,1,2)的连动坐标系OiXiYi,并假设系统沿(X,Y)平面作平面运动;此外,图中θ0为空间站载体姿态的实际转角,θim(i=1,2)各关节驱动电机的实际转角,θi(i=1,2)为连杆Wi的实际转角。
文中符号约定如下:m0、I0、l0分别为载体的质量、转动惯量及其质心到第1个关节铰中心的距离;mi、Ii、li分别为刚性机械臂Wi(i=1,2)的质量、转动惯量及其长度;mP、IP分别为末端刚性载荷WP的质量及转动惯量;由于载荷WP是由机械臂W2末端爪手抓持着,因此可将机械臂W2与载荷WP看成一联合体,其总质量和总转动惯量为m2P、I2P;Iai为柔性关节i(i=1,2)驱动电机的等效转动惯量,Wi(i=1,2)为各关节铰的扭转刚度;r0、r1分别为载体及连杆1质心的位置矢量,r2为连杆2与末端负载联合体质心的位置矢量,rC、rP分别为系统总质心及负载质心的位置矢量。各分体Wi(i=1,2)的转动角速度为vi,机械臂W2与载荷WP的联合体的转动角速度为vp=v2,关节Oi(i=1,2)处电机转子的自转角速度为vai。
若不考虑任何外力的作用,具有弹性基座的柔性关节空间站机械臂将满足系统动量及动量矩守恒的动力学约束关系。则由上述动力学约束关系及拉格朗日法,可解得载体位置、姿态均不受控的系统完全驱动形式的动力如式(1)~(3):
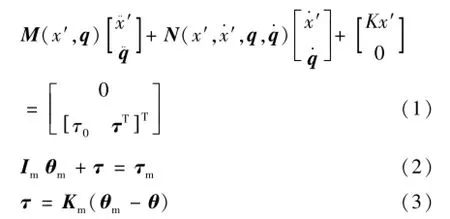
其中,q=[θ0θT]T、θ=[θ1θ2]T为机械臂各连杆转角列向量,θm=[θ1mθ2m]T为各关节驱动电机转角列向量;M(x′,q)∈ ℝ4×4和分别为机械臂连杆端的正定、对称惯性矩阵及包含科氏力、离心力的列向量;Im=diag(Im1,Im2)为驱动电机端的对角、正定惯量矩阵;Km=diag(Km1,Km2)为对角形式的柔性关节扭转刚度矩阵,K为空间站载体基座的弹性刚度;为各关节的线性扭转刚度;τ0为空间站载体的驱动力矩,τ=(τ1,τ2)∈ℝ2为由关节柔性所产生的连杆驱动力矩列向量,τm∈ℝ2为关节驱动电机实际产生的控制力矩列向量。
显然式(1)表征系统的载体柔性和刚性运动,对其进行矩阵分解得式(4):

式中,下标r,f分别与广义坐标x、q对应。因此表征系统刚性运动动力学方程为式(5):


可以看出,整个系统可视为由载体柔性刚性臂子系统(1)和电机转子子系统(2)组成,其子系统通过转子电机和机械臂的弹性力τ连接。本文的控制器设计目标是:存在参数不确定、外部扰动的情况下,合理的设计控制力矩τ0和τm,以实现载体姿态及关节角的协调运动控制,同时主动地抑制柔性关节与载体基座的弹性振动。
3 控制器设计及稳定性分析
依据级联控制法,分别为弹性基座刚性臂子系统和电机转子子系统设计相应的控制器,以实现控制目标。首先将载体系统驱动力矩τ0及关节铰系统所需的弹性力为中间控制变量,以实现载体姿态及关节角的轨迹跟踪控制且主动抑制载体基座的弹性振动。然后再设计关节电机输出力矩τm使电机转子子系统中反作用于关节的力矩τ跟踪计算所需的弹性力。显然,Δτ=τ-代表了关节的振动特性,通过将Δτ作为电机转子控制系统的反馈输入,能够快速控制关节实际输出力矩τ等于,以实现关节振动的主动抑制。
3.1 弹性基座刚性臂子系统的控制器设计
弹性基座刚性臂子系统与常规的柔性臂系统模型,动力学方程相似。为有效地实现载体姿态及关节角的协调运动控制及主动抑制载体基座的弹性振动,利用虚拟控制力生成能同时表征系统刚性运动和载体基座弹性振动的虚拟期望轨迹,再使针对表征系统刚性运动的刚性臂运动子系统而设计的鲁棒自适应滑模控制器跟踪该虚拟期望轨迹,以实现空间机械臂的载体姿态及关节角的轨迹跟踪同时主动抑制载体基座的弹性振动。
3.1.1 跟踪虚拟期望轨迹的鲁棒自适应滑模控制器设计
在实际应用中,系统的未建模动态、参数不确定及外部扰动等不可避免,为方便控制器的设计,将式(5)进行分离得到式(7)所示名义模型:
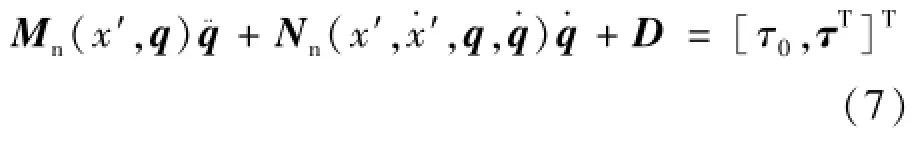
式中,矩阵Mn、Nn分别为Meq、Neq的估计值;为集中不确定项,d为外部扰动,假定不确定集中项存在上界,满足‖D‖≤ζ‖q‖,ζ>0。
设qd为具有弹性基座柔性关节空间站机械臂的期望轨迹,定义跟踪误差e=qd-q。定义虚拟期望轨迹qh,其与实际轨迹的误差定义为er=qh-q,与期望轨迹的误差定义为eh=qd-qh。而eh由式(8)二阶指令生成:
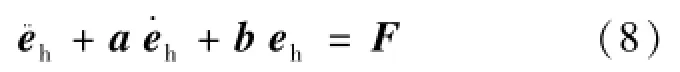
其中,a、b为对角正定矩阵;F为待设计的虚拟控制力,起着载体基座柔性振动抑制及保持系统刚性运动的作用。
滑模控制器是由等效控制项和切换控制项组成,等效控制项是用于维持系统在滑模面上运动,其性能由滑模面决定。切换控制项作用于滑模趋近运动阶段,迫使系统状态到达滑模面,性能是由滑模趋近律决定。滑模面设计如式(9):
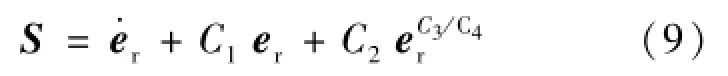
式中,参数C1>0,C2>0,C3和C4均为正奇数,且满足C3<C4<2C3。该滑模面在远离平衡点和接近平衡点都具有良好的收敛速度,且在有限时间内收敛到零。

为克服惯常使用的滑模切换控制项存在抖振现象与需要预知系统不确定的上界的缺陷,设计如式(11)所示鲁棒控制项代替的以往的滑模切换控制项:
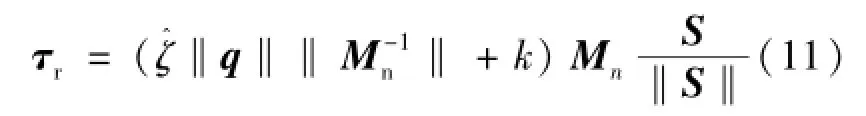
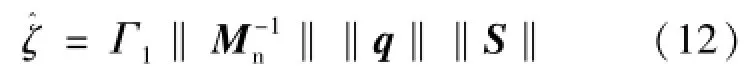
式中,Γ1>0为参数的学习率。
因此,对于弹性基座刚性臂子系统跟踪虚拟期望轨迹的控制器如式(13):
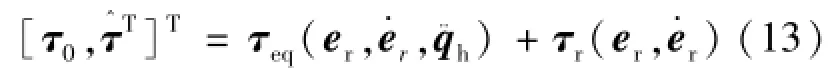
如果跟踪的是实际期望轨迹,其控制器形式为式(14):
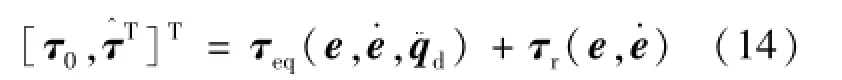
值得注意的是式(14)的控制器只能实现系统的刚性运动控制,不能主动抑制载体基座的弹性振动。如果控制器的设计忽略载体基座的弹性振动,则其控制器形式为式(15):
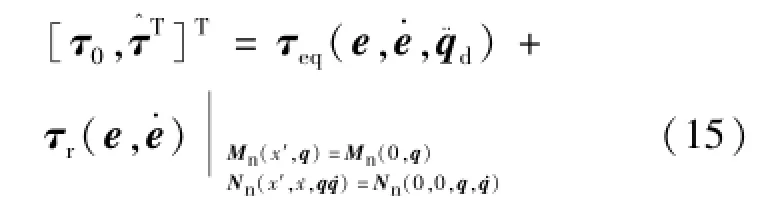
将控制器式(13)作用于子系统式(7)可得式(16):
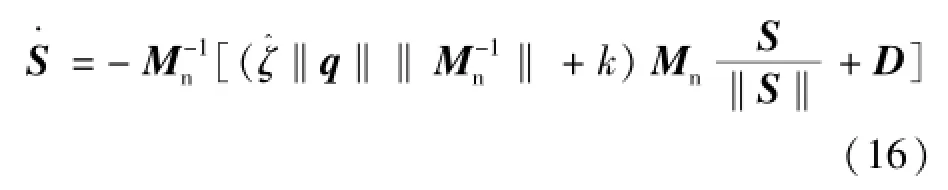
定义如式(17)所示正定Lyapunov函数:
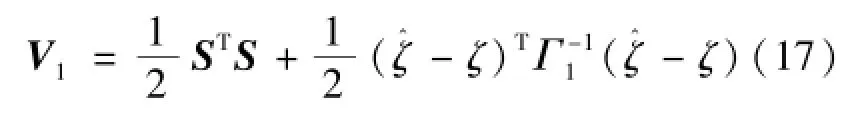
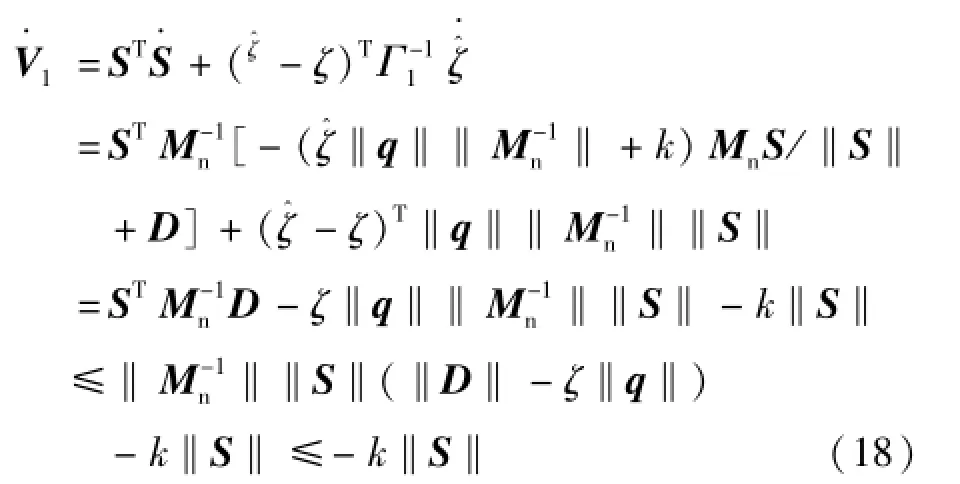
3.1.2 虚拟控制力的设计
上小节有个待设计的虚拟控制力F,该虚拟控制力作用于二阶指令生器,以生成虚拟期望轨迹qh。综合式(8)和(16),可得空间机器人系统的实际跟踪误差方程如式(18):
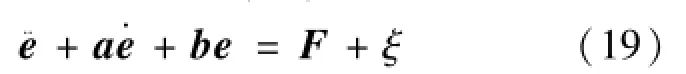
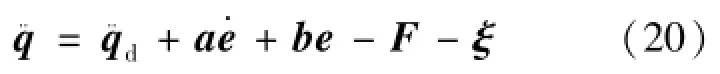
综合式(20)和式(6)可得空间站载体基座弹性振动方程如式(21):

由式(19)和式(21)可得包含空间站载体基座弹性振动和实际跟踪误差的状态方程如式(22):
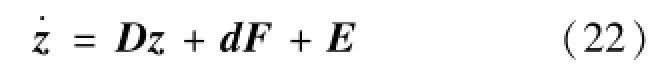
其中:
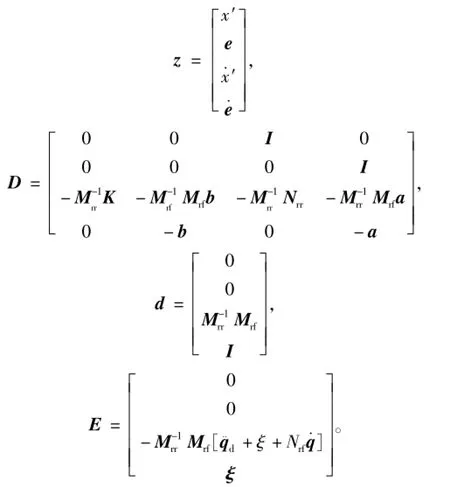
矩阵D和矩阵d为线性时变矩阵,矩阵E为非线性时变矩阵。将矩阵E视为干扰,使用线性二次型最优控制,并以减少状态向量z和控制能量F为优化目标如式(23):
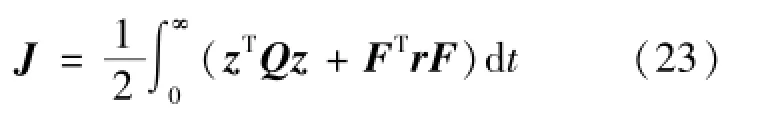
式中,Q∈ℝ8×8和r∈ℝ3×3为正定、半正定常值矩阵,则状态反馈最优控制为式(24):

其中,G为如式(25)所示Riccati方程的唯一解:
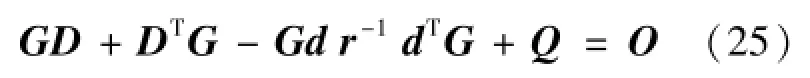
因此,闭环系统为式(26):

当E=O该状态反馈最优控制可保证闭环系统稳定,当E≠O稳定性分见参考文献[24]。至此完成了弹性基座刚性臂子系统的控制器的设计。
3.2 基于力矩反馈的关节柔性电机转子子系统的振动抑制设计
由于电机转子子系统中反作用于柔性关节的外力矩τ与计算输出的弹性力矩差代表了柔性关节的振动特性。为此,关节电机驱动力矩τm设计目标应是使τ快速跟踪,从而抑制柔性关节振动。设计如式(27)所示控制律:

其中,k2>O,k3>O均为对角正定阵。使用力矩传感器可省去电机转子的角速度和转角的测量反馈,减少传感器使用数量,提高控制系统可靠性。上式中切换函数可用双曲正弦函数代替。
目前针对柔性关节空间机械臂的控制方法主要为:基于奇异摄动法的控制方案设计[25]和基于柔性关节补偿的奇异摄动法控制方案设计[26],其快变子系统控制器的设计形式分别为如下:
奇异摄动法的快变子系统控制器如式(28):

基于柔性关节补偿的奇异摄动法快变子系统控制器如式(29):
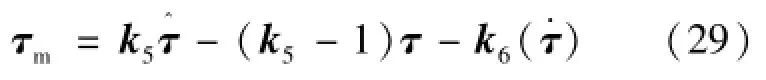
其中,k4、k5、k6均为设计参数。可以看出两种方案关于柔性关节振动的控制反馈信息均不足,限制了其只能应用于柔性关节刚度较大的情况。再者由于奇异摄动分解理论的束缚,这两种方案也很难运用于位置不控、姿态受控的这种电机转子数与柔性关节数不对等的数学模型。
将式(27)代入式(2)可得代表柔性关节弹性振动特性的误差方程,如式(30)所示:
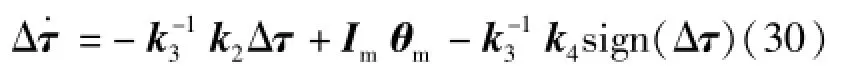
定义如式(31)所示正定Lyapunov函数:
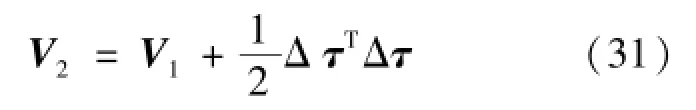
上式对时间求导可得式(32):
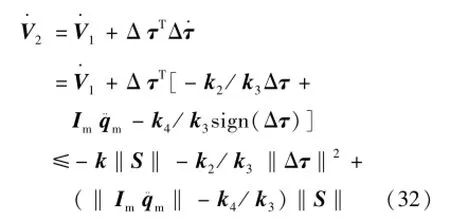
4 数值仿真算例及分析
以图3所示的具有弹性基座的柔性关节空间站机械臂为例,设载体基座的弹性刚度1200 N/m,柔性关节扭转刚度为Km1=Km2=15 N·m/rad,电机转子转动惯量为Im1=Im2=0.08 kg·m2。系统的其他真实参数及运动期望轨迹与初始值如表1所示。

表1 系统真实参数及运动期望轨迹与初始值Table 1 Real System parameters and the desired trajec⁃tory with initial value
并假设具有弹性基座的柔性关节空间站机械臂各关节角的期望运动轨迹分别为:(单位rad)
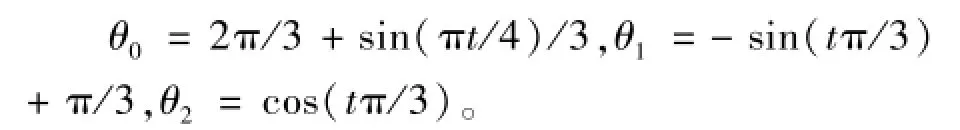
仿真时假定载体与刚性杆的转动惯量不可确知,其估计值分别为 25 kg·m2、2.5 kg·m2及1.5 kg·m2;载体基座弹性刚度的长度和柔性关节刚度的估计值分别为2000 N/m和10 N·m/rad。
控制参数选择如下:
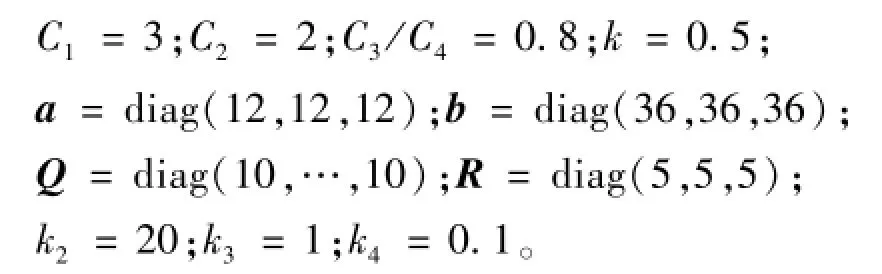
为验证文中设计的由弹性基座刚性臂子系统跟踪虚拟期望轨迹的控制器式(13)和抑制柔性关节振动控制器式(27)组合而成的级联控制器的有效性,本文采用了三组仿真对照实验。
第一组直接采用上述级联控制算法对系统进行数值仿真试验,仿真结果如图3~图8所示。
第二组为关闭虚拟控制力的情况下,由弹性基座刚性臂子系统跟踪实际轨迹的控制器式(14)和抑制柔性关节振动控制器式(27)组合而成的组合控制器作用于系统,其仿真结果如图9~图12所示。
第三组为忽略空间站载体基座弹性振动的控制器式(15)和抑制柔性关节振动控制器式(27)组合而成的组合控制器作用于系统,其空间站载体姿态及关节角的轨迹跟踪仿真如图13。

图3 载体姿态角θ0轨迹跟踪情况Fig.3 Trajectory tracking of the base's attitude θ0
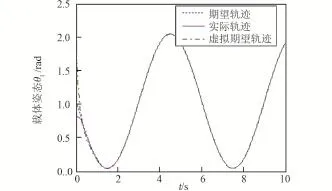
图4 载体姿态角θ1轨迹跟踪情况Fig.4 Trajectory tracking of the base's attitude θ1
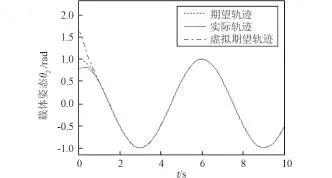
图5 载体姿态角θ2轨迹跟踪情况Fig.5 Trajectory tracking of the base's attitude θ2
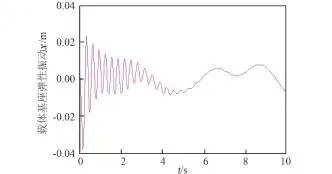
图6 载体基座弹性振动x(跟踪虚拟期望轨迹)Fig.6 Elastic vibration x of base(desired virtual trajectory)
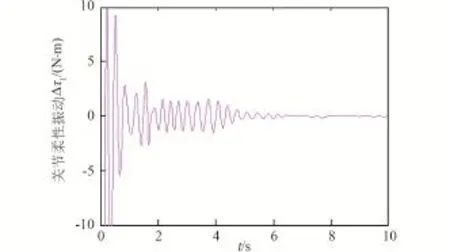
图7 柔性关节振动量Δτ1Fig.7 Vibration quantity Δτ1of the flexible joints

图8 柔性关节振动量Δτ2Fig.8 Vibration quantity Δτ2of the flexible joints

图9 载体姿态角θ0轨迹跟踪情况Fig.9 Trajectory tracking of the base's attitude θ0
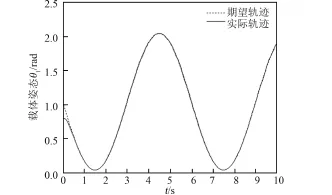
图10 载体姿态角θ1轨迹跟踪情况Fig.10 Trajectory tracking of the base's attitude θ1
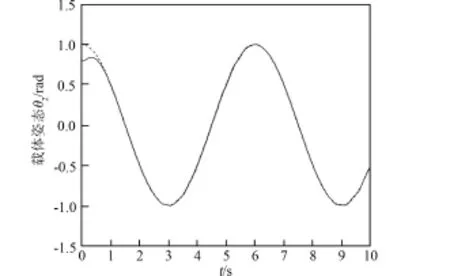
图11 载体姿态角θ2轨迹跟踪情况Fig.11 Trajectory tracking of the base's attitude θ2
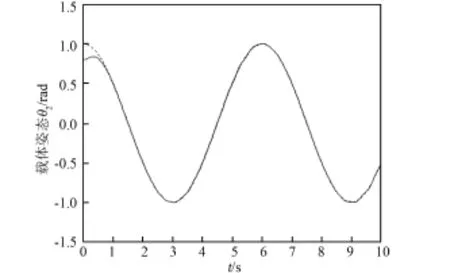
图12 载体基座弹性振动x(跟踪期望轨迹)Fig.12 Elastic vibration x of base(desired tracking traj⁃ectory)
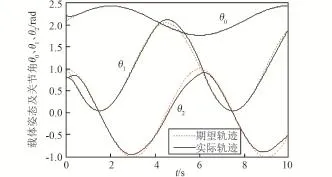
图13 载体姿态及关节角仿真图(忽略载体弹性)Fig.13 Trajectory tracking of the base attitude and the first and the second joint(ignore the base elasticity)
通过以上三组仿真对比实验可以看出:空间站载体基座的弹性振动会影响关节角的轨迹运动控制,而文中基于虚拟控制力而设计的控制力能够有效地抑制载体基座弹性振动,所提的级联控制方法能够有效地处理关节柔性,明显地抑制关节柔性振动。
5 结论
文中将级联系统法和虚拟力概念应用到弹性基座影响下空间站柔性关节机械臂控制器设计中,讨论了关节柔性和基座弹性同时存在情况下,参数未知空间站机械臂系统的动力学模拟过程、运动控制算法设计和双重柔性振动主动抑制。仿真结果表明:基于虚拟力概念的鲁棒自适应滑模控制器和级联控制方法在针对存在未知惯性参数的系统进行控制时,仅通过设计一个控制输入便可同时保证刚性轨迹跟踪并对空间站载体基座的弹性振动进行主动抑制,并且能够有效抑制柔性关节的振动,更适应于空间站柔性关节机械臂系统的实际应用。
(
)
[1]周建平.我国空间站工程总体构想[J].载人航天,2013,19(2):1⁃10.Zhou Jianping.Chinese space station project overall vision[J].Manned Spaceflight,2013,19(2):1⁃10.(in Chi⁃nese)
[2]于登云,孙京,马兴瑞.空间机械臂技术及发展建议[J].航天器工程,2007,16(4):1⁃8.Yu Dengyun,Sun Jing,Ma Xingrui.Suggestion on develop⁃ment of Chinese space manipulator technology[J].Spaceraft Engineering,2007,16(4):1⁃8.(in Chinese)
[3]Jarzbowska E,Pietrak K.Constrained mechanical systems modeling and control:A free⁃floating space manipulator case as a multi⁃constrained system[J].Robotics and Autonomous Systems,2014,62(10):1353⁃1360.
[4]Pisculli A,Felicetti L,Gasbarri P,et al.A reaction⁃null/Ja⁃cobian transpose control strategy with gravity gradient compen⁃sation for on⁃orbit space manipulators[J].Aerospace Science and Technology,2014,38:30⁃40.
[5]Leslie S,Benoit M,Pierre J,et al.Canada and the interna⁃tional space station program:overview and status since IAC 2008[C]//Proceedings of the 60th International Astronautical Congress.Daejeon:IAF,2009.3049⁃3058.
[6]Landzettel K,Preusch C,Albu⁃Schaffer A,et al.Robotic on⁃orbit serving⁃DLR's experience and perspective[C]//Pro⁃ceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway,New Jersey,U⁃nited States:IEEE,2006.4587⁃4594.
[7]李俊峰,王照林.带空间机械臂的充液航天器姿态动力学研究[J].宇航学报,1999,20(2):81⁃86.Li Junfeng,Wang Zhaolin.Study on attitude dynamics of a liquid⁃filled spacecraft with manipulators[J].Jouranl of As⁃tronautics,1999,20(2):81⁃86.(in Chinese)
[8]张大伟,梁常春,危清清.机械臂辅助舱段转位轨迹跟踪控制与精度分析[J].载人航天,2014,20(2):103⁃109.Zhang Dawei,Liang Changchun,Wei Qingqing.Trajectory tracking control and accuracy analysis of space robotic arm as⁃sisted cabin redocking[J].Manned Spaceflight,2014,20(2):104⁃109.(in Chinese)
[9]梁捷,陈力.具有时延的漂浮基空间机器人基于泰勒级数预测、逼近的改进非线性反馈控制[J].航空学报,2012,33(1):163⁃169.Liang Jie,Chen Li.Improved nonlinear feedback control for free⁃floating space⁃based robot with time⁃delay based on pre⁃dictive and approximation of taylor series[J].Acta Aeronouti⁃caet Astronautica Sinica,2012,33(1):163⁃169.(in Chi⁃nese)
[10]梁捷,陈力.漂浮基空间机器人捕获卫星过程动力学模拟及捕获后混合体运动RBF神经网络控制[J].航空学报,2013,34(4):970⁃978.Liang Jie,Chen Li.Dynamics modeling for free⁃floating space⁃based robot during capture satellite and radial basis function neural network control for compound body stable movement[J].Acta Aeronouticaet Astronautica Sinica,2013,34(4):970⁃978.(in Chinese)
[11]戈新生,陈立群,吕杰.空间机械臂非完整运动规划的遗传算法研究[J].宇航学报,2005,26(3):262⁃266.Ge XinSheng,Chen LiQun,Lv Jie.Nonholonomic motion planning of a space manipulator system using genetic algorithm[J].Journal of Asronautics,2005,26(3):262⁃266.(in Chinese)
[12]丁希仑,俞玉树.一种多旋翼多功能空中机器人及其腿式壁面行走运动规划[J].航空学报,2010,31(10):2075⁃2086.Ding Xilun,Yu Yushu.A multi⁃propeller and multi⁃function aero⁃robot and Its motion planning of leg⁃wall⁃climbing[J].Acta Aeronouticaet Astronautica Sinica,2010.31(10):2075⁃2086.(in Chinese)
[13]李青,王天舒.高频激励下旋转柔性臂逆动力学模态自适应方法研究[J].空间科学学报,2008,28(4):345⁃349.Li Qing,Wang Tianshu.Adaptive mode method in inverse dy⁃namics of a rotating flexible manipulator with high⁃frequency excitation[J].Chinese Journal of Space Science,2008,28(4):345⁃349.(in Chinese)
[14]阎绍泽,黄铁球,吴德隆,等.空间飞行器柔性附件动力学建模方法研究[J].导弹与航天运载技术,1999(2):31⁃39.Yan Shaoze,Huang Tieqiu,Wu Delong,et al.Study on dy⁃namics modeling of a flexible appendage of spacecraft[J].Missles and Space Vehicle,1999(2):31⁃39.(in Chinese)
[15]章定国.多杆空间柔性机器人递推Lagrange动力学建模和仿真[J].应用数学和力学,2009,30(10):1202⁃1212.Zhang Dingguo.Recursive lagrangian dynamic modeling and simulation of multi⁃link spatial flexible manipulator arms[J].Applied Mathematics and Mechanics,2009,30(10):1202⁃1212.(in Chinese)
[16]吴立成,孙富春,孙增圻,等.柔性空间机器人振动抑制轨迹规划算法[J].机器人,2003,25(3):250⁃254.Wu Licheng,Sun Fuchun,Sun zengqi,et al.Optimal trajec⁃ tory planning of flexible space robot for vibration reducing[J].Robot,2003,25(3):250⁃254.(in Chinese)
[17]洪在地,贠超,陈力.柔性臂漂浮基空间机器人建模与轨迹跟踪控制[J].机器人,2007,29(1):92⁃96.Hong Zaidi,Yun Chao,Chen Li.Modeling and trajectory tracking control of a free⁃floating space robot with flexible ma⁃nipulators[J].Robot,2007,29(1):92⁃96.(in Chinese)
[18]梁捷,陈力,梁频.空间机械臂刚柔耦合动力学模拟及小波基模糊神经网络控制[J].载人航天,2015,21(3):286⁃294.Liang Jie,Chen Li,Liang Pin.The rigid⁃flexible coupling dynamics simulation and wavelet based fuzzy neural network control for space manipulator[J].Manned Spaceflight,2015,21(3):286⁃294.(in Chinese)
[19]Lindsay Evans.Canadian space robotics on board the interna⁃tional space station[C]//2005 CCToMM Symposium on Mechanisms,Machines,and Mechatronics.Canadian Space Agency,Montreal,Canada.May 26⁃27,2005.
[20]Yang B J,Calise A J,Craig J I.Adaptive output feedback control of a flexible base manipulator[J].Journal of Guid⁃ance,Control and Dynamics,2007,30(4):1068⁃1080.
[21]Stieber M F,Trudel C P,Hunter D G.Robotic systems for the international space station[C]//Proceedings of the 1997 IEEE International Conference on Robotics and Automation Albuquerque,IEEE,1997.3068⁃3073.
[22]Evans L.Canadian space robotics on board the international space station[C]//2005 CCToMM Symposium on Mecha⁃nisms,Machines,and Mechatronics.Canadian Space Agen⁃cy,Montreal,Canada.2005:26⁃27.
[23]Spong M W.Modeling and control of elastic joint robots[J].Journal of Dynamics Systems,Measurement and Control,1987,109(4):310⁃319.
[24]Patel R V,Toda M,Sridhar B.Robustness of linear quadrat⁃ic state feedback designs in the presence of system uncertainy[J].IEEE Tranactions on Automatic Control,1977,22(6):945⁃949.
[25]梁捷,陈力.关节柔性的漂浮基空间机器人基于奇异摄动法的轨迹跟踪非奇异模糊Terminal滑模控制及柔性振动抑制[J].振动与冲击,2013,32(23):6⁃12.Liang Jie,Chen Li.Nonsingular fuzzy terminal sliding mode control and elastic vibration suppressing of a free⁃floating space robot with flexible joints based on trajectory tracking of the singular perturbation method[J].Journal of Vibration and Shock,2013,32(23):6⁃12.(in Chinese)
[26]梁捷,陈力.用于空间站和航天飞机的漂浮基柔性铰空间机器人的径向基函数神经网络自适应控制算法[C]//第三届载人航天学术大会.四川,成都,2014,11.Liang Jie,Chen Li.Radial basis function neural network a⁃daptive control algorithm of flexible⁃joint space robot that used in space shuttle and space station[C]//The third manned spaceflight academic conference.Sichuan,Chendu,2014,11.
Robust Adaptive Sliding Mode Control and Active Dual Vibration Suppression in Flexible Joint Manipulator of Space Station with Elastic Foundation
LIANG Jie1,3,CHEN Li2,LIANG Wulin3,QIN Kaiyu1
(1.School of Astronautics&Aeronautic,University of Electronic Science and Technology of China,Chengdu 611731,China;2.Department of Mechanical Engineering and Automation,Fuzhou University,Fuzhou 350108,China;3.China Aerodynamics Research and Development Center,Mianyang 621000,China)
The trajectory tracking control and the vibration suppression of the flexible joint manipu⁃lator in the space station with elastic base were discussed in this paper.The Lagrangian method and the momentum conservation were adopted in building the dynamic equations.The system could be viewed as a cascade control system consisting of the rigid subsystem of the elastic base and the actua⁃tor dynamics system of the flexible joint.To actively damp out the vibration in the rigid subsystem of the elastic base,the conception of virtual force was used to design the hybrid desired trajectory re⁃flecting both the flexible mode and the rigid motion.The original control scheme was modified and a robust adaptive sliding mode control based on the virtual force conception was proposed.By using the concept of virtual force,the rigid trajectory tracking and active suppression of the flexible vibra⁃tion in the elastic base were realized just with one control input which was more suitable for the prac⁃tical application of the flexible joint manipulator in the space station.At the same time,the vibration of the flexible joint could be effectively suppressed with the cascade control method even in case of unknown system parameters.The theoretical analysis and simulation results verified the feasibility of the proposed control schemes.
space station;flexible joint manipulator;elastic base;dynamic mode;robust adaptive sliding mode control;active suppression of flexible vibration
V476.1
A
1674⁃5825(2016)06⁃0788⁃09
2016⁃05⁃30;
2016⁃11⁃14
国家高技术研究发展计划(863计划)基金项目(2015AA7055041);国家自然科学基金(11372073);四川省科技厅应用基础项目(2016Y0210)
梁捷(1971-),男,博士后,研究方向为飞行器动力学与控制。E⁃mail:myamoy81@163.com

