探月返回跳跃式再入标称轨迹制导律
杜 昕,刘会龙,黄悦琛
(1.中国空气动力研究与发展中心高速空气动力所,绵阳621000;2.国防科技大学航天科学与工程学院,长沙410072)
探月返回跳跃式再入标称轨迹制导律
杜 昕1,刘会龙1,黄悦琛2
(1.中国空气动力研究与发展中心高速空气动力所,绵阳621000;2.国防科技大学航天科学与工程学院,长沙410072)
针对目前大多数跳跃式再入制导方案在初次再入段采用数值预测⁃校正算法存在的计算量较大、在线应用困难的问题,提出了一种新的跳跃式再入标称轨迹制导方案。整条标称轨迹通过离线轨迹规划算法得到。在初次再入段,采用非线性预测控制算法来跟踪阻力加速度⁃能量剖面,将预测跟踪误差表示为依赖于控制量的截断泰勒展开式,然后寻找使得特定目标函数最小的控制量。进入二次再入段,采用类似于阿波罗末段制导的线性反馈跟踪方式,PID控制器系数通过插值得到。最后,在考虑各种误差的情况下进行了500次蒙特卡洛仿真,仿真结果表明制导律的精度较高,鲁棒性较好。
探月返回;跳跃式再入;标称轨迹制导;非线性预测控制;线性反馈控制
1 引言
再入制导一般可分为纵向制导和横向制导。横向制导一般通过倾侧角反转来实现,纵向制导则方法多样,一般分为标称轨迹制导和预测制导[1]。针对跳跃式再入情况,Draper实验室最先将数值预测⁃校正算法引入,形成了跳跃式再入的数值预测制导方案PredGuid[2]。此后,对于跳跃式再入数值预测制导的研究开始增多,如NASA的 NSEG[3]以及 Ping Lu、Christopher的研究工作[4⁃5]等。Kluever研究了跳跃式再入的解析预测校正制导[6]。
标称轨迹制导方法多样,可以直接跟踪返回舱的状态量[7⁃9],也可以跟踪阻力加速度剖面[10]。阻力加速度制导能有效降低制导性能对气动模型和大气模型的依赖性[11]。Apollo再入制导奠定了阻力加速度制导方法的基础,航天飞机的再入制导使阻力加速度制导方法得到进一步发展[10]。阻力加速度制导可以跟踪阻力加速度⁃速度剖面,也可以跟踪阻力加速度⁃能量剖面[12⁃13]。
对阻力加速度制导而言,最为关键的问题是阻力加速度剖面的跟踪算法。在Apollo和航天飞机的再入制导里,阻力加速度剖面的跟踪通过PID控制实现,它忽略了阻力加速度偏差动力学中的非线性项[14];Mease通过研究航天飞机的非线性动力学特性,利用反馈线性化理论跟踪阻力加速度剖面,发展出一种改进阻力加速度制导算法EAGLE[15];但是,当存在模型偏差或出现控制饱和情况,或者这两种情况同时发生时,线性反馈跟踪方式无法实现误差的渐进稳定。通过滑模控制器来改进线性反馈控制方式可以较好地解决模型偏差的问题[16]。Ping Lu引入模型预测控制的思想来跟踪阻力加速度剖面,发展出连续时间非线性预测控制(Continuous⁃Time Nonlinear Predic⁃tive Control,CTNPC)方法,预测的跟踪误差用控制量的有限泰勒展开式来表示,通过求解非线性优化问题来得到控制量,使得某一和预测偏差相关的目标函数取得极值[17⁃18]。Benito沿着 Ping Lu的方向,采用了不同的目标函数来得到不同形式的控制率,并应用于火星的进入制导[19]。实际上,早在20世纪70年代,工业控制过程就用到了模型预测控制[20](Model Predictive Control, MPC),更多关于 MPC的细节可以参考文献[21]。MPC是要预测一段时间内(若干个控制周期内)的系统输出,控制量的选取是要使得预测值与标称值之间的偏差最小。这个过程在MPC中称为滚动优化,通常采用数值优化算法求解。而众所周知,数值优化算法求解速度较慢,这就限制了MPC的在线应用。而CTNPC则选取了较短的预测时域增量,并且采用截断的泰勒展开,从而对滚动优化问题进行了简化,避免了大量的数值计算,可以推导出一定精度下的近似解析最优解。
本文引入CTNPC来跟踪跳跃式再入初次再入段的阻力加速度⁃能量剖面,采用线性反馈控制来跟踪二次再入段参考轨迹,由此得到一种新的跳跃式再入标称轨迹制导方案。并在考虑各种误差的情况下通过500次蒙特卡洛仿真,验证该制导方案的有效性,以及相对PredGuid、NSEG等在初次再入段采用数值预测⁃校正算法的制导方案在制导精度和计算时间上的表现。
2 标称轨迹制导的数学模型
2.1 三自由度再入方程
考虑地球为旋转圆球的三自由度再入动力学方程如式(1)~(6)[4]:

其中,r为地心距,θ为经度,φ为纬度,V为返回舱速度,γ为飞行路径角,ψ为速度方位角(正北方向为零,顺时针旋转为正),σ为滚转角,ω为地球自转角速度,g为重力加速度,L和D分别为升力加速度和阻力加速度,定义如式(7)~(8):
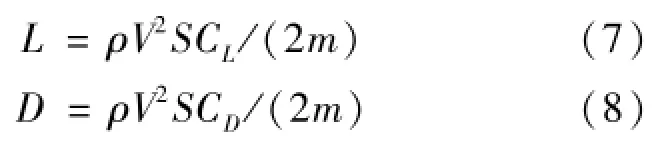
其中,ρ为大气密度,m为返回舱质量,S为返回舱参考迎风面积。
2.2 阻力加速度动力学模型
假设阻力系数CD为常数,大气密度模型为指数模型,并忽略地球自转,对阻力加速度D的表达式求导数可得式(9):

求导过程中做了如下近似:D+gsinγ≈D以及cosγ≈1。
对上式进一步求导得式(10):
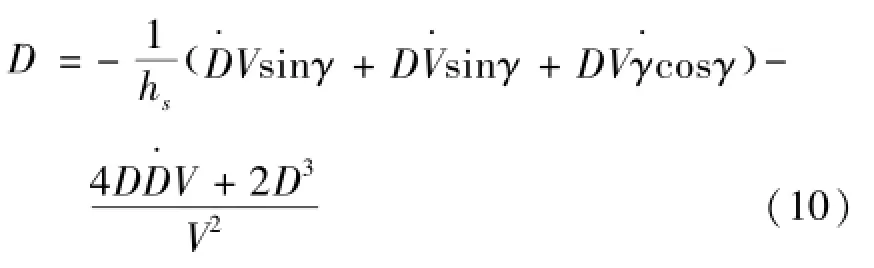
展开后得式(11):
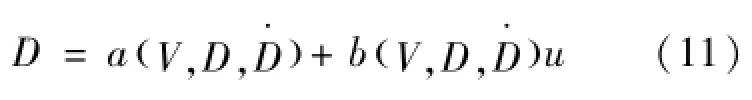
式中:
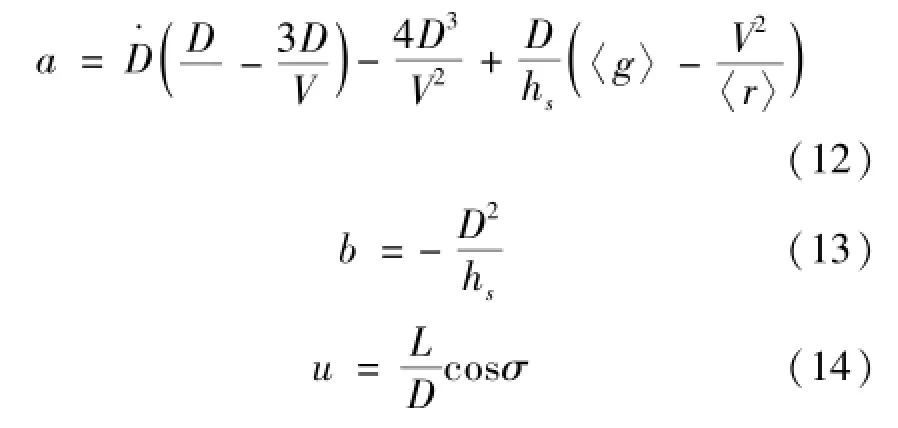
2.3 制导律总体设计
如果在跳跃式再入的全程都跟踪事先设计好的这一条标称轨迹,那么到达开伞条件时的纵程累积偏差是比较大的,轨迹的可调节性较差。A⁃pollo再入末段所采用的线性反馈跟踪制导已经被证明在末段具有较高的精度,且能适应不同的二次再入条件,轨迹具有较大的可调节性[3]。因此,在设计的时候,标称轨迹是整段一起设计,而在制导律实现的时候,轨迹初次再入段采用非线性跟踪算法跟踪阻力加速度剖面,当轨迹进入二次再入段则采用Apollo末段的线性反馈跟踪方式。整个过程的制导律设计如图1所示。
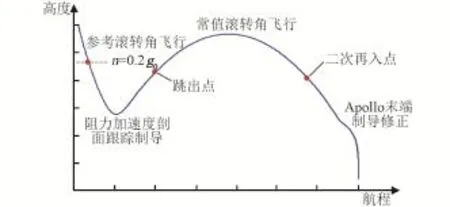
图1 制导律总体设计Fig.1 Framework of the guidance strategy
在初始滚转段(即再入点到过载首次达到0.2g0),气动控制能力十分有限,滚转角取值对轨迹的影响很小,因此在这一段中不进行制导解算,直接采用参考轨迹的滚转角进行飞行,同时这也可以避免线性反馈跟踪出现控制饱和的情况。
2.4 阻力加速度跟踪制导原理
轨迹跟踪采用阻力加速度跟踪方式,跟踪参考轨迹的阻力加速度⁃能力剖面。定义能量E为式(15):

其中,μ为地球引力常数。为方便比较不同轨迹之间的跟踪特性,将能量进行归一化处理,定义归一化能量如式(16):

其中,Ei是轨迹初始时刻的能量,Ef是轨迹终止时刻的能量。这样一来,就代表轨迹初始点,就代表轨迹终止点。
定义航程如式(17):

对能量E的表达式求导可得式(18):

航程可表示为式(19):
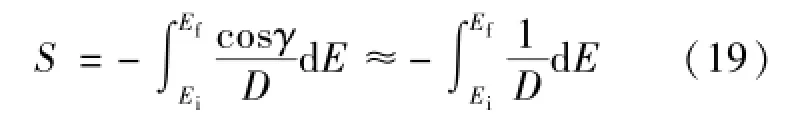
从式(19)可以看出,准确地跟踪D-E剖面,就能准确地跟踪航程S。
3 分段跟踪算法设计
3.1 非线性预测控制器
本文采用的非线性预测控制器是基于Ping Lu的连续时间非线性预测控制(Continuous⁃Time Nonlinear Predictive Control,CTNPC)算法[16]。给定如式(20)~(21)所示的非线性系统:

其中,x∈ℝn是状态量,u∈ℝm是输入控制量,y∈ℝl是输出量。非线性控制器的目的是跟踪一个参考输出量qt(),使式(22)所示目标函数达到最小。
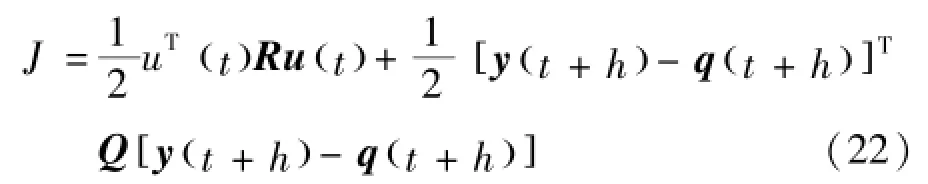
其中,Q∈ℝl×l是正定矩阵,R∈ℝm×m是半正定矩阵。设ηi是yi的相对次数,并且时间步长h>0是小量,系统输出近似为式(23):
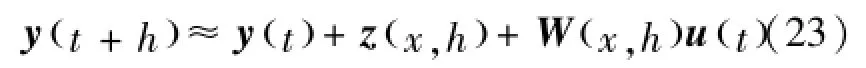
其中z(x,h)满足式(24):
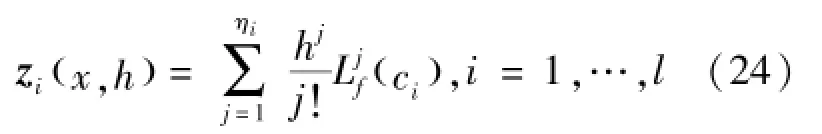
其中,L表示李导数,详细定义可参考文献[14]。
W(x,h)∈ℝl×m的第i行为式(25)所示:
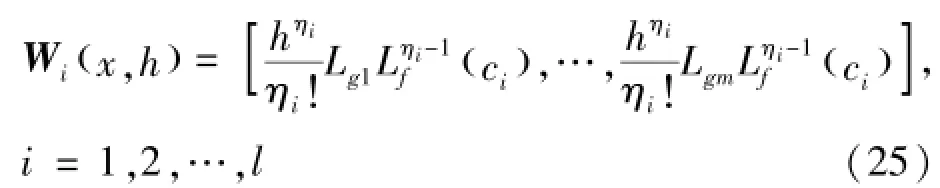
而q(t+h)可以近似表示为式(26):
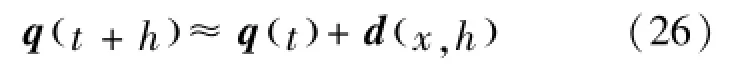
其中d(x,h)满足式(27):
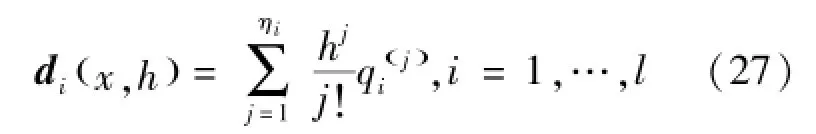
令∂J/∂u=0,得到式(28):

其中,e(t)=y(t)-q(t)为跟踪误差。
3.2 初次再入段轨迹跟踪
对于再入问题,有n=6,m=1(只有滚转角一个输入控制量)。跟踪时,考虑跟踪阻力加速度D和阻力加速度变化率两个量,因此有l=2,η1=2,η2=1。跟踪误差定义为式(29)~(30):


其中,下标“r”代表参考轨迹。
t+h时刻的预测误差可以近似表示为式(31)~(32):

设Q∈ℝ2×2是对角线矩阵,对角线元素为α1≥0、α2≥0,并且R=0,目标函数变为式(33):
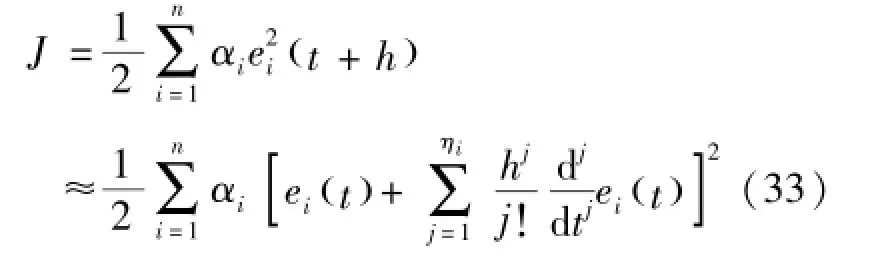
目标函数对控制量的偏导为式(34):

由式(11)、(29)、(30)可以得到式(35)~(36):

因此有式(37)~(38):
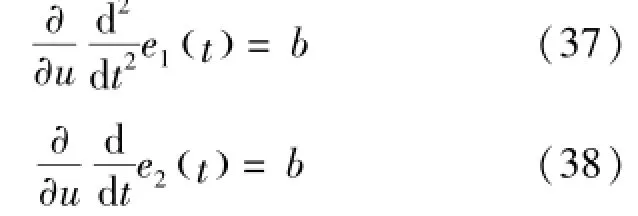
将式(37)~(38)代入式(34),得到式(39):
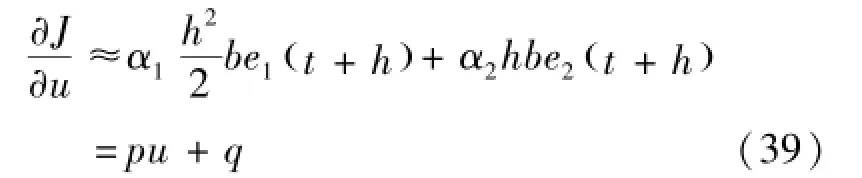
其中:
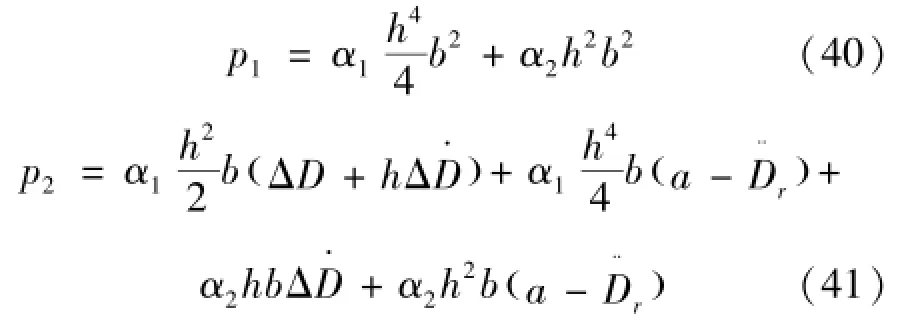

3.3 二次再入段轨迹跟踪
二次再入段采用Apollo末段所采用的线性反馈跟踪方式,它的标称轨迹是离线生成,采用线性PID控制[17]。PID控制器系数为航程对阻力加速度的导数f1、航程对高度变化率的导数f2以及航程对升阻比的导数f3,这些系数都是离线生成并储存在星载计算机上。f1、f2以及f3的定义如式(44)所示。

其中,H为飞行高度。
而航程预测通过式(45)实现,其中参考值都是通过对标称轨道进行插值得到(速度插值)。

然后,求得操纵升阻比如式(46):
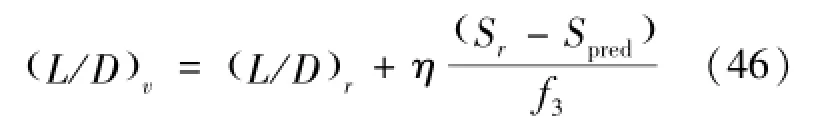
其中,η为经验系数,其主要作用是当轨迹偏离参考轨迹较大时,用来修正线性化带来的不准确性。
最后,得到指令滚转角如式(47):
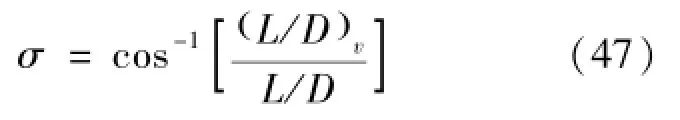
4 仿真结果与分析
4.1 条件设置
返回舱参数取 Apollo返回舱参数[2],质量5500 kg,大底截面直径3.9 m,驻点曲率半径2.5 m,升力系数0.38773,阻力系数1.2891。
再入初始条件为:再入高度120 km,再入点经度0°,再入点纬度0°,再入速度10.66 km/s,再入角-6.2°,再入方位角45°。
假定任务航程为6000 km,由此计算出开伞点经度44.29°,开伞点纬度34.92°,标称轨迹通过轨迹优化方法得到。
误差源的类型及其量级参考 CEV的标准[20],如表1所示。
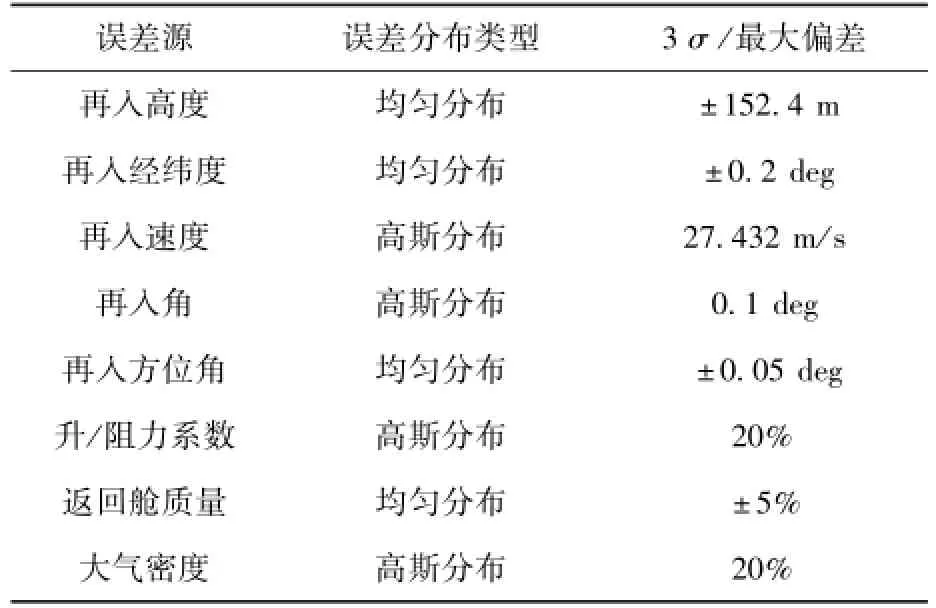
表1 再入误差源类型及其级别Table 1 Dispersions in the entry interface state and oth⁃er parameters
真实的大气密度偏差总体上具有“低空小,高空大”的规律,目前国际上公认比较准确的大气密度偏差模型是美国的Earth Global Reference Atmosphere Model(GRAM)模型[21]。由于无法获得GRAM的数据,本文采用如式(48)所示的正弦形式解析模型来模拟大气偏差模型[22]。
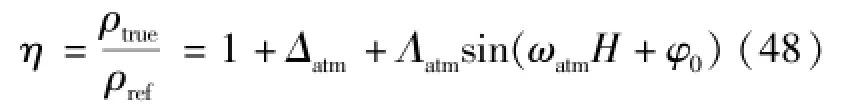
其中,ρtrue为真实大气密度,ρref为美国1976标准大气模型计算得到的标称大气密度,Δatm、Λatm为在±0.15范围内均匀分布的随机数,ωatm>0以及φ0为常值系数。该模型500次仿真的结果如图2所示。

图2 解析形式的大气密度误差模型Fig.2 Density dispersions as a function of altitude
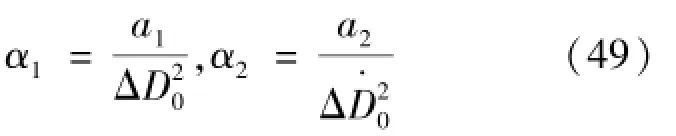
其中,a1、a2为无量纲参数,ΔD0、为相应的跟踪误差门限值。本文中,取a1=1.6,ΔD0=4 m/s2,a2=0.5,Δ0=0.5 m/s3。
4.2 结果分析与讨论
考虑所有的偏差(包括初始状态偏差、返回舱质量偏差、大气密度偏差以及升阻力系数偏差),进行500次蒙特卡洛弹道仿真,初次再入段轨迹跟踪结果如图3~图6所示,其中红色线表示参考轨迹曲线。
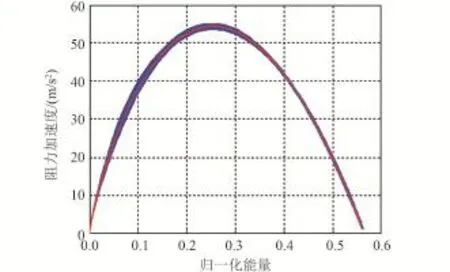
图3 阻力加速度跟踪曲线Fig.3 Reference and actual drag profiles
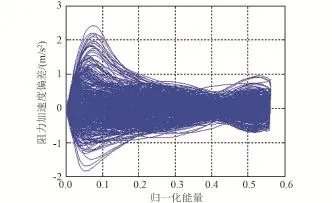
图4 阻力加速度跟踪误差Fig.4 Drag tracking errors

图5 阻力加速度变化率跟踪曲线Fig.5 Reference and actual drag rate profiles
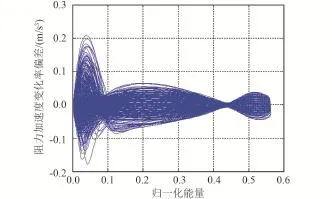
图6 阻力加速度变化率跟踪偏差Fig.6 Drag rate tracking error
从图3可以看到,在考虑所有偏差的情况下,阻力加速度的跟踪精度总体较高,且跟踪偏差呈现出先增大后减小的变化规律,这一点从图4中可以清晰地看到,一开始阻力加速度偏差较小,随后逐渐增大,并且在附近达到峰值,然后再一次减小,并最终振荡保持在一个较小的范围内(±1 m/s2)。
从图5可以看到,在考虑所有偏差的情况下,阻力加速度变化率的跟踪精度总体较高。从图6中可以清晰地看到,一开始阻力加速度变化率的跟踪偏差较小,随后逐渐增大,并且在附近达到峰值,然后再一次减小,并最终振荡保持在一个较小的范围内(±0.1 m/s3)。
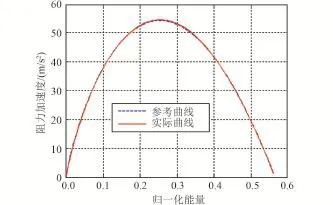
图7 阻力加速度跟踪偏差(CTNPC)Fig.7 Drag tracking error(CTNPC)
将本文算法与线性反馈算法进行对比。由于是跟踪初次再入段轨迹,线性反馈算法采用文献[26]的方法。线性反馈方式主要是在大误差情况下表现较差。因此,暂不考虑其他误差,仅将初始经度误差设定为一个较大的值 -0.1483°,两种跟踪方式的对比结果如图7~10所示。
可以看到,在初始误差较大时,小扰动假设已经不再适用,从而导致线性反馈方式的跟踪精度较差。而非线性预测方式的跟踪精度仍然较高,因此它的鲁棒性更好。
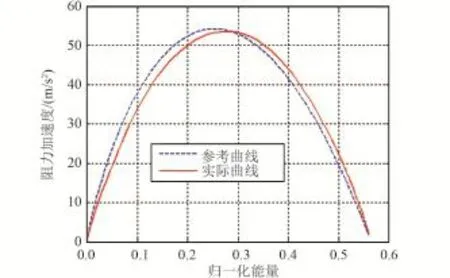
图8 阻力加速度跟踪偏差(线性反馈)Fig.8 Drag tracking error(FBL)

图9 阻力加速度变化率跟踪偏差(CTNPC)Fig.9 Drag rate tracking error(CTNPC)

图10 阻力加速度变化率跟踪偏差(线性反馈)Fig.10 Drag rate tracking error(FBL)
整个跳跃式再入轨迹的蒙特卡洛仿真如图11~13所示。从图11可以看到,轨迹的最大跳跃高度绝大部分超过了100 km。从图12可以看到,由于轨迹的跳跃,过载出现了两次峰值,大多数情况下初次再入段的过载峰值大于二次再入段的过载峰值,少部分情况下二次再入段的过载峰值要大于初次再入段过载峰值,但均没有超出过载约束(7g0)。而且过载包络曲线在初次再入段较为“集中”,在二次再入段较为“发散”,这是因为初次再入段制导律是跟踪阻力加速度。
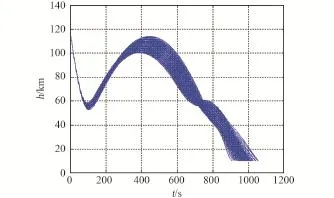
图11 飞行高度包络曲线Fig.11 Time history of altitude for the dispersed traj⁃ectories
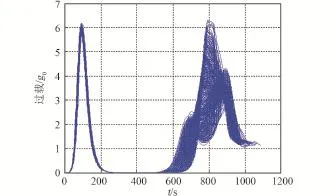
图12 过载包络曲线Fig.12 Time history of load for the dispersed trajec⁃tories
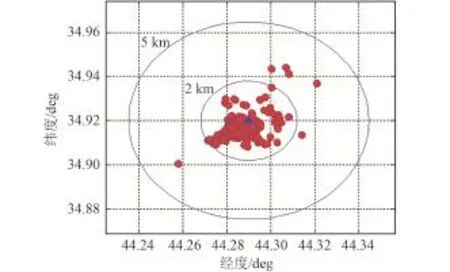
图13 落点散布图Fig.13 Final positions of the dispersed trajectories
从图13可以看到,最终的制导精度较高,98.8%的落点都分布在2 km的偏差带内,1.2%的落点分布在2 km~5 km的偏差带内。
初次再入段采用文献[24]中数值预测⁃校正算法,二次再入段同样采用 Apollo末段跟踪算法,在同样的条件下进行500次仿真,结果如图14所示。可以看到,其制导精度与图13中的制导精度相当。但与本文的CTNPC算法相比,预测校正算法的计算时间增加了几十倍。
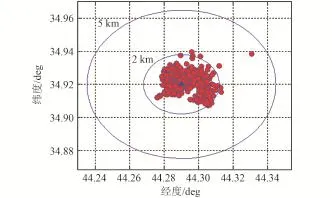
图14 落点散布图(预测校正)Fig.14 Final positions of the dispersed trajectories(predictor⁃corrector)
5 结论
本文提出了一种新的标称轨迹制导方案,并利用蒙特卡洛仿真对制导律进行了测试,结果表明:
1)初次再入段采用的非线性预测控制跟踪算法精度较高,能准确跟踪阻力加速度剖面,无论是阻力加速度的跟踪误差还是阻力加速度变化率的跟踪误差都振荡收敛至一个较小的范围。
2)二次再入段航程较短,所采用的线性反馈跟踪算法的精度足够高,因此使得整个制导律的制导精度较高。蒙特卡洛仿真结果也表明制导律还具有较高的鲁棒性。
3)由于初次再入段制导律是跟踪阻力加速度,因此初次再入段的过载曲线较为集中。在所有的500次轨迹中,过载均没有超出约束,说明制导律实际可行。
(
)
[1]Wingrove R C.Survey of atmosphere re⁃entry guidance and control methods[J].AIAA Journal,1963,1(9):2019⁃2029.
[2]Bairstow S H.Reentry Guidance with Extended Range Capa⁃bility for Low L/D Spacecraft[D].Massachusetts:Massachu⁃setts Institute of Technology,2006.
[3]Tigges M,Crull T,Rea J,et al.Numerical skip⁃entry guid⁃ance[C]∥Proceedings of the 29th Annual AAS Guidance and Control Conference.San Diego,California,AAS:2006.
[4]Lu P.Entry guidance:a unified method[J].Journal of Guid⁃ance,Control,and Dynamics,2014,37(3):713⁃727.
[5]Brunner C W.Skip Entry Trajectory Planning and Guidance[D].Iowa:Iowa State University,2008.
[6]Kluever C A.Entry guidance using analytical atmospheric skip trajectories[J].Journal of Guidance,Control,and Dy⁃namics,2008,31(5):1531⁃1534.
[7]Roenneke A J,Cornwell P J.Trajectory control for a low⁃lift reentry profile[J].Journal of Guidance,Control,and Dy⁃namics,1993,16(5):927⁃933.
[8]Lu P.Nonlinear trajectory tracking guidance with application to a launch vehicle[J].Journal of Guidance,Control,and Dynamics,1996,19(1):99⁃106.
[9]雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙:国防科技大学,2008.Yong Enmi.Study on Trajectory Optimization and Guidance Approach for Hypersonic Glide⁃reentry Vehicle[D].Chang⁃sha:National University of?Defense Technology,2008.(in Chinese)
[10]陈刚,董龙雷,闫桂荣,等.航天器再入制导方法研究现状与发展评述[J].飞行力学,2008,26(1):1⁃4.Chen Gang,Dong Longlei,Yan Guirong,et al.Recent status and development review of spacecraft reentry guidance meth⁃ods[J].Flight Dynamics,2008,26(1):1⁃4.(in Chinese)
[11]Eduardo G L.Analytic development of a reference trajectory for skip entry[J].Journal of Guidance,Control and Dynam⁃ics,2011,34(1):311⁃317.
[12]Harpold J C,Graves C A.Shuttle entry guidance[J].The Journal of the Astronautical Sciences,1979,27(3):239⁃268.
[13]Roenneke A J,Markl A.Re⁃entry control of a drag⁃vs⁃energy profile[J].Journal of Guidance,Control and Dynamics,1994,17(5):916⁃920.
[14]Benito J.Advances in Spacecraft Atmospheric Entry Guidance[D].Irvine:University of California,2010.
[15]Saraf A,Leavitt J A,Chen D T,et al.Design and evaluation of an acceleration guidance algorithm for entry[J].Journal of Spacecraft and Rockets,2004,41(6):986⁃996.
[16]Talole S E,Benito J,Mease K D.Sliding mode observer for drag tracking in entry guidance[C]∥Proceedings of the AIAA Guidance,Navigation and Control Conference.Wil⁃liamsburg,Virginia,AIAA:2007.
[17]Lu P.Nonlinear predictive controllers for continuous systems[J].Journal of Guidance,Control and Dynamics,1994,17(3):553⁃560.
[18]Lu P.Entry Guidance and trajectory control for reusable launch vehicle[J].Journal of Guidance,Control and Dynam⁃ics,1997,20(1):143⁃149.
[19]Benito J,Mease K D.Nonlinear predictive controller for drag tracking in entry guidance[R].AIAA⁃2008⁃7350,2008.
[20]Richalet J,Rault A,Testud J L,et al.Model predictive heu⁃ristic control:application to robot manipulators[J].Automat⁃ica,1978,14(5):413⁃428.
[21]Lars G,Jurgen P.Nonlinear Model Predictive Control:Theo⁃ry and Algorithms[M].1st ed.Berlin:Springer,2011.
[22]Brunner,C W,Lu P.Skip entry trjectory planning and guid⁃ance[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1210⁃1220.
[23]Leslie F W,Justus C G.Earth global reference atmospheric model⁃2010 version[R].NASA/TM⁃2011⁃216467,2011.
[24]Lu P.Predictor⁃corrector entry guidance for low⁃lifting vehi⁃cles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1067⁃1075.
Skip Entry Guidance Using a Reference Trajectory for Lunar Module
DU Xin1,LIU Huilong1,HUANG Yuechen2
(1.High Speed Aerodynamics Institute,China Aerodynamics Research and Development Center,Mianyang 621000,China;2.College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)
In most of the mature skip entry guidance schemes,such as PredGuid and NSEG for CEV reentry,numerical predictor⁃corrector algorithm is used for the guidance of the first entry phase.Nu⁃merical predictor⁃corrector algorithm is of high accuracy and is flexible and autonomous,but it is too computation intensive to be applied online.A new guidance scheme using a reference trajectory for skip entry was proposed in this paper.The whole reference trajectory was obtained by off⁃line trajec⁃tory planning algorithm.In the first reentry phase,a nonlinear predictive control algorithm is used to track the drag⁃versus⁃energy profile.The predicted tracking error was expressed as a truncated Tay⁃lor series dependent on the control.The control was then selected to minimize a cost function related to the predicted error.In the second reentry phase,the reference trajectory was tracked by a linear feedback control algorithm which was used in Apollo final phase.The gain coefficient of PID control⁃ler was obtained by interpolation.Finally,the new guidance scheme was tested by the simulation of 500 entry cases with all kinds of errors.Simulation results indicate that the new guidance has high accuracy and notable robustness.
lunar return;skip entry;guidance using a reference trajectory;nonlinear predictive control;linear feedback control
V412.4
A
1674⁃5825(2016)06⁃0766⁃08
2016⁃05⁃10;
2016⁃11⁃04
国家自然科学基金(11372345)
杜昕(1985-),男,博士,助理工程师,研究方向为飞行器轨迹优化与制导控制。E⁃mail:232783682@qq.com

