载人登月地月转移轨道方案综述
彭祺擘,张海联
(载人航天总体研究论证中心,北京100094)
载人登月地月转移轨道方案综述
彭祺擘,张海联
(载人航天总体研究论证中心,北京100094)
在总结国内外月球探测地月转移轨道研究进展与现状的基础上,从整体上研究了地月转移轨道的设计模型及设计约束,分析了不同类型地月转移轨道的特点及适用性。结合载人登月飞行任务特点,讨论了可满足载人登月任务约束的轨道类型及方案,并通过仿真计算和对比现有转移轨道研究结论,分析了不同类型轨道的飞行时间、能量消耗、月面可达区域等特性,提出了应用建议,可为载人登月任务地月转移轨道方案深入研究提供参考。
载人登月;地月转移轨道;设计约束;地月平动点;自由返回轨道
1 引言
月球转移轨道具有距离远、时间长的特点,它的设计合理与否直接关系着载人登月工程任务实施的代价乃至成败。因此分析地月转移轨道的类型及其特性十分必要,可使我们了解地月转移轨道的内在规律、某些关键参数的影响特点等,对载人登月工程方案的制定具有指导意义。
目前有大量文献对地月转移轨道进行了研究,大多是以某一特定任务为背景,建立轨道设计动力学模型,对满足一定设计约束条件的轨道进行设计,并分析其相关特性。国外研究开始于上世纪50年代阿波罗任务前,经过半个多世纪的积累,形成了大量研究成果:例如,Penzo[1]、Dal⁃las[2]、Gibson[3]等基于圆锥曲线拼接模型研究了自由返回轨道的设计方法及轨道特性;Miele[4]、Schwaniger[5]、Jesick[6]等基于限制性三体模型,研究了地月转移轨道的最优设计问题;Baoyin等[7]研究了地月拉格朗日点附近和主要星体表面的转移轨道特性与其存在类型;Kluever等[8]对电推力情况下的地月转移轨道燃料优化问题进行了研究。
国内地月转移轨道研究始于20世纪90年代初。黄诚等[9]研究了动力学与运动学约束条件下的高精度轨道设计方法;郗晓宁等[10⁃11]利用双二体模型,对不同类型的地月转移轨道进行了设计和特性分析;刘林等[12⁃13]利用限制性三体模型对地月平动点特性进行了详细研究,并对利用平动点转移的轨道做了设计和分析;徐明等[14]对小推力地月低能转移轨道进行了设计和研究;宝音贺西等[15]对载人登月不同阶段的轨道问题进行了评述。
本文在借鉴国内外相关研究成果的基础上,进一步分析不同类型地月转移轨道的特性,主要针对载人登月任务,对满足约束条件的轨道方案进行研究,以为实际任务轨道方案选取及载人登月地月转移轨道深入研究提供参考。
2 地月转移轨道设计模型
2.1 轨道设计约束
载人登月对轨道设计的要求比无人月球探测更为严格,因此地月转移轨道的设计需要满足一系列约束条件,主要有工程带来的约束和轨道本身的约束[16]。
2.1.1 工程约束
工程约束主要包括飞行时间约束和速度增量约束。受环控生保条件限制,载人登月任务一般要求地月转移飞行时间t不能太长;另外受飞行器能力的限制,发动机所能提供的地月转移速度增量 Δv有限,因此轨道设计时要求满足式(1)[17]:
其中,Tmax为地月转移所能允许的最长飞行时间,ΔVmax表示地月转移过程飞行器推进系统所能提供的最大速度增量。
2.1.2 轨道约束
地月转移轨道的设计主要受飞行器近地出发轨道和月球到达轨道参数的限制。
1)近地轨道出发条件约束
受测控、发射场、运载能力等条件的约束,飞行器的地球出发轨道往往不能任意选取,会受到一些制约,主要包括轨道倾角和轨道高度约束。
受发射场位置限制,地球出发轨道倾角iE一般要大于发射场纬度ϕLaunch,如式(2):

考虑到轨道衰减问题及运载火箭能力限制,飞行器地月转移出发轨道高度rE一般要满足一定条件,如式(3):

其中,rEmin与rEmax为近地出发停泊轨道允许的最小高度和最大高度。
2)环月轨道到达条件约束
因为受月面着陆点位置、月面停留时间、交会对接等的限制,要求地月转移轨道的近月点必须满足环月轨道参数的约束,主要包括:轨道高度约束、轨道倾角约束、升交点赤经约束[16]。
(1)轨道高度约束
要求地月转移轨道近月点高度要大于目标环月轨道高度,又不能距离月球太远,以便通过合适的变轨策略将航天器送入预定环月轨道,如式(4):
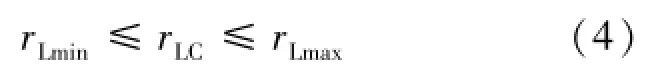
其中:rLC为地月转移轨道的近月距,rLmin为目标环月轨道高度,rLmax为地月转移轨道近月距允许的最大值。
(2)轨道倾角约束
为节省月面着陆的能量消耗,一般要求月面着陆器的着陆过程为共面转移[18],因此环月轨道的选择必须要能够覆盖月面着陆区,同时受任务规模限制,载人登月一般采用环月轨道交会对接的模式,即任务完成后月面着陆器需上升与环月轨道的环月航天器完成交会对接[19]。因此,当月面活动时间较长时(几天),则必须要对环月轨道做出合理设计,从而减少着陆器上升时与在轨环月航天器的异面差,节省上升交会燃料消耗。
由于存在应急等状况,月面停留时间往往存在不确定性,在实际中一般设计一个最佳环月轨道,使得着陆器在月面活动期间任何时刻上升,它与环月航天器交会对接时的异面差达到最小。
以月面活动时间不大于7天为例,通过设计环月轨道倾角,使得环月交会的异面差与上升时间满足图1的关系[18]。
从图中可以看出,设计的最佳环月轨道(图中实线),虽然在月面停留7天后使得着陆器上升时与目标环月轨道的异面差最大,但与不考虑月面停留时间不确定性的环月轨道(图中虚线)相比,其异面差峰值会大大减小,在工程实际中,只需着陆器具备这一最大异面差调整能力即可实现任意时刻上升。根据这一设计策略,下面给出最佳环月轨道倾角的求解方法。
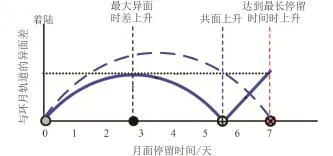
图1 月面停留时间与环月轨道交会异面差的关系[18]Fig.1 Relationship between lunar surface stay time and magnitude of plane change wedge angle for RVD[18]
如图2所示,设月面停留期间,着陆器与环月轨道航天器的最大异面差为W,则最佳环月轨道倾角iL、着陆点纬度ϕP和月面活动时间t应满足式(5)[18]。

图2 最佳环月轨道倾角与着陆点纬度的关系Fig.2 Relationship between LLO inclination and the latitude of lunar landing site
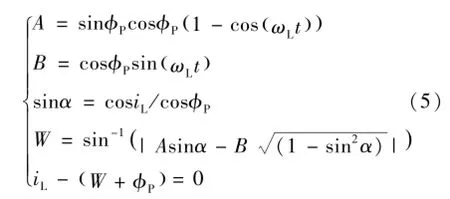
利用迭代法对上式进行求解,即可得到满足约束的最佳环月轨道倾角。需要指出的是,这里并未考虑由于摄动导致环月轨道升交点进动带来的影响,在实际设计中,需将此量与月球自转叠加综合考虑。
(3)轨道升交点约束
环月轨道在月固系下的升交点经度ΩL可根据轨道倾角和着陆点经纬度确定,设着陆点经度为λP,则有式(6):
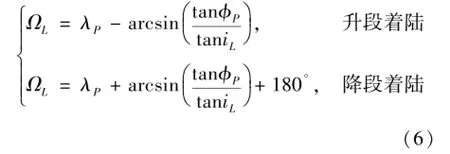
2.2 轨道设计模型
在轨道设计中,根据设计精度要求常会采用到不同的数学模型,地月转移轨道设计最为常用的模型主要有双二体模型、限制性三体或四体模型、高精度模型等。
2.2.1 双二体模型
双二体模型是研究地月飞行中常用的简化模型,它引进引力影响球的概念,把复杂的三体问题转化为二体问题。在双二体假设下,地月转移轨道分为两段。首先是位于月球影响球之外的地心段,此段忽略月球引力,轨道为地心圆锥曲线;然后是月球影响球内的月心段,此段忽略地球引力,轨道为月心圆锥曲线;在影响球边界上,将两段圆锥曲线拼接为一个整体[10]。
该模型一般认为月球是绕地心作匀速圆周运动,速度约为1.018 km/s,但实际月球是绕地球作椭圆运动,轨道偏心率约0.0549。在偏心率作用下,实际地月距与该假设下的地月距最大差约20 000 km,最大速度差约60 m/s。尽管这种误差对于地心段而言仅为飞行距离的6%左右,但对于月心段其误差则已经超过月球影响球半径的30%[20],因此该模型存在较大误差。为弥补这一缺陷,可在轨道设计过程中,将所涉及到任何时刻的月球位置和速度均以行星/月球历表计算得到,这样可以大大提高求解精度[21]。
2.2.2 限制性四体模型
由于飞行器的质量与地球、月球、太阳的质量相比,小到可以忽略的程度,因此,在地月转移使命分析与初步设计中,可以应用限制性四体问题。运动方程的一般形式表示如式(7)[22]:

其中,R为飞行器的地心位置矢量,R1为飞行器的月心位置矢量,R2为飞行器的日心位置矢量,RL为月心的地心位置矢量,RS为日心的地心位置矢量,μE、μL、μS分别为地、月、日的引力常数。
假设地、月、日共面运动,且地月之间的距离以及太阳离地月系统质心的距离均为常量。建立地月旋转坐标系O-xyz,原点位于地月系统的质心,x轴为地月连线,由原点指向月球方向为正方向,y轴在地月轨道平面内,由x轴逆时针旋转90°形成,z轴与其构成右手系。取下列无量纲化单位制:长度单位为地月平均距离,质量单位为地月质量之和,时间单位为T=P/(2π)=3.751897869×105s,其中P为地月会合周期。在该单位系中,牛顿引力常数为1。在上述坐标系中,飞行器地月转移的运动方程如式(8)[22]:
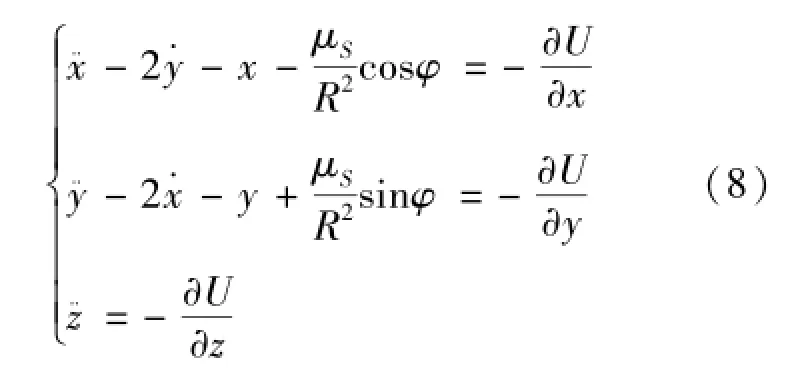
式中变量定义如式(9):
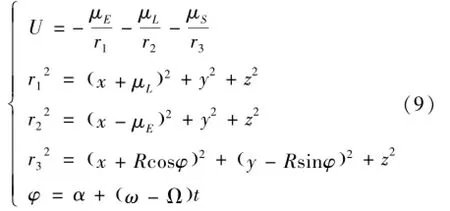
其中:ω为地球与月球绕坐标系原点的角速度;Ω为太阳绕原点的角速度;α为初始太阳方位角;R为太阳距离地月系统质心的距离。
该模型考虑了飞行器地月飞行受到的主要引力,求解精度相对较高。另外,限制性三体模型还被主要用于求解和分析地月平动点相关轨道[23]。
2.2.3 高精度模型
当计算精确的地月转移轨道时,需要对飞行器转移过程所受的摄动力做出分析,从而给出高精度的轨道设计模型。从轨道计算而言,飞行器的地月转移动力学方程可以建立在地心天球坐标系下,也可以建立在月心天球坐标系下,具体计算中需要根据实际情况来选择中心体。
当飞行器的动力学方程建立在地心天球坐标系中时,其形式如式(10)[10]:
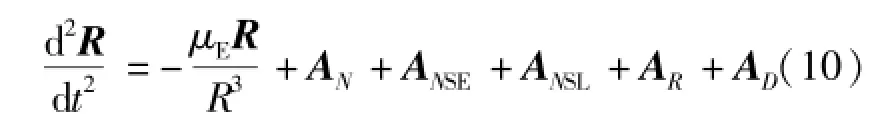
其中:AN为N体引力摄动加速度;ANSE为地球非球形摄动加速度;ANSL为月球非球形摄动加速度;AR为光压摄动加速度;AD为大气阻力摄动加速度。
该模型考虑了飞行器的各种受力因素,求解精度高,但计算量较大,一般在数值求解计算中采用。
3 地月转移轨道类型
常用的地月转移方式主要有四类:霍曼转移方式,通过共线平动点L1走廊的转移方式,弱稳定边界(WSB)转移方式和小推力转移方式。
3.1 霍曼转移方式
霍曼转移方式主要是采用两脉冲轨道机动来实现地月轨道转移,其飞行流程大致如下:登月飞行器完成近地任务后选择合适的时机,从近地停泊轨道出发,在出发点施加一个速度冲量,将飞行器推入奔月轨道;当到月球附近时,施加一个反向速度冲量,使其进入月球轨道(包括环月轨道或月球附近的平动点轨道),如图3所示。
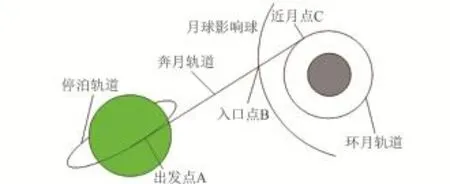
图3 霍曼转移方式示意图Fig.3 Schematic diagram of Hohman transfer trajectory
采用这种类型地月转移轨道到达月球的方式有两种:长程到达和短程到达。长程到达是指地月飞行时间大于地月转移地心轨道的半个周期,即到达月球时,真近点角f>π;短程到达是指地月飞行时间小于地月转移地心轨道的半个周期,即到达月球时,真近点角f≤π。图4给出了某一算例中以不同方式到达月球的地月转移速度增量与飞行时间的关系。图中下方曲线表示短程到达,上方曲线表示长程到达[16]。
从图中可以看出,长程到达时,飞行时间随着转移速度增量的增加而增加,且转移时间都在5天以上。因此对于长程到达来说,无论从时间还是能量上都不是最省的,并不适合于载人登月任务。
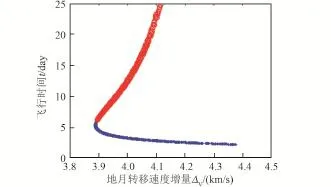
图4 长程到达和短程到达速度增量与飞行时间的关系[16]Fig.4 The relationship between transfer Δv and transfer time in differen tarriving modes[16]
采用霍曼转移方式实现奔月任务,往往过程比较简单,对工程实施的要求相对较低,飞行时间较短,因此这类轨道也是国内外载人登月任务研究中被主要采用的转移轨道类型。
3.2 利用地⁃月L1点的转移方式
从近地停泊轨道上经变轨飞往月球的过渡,根据限制性三体问题的结论,只要过渡轨道初始速度使相应的Jacobi常数C≤C1(稍小于),此时原包围地球P1和P2月球的两个零速度面相接并从平动点L1处稍稍打开了一个“狭窄走廊”,如图5所示,登月飞行器就有可能在越过通道后实现地月转移。但这只是飞行器可以越过该通道后奔月的一个必要条件,并非充分条件,还要看转移轨道的起始状态[24]。
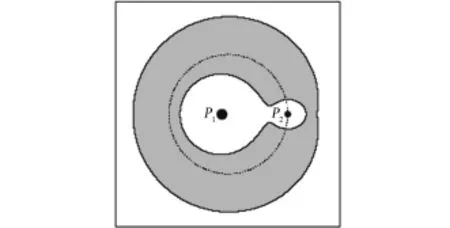
图5 Jacobi常数C≤C1时对应的飞行器运动可能区域[24]Fig.5 Accessible regions of the spacecraft C≤C1[24]
逆向积分L1点的稳定流形,如果该流形能与近地停泊轨道相交,则理论上在相交处变轨一次即可将飞行器由近地停泊轨道送入到稳定流形(实际是稳定流形所包裹的转移轨道),从而自动演化到月球引力范围内。但遗憾的是,当能量C在C1附近时,L1点的稳定流形不能到达距离地球很近的地方,它与地球的最近距离约为0.1个地月平均距离,因此对较低高度的近地停泊轨道而言,一次变轨将飞行器从近地停泊轨道送入到稳定流形是不可能的,需要一段过渡轨道连接,如图6所示。图中,PQ为连接弧段,P点在近地停泊轨道上,Q点在L1点的稳定流形上。变动稳定流形的能量以及P、Q点的具体位置,可以找到一条比较节省能量的转移轨道。由于在平动点L1处的能量开口很小,飞行器进入月球引力范围之后往往会自动被月球俘获。
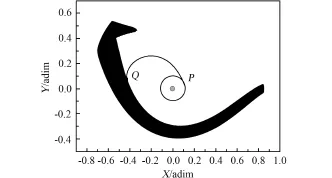
图6 连接弧段示意图Fig.6 Schematic diagram of the transition trajectory
通过以上分析可知,如果仅要求登月飞行器实现地月转移,而对目标环月轨道没有要求,则通过不变流形的转移方式比霍曼转移方式节省能量。但对于载人登月任务而言,环月轨道往往根据月面着陆区预先设计好,因此采用此类型地月转移轨道,必须施加额外的速度增量使得飞行器到达预定的环月轨道,即整个地月转移过程一般至少要通过施加三次脉冲完成,前两次分别在P点和Q点,第三次在近月点附近。正是由于要施加额外的速度增量来完成“搭桥”,所以此类轨道对于实施载人登月任务来说,能量往往并不节省。
图7给出了一条从高度为200 km的近地停泊圆轨道经两次变轨进入可转移轨道最终被月球俘获的轨道,下图是上图经过L1点后的放大(维持时间为1年)。
计算得到连接弧段PQ持续3.33天,从Q点开始到经过L1点耗时362.85天。如果要求进入的环月轨道高度为100 km,则整个转移过程需要施加的速度增量为 Δv=3102.11m/s+ 393.93 m/s+658.85 m/s=4154.89 m/s,该值比霍曼转移方式还要高,并且达到最优能耗需要耗费相当长的时间,因此从工程实施来看,发射飞行器时通过L1点的不变流形转移方式并不可取,因为这种转移轨道既耗时间又耗能量。
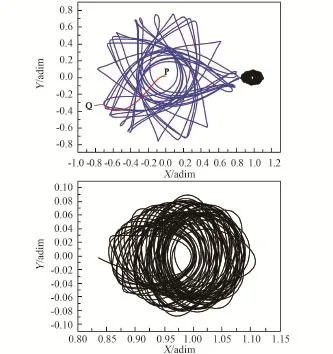
图7 一条通过L1点被月球俘获的转移轨道Fig.7 One transfer trajectory to be captured by the moon through L1 point
3.3 弱稳定边界转移方式
弱稳定边界转移轨道需要用到日⁃地系不变流形与地-月系不变流形相交的特性来实现地月转移。首先,飞行器可以先经由日-地系L1点或L2点的稳定和不稳定不变流形运行到地-月系的L2点之外,然后再经由地-月系的L2点稳定不变流形进入月球引力范围而被月球俘获[25],图8给出了两个限制性系统的不变流形相交示意图[24]。由于日-地系的稳定不变流形可以到达距地球很近的地方,因此可以直接从近地停泊轨道上一次变轨即将飞行器送入到日-地系的稳定不变流形,之后飞行器将经由日-地系的不稳定不变流形进入到地-月系的稳定不变流形而被月球俘获。如果对环月目标轨道有要求,则需要在目标轨道入轨点处再次变轨,整个过程只需要两次变轨。这类轨道最先由Belbruno等[26]给出,后来Koon等[27]利用不变流形解释了这类轨道的动力学机制。这类轨道通常称为月球弹道转移轨道(Lunar Ballistic Trajectories)或者弱稳定边界WSB(Weak Stability Boundary)转移轨道。
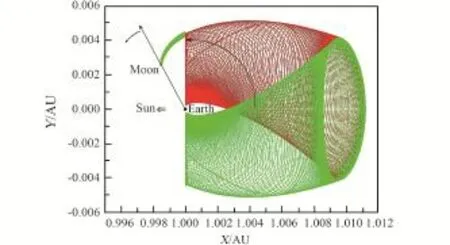
图8 日⁃地系的L2点附近的流形与地⁃月系L2点附近的流形的相交情形[24]Fig.8 Intersections between the invariant manifolds of thesun⁃earth L2 point and of the earth⁃moon L2 point[24]
Koon等设计WSB轨道的方法如下:首先计算两个限制性三体系统对应的不变流形的Poincaré截面,并研究它们的相交情形,从中选出一条拼接轨道,即一部分在日-地系对应的圆型限制性三体系统中,另一部分在地-月系对应的圆型限制性三体系统中,在连接处将这两者几何上拼接起来,然后在完整力模型下数值改进以得到实际的转移轨道[28]。通过初步估算可知,这种类型的转移轨道所需要的最小能量为3787 m/s,但这里忽略了飞行器由日-地系中能量为C′2的状态变为地-月系中能量为C2的状态所需的能量,因为在该处所需的能量随飞行器的位置不同而不同,所以真正的WSB轨道需要消耗的能量要略大于最优值3787 m/s。
图9给出了设计的一条WSB转移轨道在地心惯性系中的图像,闭合曲线为月球轨道。该转移轨道耗时102.04天,第一次变轨为3200.07 m/s,第二次变轨为647.63 m/s,总能耗为3847.70 m/s,近地停泊轨道高度为200 km,环月目标轨道高度为200 km。
虽然WSB转移轨道比传统的霍曼转移轨道要节省能量,但这样的转移轨道耗时过长,因此,这种类型的转移轨道也仅仅适用于对时间要求不高的月球探测任务[29]。
3.4 小推力转移方式
小推力转移是指采用推力较小的连续推力发动机,通过持续开机将登月飞行器送入月球轨道。该模式可以全程采用小推力转移,或者可与脉冲式推力结合实现转移,由于推力较小,其转移轨道呈现螺旋状[30⁃31],如图10所示。
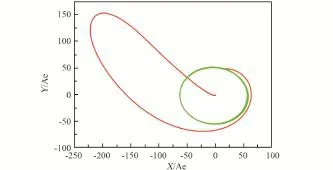
图9 地心惯性系中的WSB转移轨道Fig.9 WSB transfer trajectory in the earth inertial coordinate
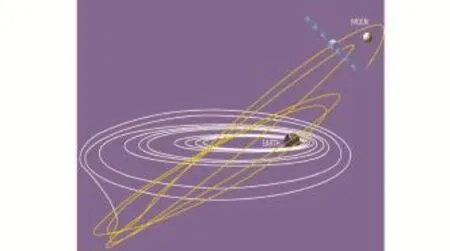
图10 小推力转移轨道示意图Fig.10 Schematic diagram of the low thrust transfertrajectory
利用该方式转移,飞行器在奔月过程中受到推力较小,一般需要耗费较长的时间,但小推力发动机一般采用新型的推进模式(如电推进),往往具有较高的比冲,因此会减轻飞行器燃料质量,但长的转移时间会导致航天员更多的消耗,倘若用在载人登月任务中,其实并不能对减轻登月飞行器的质量有太大帮助,往往安全性还更差,因此一般也不采用。
针对以上各种地月转移轨道类型,表1通过仿真计算进一步对能量消耗和飞行时间做出了比较。

表1 不同地月转移方式的比较Table 1 Comparision of different lunar transfer modes
综上,载人登月任务的奔月轨道采用大推力霍曼转移方式为宜,且应采用短程到达的方式。
4 载人登月地月转移轨道选择
通过上述分析可知,对于载人登月任务来说,由于受飞行时间、安全性、可靠性等约束,一般都采用大推力霍曼转移的地月转移轨道,对于该类轨道同样有不同方案,主要包括一般转移轨道方案、自由返回轨道方案和基于自由返回轨道的变轨方案等。
4.1 一般转移轨道
一般转移轨道最为简单,轨道设计只需要满足飞行时间、月面着陆区、测控等任务最基本的约束条件即可。
由于设计约束相对较少,此类轨道设计空间往往较大,其飞行时间约在2~5天左右,地月转移的能量消耗3.9~4.5 km/s,且基本可以到达任意环月轨道,覆盖不同月面着陆区,在实际任务中可根据工程约束选择最优的飞行轨道。但采用一般转移轨道,倘若飞行器在地月转移过程中发生故障,在不进行轨道机动的前提下,将无法返回地球,因此其安全性相对较低。鉴于这一原因,一般转移轨道往往被用于无人飞行器转移(如载人登月任务中的物资转移),或者是在经历多次飞行、任务非常成熟时的载人飞行器地月转移。
4.2 自由返回轨道
自由返回轨道是指登月飞行器在不进行环月制动时,可以不需要轨道机动或只需要很小的推力进行轨道修正就能返回地球的地月转移轨道,如图11所示。它是在地月转移过程中推力系统失效情况下飞行器所能安全返回地球的最省能量轨道,因此具有很高的安全特性[21]。

图11 自由返回轨道示意图[21]Fig.11 Schematic diagram of the free return trajectory[21]
根据飞行路径,自由返回轨道可以分为四类[32]:地心顺行绕月自由返回轨道、地心逆行绕月自由返回轨道、地心顺行非绕月自由返回轨道和地心逆行非绕月自由返回轨道。地心顺行轨道是指飞行器从地球停泊轨道出发时的速度方向与地球自转方向一致,逆行轨道则表示相反;绕月轨道是指地月转移轨道的近月点在月球背面,即飞行器绕过月球背面后返回地球,非绕月轨道则是指近月点在月球正面,即飞行器从月球正面利用月球引力转向后返回地球。非绕月自由返回轨道类似于3.1节提到的长程到达,飞行时间和能量消耗都会大于绕月自由返回轨道,因此并不适合于载人登月任务。另外,对于地心逆行轨道来说,由于其出发速度方向与地球自转速度方向相反,火箭在将飞行器送入预定轨道时所需要消耗的燃料更多,即运载能力损失更大,因此也一般不用于载人登月任务。在实际工程中一般只选用地心顺行绕月自由返回轨道作为载人登月任务的地月转移轨道。
自由返回轨道所需的最小速度增量一般要大于非自由返回轨道,其所能达到的环月轨道均为逆行轨道,倾角只能集中在相对白道160°~180°之间,且要求的近月距越小,所能到达的环月轨道与白道的夹角越小;进一步转化到月固系下,其所对应的月面着陆点纬度也只能在约±20°之间(这一值会随出发时刻的不同稍有变动,最大不超过±25°),如图12所示[16]。因此地月转移任务如果采用自由返回轨道,则不能实现全月面到达,只能到达低纬度区域。这与“阿波罗”任务时期所得到的结论相同,“阿波罗”前期任务都采用了自由返回轨道,因此其月面着陆点都选择在赤道附近[33]。

图12 自由返回轨道所到达的月面着陆区范围[16]Fig.12 Range of the lunar landing site[16]
4.3 基于自由返回轨道的中途变轨方案
自由返回轨道+中途变轨,亦称混合轨道,它是指飞行器沿自由返回轨道飞行一定时间后,确保飞行器不出现故障时,通过施加一次中途变轨,使其进入目标轨道,如图13所示[20]。
混合轨道可以使飞行器的月球轨道到达范围大大增加,几乎可达到任意轨道倾角和环月轨道高度(其中升交点不能任意取值,需与轨道倾角相对应)[21],但对于到达不同的环月轨道,其能量消耗代价不同,图14给出了到达不同环月轨道倾角,中途变轨所需的速度增量。图15进一步给出了变轨至环月极轨时,地月转移出发后不同时刻实施变轨所需的速度增量[21]。
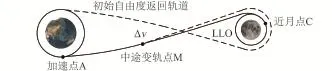
图13 混合轨道示意图[21]Fig.13 Schematic diagram of the hybrid trajectory[21]
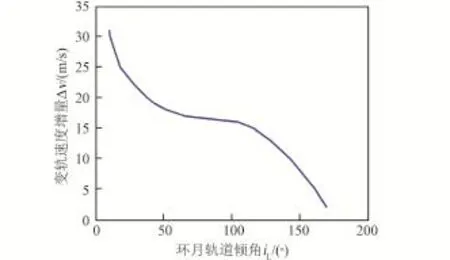
图14 环月轨道倾角对中途变轨速度增量的影响Fig.14 Influence of the lunar orbit inclination angel on the midway orbit maneuver Δv
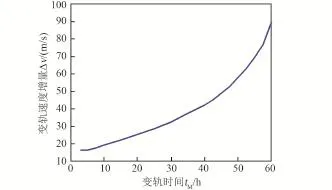
图15 变轨时刻对变轨速度增量的影响Fig.15 Influence of the orbit maneuver time on the orbit maneuver Δv
从图中可以看出,采用该方案,改变的轨道面倾角越大,所需要的速度增量越大;当到达同一目标环月轨道时,中途变轨时刻越早,所需的能量越小。
总的来说,该方案只需要较小的变轨速度增量(一般不大于100 m/s),就可实现月面不同纬度区域的探测,但当进行了中途轨道机动之后,地月转移轨道的自由返回特性就会被破坏,此时倘若飞行器出现故障,则必须要施加额外的速度增量才能使其返回地球,因此其安全性比自由返回轨道有所降低。
4.4 基于自由返回轨道的终端变轨方案
自由返回轨道+终端变轨是指飞行器首先沿自由返回轨道实现地月转移,到达月球附近后再通过轨道机动实现轨道面的改变,以进入目标环月轨道。在到达月球后,实现飞行器轨道面机动方式有很多种,但为节省能量,一般先将飞行器制动进入一个绕月大椭圆过渡轨道,然后在远月点通过施加脉冲实现轨道面的改变,因此采用这种变轨方案,环月制动往往需要施加3次速度增量,第一、三次脉冲主要用于改变轨道长半轴,第二次脉冲主要用于轨道面改变,其飞行过程如图16所示[18]。
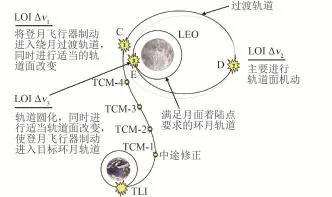
图16 自由返回轨道+终端变轨飞行示意图[18]Fig.16 Schematic diagram of the terminal orbit ma⁃neuver flight based on free return trajecto⁃ry[18]
该方案同样可以使飞行器达到任意环月轨道倾角,但变轨至不同环月轨道倾角时,其能量消耗代价相差较大,图17给出了到达不同环月轨道倾角,终端变轨所需的速度增量。图18进一步给出了变轨至环月极轨时,完成终端三脉冲变轨所消耗时间对变轨速度增量的影响[21]。
从图中可以看出,采用该方案,同样改变的轨道面倾角越大,所需要的速度增量越大;当到达同一目标环月轨道时,三脉冲变轨飞行时间越长(即过渡椭圆轨道半长轴越长),所需的能量越小。
自由返回轨道+终端变轨这一方案是在飞行器到达近月点后才实施轨道机动,在奔月过程中出现任何故障都可以实现无动力返回,因此其安全性相对较高,但这种变轨方案所消耗能量受轨道面差异的影响很大,倘若轨道面变化很大,则其需要的能量较大(远大于中途变轨方案);另外由于利用了大椭圆过渡轨道实现轨道面机动,其飞行时间会大大延长,如利用100×9000 km的绕月过渡轨道实现轨道面机动,则飞行时间要比标准飞行时间增加约7小时。

图17 环月轨道倾角对终端变轨速度增量的影响Fig.17 Influence of the lunar orbit inclination angel on the terminal orbit maneuver Δv

图18 三脉冲变轨时间对变轨速度增量的影响[21]Fig.18 Influence of the orbit maneuver time on the terminal orbit maneuver Δv[21]
5 结论
本文对地月转移轨道的类型、求解模型及轨道特性进行了详细分析,通过分析可知,目前对于载人登月任务而言,最佳的轨道类型仍为大推力霍曼转移方式,该类型轨道中不同的转移轨道方案的对比如表2所示。其中自由返回轨道及基于自由返回轨道的终端变轨方案安全性较高,适用于早期的载人登月任务;基于自由返回轨道的中途变轨方案可在任务取得一定成熟经验后采用;一般转移轨道可用于货物运输或任务非常成熟时的载人飞行。工程中实际采用哪类轨道方案,还需要结合整个系统的安全可靠性及飞行器的能力等进行综合权衡。

表2 不同地月转移轨道方案的比较Table 2 Comparision of different lunar transfer trajec⁃tory schemes
(
)
[1]Penzo P.An analysis of free⁃flight circumlunar trajectories[C]//AIAA Astrodynamics Conference,New Haven,Con⁃necticut,1963.
[2]Dallas SS.Moon⁃to⁃Earth trajectories[C]//AIAA Astrody⁃namics Conference,New Haven,Connecticut,1963.
[3]Gibson T.Application of the matched conic model in the stud⁃y of circumlunar trajectories[R].NASA 70⁃35798,1963.
[4]Miele A.Theorem of image trajectories in the Earth⁃Moons⁃pace[J].Acta Astronautica,1960,6(51):225⁃232.
[5]Schwaniger A J.Trajectories in the Earth⁃Moon space with⁃symmetrical free return properties[R].NASA Technical Not⁃eD⁃1883,Washington DC,1963.
[6]Jesick M,Ocampo C.Automated generation of symmetric lu⁃nar free⁃return trajectories[J].Journal of Guidance,Control and Dynamics,2011,34(1):98⁃106.
[7]Baoyin H,McInnes C.Trajectories to and from the lagrange⁃points and the primary body surfaces[J].Journal of Guid⁃ance,Control αnd Dynamics,2006,29(4):998⁃1003.
[8]Kluever C A,Pierson B L.Optimal Earth⁃Moon trajecto⁃riesusing nuclear electric propulsion[J].Journal of Guid⁃ance,Control and Dynamics,1997,20(2):239⁃245.
[9]黄诚,胡小工,李鑫.满足一定约束条件的登月飞行轨道设计[J].天文学报,2001,42(2):161⁃172.Huang Cheng,Hu Xiaogong,Li Xin.Lunar⁃landing trajectory designing under certain constraints[J].Acta Astronomica Sinica,2001,42(2):161⁃172.(in Chinese)
[10]郗晓宁,曾国强,任萱,等.月球探测器轨道设计[M].北京:国防工业出版社,2001:51⁃129.Xi Xiaoning,Zeng Guoqiang,Ren Xuan,et al.Orbit Design of Lunar Probe[M].Beijing:National Defense Industry Press,2001:51⁃129.(in Chinese)
[11]曾国强,任萱,郗晓宁.快速设计月球卫星转移轨道的一种代数方法[J].国防科技大学学报,2000,22(2):1⁃6.Zeng Guoqiang,Ren Xuan,Xi Xiaoning.An algebraic meth⁃od for fast design of lunar satellite transfer trajectory[J].Journal of National University of Defense Technology,2000,22(2):1⁃6.(in Chinese)
[12]刘林,王歆.月球探测器轨道力学[M].北京:国防工业出版社,2006:15⁃50.Liu Lin,Wang Xin.An Orbital Dynamics of Lunar Probe[M].Beijing:National Defense Industry Press,2006:15⁃ 50.(in Chinese)
[13]刘林,侯锡云,王海红.关于共线平动点的特征及其在深空探测中的应用[J].天文学进展,2006,24(2):174⁃182.Liu Lin,Hou Xiyun,Wang Haihong.On Characteristics of Collinear Libration Points and Their Application in Deep Space Exploration[J].Progress in Astronomy,2006,24(2):174⁃182.(in Chinese)
[14]徐明,徐世杰.小推力航天器的地月低能转移轨道[J].航空学报,2008,29(4):781⁃787.Xu Ming,Xu Shijie.Low⁃energy trajectory from Earth to Moon for low⁃rhrust spacecraft[J].Acta Aeronautica et Astro⁃nautica Sinica,2008,29(4):781⁃787.(in Chinese)
[15]宝音贺西,李京阳.载人登月轨道研究综述[J].力学与实践,2015:36(6):665⁃673.Baoyin Hexi,Li Jingyang.Review of trajectory design for manned lunar mission[J].Mechanics in Engineering,2015:36(6):665⁃673.(in Chinese)
[16]Peng Q B,Shen H X,Li H Y.Free return orbit design and characteristics analysis for manned lunar mission[J].Sci Chi⁃na Tech Sci,2011,54(12):3243⁃3250.
[17]彭祺擘,李海阳,李桢等.从空间站出发的奔月轨道设计[J].国防科技大学学报,2009,31(2):25⁃30.Peng Qibo,Li Haiyang,Li Zhen,et al.Trans⁃lunar trajecto⁃ry design of lunar probe launched from space station[J].Journal of National University of Defense Technology,2009,31(2):25⁃30.(in Chinese)
[18]Condon G L.Lunar orbit insertion targeting and associated outbound mission design for lunar sortie missions[R].Flt⁃Dyn⁃CEV⁃06⁃72,2007.
[19]彭祺擘,李桢,李海阳.载人登月飞行方案研究[J].上海航天,2012(5):14⁃19.Peng Qibo,Li Haiyang,Li Zhen.Analysis on manned lunar mission flight mode[J].Aerospace Shanghai,2012(5):14⁃19.(in Chinese)
[20]黄文德,郗晓宁,王威.基于双二体假设的载人登月混合轨道特性分析及设计[J].国防科技大学学报,2010,32(4):61⁃67.Huang Wende,Xi Xiaoning,Wang Wei.Characteristics anal⁃ysis and desing of hybrid trajectory for manned lunar landing mission based on double two⁃body model[J].Journal of Na⁃tional University of Defense Technology,2010,32(4):61⁃67.(in Chinese)
[21]彭祺擘.考虑应急返回能力的载人登月轨道优化设计及特性分析[D].长沙:国防科技大学,2012.Peng Qibo.Optimal Trajectory Design and Characteristics A⁃nalysis for Manned Lunar Landing Mission with Emergency Return Capability[D].Changsha:National University of De⁃fense Technology,2012.(in Chinese)
[22]戚发轫,朱仁璋,李颐黎.载人航天器技术[M].北京:国防工业出版社,2003:42⁃44.Qi Faren,Zhu Renzhang,Li Yili.Manned Spacecraft Tech⁃nology[M].Beijing:National Defense Industry Press,2001:42⁃44.(in Chinese)
[23]刘林,刘慧根.地月系中探测器定点在三角平动点附近的位置漂移及其控制问题[J].宇航学报,2008,29(4):1222⁃1227.Liu Lin,Liu Huigen.Orbit drift and control of the spacecraft around the triangular libration points in the Earth⁃Moon system[J].Journal of Astronautics,2008,29(4):1222⁃1227.(in Chinese)[24]侯锡云,刘林.共线平动点的动力学特征及其在深空探测中的应用[J].宇航学报,2008,29(3):736⁃747.Hou Xiyun,Liu Lin.The dynamics and applications of the collinear libration points in deep space exploration[J].Jour⁃nal of Astronautics,2008,29(3):736⁃747.(in Chinese)
[25]龚胜平,李俊峰,宝音贺西等.基于不变流形的登月轨道设计[J].应用数学和力学,2007,28(2):183⁃190.Gong Shengping,Li Junfeng,Baoyin Hexi,et al.Lunar landing trajectory design based on invariant manifold[J].Ap⁃plied Mathematics and Mechanics,2007,28(2):183⁃190.(in Chinese)
[26]Belbruno E A.Lunar capture orbits,a method of constructing earth moon trajectories and the lunar gas mission[C]//19th AIAA/PGLR/JSASS International Electric Propulsion Confer⁃ence,Colorado Springs,Colorado,May,1987.AIAA⁃87⁃1054.
[27]Koon W S,Lo M W,Marsden J E,etal.Low energy transfer to the moon[J].Celestial Mechanics and Dynamical Astrono⁃my,2001,81(1):63⁃73.
[28]徐明.平动点轨道的动力学与控制研究综述[J].宇航学报,2009,30(4):1299⁃1313.Xu Ming.Overview of orbit dynamics and control for libration point orbits[J].Journal of Astronautics,2009,30(4):1299⁃1313.(in Chinese)
[29]何巍,徐世杰.地月低能转移轨道设计方法研究[J].宇航学报,2006,27(5):965⁃969.He Wei,Xu Shijie.Research on low energy trajectory design method between Earth and Moon[J].Journal of Astronautic,2006,27(5):965⁃969.(in Chinese)
[30]王劼,崔乃刚,刘暾.定常幅值小推力登月飞行器轨道研究[J].航空学报,2001,22(1):6⁃9.Wang Jie,Cui Naigang,Liu Dun.On constant⁃amplitude low⁃thrust lunar probe trajectories[J].Acta Aeronautica et Astronautica Sinica,2001,22(1):6⁃9.(in Chinese)
[31]王劼,崔乃刚,刘暾.小推力登月飞行器轨道初步研究[J].飞行力学,2000,18(2):46⁃49.Wang Jie,Cui Naigang,Liu Dun.Preliminary study on mini⁃mum⁃fuel lunar probe trajectories[J].Flight Dynamics,2000,18(2):46⁃49.(in Chinese)
[32]白玉铸.载人登月轨道设计相关问题研究[D].长沙:国防科技大学,2010.Bai Yuzhu.Research on Trajectory Design for Manned Lunar Landing Mission[D].Changsha:National University of De⁃fense Technology,2010.(in Chinese)
[33]Head J W.Scientific rationale summaries for Apollo candidate lunar exploration landing sites[R].NASA⁃CR⁃109867,1970.
Review of Lunar Transfer Trajectory Modes for Manned Lunar Mission
PENG Qibo,ZHANG Hailian
(Manned Space System Research Center,Beijing 100094,China)
Based on the status and research progress of the earth⁃lunar transfer trajectory in China and abroad,the design model and constraints of the earth⁃lunar transfer trajectory were studied and the characteristic and adaption of different types of trajectories were analyzed in this paper.Accord⁃ing to the features of human lunar exploration mission,the types of the lunar transfer trajectory and the design schemes were discussed.Simulation was conducted to compare the available trajectory re⁃search results,then the flight duration,energy consumption and lunar landing destination for differ⁃ent types of trajectories were analyzed.Finally,suggestions on human lunar exploration mission's trajectory design were proposed which may serve as a reference for the further study.
mannedlunar mission;earth⁃lunar transfer trajectory;design constraints;earth⁃lunarli⁃bration point;free return trajectory
V412.4
A
1674⁃5825(2016)06⁃0663⁃10
2016⁃05⁃31;
2016⁃09⁃11
彭祺擘(1982-),男,博士,助理研究员,研究方向为载人登月总体任务分析与设计。E⁃mail:poochie003@163.com

