地月L2中继星或月球轨道器对月球背面着陆器多普勒定位精度分析
雷文英,蒙艳松,雷文华,边 朗,王 瑛
(1.中国空间技术研究院西安分院,西安710100;2.西藏大学理学院,拉萨850000)
地月L2中继星或月球轨道器对月球背面着陆器多普勒定位精度分析
雷文英1,蒙艳松1,雷文华2,边 朗1,王 瑛1
(1.中国空间技术研究院西安分院,西安710100;2.西藏大学理学院,拉萨850000)
针对地面站无法对月球背面着陆器定位的问题,分别对月球背面着陆器利用月球轨道器上行信号和地月L2中继星上行信号的多普勒对其定位的两种模式进行了研究。在月固坐标系下,理论分析了两种模式下轨道器的多普勒定位精度,以及几何精度因子及频率稳定度对定位精度的影响。在STK软件中对两种定位模式建模,利用其导出的星历数据定量评估了两种定位模式下着陆器的定位精度,讨论了应用两种定位模式应满足的时间约束和空间约束条件,同时定量分析给出了不同载频、不同观测时间长度下,着陆器时钟应该满足的频率稳定度。
地月L2点;月球轨道器;月球着陆器;多普勒定位;精度分析
1 引言
月球探测和载人登月不但有利于开发利用月球和太空资源,而且可促进航天技术的创新和发展,推动科技进步[1⁃3]。对于月球正面着陆的月球探测器,如嫦娥三号,其月面软着陆后着陆器和巡视器的定位可利用地面跟踪站通过测距、测速和甚长基线干涉测量(Very Long Baseline Interfer⁃ence,VLBI)来实现[4]。由于月球对无线电信号的遮挡,地面跟踪站很难对月球背面着陆的着陆器和巡视器进行观测,不能直接定位[5]。然而,月球背面的资源同样具有重大的探测价值,载人月球探测器在对地不可见的月球背面开展空间科学领域观测具有重要意义[6]。对月球背面轨道器和巡视器的导航定位是顺利完成月球对地不可见区域月面探测任务的基本保障,而月球背面着陆器和巡视器的月面导航定位是开展探月任务亟待解决的关键问题之一。
对月球背面着陆器和巡视器的定位问题,以往依靠地面支持的地基测量定位法无法直接使用[6]。从国内外研究进展来看,目前适用于月球背面的着陆器和巡视器的导航定位方法主要包括三种:天文导航定位、惯性导航定位和光学导航定位。天文导航基于天体位置已知的前提条件,通过测量天体相对于导航用户参考基准面的方位角和仰角计算导航用户的方位和位置[7],局限性在于其位置解算复杂费时、定位精度较差[6⁃8]。惯性导航定位是结合外界提供的初始姿态、位置和速度信息,通过对陀螺仪进行角速度积分解算导航用户的当前姿态,通过当前姿态和加速度信息获得导航用户的惯性加速度,对其进行一次和二次积分解算出导航用户的速度和位置信息[9]。局限性在于陀螺仪的漂移误差和加速度计的零偏误差会随着时间的增长而放大,在没有外界提供的周期定位校正的情况下,不适合长时间导航定位[10]。光学导航利用导航相机获得月球表面参考特征点的图像,利用激光测距仪测得导航用户与参考特征点的距离,采用“图像+距离”的工作方式得到导航用户相对于参考特征点的姿态、相对位置和速度[11]。局限性在于其信息处理速度慢,作用距离短且不能提供导航用户的绝对位置信息[6,11]。
本文针对月球背面着陆器和巡视器无法利用地面测距和VLBI测时延的方式对其进行导航定位的问题,提出测量月球导航用户与地月L2中继星或月球轨道器上行信号多普勒信息,结合在月固坐标系下L2中继星或月球轨道器的位置和速度信息实现对月球背面轨道器和着陆器的导航定位,对该定位方法的定位精度进行理论推导和数值仿真计算,在STK中对两种应用场景进行建模,定量分析了两种定位方案下对着陆器的多普勒定位精度,以及要达到优于100 m定位精度需要满足的前提条件。
2 月球背面着陆器多普勒定位模式
月球背面着陆器的定位在原理上可通过环月星座采用类似于GPS的定位模式实现[5]。但环月星座的成本较高、测控复杂,且目前处于研究阶段[5],不能满足当前阶段月球背面轨道器的定位需求。因此,本文研究一种利用月球轨道器或地月L2点中继卫星,实现对月球背面的着陆器进行导航定位的多普勒定位模式。
月球背面巡视器的月面定位和着陆器距离一般比较近,因此对其定位的方式比较类似。以下以着陆器的定位为例进行分析,其结果同样适用于巡视器的月面定位。
2.1 环月轨道模式
从目前国内外研究进展来看,月球背面着陆器的导航定位主要可采用环月轨道和地月L2点轨道两种模式[6]。环月轨道飞行器距离月面较近,运行速度快,但波束覆盖区域较小。图1给出了环月模式下,距月面100 km的环月轨道器对月面的覆盖示意图。

图1 环月轨道器的轨道和回归周期内的覆盖区域Fig.1 Circumlunar orbiter and its coverage over a regression period
图1表明环月轨道器在一个回归周期内可对月球背面的大面积区域进行有效覆盖。如果着陆器的着陆位置选在图1中轨道器在一个回归周期内没有覆盖到的区域,可通过调整轨道的升交点赤经,将覆盖区域移动到月球背面合适的位置。
2.2 地月L2轨道模式
地月L2点的中继星可实现对地不可见的月球背面和极地区域的长时间覆盖、观测和通信,其距月面的轨道高度较高,运行速度较慢,波束覆盖区域较大。图2展示了地月质心旋转坐标系[12]下的地月L1点和地月L2点,以及L2点附近的一条Halo轨道。从图2中可看出,L2点位于地月质心连线上,且位于月球背面,在地月L2点Halo轨道上运行的中继星可对月球背面进行覆盖,且不受月球的遮挡,与地球保持可视。
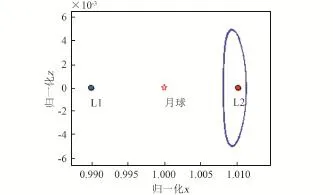
图2 地月L2点的Halo轨道Fig.2 Halo orbit around the Earth⁃Moon L2 point
图3给出了地月L2点中继星轨道和地、月之间相对位置的三维图,并给出了地月L2点中继星对月球背面的覆盖区域。
图3中,中继星的3 dB波束宽度设为10°,从图中可看出其可对月球背面和月球南极的大部分区域进行覆盖。因此,月球背面的着陆器可与地月L2中继星保持实时通信。
3 月球背面着陆器多普勒定位模型
对于月球背面着陆器的定位,在月固坐标系[13]中对其进行分析描述。地月L2中继星对月面的上行信号载频已知。着陆器在月球背面着陆后,设其在月固坐标系下的未知坐标为(x,y,z)T。在地月L2中继星的波束覆盖范围内,对上行信号的多普勒进行N次等间隔采样,采样间隔为Ts。以中继星为例,测量方程可表示为式(1):
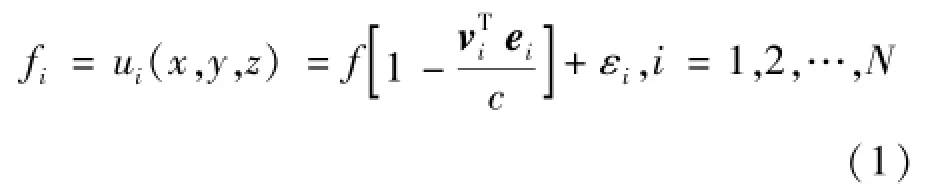
其中:fi表示第i次测量到的多普勒,vi是卫星速度,f是载频,c是光速,εi是多普勒测量噪声。着陆器与中继星之间的径向距离如式(2):
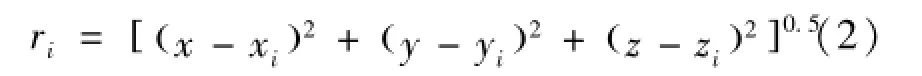
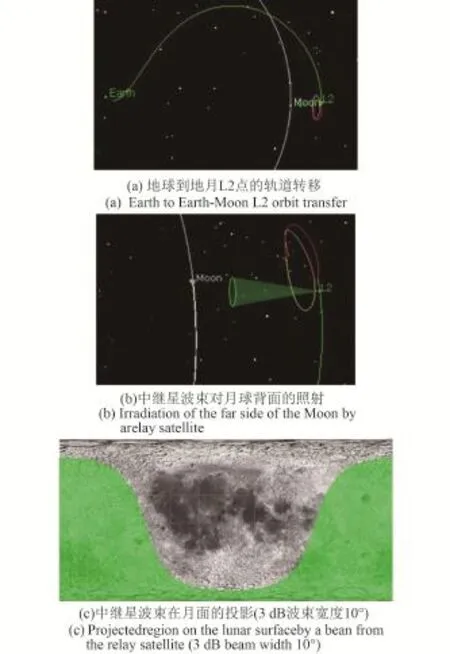
图3 中继星对月球背面的覆盖示意图Fig.3 Coverage area of the relay satellite
中继星和着陆器视线方向的单位矢量如式(3):
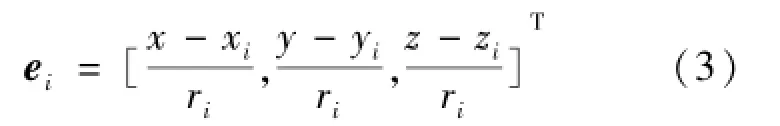
中继星在月固坐标系下的位置 (xi,yi,zi)T及速度vi=(vxi,vyi,vzi)T是已知的。未知量是着陆器的坐标(x,y,z)T。
考虑到月球的偏心率为零,着陆器天线架高h为已知量,着陆器位于月球表面的高程约束条件可表示为式(4):
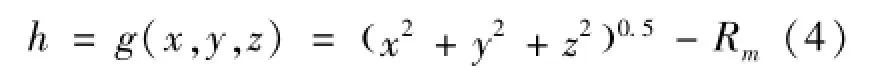
上式中月球半径Rm=1737.4 km[13]。
在式(1)中,选三个多普勒观测值和式(4)联立,即可实现对着陆器位置坐标(x,y,z)T的求解。然而,轨道器和着陆器之间的空间位置关系、接收机的频率稳定度、播发信号载频等因素均对定位误差有影响,因此需对这些误差源对定位精度的影响进行定量分析。
4 月球背面着陆器定位精度分析
4.1 几何精度因子对定位误差的影响
取式(1)中三个多普勒测量值,结合式(4),并对其取微分得到式(5):
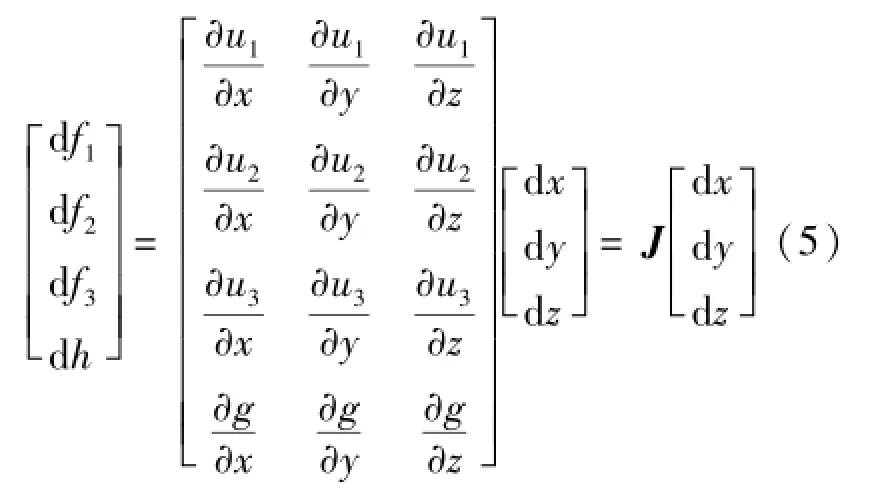
上式中J为雅可比矩阵,其中的各个元素取值分别可表示为式(6)~(12):
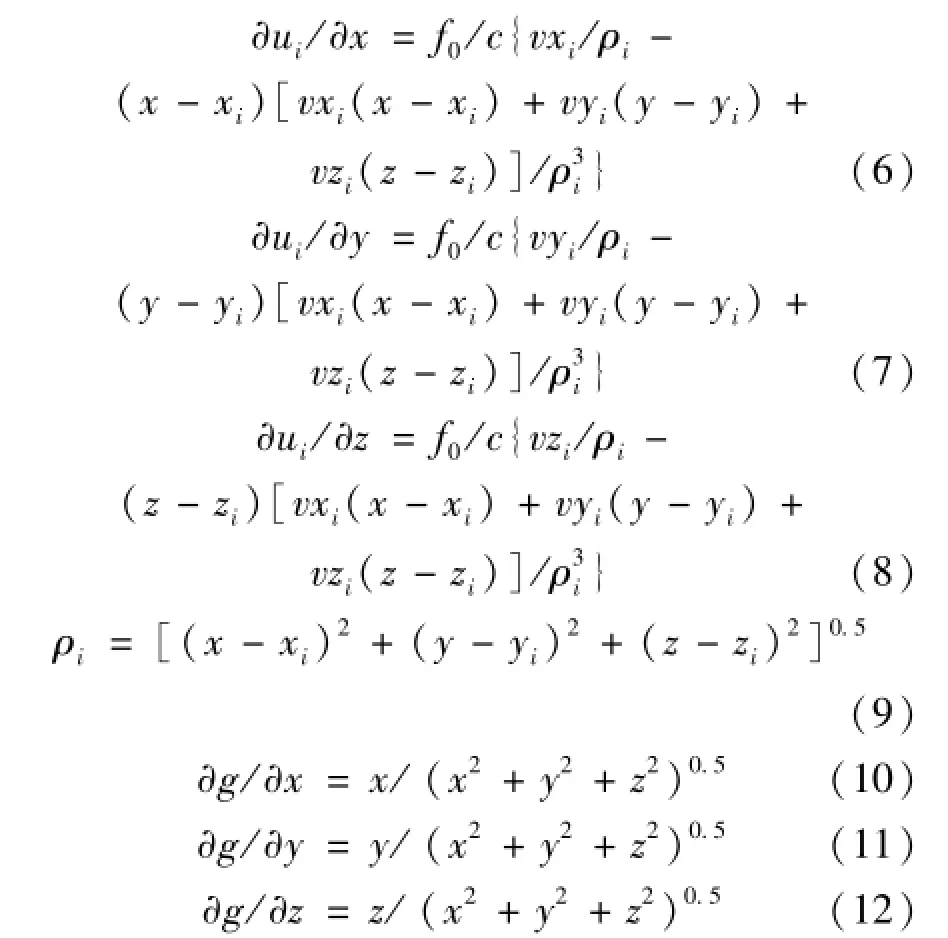
式中i=1,2,3。令dx=(dx,dy,dz)T,dy=(df1,df2,df3,dh)T,则存在关系如式(13):

式(10)~式(12)中∂g/∂x、∂g/∂y、∂g/∂z分别是式(4)关于着陆器三个坐标分量x,y,z的偏导数。
定位误差的协方差矩阵Pdx=E[dxdxT]可表示为式(14):
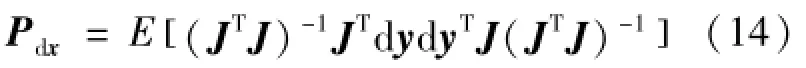
在高度z=h已知的条件下,dh=0。由于f1、f2、f3测量相互独立,令dy′=(df1,df2,df3)T,则代入式(14)可得式(15):
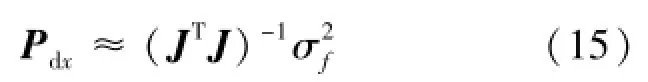
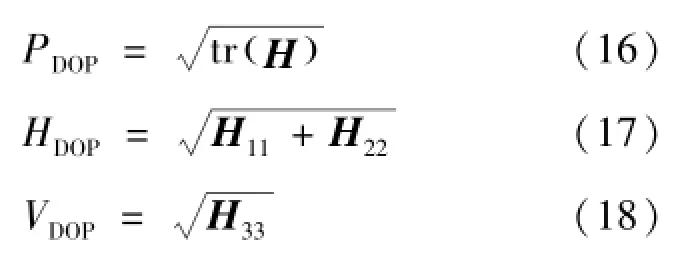
4.2 频率稳定度对定位误差的影响
式(16)~式(18)与多普勒测量无关,仅仅与轨道器的轨道六根数和着陆器的几何构形有关。结合式(15)的主对角线元素,可得着陆器频率稳定度对定位精度的影响如式(19)~(21):
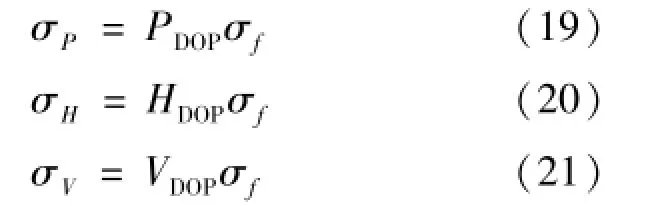
其中σP是空间位置定位标准差,σH是水平定位标准差,σV是垂直定位标准差。由上式可看出要提高着陆器的定位精度,一方面要选择合适的轨道器和着陆器之间的几何构形,以降低定位精度因子;另一方面要提高轨道器的频率稳定度以降低多普勒频率测量标准差。在轨道器发射载频已知的条件下,在整个观测时间段内,着陆器多普勒频率测量标准差σf和着陆器时钟的频率稳定度[15]有式(22)所示对应关系[16]:

上式中ζ表示观测时间τ内的频率稳定度。
5 仿真分析
STK中对着陆器和地月L2轨道中继星进行建模,将中继星的星历导出为月固坐标系下的三维位置和速度。针对不同的仿真条件,以不同的采样间隔得到三个时刻的卫星星历。将第二个星历数据转换为月球地理坐标系[13],将其星下点作为原点,对其周围经度和纬度在[-1.5°,1.5°]的区域进行离散化,并将其转为月固坐标系下的点计算DOP值。月球半径约为1 734.4 km,选取经纬度范围[-1.5°,1.5°]对应经度和纬度方向的[-45.48 km,45.48 km]的区域,着陆器位于该区域时与中继星距离较近,便于中继星的天线主波束进行照射。
仿真1:载频2 GHz,对应S频段。轨道器高度100 km、倾角90°,着陆器以10 s的采样间隔获得3个多普勒测量值,天线架高5 m,着陆器定位的DOP值如图4所示。轨道器三个位置采样的星下点也一并给出,在图中以洋红色的原点表示。
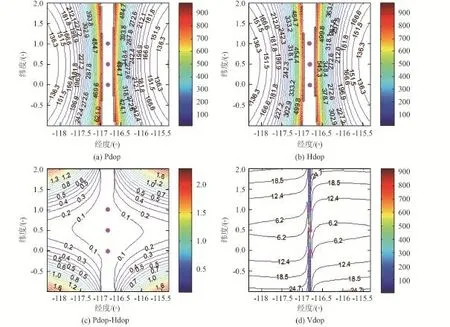
图4 仿真1的DOP值分布Fig.4 DOP in Simulation 1
图4(c)是PDOP减去HDOP后的差值。由图4可看出,在轨道器星下点附近的区域内,着陆器定位的PDOP、HDOP、VDOP值较大,这些区域为定位盲区。DOP值以轨道器在月面上的投影为中心对称分布,其中PDOP和HDOP沿着星下点轨迹的两侧逐渐减小。除了轨道器运行星下点的区域外,VDOP在定位区域内的变化不大,且比PDOP和 HDOP小一个数量级。定位区域内的PDOP主要由HDOP决定。根据式(19)和式(22),在图4中PDOP在小于1000的区域内,若σf<0.01 Hz,则理论上可获得优于10 m的定位精度,此时要求着陆器时钟在30s内频率稳定度优于5×10-12(τ=30 s)。
仿真2:载频8 GHz,对应X频段。其他仿真参数保持与仿真1一致,着陆器定位的DOP值如图5所示。
从图5可看出,适当提高载频可降低DOP,改善定位精度。图5中PDOP在小于100的区域内,若σf<0.1 Hz,则理论上可获得优于10 m的定位精度,此时要求着陆器在30 s内频率稳定度优于1.25×10-11(τ=30 s)。
仿真3:载频27 GHz,其对应Ka频段。着陆器测量地月L2轨道中继星的上行信号。以6 h的采样间隔得到3个多普勒稀疏采样测量值,天线架高5 m。以第二个采样数据的星下点作为原点,对其周围经度和纬度在[-2.5°,2.5°]的区域进行离散化,并将其转为月固坐标系下的点计算DOP值,着陆器定位的DOP值如图6所示。
从图6可看出,采用地月L2轨道中继星对着陆器的月面多普勒定位中,定位区域内的PDOP由HDOP和VDOP共同决定,且VDOP小HDOP一个数量级。在整个定位区域内,DOP值的分布较平缓,且星下点附近无不可定位的区域。这是由于地月L2轨道中继星运动速度较慢,着陆器与L2中继星之间的几何构形较小所导致。图6中PDOP值在30 600到31 100之间。若σf<0.001 Hz,则理论上可获得优于100 m的定位精度,此时要求着陆器的时钟在18h内频率稳定度优于3.7×10-14(τ=18 h)。
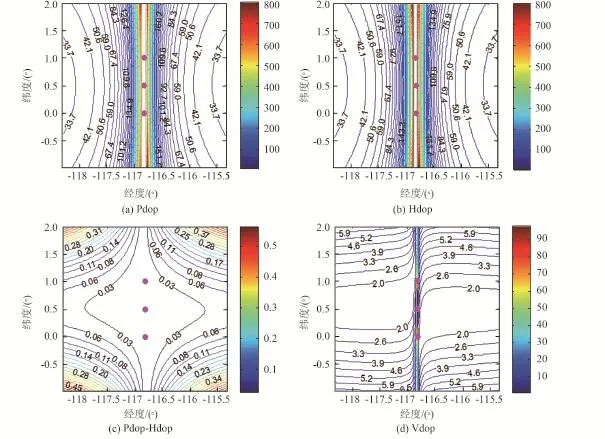
图5 仿真2的DOP值分布Fig.5 DOP in simulation 2
6 结论
1)本文讨论地月L2中继星或月球轨道器对月球背面着陆器多普勒定位,可用于由于月球的遮挡无法用地面跟踪站对其进行月面导航定位的情况下,实现对着陆器的月面导航定位。
2)月球轨道器对着陆器多普勒定位时,星下点沿轨道器运动方向的区域内DOP值较大,存在定位盲区。着陆器位于轨道器星下点两侧的区域时,定位精度较高。
3)提高上行播发信号的载频可提高多普勒定位精度。稀疏多普勒采样点之间的多普勒变化越快,越利于提高定位精度。
4)当着陆器不在轨道器的定位盲区内时,要得到优于10 m的定位精度,使用500 MHz载频需要着陆器时钟频率稳定度优于 2×10-12(τ=30 s);使用2 GHz载频需要着陆器时钟频率稳定度优于5×10-12(τ=30 s)。
5)地月L2轨道中继星对着陆器多普勒定位时,整个定位区域不存在定位盲区,但 PDOP较大,需要较高的载频、较长的观测时间间隔、较高的时钟稳定度才可实现定位。要达到优于100 m的月面定位精度,在12 GHz的载频下,需要着陆器时钟频率稳定度优于8.3×10-14(τ=18 h)。
6)着陆器的多普勒定位模式中,采用环月轨道器的模式可实现较高的定位精度,但可定位范围较小;采用地月L2轨道中继星模式的定位精度较差,但可定位范围广。
7)本文假设载频等于标称值,实际中载频随着时间的变化与标称值存在误差,载频误差对定位精度的影响有待以后的深入研究。
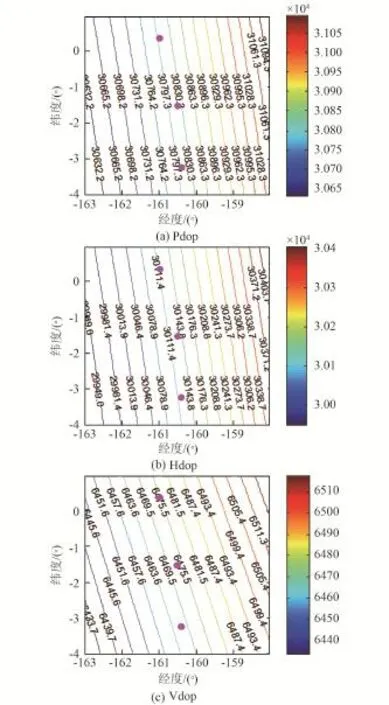
图6 仿真3的DOP值分布Fig.6 DOP in simulation 3
(
)
[1]Wu K C,Antol J,Watson J J,et al.Lunar lander structural design studies at NASA Langley[C]//AIAA SPACE 2007 Conference&Exposition.2007:6137.
[2]Benjamin D,Curtis M.Lunar lander concepts for human ex⁃ploration[J].Journal of Spacecraft and Rockets,2006,45(2):383⁃393.
[3]陈金宝,聂宏,陈传志,等.载人登月舱设计及若干关键技术研究[J].宇航学报,2014,35(2):125⁃136.Chen Jinbao,Nie Hong,Chen Chuanzhi,et al.Design and key techniques for lunar lander system of manned lunar land⁃ing[J].Journal of Astronautics,2014,35(2):125⁃136.(in Chinese)
[4]昌胜骐,黄勇,刘庆会,等.利用搜索法对嫦娥三号着陆器和巡视器定位[J].宇航学报,2015,36(6):624⁃629.Chang Shengqi,Huang Yong,Liu Qinghui,et al.Positioning of Chang′e⁃3 Lander and Rover Based on Search Method[J].Journal of Astronautics,2015,36(6):624⁃629.(in Chi⁃nese)
[5]SCAWG.NASA space communication and navigation archi⁃ tecture recommendations for 2005⁃2030[R].NASA,Space Communication Architecture Working Group,2006.
[6]刘磊.月球中继通信与导航技术研究进展和建议[J].国际太空,2014(4):51⁃54.Liu Lei.Research progress and suggestion for lunar relay com⁃munication and Navigation[J].Space International,2014(4):51⁃54.(in Chinese)
[7]陈义,程言.天文导航的发展历史、现状及前景[J].中国水运,2006,4(6):27⁃28.Chen Yi,Cheng Yan.Celestial navigation development histo⁃ry,present situation and prospect[J].China Water Trans⁃port,2006,4(6):27⁃28.(in Chinese)
[8]赵书阁,张景瑞,张尧.日地系统L2点Halo轨道自主天文导航及精度分析[J].北京理工大学学报,2013,33(11):1119⁃1139.Zhao Shuge,Zhang Jingrui,Zhang Yao.autonomous celestial navigation and analysis of precision for spacecraft on Halo or⁃bit near L2 point of Sun⁃Earth system[J].Transactions of Beijing Institute of Technology,2013,33(11):1119⁃1139.(in Chinese)
[9]张天光,王秀萍,王丽霞,等.捷联惯性导航技术[M].北京:国防工业出版社,2007:5⁃26.Zhang Tianguang,Wang Xiuping,Wang Lixia,et al.Strap⁃down Inertial Navigation Technology[M].Beijing:National Defense Industry Press,2007:5⁃26.(in Chinese)
[10]李茂登.月球软着陆自主导航、制导与控制问题研究[D].哈尔滨:哈尔滨工业大学,2011.Li Maodeng.Study the Guidance,Autonomous Navigation and Control of Lunar Soft Landing[D].Harbin:Harbin Insti⁃tute of Technology,2011.(in Chinese)
[11]陈阳.小行星探测器着陆段自主光学导航方法研究[D].哈尔滨:哈尔滨工业大学,2013.Chen Yang.Research on Autonomous Optical Navigation Scheme in Asteroid Probe[D].Harbin:Harbin Institute of Technology,2013.(in Chinese)
[12]杜兰,张中凯,于亮,等.圆型限制性三体问题下Halo绕月轨道的星间测距定轨[J].测绘学报,2013,42(2):184⁃190.Du Lan,Zhang Zhongkai,Yu Liang,et al.SST orbit deter⁃mination of Halo⁃LMO constellation in CRTBP[J].Acta Geo⁃daetica et Cartographica Sinica,2013,42(2):184⁃190.(in Chinese)
[13]中华人民共和国国家标准:中国科学院国家天文台.GB/T 30112⁃2013月球空间坐标系[S].北京:中国标准出版社,2014.P.R.C.National Standard:Chinese Academy of Sciences,National Astronomical Observatories GB/T 30112⁃2013 The Lunar Coordinate System[S].Beijing:China Standard Press,2014。(in Chinese)
[14]谢刚.GPS原理与接收机设计[M].北京:电子工业出版社,2009:110⁃120.Xie Gang.Principles of GPS and Receiver Design[M].Bei⁃jing:Publishing House of Electronics Industry,2009:110⁃120.(in Chinese)
[15]雷雨.GPS星载原子钟频率稳定度分析[C]//2011全国时间频率学术会议,2011:435⁃439.Lei Yu.GPS atomic clock frequency stability analyses[C]//2011 China Time and Frequency Symposium,2011:435⁃439.(in Chinese)
[16]Rutman J,Walls F L.Characterization of frequency stability in precision frequency sources[J].Proceedings of the IEEE,1991,79(7):952-960.
Precision Analysis of Doppler Positioning for Lunar Lander onFar Side of Moon Using Earth⁃Moon L2 Relay Satellite or Lunar Orbiter
LEI Wenying1,MENG Yansong1,LEI Wenhua2,BIAN Lang1,WANG Ying1
(1.China Academy of Space Technology(Xi'an),Xi'an 710100,China;2.School of Sciences,Tibet University,Lhasa 850000,China)
To overcome the drawback that the ground station on the earth could not position the lunar lander on the far side of the moon,two solutions were investigated.One solution is to position the lu⁃nar lander by measuring the Doppler frequency of downlink signal transmitted by the lunar orbiter and the other is by measuring the Doppler frequency of the signal from an earth⁃moon L2 relay satellite.In the lunar fixed coordinate system,the Doppler positioning precisions of the two solutions were analyzed respectively for the lunar lander.The influences of the dilution of precision and frequency stability on the positioning precision were analyzed.These two Doppler lunar lander positioning scenarios were modeled in STK(Satellite Tool Kit),and the exported ephemerides were used to evaluate the positio⁃ning precision quantitatively.Meanwhile,the time constraints and spatial constraints of the two solu⁃tions were discussed.The frequency stability requirements for the clock of the lunar lander were given quantitatively with respect to different carrier frequencies and different observing time.
Earth⁃Moon L2 point;lunar orbiter;lunar lander;Doppler positioning;precision analy⁃sis
V448
A
1674⁃5825(2016)06⁃0774⁃07
2016⁃05⁃12;
2016⁃11⁃09
国家自然科学基金(91438107)
雷文英(1985-),男,博士,工程师,研究方向为导航信号处理和定位跟踪技术。E⁃mail:lordleid@163.com

