航天器核动力推进系统热力学性能研究
冯致远,张昊春∗,吉 宇,程献伟,赵广播
(1.哈尔滨工业大学能源科学与工程学院,哈尔滨150001;2.清华大学核能与新能源技术研究院,北京100084)
航天器核动力推进系统热力学性能研究
冯致远1,张昊春1∗,吉 宇2,程献伟1,赵广播1
(1.哈尔滨工业大学能源科学与工程学院,哈尔滨150001;2.清华大学核能与新能源技术研究院,北京100084)
作为未来航天能源重要候选的以CO2为工质的布雷顿循环空间核动力系统,目前在热力循环分析的研究方面有待深入。以钠冷快堆超临界CO2布雷顿循环作为分析对象,针对不同工质最高循环温度下的循环效率以及不同的增压比和低温回热器冷端温差对循环效率的影响进行了研究。通过建立CO2实际气体的RK方程和焓表达式,得出了输出功率随增压比的变化规律。研究结果表明提高循环最高温度和增压比均能有效提升循环效率,但提高增压比将影响回热器的回热效果,而较低的增压比会使高温回热器热负荷显著增加,合适增压比范围为3.0~3.2。
闭式布雷顿循环;超临界CO2;RK方程;增压比
1 引言
随着深空探测的不断发展,空间核动力逐渐应用于深空探测器中。相比太阳能推进,空间核动力探测器极端环境运行稳定性更好,输出功率高,能量密度大,工作时间长,并且不依赖于太阳能,探测区域更广[1]。空间核反应堆电源有静态转换和动态转换两种方式。动态转换方式中,在兆瓦级功率阶段,布雷顿循环是最佳选择[1],一般与液态金属冷却快堆、热管式液态金属冷却反应堆、高温气冷堆进行系统组合[2]。空间布雷顿循环转换器是燃气轮机闭式循环模型,工质为惰性气体[3]。
虽然早在上世纪60年代,美国和苏联已将核动力用于飞船推进,但对于能量转换系统的深入分析在近期才逐渐发展完善[1],而选择良好的循环系统及参数可以增大输出功率,提高效率,减轻飞行器质量。因此对于近期地月载人航天研究及后续的火星深空探测,引入空间核动力推进的概念并对能量转换系统进行分析具有重要意义。
目前,布雷顿循环得到了广泛而深入的研究。Le Roux等人基于热力学第二定律和最小熵产概念,对太阳能布雷顿循环建立了模型分析,为优化计算提供了理论依据[4]。Robin Rocco等人分析了气冷堆型的闭式布雷顿循环模型并验证了模型的合理性,计算结果表明,增大散热器可以提高散热效率,但会增加反应堆功率输入[5]。Jason Tar⁃lecki等人讨论了外太空环境下不同工质的循环,分析表明在布雷顿循环中双原子气体的循环特性要高于单原子[6]。
相对于氦气,超临界CO2(S⁃CO2)具有高比热容,高密度的特性,反应堆模型设计更为紧凑,同时较低的透平进口温度降低了材料的耐热性要求[7]。本文在文献[8]的基础上,主要对超临界CO2布雷顿循环与钠冷快堆的组合式模型进行热力学分析。通过构建带有低温回热器(LTR)和高温回热器(HTR)以及分流压缩的布雷顿循环模型,建立了完整的系统数值计算程序,进一步研究了在773K最高循环温度下,循环效率随增压比的变化趋势,增加了对回热器及输出功率的研究,为循环的合理设计提供了参考数据及设计方向。
2 布雷顿循环热力学模型
对于再压缩S⁃CO2布雷顿循环系统,由于S⁃CO2在临界点附近有很大的比热变化,为了避免进气口出现逆温差,设置有两个压缩机(如图1中的Comp#1及Comp#2)。同时,采用分流可以减小回热器热端流体间温差,提高进入堆芯的换热温度[9]。这里引入参数x表示流量份额,即进行预冷的流量所占比例,合理的比例为0.68~0.72[7]。从图1中可以看出,工质气体在汽轮机做功,经高低温回热器换热后发生分流,一部分经过预冷后进入1号压气机(Comp#1)压缩,另一部分直接进入2号压气机(Comp#2)压缩,1号压气机出口工质在低温回热器中回热后与2号压气机出口气体汇合,共同经高温回热器后通过在反应堆热源吸热,成为高温高压气体再次进入汽轮机做功(图中标识为Turbine)完成循环。
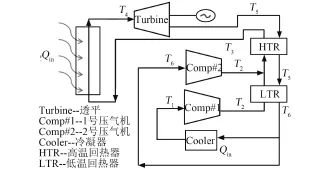
图1 再压缩S⁃CO2布雷顿循环系统Fig.1 Recompression S⁃CO2Brayton cycle system
2.1 S⁃CO2状态方程及焓表达式的建立
2.1.1 状态方程
由于在几种实际气体状态方程中,在超临界状态下RK方程拟合较好,SRK及PR方程误差较大,EXP⁃RK及PR⁃EXP方程误差很小,但方程形式较RK方程复杂很多[10]。因此分析所用状态方程仍沿用式(1)所示文献[8]中RK方程:
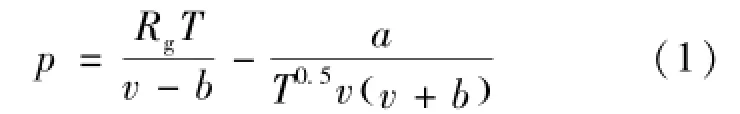
2.1.2 焓表达式的推导
循环效率的推导需要用到循环各点的焓值,因此需要建立焓的表达式。焓的一般微分关系式可以表示为式(2)[11]:

对式(2)的求解按先定压后定温压缩过程积分,并改变积分变量p为v,由文献[8]推导过程可得焓的积分表达式如式(3):

为了简化结果,引入余函数,余焓[12],即理想焓值与实际焓值的差值,因此得实际气体焓和余焓的表达式如式(4)、(5):
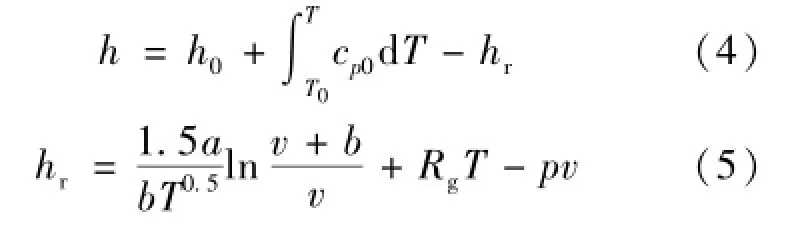
式中a、b参数即前节所述状态方程中参数,积分下限T0为273.15℃。
2.2 循环各部分的关系式及循环效率
在两个压气机中,气体的增压比π相同,为了简化分析,假设工质气体在其中进行绝热压缩,因此满足热力学第一定律如式(6):
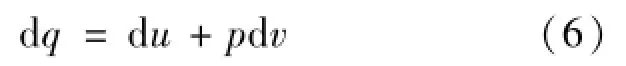
式(7)所示为热力学能一般关系式[11]:
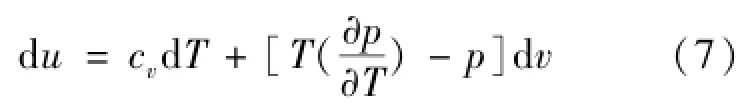
式中cv为定压比热容,代入式(6)得式(8):
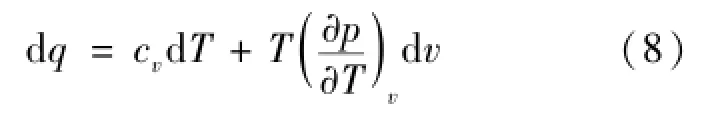
由文献[13]可得定容比热容表达式如式(9):
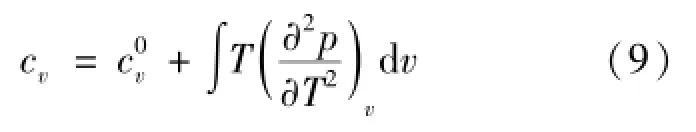
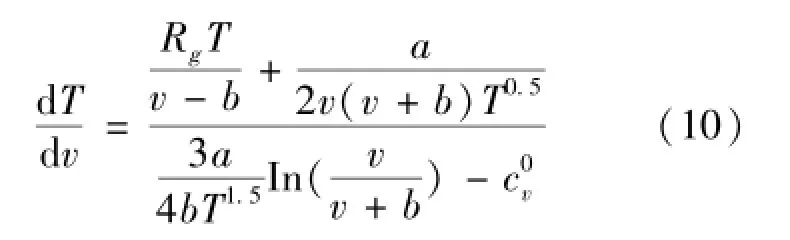
式(10)即RK实际气体准静态绝热过程方程。在透平中,依然假定工质进行绝热膨胀过程,气体降压比依然为相同数值的π。计算程序与压气机原理相同。
在回热器中,工质进行热量交换,进行预冷的CO2分流比为x时,在低温回热器中满足式(11):
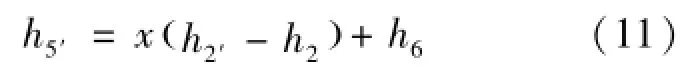
在高温回热器中满足式(12):
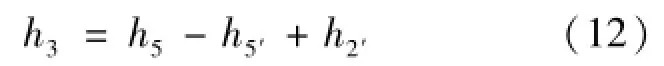
因此循环的热效率为式(13):

2.3 布雷顿循环模型的验证
在建立了完整的布雷顿循环热力学模型后,其合理性需要检验。对于焓表达式的合理性可以通过文献[10]数据证明。
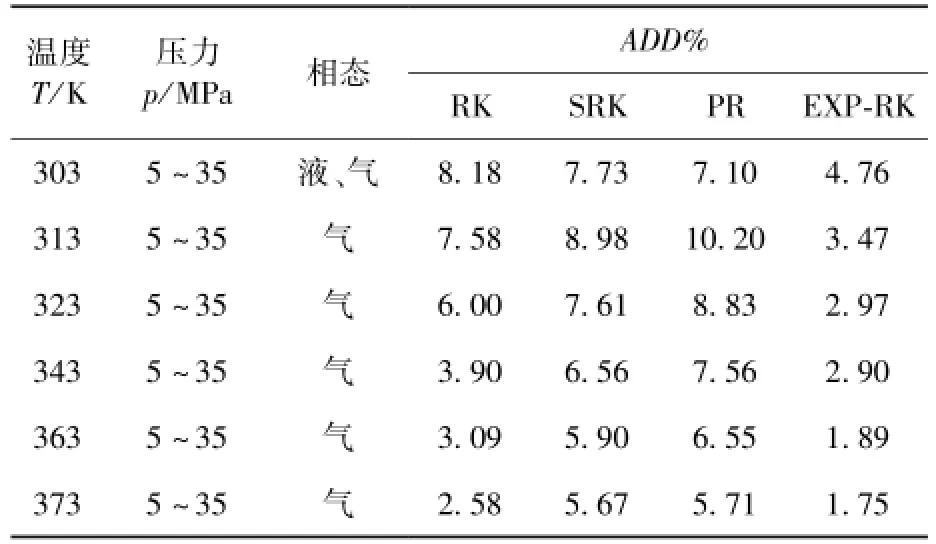
表1 不同状态方程CO2密度预测结果Table 1 The prediction results of density of CO2based on different state equation
由表1可知RK方程在临界条件下误差为8%,随着温度的升高误差逐渐减小,结合所研究系统数据,RK方程在计算2号压气机,透平和回热器的参数时误差均不会超过3%,因而所得结果合理。
进一步需要检验的是在准静态绝热过程方程(10)的基础上建立的系统计算模型。检验算例使用文献[7]数据,对比结果在表2中列出。
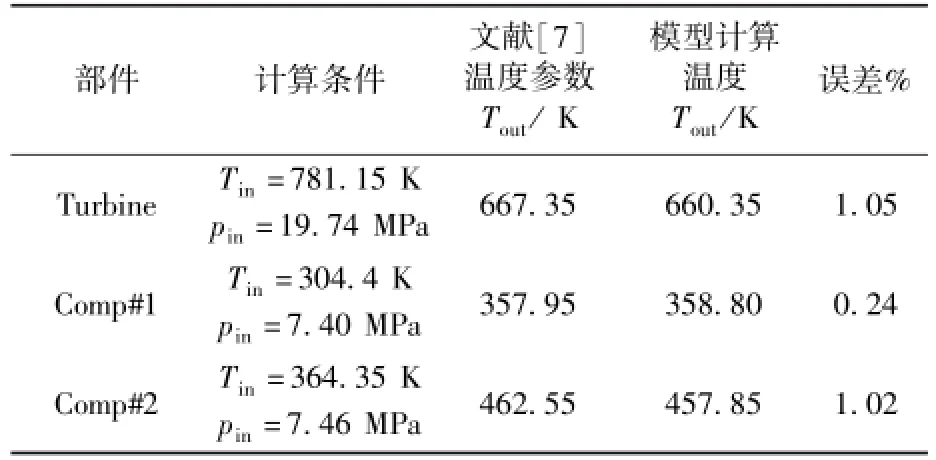
表2 系统模型可靠性检验Table 2 The test of reliability of system model
从表2可以看出所建立的模型在上述算例中具有良好的精确性和可靠性。透平,1号压气机,2号压气机的出口温度与文献标准值误差分别为:1.05%,0.24%,1.02%,均与参考文献值相差很小,因此系统模型之后的计算结果可靠。
3 不同工况下的计算
由已建立模型可知,循环效率由循环最高温度、增压比、低温回热器冷端温差及初始工况等因素决定。根据相关文献[3],初始工况设定为:p1=7.40 MPa,T1=304.4 K,通过状态方程及焓表达式依次求得比体积ν1=0.0027 m3/kg,焓值h1=-104.88 kJ/kg;设定流量份额x为0.71;循环最高温度分析873 K、823 K、773 K、723 K四种情况;低温回热器温差设定为10 K、15 K、20 K、25 K四种情况。为研究循环效率随增压比的变化趋势,将773 K时的增压比范围扩大为1.8~3.8。在文献[8]的基础上,进一步研究不同增压比对回热器冷端温差及热负荷的影响,以证明过高增压比的不可行性。最后通过分析773 K时输出功率随增压比的变化对循环参数设定进行综合分析。
3.1 循环效率与低温回热器冷端温差及增压比的关系
对于最高循环温度为773 K,分流比 x为0.71的情况,增压比π设定为2.2~3.0。表3、4仅列出3.0,2.8的循环工况数据,其余数据参见文献[7]。表中第一行列出主要参数及单位,第二行为10 K、15 K、20 K、25 K四个不同低温回热器冷端温差。左侧一列为循环部件,右侧为其不同温差下的对应参数值,其中1、2号压气机、汽轮机均列出了进出口p、v、T、h等参数,in为进口参数,out为出口参数。低温回热器(LTR)列出了低压侧入口参数p、h,高温回热器(HTR)列出了高压侧出口参数p,h。

表3 增压比为3.0的工况数据Table 3 The data under pressure ratio 3.0
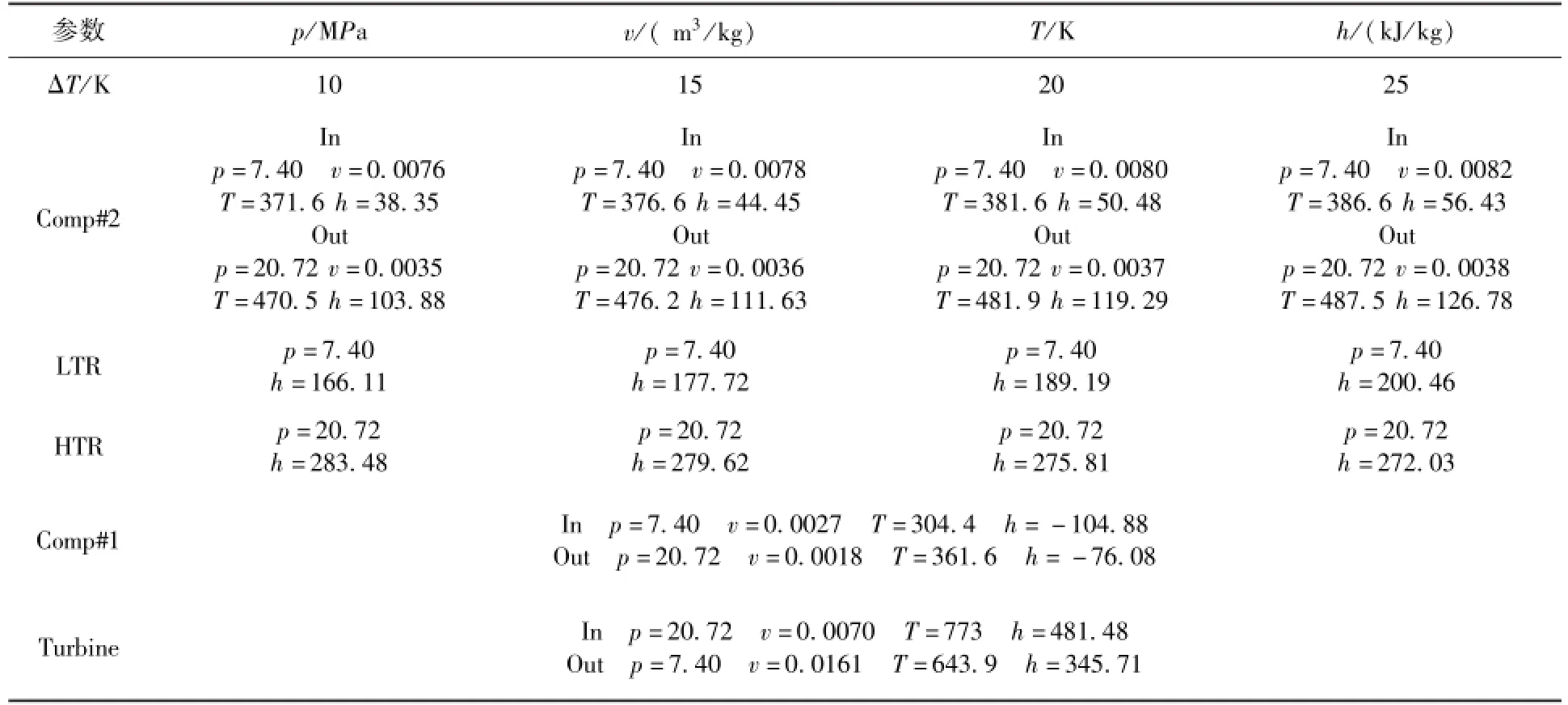
表4 增压比为2.8的工况数据Table 4 The data under pressure ratio 2.8

表5 增压比为3.0的工况数据Table 5 The data under pressure ratio 3.0

表6 增压比为2.8的工况数据Table 6 The data under pressure ratio 2.8
通过比较增压比2.2~3.0的数据可以看出,由于ΔT的增加,2号压气机进出口焓均提高,从而LTR换热量显著增加,而回热过程总换热量却减少,所以可以看出HTR的传热情况随ΔT增加而恶化。
3.2 循环效率与最高温度及增压比的关系
在此工况下,仅汽轮机及HTR部分参数改变,其余参数与前一部分各表ΔT=10 K的参数相同。表5、表6仅列出增压比为3.0、2.8时的透平参数与 HTR高压侧出口参数,增压比为2.6、2.7的数据见文献[8]。表中3、4行右侧为部件对应参数值,汽轮机给出了进出口参数p、v、T、h,in表示进口参数,out表示出口参数。HTR给出了高压侧出口参数。
从增压比2.6~3.0的数据可以看出,提高循环最高温度可以改善回热器传热,从而使最佳增压比提高。同时相同增压比下,HTR的高压侧出口焓显著增大,但在热源的吸热量也在增加,且温度每升高50 K,单位质量吸热量增加10 kJ左右。
3.3 输出功率与增压比的关系
循环效率及输出功率均是判断循环性能的重要指标,因此,在研究循环效率的数据基础上,应当通过输出功率的分析进行验证。为简化分析,假定核动力飞船稳定运行,所需推力恒定,因而循环系统输出功率恒定,循环系统处于稳态,即输出功率仅与循环净比功 w(kJ/kg)和质量流量 M(kg/s)有关,因此可得式(14)、(15):
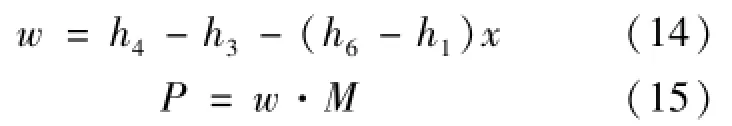
[2],设定质量流量为5 kg/s,对应的研究工况为循环最高温度773 K,LTR冷端温差为10 K。
3.4 余热排出及辐射散热器
布雷顿循环系统的参数设计还会影响到余热排出系统,即辐射散热器的设计。从系统模型可以看出低温回热器冷端温度与散热器面积有关。根据式(16)所示斯蒂芬⁃玻尔兹曼定律:
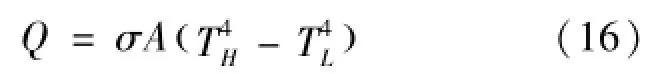
式中,A为散热器面积,TH为低温回热器冷端低压侧温度T6,TL为宇宙背景辐射温度3 K,Q为余热排出量,即工质在冷凝器中的热量交换,通过式(17)计算:
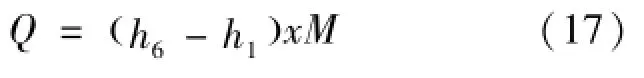
4 计算结果与分析
从第三章的计算数据可以得出循环效率在不同最高温度下随增压比的变化情况及在不同低温回热器冷端温度下随增压比的变化情况。结果如表7及图2所示:
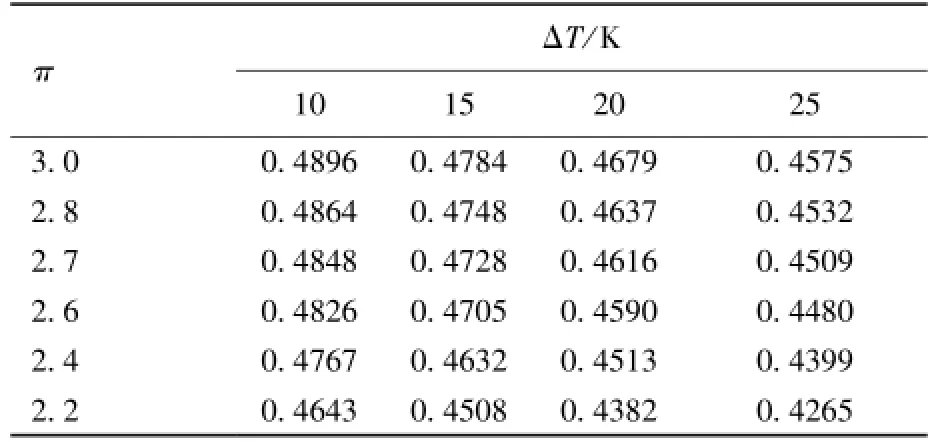
表7 增压比及冷端温差对循环效率的影响Table 7 The effect of pressure ratio and temperature difference of cooler⁃side of LHR on cycle effi⁃ciency

图2 低温回热器冷端对循环效率的影响Fig.2 Effect of cooler⁃side of LHR on cycle efficiency
从表7和图2中可以看出,在循环最高温度固定为773 K,流量份额x为0.71的情况下,四个ΔT曲线循环效率均随增压比的增大而升高,但趋势渐缓。同时可以看出ΔT越大,循环效率越低,并且LTR冷端温差对循环效率影响较大,因为ΔT越大,回热过程总换热量减少,导致吸热量增加,效率降低。
表8和图3给出了增压比及最高循环温度对循环效率的影响。

表8 增压比及最高循环温度对循环效率的影响Table 8 The effect of pressure ratio and highest cycle temperature on cycle efficiency

图3 最高温度对循环效率的影响Fig.3 The effect of highest cycle temperature on cy⁃cle efficiency
从图3及表8可以看出,循环效率随最高温度的提高大幅增长,在所选增压比范围中,循环效率均不断增加,但提高幅度不大且近似线性。为了进一步研究增压比对循环效率的影响趋势及回热器的传热影响,同时考虑到温度过高可能引起CO2与燃料元件反应,取较保守最高温度773 K,冷端温差10 K作为研究工况,增压比范围扩大为1.8~3.8,计算结果如图4~6所示。
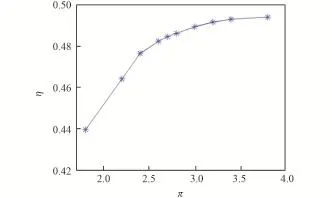
图4 增压比对循环效率的影响Fig.4 The effect of pressure ratio on cycle efficiency
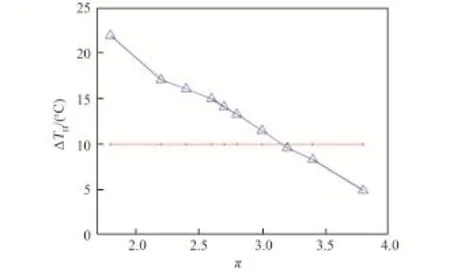
图5 增压比对HTR冷端温差影响Fig.5 The effect of pressure ratio on temperature difference of cooler⁃side of HTR
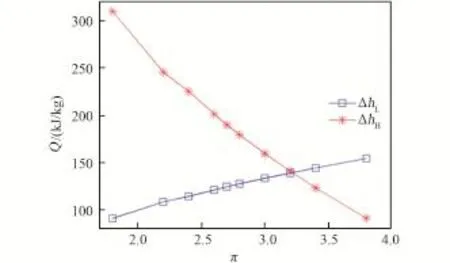
图6 增压比对HTR,LTR的传热量影响Fig.6 The effect of pressure ratio on heat transfer of HTR,LTR
由图4可知,随着增压比的增大,循环效率的增幅迅速降低,在3.4后趋于平缓。而对于换热器HTR、LTR冷端温差均需要在10 K以上,但由图5可知HTR冷端温差(也是LTR热端温差),随着增压比增大,其值近似线性降低,当π=3.2时,温差为9.6 K,低于10 K。同时由图6可知,当增压比较小时,HTR热负荷大,当增压比增大时,LTR热负荷较大。因此合适的增压比为2.8~3.2。通过对应的输出功率计算如图7所示。

图7 输出功率随增压比的变化Fig.7 Output power varies with pressure ratio
由图7可知,在增压比研究范围内,输出功率随增压比大幅增大,且增幅渐缓,但相比较循环效率,在π=3.4时仍具有较高的增长速度。因此综合循环效率及输出功率,最适合的增压比为3.0~3.2。为了更好地提高循环特性,应当研发新型材料,提高工质循环的最高温度。
热力循环系统还会影响辐射散热器的面积,从而影响飞船的重量及结构复杂性。由第三节所建系统模型可以看出散热器的面积仅与循环的增压比和低温回热器冷端温差有关,与循环最高温度无关,计算结果在图8、图9给出。
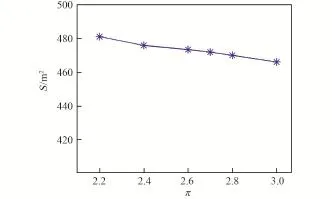
图8 散热器面积随增压比的变化Fig.8 Radiator area varies with pressure ratio
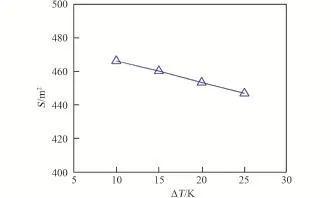
图9 散热器面积随冷端温差的变化Fig.9 Radiator area varies with temperature differ⁃ence of cooler⁃side of LTR
从图8,图9可以看出提高增压比,增大温差均可以减小辐射散热器的面积,且近似为线性关系。但在研究范围内对面积的影响并不明显。
以上计算分析缩小了工况的优化分析范围,在小范围中,部分变量可近似为常量处理,从而简化进一步的优化。深入分析可以基于热力学第二定律考虑压气机绝热效率及汽轮机绝热效率,以及工质在流动过程的压损、功损等。并引入熵和有用功的概念,对各部件运用最小熵产理论(EGM)[4]进行分析计算,得出更加精确科学的最适条件。
超临界CO2布雷顿循环具有循环效率高,输出功率大的优点。但通过分析可以看出余热排出量很大,因此辐射散热器的结构会较为复杂,并增加系统的总重量。尤其在设计兆瓦级布雷顿循环飞船时,其散热器面积会达1000 m2,影响系统的性能。因此研究良好的散热系统及余热的利用对飞船系统设计也是至关重要的。
5 结论
本文通过构建超临界CO2的计算模型,对组合式钠冷快堆超临界CO2布雷顿循环进行了分析,得出的结论可归纳为以下三点:
1)低温回热器冷端温差是影响循环效率的重要因素。在不影响LTR换热的情况下,较低的冷端温差可以增加换热器总换热量。
2)提高循环最高温度可以大幅提升循环效率,并且提高循环最高温度可以增大HTR的换热温差,从而使换热量显著提升,从而弥补提高增压比造成的回热器传热恶化。
3)增压比也是影响因素之一,增大增压比可以提高循环效率,但过高的增压比会使回热器内出现夹点,造成回热效果变差甚至无法正常换热。在设定最高温度773 K,低温回热器冷端温差10 K并综合考虑循环效率及输出功率的条件下,增压比的合适范围为3.0~3.2。
参考文献(References)
[1]Buden D.Space Nuclear Fission Electric Power Systems[M].Polaris Books,2011:3⁃9.
[2]Otting W,Determan W,Frye P,et al.Brayton power conver⁃sion system technology development[J/OL].https://engi⁃neering.purdue.edu/Engr,2003.
[3]Mason L S.Dynamic energy conversion:vital technology for space nuclear power[J].Journal of Aerospace Engineering,2013,26(2):352⁃360.
[4]Le Roux W G,Bello⁃Ochende T,Meyer J P.A review on the thermodynamic optimisation and modelling of the solar thermal Brayton cycle[J].Renewable and Sustainable Energy Re⁃views,2013,28:677⁃690.
[5]Amin M R,Rocco R.Dynamic modeling of a closed loop Brayton cycle for space auxiliary electric power systems[C]//3rd BSME⁃ASME International Conference of Thermal Engi⁃ neering.Dhaka,Bangladesh,December 20⁃22,2006.
[6]Tarlecki J,Lior N,Zhang N.Evaluation of some thermal power cycles for use in space[C]//Proc.ECOS 2006,Ju⁃ly12⁃14,Crete,Greece,2006.
[7]Cha J E,Lee T H,Eoh J H,et al.Development of a super⁃critical CO2Brayton energy conversion system coupled with a sodium cooled fast reactor[J].Nuclear Engineering and Technology,2009,41(8):1025⁃1044.
[8]冯致远,张昊春,吉宇.钠冷堆超临界CO2布雷顿循环特性研究[C]∥工程热力学与能源利用⁃2015年中国工程热物理学会年会论文集.厦门:工程热物理学报,2015.Feng Zhiyuan,Zhang Haochun,Ji Yu.Research of properties of super critical CO2Brayton cycle coupled with sodium cooled fast reactor[C]//Xiamen:Thermodynamic and Energy Utilize China Thermal Physics Proceedings,2015.(in Chinese)
[9]段承杰,王捷,杨小勇.反应堆超临界CO2Brayton循环分析[J].原子能科学技术,2010,44(11):1341⁃1348.Duan Chenjie,Wang Jie,Yang Xiaoyong.Analyzation of su⁃per critical CO2Brayton cycle reactor[J].Atomic Energy Sci⁃ence and Technology,2010,44(11):1341⁃1348.(in Chi⁃nese)
[10]王庆,吴晓东.气、液、超临界CO2相态及物性计算模型研究[J].中国石油大学胜利学院学报,2012,26(2):11⁃13.Wang Qin,Wu Xiaodong.Study of physical calculation model and phase of gas,liquid and super critical CO2[J].Journal of Shengli College China University of Petroleum,2012,26(2):11⁃13.(in Chines)
[11]严家騄,王永青.工程热力学[M].北京:中国电力出版社,2014:151⁃170.Yan Jialu,Wang Yongqing.Thermodynamic Engineering[M].Beijing:China Electric Power Press,2014:151⁃170.(in Chinese)
[12]刘志刚,刘咸定,赵冠春.工质热物理性质计算程序的编制及应用[M].北京:科学出版社,1992:147⁃182.Liu Zhigang,Liu Xianding,Zhao Guanchun.Edition and Application of Calculation Program of Working Fluids Thermal Physics Properties[M].Beijing:Beijing Science Press,1992:147⁃182.(in Chinese)
[13]郑世燕,杨惠山.推广的Redlich⁃Kwong实际气体绝热过程[J].泉州师范学院学报,2012,30(2):19⁃20.Zheng Shiyan,Yang Huishan.Generalized Redlich⁃Kwong real gas adiabatic process[J].Journal of Quanzhou Normal University,2012,30(2):19⁃20.(in Chinese)
Study on Thermodynamic Performance of Nuclear Power Propulsion System in Spacecraft
FENG Zhiyuan1,ZHANG Haochun1∗,JI Yu2,CHENG Xianwei1,ZHAO Guangbo1
(1.School of Energy Science and Engineering Harbin Institute of Technology,Harbin 150001,China;2.Institute of Nuclear and New Energy Technology Tsinghua University,Beijing 100084,China)
As a promising proposal for the future space exploration,Brayton cycle space nuclear power system,which uses super critical CO2as the working fluid,is still lack of the thermodynamic analysis up to now.Therefore,the super⁃critical CO2 Brayton cycle with sodium cooled fast reactor was studied.The effects of the highest temperature in cycle,the pressure ratio and the temperature difference of the cooler⁃side of low temperature recuperator(LTR)on cycle efficiency were dis⁃cussed.The law of output power varying with the pressure ratio was obtained by building the expres⁃sion of CO2 real gas enthalpy and RK equation during the analysis process.The study results showed that the cycle efficiency could increase effectively by improving the highest cycle temperature or pressure ratio.But,the heat transfer condition deteriorated with the raised pressure ratio.While low pressure ratio could lead to high heat load of the high temperature recuperator.Thus,the suitable scope of pressure ratio is 3.0~3.2.
closed Brayton cycle;super⁃critical CO2;RK equation;pressure ratio
V439+.5
A
1674⁃5825(2016)06⁃0797⁃08
2016⁃05⁃30;
2016⁃11⁃14
国家自然科学基金委创新研究群体(51421063);国家自然科学基金(51536001)
冯致远(1995-),男,硕士研究生,研究方向为空间核能动力、核能系统。E⁃mail:1070483968@qq.com
∗通讯作者:张昊春(1977-),男,博士,副教授,研究方向为飞行器热控、目标特性、军用能源技术。E⁃mail:zhc5@vip.163.com

