一种改进的共形阵方向图综合方法*
夏 欢 张兴敢 柏业超
(南京大学电子科学与工程学院,南京,210023)
一种改进的共形阵方向图综合方法*
夏 欢 张兴敢 柏业超
(南京大学电子科学与工程学院,南京,210023)
与传统阵列相比,共形阵安置更为灵活,应用更为广泛。然而,针对共形阵的方向图综合也更为复杂。传统的方向图综合方法对共形阵并不适用。通过在旁瓣区域施加虚拟干扰能够有效实现共形阵的方向图综合。如何通过迭代过程控制虚拟干扰功率的大小成为该方法的关键。现有的迭代方法一般存在收敛缓慢或计算复杂的问题。本文基于线性约束最小方差准则,提出了一种改进的共形阵方向图综合方法。该方法适用于任意阵型的方向图综合。仿真实验证明,该方法能加快收敛速度,并降低自适应波束形成器对迭代系数的依赖性。
共形阵;方向图综合;虚拟干扰;线性约束最小方差
引 言
与传统阵列相比,共形阵具有与载体共形的突出优点,在机载、星载等场合应用广泛[1-4]。共形阵方向图综合的目的在于为共形阵系统设计一组复加权矢量,使该系统产生的方向图满足期望要求,包括主瓣指向、主瓣宽度、旁瓣电平大小以及在特定方向上形成零陷。传统的契比雪夫方法[5]和泰勒方法[6]不适用于共形阵。采用内点法求解的凸优化方法[7-8]能有效压低旁瓣,但计算复杂一般需要借助凸优化工具。在旁瓣区域添加虚拟干扰同样能够实现方向图综合,如何通过迭代控制干扰功率成为该方法的关键。Olen和Compton提出了较为系统的迭代方法[9],但该方法缺乏主瓣控制。结合粒子群优化算法和遗传算法[10-13]能很好地控制干扰功率,但该类方法一般收敛较慢。基于线性约束最小方差 (Linear constraint minimum variance, LCMV) 准则,Guo等提出了LCMV方向图综合算法(LCMV-pattern synthesis, LCMV-PS)[14],但该算法对迭代系数的选择依赖性太强,降低了其适用性。本文针对LCMV-PS的弊端,对其迭代过程进行改进,结合二分查找方法,不断缩小虚拟干扰功率的取值区间,直至收敛,从而建立了快速收敛的虚拟干扰功率控制机制,降低了对迭代系数选择的依赖性。
1 圆弧阵列数学模型
圆弧阵列是共形阵的基础,复杂的共形阵可由多个圆弧阵组合而成。如图1所示,考虑具有M个接收阵元(如麦克风)的圆弧阵列,该圆弧阵列与一个直线阵相切,且处于同一水平面上。直线阵的每一个阵元沿着水平面垂直后移,得到圆弧上相应阵元的位置。波达方向为θ的信号对应的导向矢量为
(1)
式中:pi(θ)为阵元i的单独响应,对于全向性阵元,可认为pi(θ)=1。τi(θ)为阵元i到空间参考点的相对时延,分为两部分:阵元到直线阵上对应阵元的延时,以及直线阵上对应阵元到参考点的延时,即
(2)
式中:τ1i(θ)=ricosθ/c,ri为直线阵上对应阵元到参考点的距离(图1选择阵列中心为参考点)。τ2i(θ)在图1中根据几何关系可知
(3)
式中:R为圆弧阵的半径,Δr为图1中标识出的对应阵元的距离。
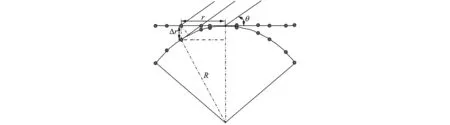
图1 圆弧阵列模型Fig.1 Circular arc array model
2 线性约束最小方差准则(LCMV)方向图综合
2.1 LCMV-PS算法分析
文献[14]提出的基于LCMV的方向图综合算法(LCMV-PS),通过在旁瓣区域施加虚拟干扰,结合LCMV波束形成方法,使系统方向图逼近期望的方向图。虚拟干扰的功率大小通过迭代进行调整,在实际旁瓣电平大于参考电平(预先设定的期望旁瓣电平)的位置加大虚拟干扰的强度,在小于参考电平的位置减小虚拟干扰的强度,直至收敛。可总结其步骤如下。
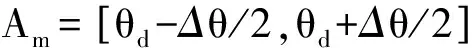
(2)设定初始干扰功率大小f0(θ),θ=θ1,…,θN,N为各角度均匀分布的虚拟干扰的数量。若θ∈Am,则f0(θ)=0,否则f0(θ)=1。
(3)计算数据协方差矩阵Rx,即
(4)
式中:A=[a(θ1),…,a(θN)]为阵列的方向矩阵。k为当前迭代次数。未进行迭代时k=0。σ取一个很小的常数,I为单位矩阵。
(4)利用LCMV波束形成算法计算出加权矢量w。
(5)根据下面的迭代公式计算第k次迭代后,旁瓣区域各角度的干扰功率
(5)

(6)如果综合方向图与期望方向图的差值满足收敛条件,则结束迭代,否则转向(3)步继续,直至收敛或达到设定的最大迭代次数。LCMV-PS算法的关键在于第(5)步中选取的迭代公式,将其主要部分化简为
(6)
当Pk-1(θ)>Pr时,综合方向图在θ处的旁瓣电平大于参考电平,故增大该处的虚拟干扰功率(乘以一个大于1的因子),反之减小该处的虚拟干扰功率(乘以一个小于1的因子)。并且,Pk-1(θ)与Pr越接近,则虚拟干扰功率的调整幅度越小,使虚拟干扰功率的取值更精确。
然而,该方法对迭代系数的选择具有很强的依赖性,K只能在很小的范围内取值。Pk-1(θ) 2.2 改进的LCMV-PS算法 算法的弊端源于式(5),一旦K较大且Pk-1(θ) (7) (8) 式中:formula(6)表示公式(6)。可以解释为,一旦出现式(6)小于或等于0的情况,即将该角度处判定因子置1,且无论后面迭代结果如何,判定因子一旦被置1,就保持不变。判定因子为1处的迭代将使用二分查找,查找区间的上下限(初始值分别为0和1)表示为 (9) (10) 式(6)小于或等于0时,表明此时虚拟干扰功率偏小,因此更新取值区间的下限φk(θ),反之更新取值区间的上限φk(θ)。 与改进前的迭代公式相比,二分查找利用了迭代过程中每一次对取值区间的计算,不断缩小虚拟干扰功率的取值区间,取值区间具有稳定性,不会发生突变,因而降低了对K的取值依赖性。故可以适当增大K值以减少迭代次数,加快收敛。 3.1 仿真条件 利用MATLAB平台进行仿真实验,验证本文方法的有效性。并重点比较了本文方法和文献[14]方法在收敛性和迭代系数K选取上的差异。选取一个对应于均匀线阵的圆弧阵列,阵元数为16,对应均匀线阵的阵元间距为半波长,主瓣指向90°,主瓣宽度为30°,在30°和150°置0,旁瓣电平较主瓣低-40 dB。 3.2 实验结果 图2 本文方法迭代过程中的方向图图3 本文方法收敛后各角度干扰功率值Fig.2 Pattern synthesis for the method proposedFig.3 Power of virtual interference in each azimuthin this paper for the method proposed in this paper 图4 文献[14]方法方向图随迭代系数变化图5 本文方法方向图随迭代系数变化Fig.4 Pattern synthesis varing with K for theFig.5 Pattern synthesis varing with K for the method in Ref.[14] method proposed in this paper 图6给出了文献[14]方法和本文方法在收敛速度上的差异。对于文献[14]方法,选取不同的K值,至少需要19次才能收敛;本文方法可将K增加,取K=150时,只需10次迭代就能收敛,提升了收敛速度。 图6 方向图综合误差随迭代次数变化Fig.6 Composition error of pattern synthesis varing with iterations 针对LCMV-PS算法对迭代系数依赖性强以及收敛慢的缺陷,本文提出了一种改进的共形阵方向图综合方法。利用线性约束最小方差准则确定每一次迭代的复加权矢量,进一步得到实际方向图与理论方向图在各角度的差值。并根据差值的正负号设定判定因子,通过判定因子决定对虚拟干扰功率的取值进行线性调整或二分查找调整,不断缩小虚拟干扰功率的取值区间,直至收敛。在保证有效性的基础上,大大降低了迭代次数,提高了收敛速度,并降低了迭代系数对方向图综合效果的影响,增强了该综合算法的适应性。 [1] Josefsson L, Persson P. Conformal array antenna theory and design[M]. Hoboken: John wiley & Sons, 2006. [2] Haupt R L. Antenna arrays: A computational approach[M]. Hoboken: John Wiley & Sons, 2010. [3] 李海林, 周建江, 谭静, 等. 基于MOPSO算法的卫星共形阵列天线多波束形成[J]. 数据采集与处理, 2014, 29(3): 415-420. Li Hailin, Zhou Jianjiang, Tan Jing, et al. Multi-beam forming of satellite conformal array antenna based on multi-objective particle swarm optimization[J]. Data Journal of Acquisition and Processing, 2014, 29(3): 415-420. [4] 吴仁彪, 卢晓光, 李海, 等. 机载前视风切变检测气象雷达的研究进展[J]. 数据采集与处理, 2014, 29(4): 496-507. Wu Renbiao, Lu Xiaoguang, Li Hai, et al. Overview on airborne forward-looking weather radar with windshear detection capability[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 496-507. [5] Dolph C L. A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level[J]. Proceedings of the IRE, 1946, 34(6): 335-348. [6] Taylor T T. Design of line-source antennas for narrow beamwidth and low side lobes[J]. Antennas and Propagation Transactions of the IRE Professional Group on, 1955, 3(1): 16-28. [7] Tsui K M, Chan S C. Pattern synthesis of narrowband conformal arrays using iterative second-order cone programming[J]. Antennas and Propagation IEEE Transactions on, 2010, 58(6): 1959-1970. [8] Nai S E, Ser W, Yu Z L, et al. Beampattern synthesis for linear and planar arrays with antenna selection by convex optimization[J]. Antennas and Propagation IEEE Transactions on, 2010, 58(12): 3923-3930. [9] Olen C A, Compton Jr R T. A numerical pattern synthesis algorithm for arrays[J]. Antennas and Propagation IEEE Transactions on, 1990, 38(10): 1666-1676. [10]Li W, Hei Y, Shi X, et al. An extended particle swarm optimization algorithm for pattern synthesis of conformal phased arrays[J]. International Journal of RF and Microwave Computer—Aided Engineering, 2010, 20(2): 190-199. [11]Jayaprakasam S, Rahim S K A, Yen L C, et al. Genetic algorithm based weight optimization for minimizing sidelobes in distributed random array beamforming[C]∥Parallel and Distributed Systems (ICPADS), 2013 International Conference on. [S.L.]:IEEE, 2013: 623-627. [12]Wang W B, Feng Q, Liu D. Application of chaotic particle swarm optimization algorithm to pattern synthesis of antenna arrays[J]. Progress in Electromagnetics Research, 2011, 115: 173-189. [13]和洁, 冯大政, 李晓明. 基于遗传算法和禁忌搜索的MIMO雷达天线布阵优化[J]. 数据采集与处理, 2011, 26(4): 413-419. He Jie, Feng Dazheng, Li Xiaoming. Optimization of antenna array of MIMO radar based on genetic algorithm and tabu search[J]. Journal of Data Acquisition and Processing, 2011, 26(4): 413-419. [14]Guo Q, Liao G, Wu Y, et al. Pattern synthesis method for arbitrary arrays based on LCMV criterion[J]. Electronics Letters, 2003, 39(23): 1628-1630. 夏欢(1989-),男,硕士研究生,研究方向:信号与信息处理,E-mail:nju_xh@126.com。 张兴敢(1956-),男,教授,研究方向:信号与信息处理。 柏业超(1984-),男,副教授,研究方向:信号与信息处理。 Improved Method for Conformal Array Pattern Synthesis Xia Huan, Zhang Xinggan, Bai Yechao (School of Electronic Science and Engineering, Nanjing University, Nanjing, 210023,China) Conformal arrays, with more flexible placement than traditional array, are widely used in many areas. However, pattern synthesis of conformal array is more complex and some traditional pattern synthesis methods are not applicable. Applying virtual interference in the region of the side lobe is proved to be feasible. Then the critical issue is to find effective methods to determine the power of virtual interference in each azimuth through an iterative process. Generally, existing iterative methods have slow convergence rate or heavy computation. An improved method for conformal array pattern synthesis is proposed based on linearly constrained minimum variance (LCMV) criterion and the method is applicable to any array placement. Moreover, it can accelerate the convergence rate and reduce the dependence on the iteration coefficient for adaptive beam-formers. Numerical examples are provided to demonstrate the effectiveness of the method. conformal array; pattern synthesis; virtual interference; linearly constrained minimum variance (LCMV) 江苏省产学研前瞻性联合研究(BY2012187)资助项目。 2014-07-17; 2014-10-10 TN958.92 A
3 仿真实验
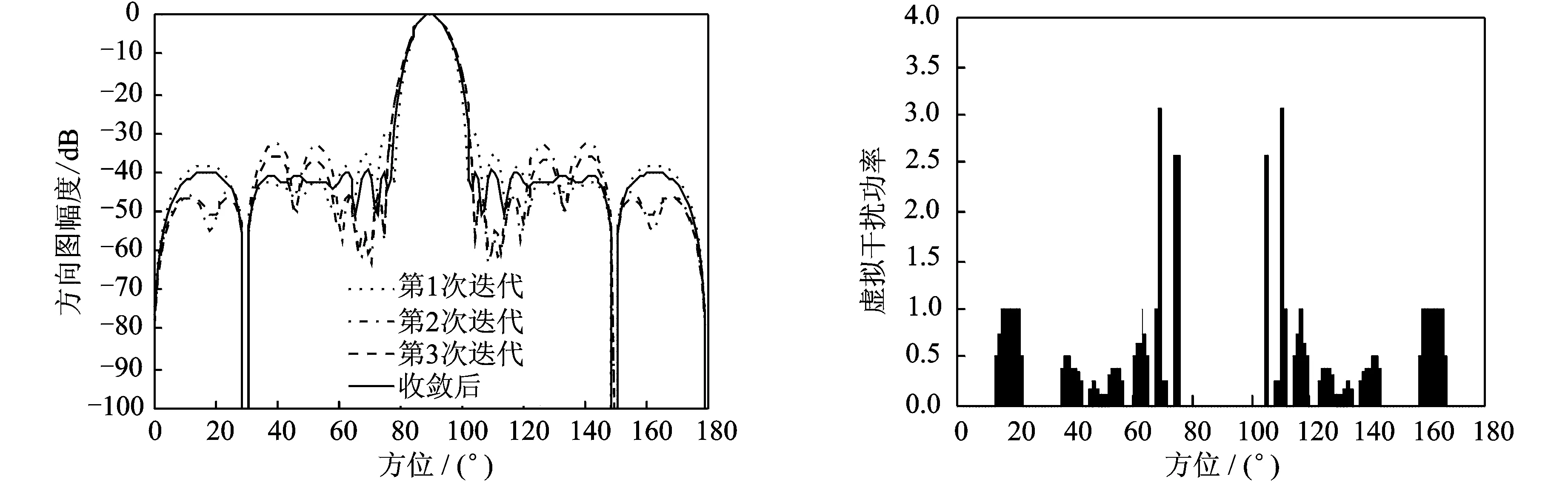
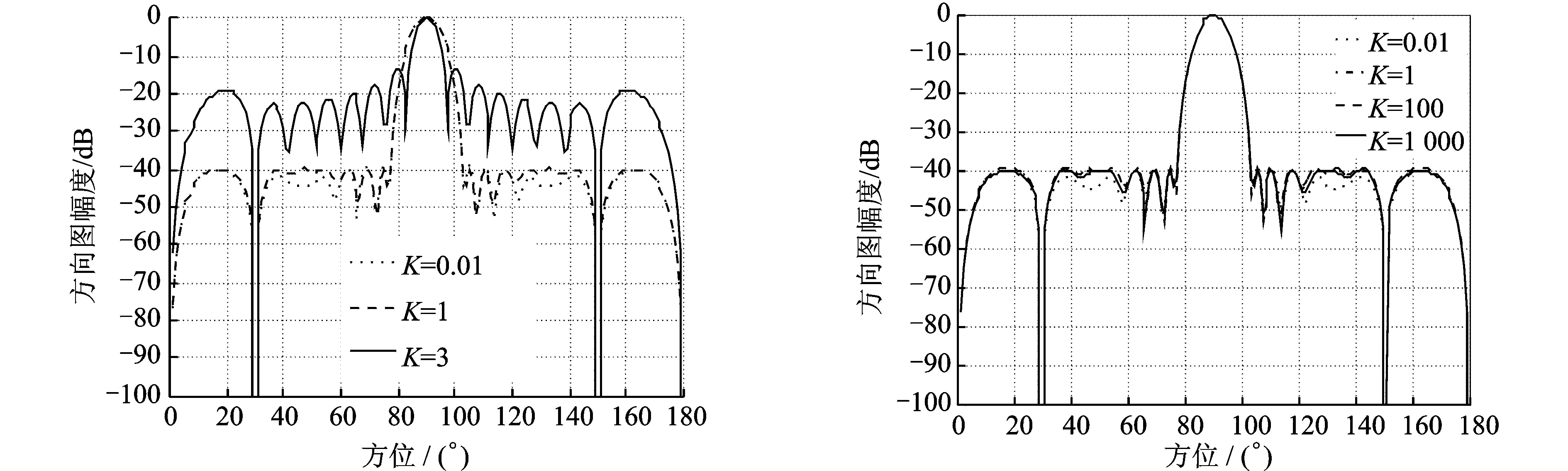

4 结束语




