基于加权多尺度张量子空间的人脸图像特征提取方法*

王仕民 程柏良 叶继华 王明文

(江西师范大学计算机信息工程学院，南昌，330022)



基于加权多尺度张量子空间的人脸图像特征提取方法*

王仕民 程柏良 叶继华 王明文

(江西师范大学计算机信息工程学院，南昌，330022)

为了不破坏原始数据固有的高阶结构和数据之间的相关性，减少光照对图像特征的影响，并优化多尺度特征的权重，提出了基于加权多尺度张量子空间的图像特征提取方法。采用多尺度小波变换表征图像各个部位特征，使用不确定度权衡每个尺度对图像分类的作用，并组建成多尺度张量子空间，结合多线性主成分分析与线性判别分析算法，降低了图像在处理过程中的成本，保存了高维数据固有结构和相关性，完成对图像特征提取。使用CAS-PEAL-R1东方人脸库进行评测，实验结果表明，该图像特征提取算法用于图像识别过程中具有较好的效果，具有一定的可行性。

图像特征；多尺度变换；张量子空间；多线性主成分分析 ；不确定度

引 言

近年来，图像特征提取引起了计算机领域学者的广泛关注，其作为图像识别、图像处理和图像理解等领域研究的基础，在科学研究、社会安全、软件开发和航空航天等项目中有着广阔的应用前景。但是，图像特征的描述和提取问题却成为了图像处理和识别过程中遇到的一个的瓶颈，所以对图像特征进行有效表示和提取一直都是图像理解和识别的热点。

引入多尺度Gabor小波，能够解决图像特征提取过程中存在的问题，对光照变化不敏感，能够提供对光照变化良好的适应性且能容忍一定程度的图像旋转和变形，这样能提高算法的鲁棒性[1]。最近，基于局部二值模式(Local binary patterns, LBP)[2,3]的Gabor特性方法被提出,例如局部Gabor二进制模式(Local Gabor binary patterns, LGBP)[4]和Gabor相位模式的直方图(Histogram of Gabor phase patterns, HGPP)[5]。上述提出的方法都能较好地表征图像，并获得较好的识别效果，但是使用多尺度Gabor滤波器，更大程度上利用了图像的频带特征，涉及中心频带和方向的选择，计算过程比较复杂，从而容易发生数据灾难，所以高维数据降维算法并提取图像的特征完成识别成为了研究重点。传统的主成分分析(Principal components analysis, PCA)[6]和线性判别分析(Linear discriminant analysis, LDA)[7]算法，这些线性特征提取算法需要将图像矢量化变成一维数据，处理过程必然破坏了原始数据的结构及相关性，并且处理过程非常复杂、需求占据大量内存。二维主成分分析(Two-dimensional principal component analysis, 2DPCA)[8]等算法的出现，一定程度上解决了上述问题，2DPCA降维过程中直接处理二维矩阵，不仅很好地保存了高维图像数据之间的内部结构，而且还提高了工作效率和算法性能，但是面对高维图像，二维主成分分析像主成分分析一样，同样出现不足与弊端。而近年来出现的张量子空间降维算法，把多尺度图像数据存储于张量空间中，很好地保存了图像自然多维结构及相关性，并成为科研热点。文献[9]将一个张量分解成一些矩阵的外积与一个核张量，其主要是将图像直接转化成张量空间，其算法分解过程一定程度上可以看成是PCA的高阶推广，这样势必导致高维向量的产生。针对高维奇异值分解分解这个难点，文献[10，11]提出了各种奇异值分解算法。Yan等[12]提出了多重线性判别分析的子空间学习方法，其中使用了k-mode优化沿着不同的张量方向展开张量，通过迭代的过程完成并通过子空间学习用于图像识别过程。Kotsia为了避免秩-支持张量机对判别信息造成丢失过多，提出了另一种模型即高秩支持张量机，很好地解决了过多信息丢失的问题[9，13]。近年来，基于张量的降维方法取得了一系列的成果[14-16]。基于张量的机器学习方法在社会应用领域(尤其是医学领域)，已经取得了非常成功的应用，比如使用张量机器学习方法对脑电波图谱和核磁共振分析等[17]，解决了医学上急迫的问题，方便了医生对病人病情的诊断。

为了不破坏原始数据固有的高阶结构和数据之间的相关性，减少光照对图像特征的影响，并优化多尺度特征的权重，采用了多尺度Gabor变换获取图像多尺度特征，并通过使用不确定度计算各个多尺度特征的权重，优化了各个纹理特征在图像识别中的作用，并组建成张量空间，通过使用多线性主成份分析(Multiple linear principle component analysis, MPCA)算法[18]和线性判别分析算法把高维构建的张量空间降维成低维数据，提取得到较好表征图像数据的特征，完成最终的图像特征提取。本算法使用CAS-PEAL-R1东方人脸库[19]完成测试，结果表明，该图像特征提取算法用于图像识别过程中具有较好的效果，具有一定的可行性。

1 图像的多尺度变换

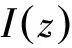
(1)

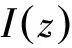
为了尽可能完整地得到图像的纹理特征，在实验过程中通常使用多个中心尺度和多个方向组合，完成图像纹理特征的获取，其中方向的变化u∈(0,1,2,3,4,5,6,7)，卷积后图像的纹理方向也会随着变化，如图1所示。从图1中可以看出，当使用滤波器方向和图像纹理特征的方向一致时，得到的滤波特征响应比较明显。

图1 方向响应特征Fig.1 Direction response features

同理，当中心尺度变化v∈(0,1,2,3,4)时，图像与核函数卷积后图像的纹理方向也会随着变化，具体结果如图2所示。

图2 中心尺度响应特性Fig.2 Center-scale response features

2 加权多尺度张量子空间及降维算法

2.1 不确定度权值计算

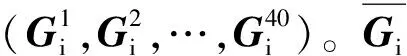
(2)

则第j个Gabor滤波器的不确定度uj的计算过程为

(3)

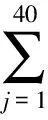
(4)

且图像样本Yi经过Gabor滤波响应后的方差为

(5)

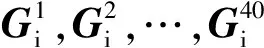
(6)

把不确定度代入，得到

(7)

为了使计算机结果方差最小，使用拉格朗日乘法完成计算，γ为拉格朗日常数，有

(8)

求解得到权值计算公式为

(9)

2.2 多线性主成分分析投影映射及降维

本节通过使用多线性主成分分析(Multi-linear principal component analysis，MPCA)对高维张量空间数据进行降维，得到数据结构相关及低维数据。MPCA算法的简要过程如下。

有M个张量样本{Xm,m=1,…,M}作为训练样本，且Am∈RI1 ×I2 ×…×IN，即构建的张量空间属于张量空间RI1⊗RI2…⊗RIN，其中In作为张量第n模的维数。多线性主成分分析的最终结果是计算出一个多线性变换空间{U(n)∈RIn×Pn,n=1,2,…,N}且获取了原始张量中大部分特征。它通过最大化张量总的散布值ψY，U(n)就由Φ(n)中最大的pn个特征值对应的pn个特征向量构成[18]，有

(10)

(11)

(12)

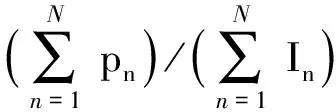
3 加权多尺度张量子空间的图像特征提取与识别

本文提出了加权多尺度张量子空间的图像特征提取与识别算法，采用了多尺度Gabor变换获取图像多尺度特征，并通过使用不确定度计算各个多尺度特征的权重，优化了各个纹理特征在图像识别中的作用，并组建成张量空间，通过使用MPCA算法和线性判别分析算法把高维构建的张量空间降维成低维数据，提取得到较好表征图像数据的特征，最后使用LDA和最近邻算法完成图像识别过程。具体的识别过程算法描述如下。

{Vm,m=1,2,…,M};图像训练样本集

{Xm,m=1,…,M};构建得到样本的张量形式

ProgramSub_tensor_featuresBegin

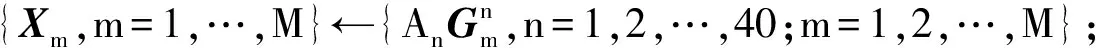
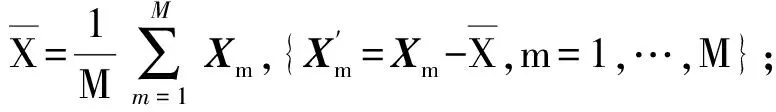
pn←Qmethod[9];使用Q方法计算张量子空间维数

forn=1topn

{U(n),n=1,2,…,N}←Φ(n)*;奇异值分解得到特征向量

endfor

Ym=Xm×1U(1)T×2U(2)T×…×NU(N)T;样本投影映射后的张量集

fork=1:K;通过使用交替最小二乘法算法，直到结果收敛

forn=1: N;设置U(n)由Φ(n)*中最大的pn个特征值对应的pn个特征向量构成

ifψYk-ψYk-1≥ηdo;(η通常取值为10-6)

else exit

end if

end for

end for

Ym=Xm×1U(1)T×2U(2)T×…×NU(N)T;完成特征提取过程

ym←Ym;重新排列成一个特征矩阵

zm=Vldaym;投影空间Vlda，求得最后投影空间

end Program Sub_tensor_features

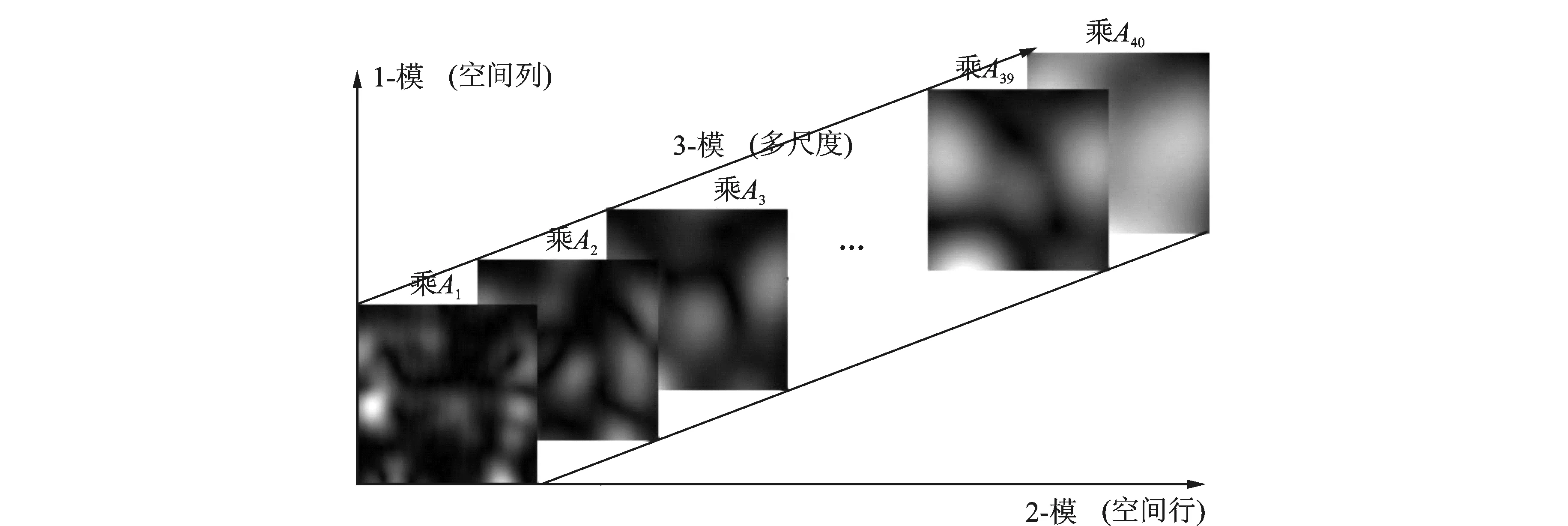
图3 多尺度Gabor特征加权构造张量空间Fig.3 Tensor space of weighted multi-scale Gabor features

4 实验结果

4.1 图像库与预处理

图像库作为图像识别算法评测过程的测试对象，具有非常重要的意义。本算法使用了东方人脸库CAS-PEAL-R1[19]完成实验测试。东方人脸库图像都是在某种特定环境中采集获取，包含表情、饰物、姿势、光照4种环境情况。通过对CAS-PEAL-R1解释文献分析发现：光照的变换对人脸识别影响较大，其识别率都比较低，而本算法的识别算法中充分考虑了光照等外界环境对识别的干扰。东方人脸库CAS-PEAL-R1的光照子图库中部分人脸如图4所示。

图4 CAS-PEAL-R1光照的子图像库中部分人脸Fig.4 Partial faces of CAS-PEAL-R1 illumination image sub-library

东方人脸库CAS-PEAL-R1中图像的大小为640×480像素，其中包含和多种背景图信息，为了提高算法的运行效率，降低实验运算量，本算法对原图进行了一定的预处理：本算法采用基于Haar的人脸检测算法[21]，把图像中人脸检测出来，并替代原始样本；实验过程中，可能会得到人脸图像大小不一致，统一将人脸图像大小设置为64×64像素。实验过程中预处理后部分图如图5所示。

图5 预处理后部分人脸Fig.5 Partial faces after preprocessing

4.2 识别算法比较

为了说明本文算法对人脸特征提取的有效性，将与一些基础的人脸特征提取算法(PCA，PCA+LDA，MPCA+LDA和GPCA+LDA (Gabor+PCA+LDA))进行识别率比较，实验过程中都使用东方人脸库CAS-PEAL-R1中光照子图像库。实验训练过程中，使用东方人脸库光照子图像库中每类人脸样本数为变化的r用于训练，其值分别为{r=1,2,…,6}，则相对应剩下部分全部用于识别率测试。在CAS-PEAL-R1光照子库上识别算法识别率比较图如图6所示。

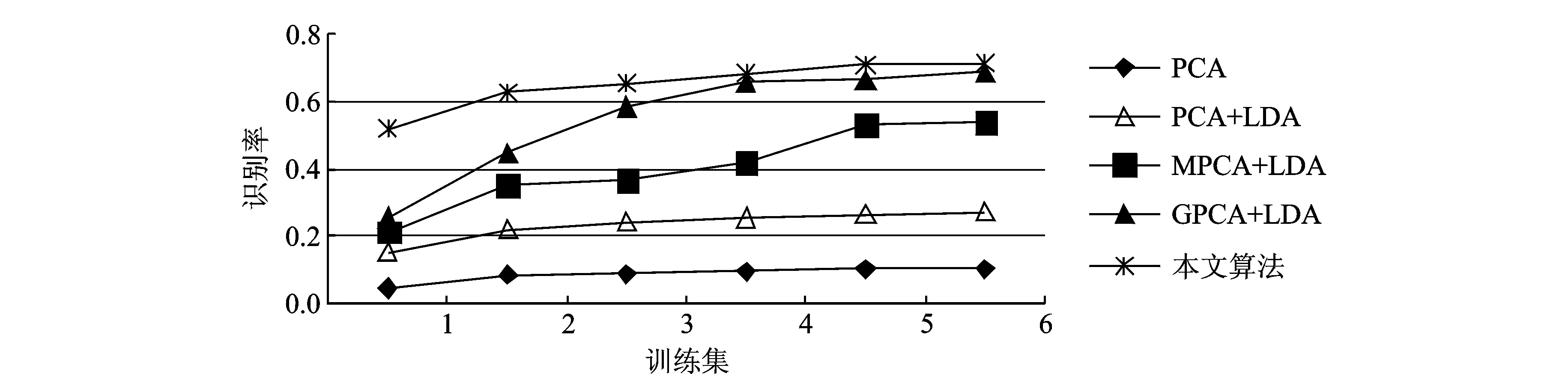
图6 人脸识别率比较图Fig.6 Comparison of face recognition rate

由图7可以看出：(1)外界噪声和环境光照的变化对图像识别的影响比较严重，相对恶劣光照环境下的图像识别率还是比较低，并仍然是一个难点；(2)由于多尺度Gabor小波变换对于光照变化不敏感，并能较好提取图像内部各个尺度的特征，Gabor小波变换的引入，能够提供对光照变化良好的适应性，这样能提高算法的鲁棒性，其识别率也明显提升；(3)由于PCA和LDA算法都需要对图像进行矢量化，必然会破坏原始图像数据之间内部结构信息及相关性，其识别率肯定会受影响，导致识别率不高；(4)本文算法直接操作图像多尺度序列的张量而不是它们进行拉伸后的向量形式，通过多尺度变换组建张量空间，同时使用了不确定度权衡了多尺度的权值，保存了完整的多尺度图像特征，并采用MPCA多线性主成分算法降维并提取图像特征，最终得到能较好表征原始图像的特征，提高识别率。

本实验所用的仿真环境是清华同方I5处理器，内存为4 GB的个人计算机，采用Matlab2011b编程。在CAS-PEAL-R1光照子库上，经典算法(PCA，GPCA (Gabor+PCA)，GMPCA(Gabor+MPCA))和本文算法(每类人脸样本数r=5)识别所用时间比较如表1所示。

表1 本文算法与经典算法识别所用时间比较表

从表1可以看出：(1)实验过程中，多尺度Gabor变换会消耗大量的时间，引入多尺度变换将加大运算量；(2)采用GPCA的训练时间远远大于采用GMPCA的训练时间，这是因为采用GMPCA时，不需要将样本变成一维数组，导致用于计算特征子空间的基向量的样本图像协方差矩阵维数变小；(3)测试过程中，由于GMPCA所需要的用于存储特征矩阵的存储空间比前者大得多, 这样就导致了GMPCA的测试时间略大于GPCA的测试时间；(4)综合图7和表1，虽然本文算法和GMPCA运行时间相似，但是本文算法的识别率却较好，所以该基于加权多尺度张量子空间的图像特征提取算法用于图像识别过程中具有较好的效果，具有一定的可行性。

5 结束语

本文算法为了不破坏原始数据固有的高阶结构和数据之间的相关性，减少光照对图像特征的影响，并优化多尺度特征的权重，采用了多尺度Gabor变换获取图像多尺度特征，并通过使用不确定度计算各个多尺度特征的权重，优化了各个纹理特征在图像识别中的作用，并组建成张量空间，通过使用MPCA算法和线性判别分析算法把高维构建的张量空间降维成低维数据，提取得到较好表征图像数据的特征，完成最终的图像特征提取。本算法使用CAS-PEAL-R1东方人脸库完成测试，结果表明，该图像特征提取算法用于图像识别过程中具有较好的效果，具有一定的可行性。

[1] 宋传鸣,赵长伟,刘丹,等.3D 多尺度几何分析研究进展[J]. 软件学报,2015,26(5):1213-1236.

Song Chuanming, Zhao Changwei, Liu Dan, et al. Advances in three-dimensional multiscale geometrical analysis[J]. Journal of Software, 2015,26(5):1213-1236.

[2] 宋克臣, 颜云辉, 陈文辉, 等. 局部二值模式方法研究与展望[J]. 自动化学报, 2013, 39(6): 730-744.

Song Kechen, Yan Yunhui, Chen Wenhui, et al. Research and perspective on local binary pattern[J]. Acta Automatica Sinica, 2013, 39(6): 730-744.

[3] 黄兵,郭继昌. 基于Gabor小波与LBP直方图序列的人脸年龄估计[J]. 数据采集与处理, 2012, 27(3):340-345.

Huang Bing,Guo Jichang. Age estimation of facial images based on Gabor wavelet and histogram sequence of LBP [J]. Journal of Data Acquisition and Processing, 2012, 27(3):340-345.

[4] Zhang W, Shan S, Gao W, et al. Local Gabor binary pattern histogram sequence (LGBPHS): A novel non-statistical model for face representation and recognition[C]∥Proceedings of the IEEE International Conference on Computer Vision (ICCV). Beijing, China: IEEE Computer Society Press, 2005:786-791.

[5] Zhang B, Shan S, Chen X, et al. Histogram of Gabor phase patterns (HGPP): A novel object representation approach for face recognition[J]. IEEE Trans Image Process, 2007,16(1): 57-68.

[6] Turk M, Pentland A. Face recognition using eigenfaces [J]. Cogn Neurosci, 1991, 3(2): 71-86.

[7] Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection[J]. IEEE Trans Pattern Anal Mach Intell, 1997,19(7):711-720.

[8] Jian Yang. Two-dimensional PCA:A new approach to appearance-based face representation and recognition [J]. Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137.

[9] Kotsia I, Patras I. Support tucker machines[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recogition. Colorado, USA: IEEE Computer Society Press, 2011: 633-640.

[10]Li Qun, Shi Xiangqiong, Schonfeld D. Robust HOSVD-based higher-order data indexing and retrieval[J]. IEEE Signal Processing Letters, 2013,20(10): 984-987.

[11]Rajwade A, Rangarajan A, Banerjee A. Image denoising using the higher order singular value decomposition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(4):984-987.

[12]Yan S, Xu D, Yang Q, et al. Multilinear discriminant analysis for face recognition[J]. Trans Image Process, 2007, 16(1): 212-220.

[13]Guo Weiwei, Kotsia I, Patras I. Tensor learning for regression[J]. IEEE Transactions on Image Processing, 2012, 21 (2): 816-827.

[14]Kotsia I, Guo Weiwei, Patras I. Higher rank support tensor machines for visual recognition[J]. Patter Recognition, 2012, 45 (12): 4192-4203.

[15]Gao Chao,Wu Xiaojun. Kernel support tensor regression [J]. Procedia Engineering, 2012,29(4): 3986-3990.

[16]Wang Z, He X S, Gao D Q, et al. An efficient kernel-based matrixized least squares support vector machine[J]. Neural Computing and Applications, 2013, 22: 143-150.

[17]Signoretto M, De Lathauwer L, Suykens J A K. A kernel-based framework to tensorial data analysis[J]. Neural Networks, 2011, 24: 861-874.

[18]Lu Haiping, Plataniotis K N, Venetsanopoulos A N. MPCA: Multilinear principal component analysis of tensor objects[J]. IEEE Trans on Neural Networks, 2008, 19(1):18-39.

[19]Gao Wen, Cao Bo, Shan Shiguang, et al. The CAS-PEAL large-scale Chinese face database and baseline evaluations[J]. IEEE Trans on System Man, and Cybernetics (Part A), 2008, 38(1):149-161.

[20]王仕民, 叶继华, 邓涛, 等. 2维双树复小波不确定度加权融合的人脸识别[J]. 中国图象图形学报, 2012, 17 (8): 995-1001.

Wang Shimin, Ye Jihua, Deng Tao, et al. Two-dimensional dual-tree complex wavelet transform uncertainty weighted fusion in face recognition[J]. Journal of Image and Graphics, 2012, 17 (8): 995-1001.

[21]江伟坚, 郭躬德, 赖智铭. 基于新Haar-like特征的Adaboost人脸检测算法[J]. 山东大学学报：工学版, 2014, 44 (2),43-48.

Jiang Weijian, Guo Gongde, Lai Zhiming. An improved Adaboost algorithm based on new Haar-like feature for face detection [J]. Journal of Shandong University: Engineering Science, 2014,44(2):43-48.

王仕民(1986-)，男，实验师，研究方向：图像处理，wsmyangxi@126.com。

王明文(1964-)，男，教授，博士生导师，研究方向：数据挖掘和信息检索。

程柏良(1978-)，男，博士，研究方向：可信计算。

叶继华(1966-)，男，教授，研究方向：图像处理。

Method for Face Image Feature Extraction Based on Weighted Multi-Scale Tensor Subspace

Wang Shimin, Cheng Bailiang, Ye Jihua, Wang Mingwen

(College of Computer Information and Engineering, Jiangxi Normal University, Nanchang, 330022, China)

In order to keep the inherent higher order structure and correlation in the original data, reduce the influence of illumination in image recognition, and optimize the weight of the multi-scale feature, the method of image feature extracting based on weighted multi-scale tensor subspace is proposed to solve the problems. Firstly, multi-scale transform is used to characterize each place feature of the image, and uncertainty weighed is adopted on the role of each scale feature for image classification. And then a multi-scale tensor space is built using multiple linear principal component analysis and linear discriminant analysis algorithm to reduce the cost of processing, preserving the inherent structure and correlation of high-dimensional data. Finally, the extraction of the image features is completed. CAS-PEAL-R1 oriental face database is chosen for evaluation. The experimental results show that the algorithm performs better than some recent algorithms for image recognition with practical feasibility.

image feature; multi-scale transform; tensor subspace; multiple linear principle component analysis; uncertainty

国家自然科学基金(61462042,614620145)资助项目。

2015-09-29；

2015-11-02

TP391.41

A