蒸汽冷却带肋矩形通道流动和换热特性数值研究

陈宇佳,杜长河,李亮

(西安交通大学叶轮机械研究所,710049,西安)



蒸汽冷却带肋矩形通道流动和换热特性数值研究

陈宇佳,杜长河,李亮

(西安交通大学叶轮机械研究所,710049,西安)

为了阐明蒸汽冷却带肋矩形通道的换热增强机理,基于三维RANS方程和标准k-ω湍流模型,数值模拟了带肋矩形通道的流场和换热特性,研究了雷诺数、入口宽高比和肋间距对流动和换热特性的影响,进一步分析了努塞尔数与雷诺数、入口宽高比、肋间距之间的关系,由此得出带肋矩形通道的传热关联式。结果表明:肋片的存在破坏了较厚的换热边界层,增强了换热性能。雷诺数增大,平均努塞尔数、综合换热因子均增大,阻力系数小幅上升;宽高比增大,平均努塞尔数、综合换热因子均增大,阻力系数大幅上升;肋间距增大,平均努塞尔数增加,阻力系数先增后减,综合换热因子先减后增。所得传热关联式可为先进燃机蒸汽冷却叶片的设计提供参考。

带肋矩形通道;蒸汽冷却;流动换热;传热关联式;数值模拟

肋片扰流冷却是目前燃气透平中主要的冷却方式,在叶片内部的冷却通道中通过浇铸肋片可以强化换热。蒸汽冷却具有热容量大、传热系数高等优点,因此蒸汽冷却带肋矩形通道已成为当前燃气透平冷却领域的研究热点。

国内外学者对蒸汽冷却带肋矩形通道做了大量的研究工作。史晓军等在内冷通道实验台上研究了宽高比、雷诺数、肋片角度对蒸汽冷却传热和压降的影响,指出60°肋片传热最优[1-2]。Shui等采用实验和数值模拟方法探究了进口压力、蒸汽过热度等因素对流动和传热特性的影响[3-5]。Elwekeel等建立了不同形状肋片的数值模型,发现梯形肋片换热效果最佳[6]。Zhu等发展了微观旋涡分布对换热的影响模型,指出旋涡的数量、强度与换热关系密切[7]。

目前,在蒸汽冷却带肋矩形通道的研究中涉及肋间距对流动和换热影响的研究十分匮乏,而且这些研究中鲜有对带肋壁面局部区域换热增强机理的分析。本文建立了带肋矩形通道的数值模型,探究了雷诺数、肋间距、宽高比对肋片换热和流动阻力的影响,分析了带肋矩形通道的换热机理,拟合了传热的关联式。

1 计算模型和数值方法

带肋矩形通道几何模型如图1所示。带肋顶面和底面各自均匀分布了20个90°直肋片。表1给出了实验条件下[5]带肋矩形通道的几何参数。

图1 带肋矩形通道的几何模型

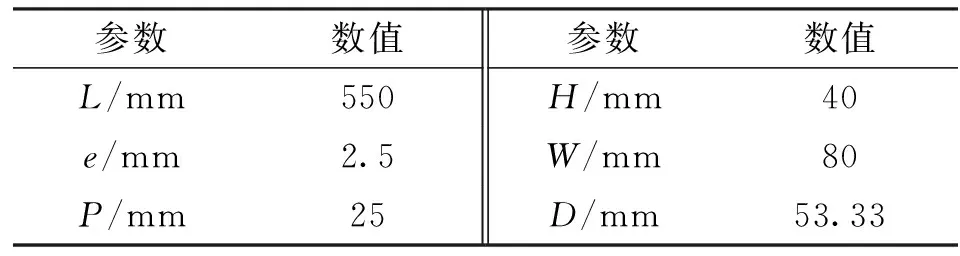
参数数值参数数值L/mm550H/mm40e/mm2.5W/mm80P/mm25D/mm53.33

注:L为通道长度;e为肋宽或肋高;P为肋间距;H为通道高度;W为通道宽度;D为水力直径。

图2给出了使用ICEM软件划分的带肋矩形通道的计算网格。带肋矩形通道的几何形状十分规则,全部使用H型网格即可得到高质量的结构化网格。壁面处网格进行加密处理,第一层网格厚度为0.01 mm,网格增长率为1.5,保证y+<1。边界条件设置如下:壁面热流密度均为6 376 W/m2,入口静压为304.98 kPa,入口静温为177 ℃,通过改变出口流量获得所需雷诺数。

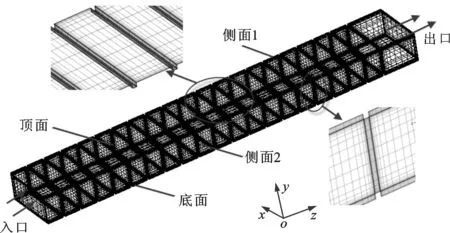
图2 带肋矩形通道的计算网格

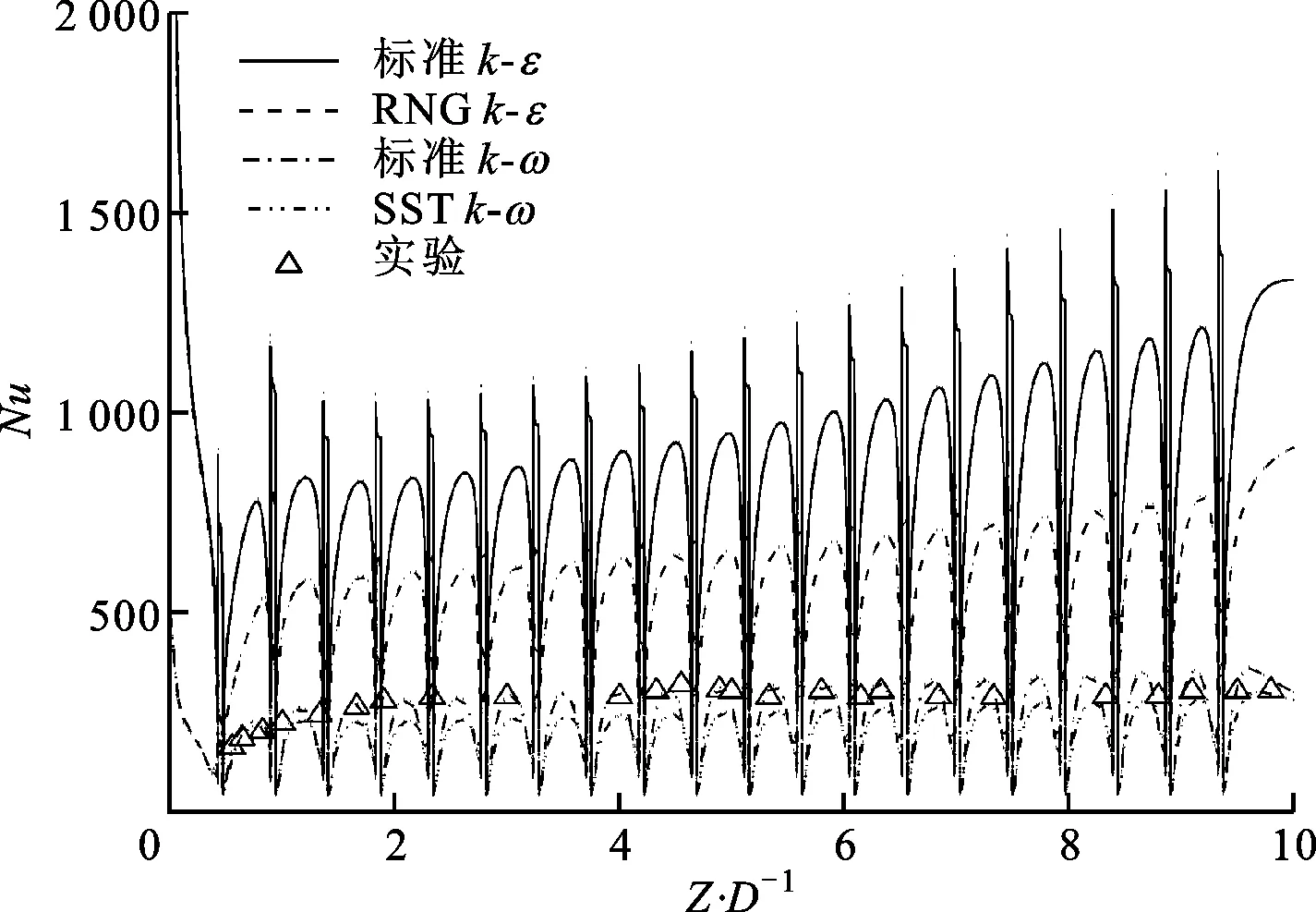
Z:距入口沿z方向的距离图3 带肋底面中线处的Nu与实验数据对比

数值计算时使用ANSYS CFX软件对三维RANS方程和两方程湍流模型进行求解,计算精度为二阶。为了验证数值方法的正确性,采用Steam 1v作为冷却介质,边界条件与Shui等实验情况3[5]一致。图3对比了数值计算与实验测量的带肋底面中线处Nu分布。图3中显示,与实验测量值相比标准k-ε湍流模型的计算结果偏差较大,与标准k-ω湍流模型最为吻合。这是因为标准k-ε湍流模型适用于高雷诺数流动,并假设流动为完全湍流,却忽略了分子间黏性力的影响;标准k-ω湍流模型对低雷诺数情况进行了修改,适用于壁面束缚流动。实验测量情况下,雷诺数较低,肋片扰流持续破坏换热和流动边界层,流动并不是完全湍流,因此出现了图3中的情况。本文采用标准k-ω湍流模型进行了数值计算,并对网格无关性进行了验证,计算时选定的网格节点总数为151万。

2 参数定义

Re=ρVD/μ,其中ρ为入口平均密度,V为入口平均速度,D为水力直径,μ为入口平均动力黏性系数。

Nu=qD/((Tb-(Tin-Tout)Z/L)λ),其中q为热流密度,Tb为底面温度,Tin为入口平均温度,Tout为出口平均温度,Z为距入口沿z方向的距离,L为通道长度,λ为蒸汽热传导率。

阻力系数取f=(pin-pout)D/(2ρLv2),其中pin和pout分别为进、出口静压。

为了综合评价肋片对流动与换热的综合影响,分别以光滑圆管充分发展流动的D-B公式和Blasius阻力系数方程作为参考,即

Nu0=0.023Re0.8Pr0.4

(1)

f0=0.0791Re-0.25

(2)

式中:Pr为带肋通道的体积平均普朗特数。定义综合换热因子为η=(Nua/Nu0)/(f/f0)1/3,其中Nua为带肋底面的平均Nu。

3 结果分析

3.1 换热增强机理分析

通道的带肋顶面和底面在几何上是对称的,因此带肋顶面和底面的流动和换热特性相同。本节以带肋底面为例分析了流动和换热机理,底面上的肋片从左至右分别编号为1～20。图4给出了在验证了的模型边界条件下带肋底面的Nu分布云图。可以看出,底面上均匀分布的肋片持续破坏了流动和换热边界层,湍流强度得以增强。图5给出了yz平面截面上的局部流线与速度云图。下面结合图4和图5,综合分析带肋通道换热增强的机理。

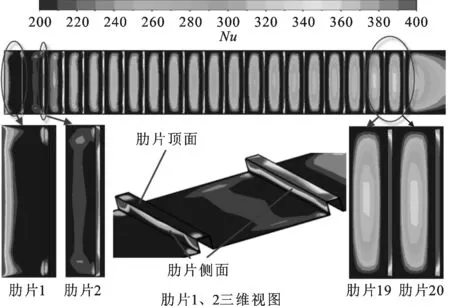
图4 带肋底面的Nu云图

首先观察到图4肋片1中入口段小范围内Nu很高,这是入口效应导致的,入口段流动还未充分发展,流动边界层和换热边界层都很薄,因此换热比较剧烈。随着蒸汽沿着通道前进,热边界层逐渐增厚,进而使Nu逐渐减小。

图4中入口段和肋片1中间区域的Nu没有增长,而肋片1与肋片2之间存在着一个高Nu区域,这是旋涡冲刷底面造成的。结合图5的流线图分析,肋片1左侧仅存在一个很小的旋涡,其余部分的流动是逐渐发展的,热边界层较厚,因此Nu没有升高;肋片1与肋片2之间的旋涡区域很大,旋涡对底面的冲刷破坏了原有的厚换热边界层,由此对流换热能力增强,Nu升高。

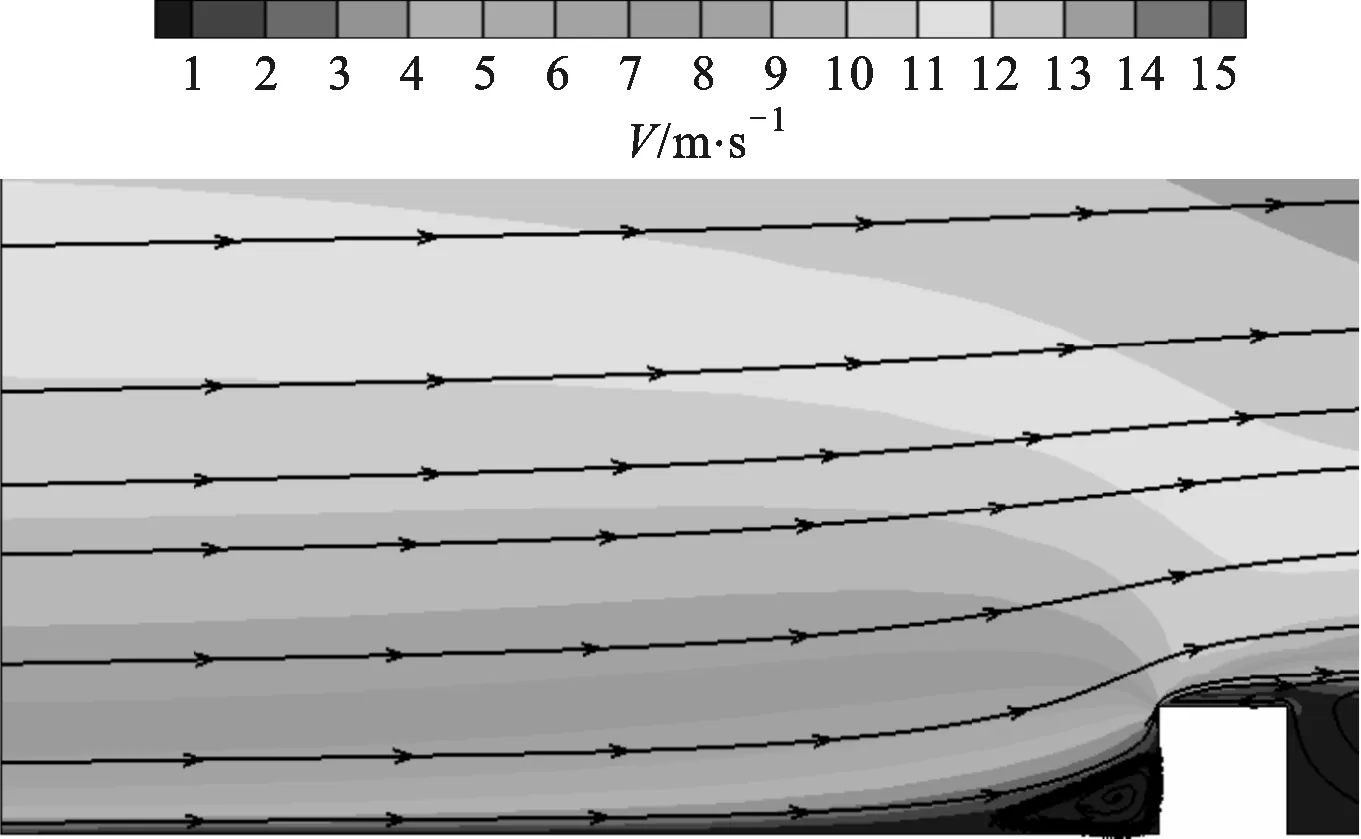
(a)肋片1

(b)肋片2

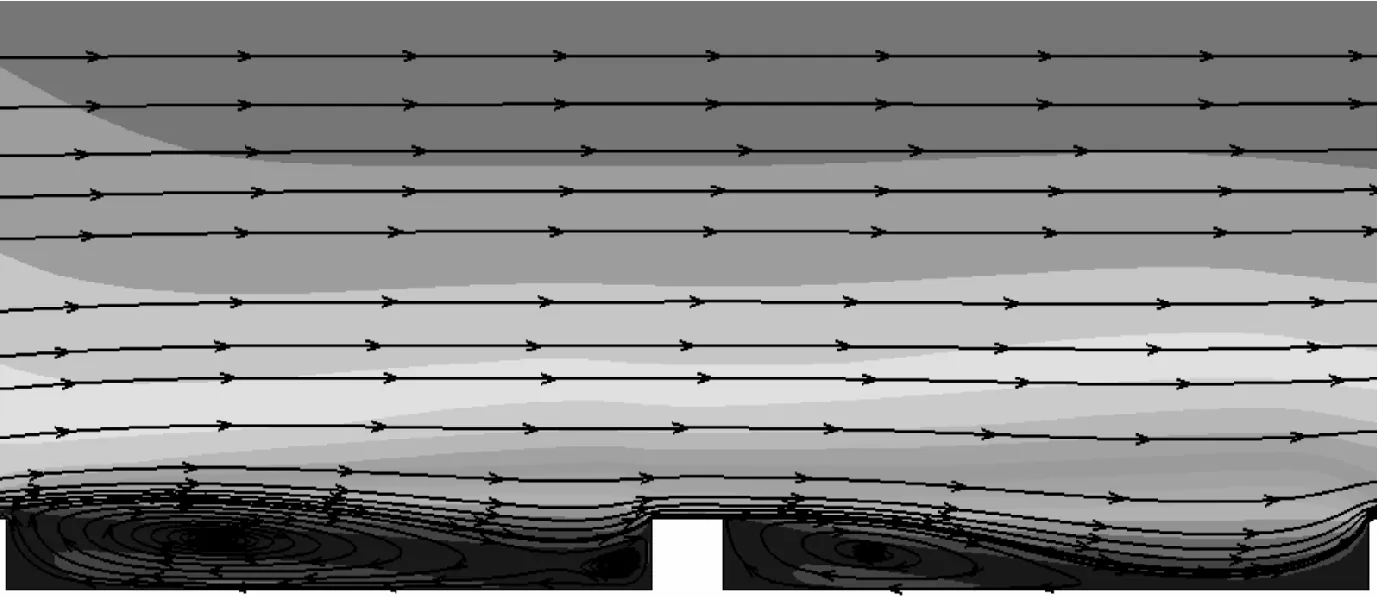
(c)肋片19图5 yz截面局部流线图与速度云图

由图4肋片1、2的三维视图可见,肋片左侧面的Nu均有不同程度提升,这与旋涡冲刷肋片有关。由图5肋片1、2流线可见,肋片左侧面受到了不同程度的旋涡冲击,热边界层被破坏,Nu升高,同时肋片2顶面比肋片1的Nu更高,这是肋片2顶面速度更高的缘故。结合图5速度云图可见,肋片2表面流速远高于肋片1,因而肋片2表面蒸汽湍流强度更大,换热更剧烈。

对比图4肋片19、20之间底面区域和肋片1、2之间底面区域,发现整体上肋片19、20之间底面Nu高于肋片1、2之间底面,这种差异是流动结构的不同产生的。图5中肋片2左侧低速旋涡冲刷底面,而肋片19右侧是高速主流直接冲击底面,主流的湍流强度更大,能进一步减薄热边界层,Nu则随之提高。

3.2 雷诺数的影响

雷诺数会影响蒸汽冷却带肋通道的流动和换热特性,本文通过改变出口流量使雷诺数分别为16 000、36 000、56 000、76 000、96 000,其他几何参数保持不变。图6给出了不同雷诺数下带肋底面的Nu分布云图。由图6可见,随着雷诺数的增大,带肋底面的Nu逐渐增大。虽然雷诺数的提高并没有改变流动的结构,但是蒸汽的流速提高导致近壁面湍流强度增大,从而使Nu升高。

图6 不同雷诺数下带肋底面Nu云图

图7给出了阻力系数f、带肋底面平均努塞尔数Nua、综合换热因子η与雷诺数之间的关系。由图7可见:随着雷诺数的提高,Nua几乎线性提高,f略有增加但幅度很小;Nua的增幅远大于f的增幅。因此,综合换热因子η上升。

图7 不同雷诺数下f、Nua、η曲线

3.3 入口宽高比的影响

在进口截面面积不变的情况下,探究了宽高比W/H对流动与换热特性的影响。W/H分别取1/3、1/2、1/1、2/1、3/1,同时保证雷诺数恒为56 000。

图8给出了不同宽高比下带肋底面的Nu分布云图。由图8可见,随着宽高比增大,带肋底面的Nu增大。这是由于宽高比较小时,高度方向上受到肋片扰动的范围很小,中间主流区域湍流强度几乎没有增大;宽高比较大时,带肋的顶面与底面距离拉近,高度方向上受扰动的范围增大,湍流强度提升,因此带肋底面的Nu呈现出增大的趋势。

图8 不同宽高比下带肋底面Nu云图

图9给出了f、Nua、η与宽高比之间的关系。由图9可见,随着宽高比的增大,Nua上升,f大幅增加。这是因为宽高比增大导致带肋边长占截面周长的比例成倍上升。从总体上看,随着宽高比的增大,Nua相较f增加更快,η单调上升。

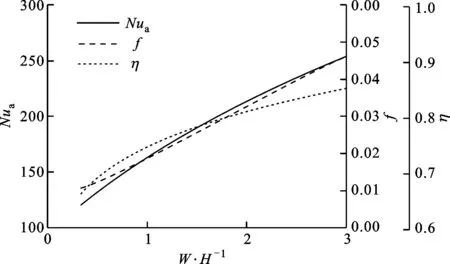
图9 不同宽高比下f、Nua、η曲线

3.4 肋间距的影响

肋间距会改变主流蒸汽的流动结构,从而影响带肋矩形通道的流动和换热特性。维持Re=56 000,改变P使P/e分别为6、8、10、12、14。

图10 不同肋间距下带肋底面Nu云图

图10给出了不同肋间距下带肋底面Nu云图。由图10看见,随着P/e的上升,由入口效应导致的入口换热增强段明显延长,而肋片顶面的高Nu区域则先扩大、后缩小。

当P/e从6增加到12时,相邻肋片底面中间的高Nu区域逐渐扩大,Nu逐渐上升;当P/e=14时,上述区域的Nu比P/e=12时有所减小;当P/e=6时,带肋底面的高Nu区域向左偏移。图11展现了P/e=6时肋顶平面的速度云图,此时高流速区域向下偏移(旋转到对应位置即为向左偏移),这种现象就是“coanda效应”,其导致了带肋底面的高Nu区域向左偏移。图12给出了不同肋间距下yz平面流线图与速度云图。由图12可见:当P/e=6时,虽然肋间存在旋涡,但肋片过密,从而导致主流无法直接冲刷带肋底面,带肋底面附近流速很低,所以Nu很低;随着肋间距增大,更高速的主流取代肋间旋涡直接冲击肋片底面,破坏了换热边界层,因此换热性能增强;当P/e增大到14时,肋片分布过于疏松,对主流的扰动不足以导致湍流强度降低,所以肋间底面Nu下降。

图11 P/e=6时肋顶平面的速度云图

图12 不同肋间距下yz平面流线图与速度云图

如图13所示,随着肋间距的增加,f先增加后减小,η先减小后增加,Nua单调增加。需要指出的是,P/e=14相较P/e=12的情况Nua更高。这是因为肋片前后两侧底面均存在由低速回流造成的低Nu换热“死角”,P/e=14时肋片更少,“死角”占总面积的比值减小,所以Nua略高。

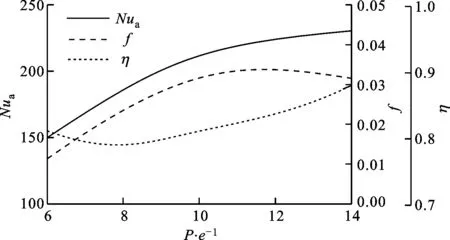
图13 不同肋间距下f、Nua、η曲线

3.5 肋片扰流蒸汽冷却传热关联式

肋片扰流蒸汽冷却传热关联式对于指导冷却叶片设计意义重大。如图7、图9、图13所示,随Re、W/H和P/e的增加,Nua均单调上升。Nua是Re、W/H和P/e的函数,本文假设

Nua=aReb(W/H)c(P/e)d

(3)

拟合了13个数据点,得出传热关联式为

Nua=0.000 34Re0.324(W/H)0.525 3(P/e)1.088 3

(4)

其适用范围为:1.6×104≤Re≤9.6×104,0.33≤W/H≤3,6≤P/e≤14。图14对比了数值计算结果与传热关联式的拟合结果,二者误差在5%以内。传热关联式的计算结果与文献[5]中两组实验(“情况2”和“情况3”)数据进行了对比,计算与实验偏差分别为-38%与-23%。考虑到文献[5]对底面平均Nu的估计比较粗糙,实验仅以约30个测点数据计算了底面平均Nu,且测点大都放置在肋片之间的高Nu区域,使得实验测量值大于真实值。综上所述,传热关联式对于带肋底面传热系数的预测很精确。

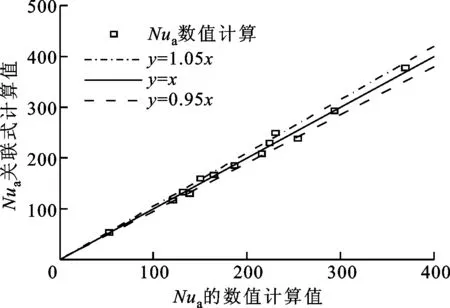
图14 数值计算结果与传热关联式计算结果对比

4 结 论

本文通过求解三维RANS方程和标准k-ω湍流模型,数值分析了带肋矩形通道强化换热的机理,研究了雷诺数、宽高比、肋间距对带肋通道流动阻力与换热特性的影响,主要结论如下。

(1)冷却蒸汽流过带肋矩形通道时,受到肋片的扰动后一方面使肋片附近产生旋涡,另一方面改变了主流的流向并使其直接冲刷带肋底面,两方面作用下带肋底面换热边界层变薄,换热增强。

(2)随着雷诺数的增大,蒸汽在带肋矩形通道中的流动结构并没有发生变化,但流速提高导致湍流强度增大,带肋底面的平均Nu上升,阻力系数小幅增加,综合换热因子单调上升。

(3)随着宽高比的增大,高度方向上被扰动的流体区域增大,带肋底面的平均Nu上升,同时肋片(即通道宽度W)延长,阻力系数大幅上升。因此,综合换热因子呈现增长的趋势。

(4)随着肋间距的增大,蒸汽的流动结构发生了变化,带肋底面的平均Nu单调增加,阻力系数先增后减,综合换热因子先减后增。

(5)肋片扰流蒸汽冷却的传热关联式的计算误差在5%范围内,表明该关联式能够可靠预测肋片扰流冷却的传热系数。

[1] 史晓军, 税琳棋, 高建民, 等. 蒸汽冷却带肋矩形通道传热和压降实验关联式 [J]. 西安交通大学学报, 2013, 47(11): 1-6. SHI Xiaojun, SHUI Linqi, GAO Jianmin, et al. Heat transfer and pressure drop correlations for rectangular channels with ribs [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 1-6.

[2] SHI X, GAO J, XU L, et al. Experimental investigation on heat transfer and friction characteristics of ribbed rectangular channels using steam as coolant [J]. Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy, 2013, 227(4): 426-437.

[3] SHUI L, GAO J, SHI X, et al. Effect of duct aspect ratio on heat transfer and friction in steam-cooled ducts with 60 angled rib turbulators [J]. Experimental Thermal and Fluid Science, 2013, 49: 123-134.

[4] SHUI L, GAO J, XU L, et al. Numerical investigation of heat transfer and flow characteristics in a steam-cooled square ribbed duct [C]∥ASME Turbo Expo 2010: Power for Land, Sea, and Air. New York, USA: ASME, 2010: 163-171.

[5] SHUI L, GAO J, SHI X, et al. The effect of cooling conditions on convective heat transfer and flow in a steam-cooled ribbed duct [J]. Journal of Mechanical Science and Technology, 2014, 28(1): 331-341.

[6] ELWEKEEL F N M, ZHENG Q, ABDALA A M M. Numerical study of turbulent flow through rib-roughened channels with mist injection [C]∥ASME 2014 Turbine Technical Conference and Exposition. New York, USA: ASME, 2014: V05AT12A011.

[7] ZHU J, GAO T, LI J, et al. The effect of vortex core distribution on heat transfer in steam cooling of gas turbine blade internal ribbed channels [C]∥ASME 2014 Turbine Technical Conference and Exposition. New York, USA: ASME, 2014: V05AT12A005.

(编辑 苗凌)

Numerical Simulation for Flow and Heat Transfer Characteristics in Steam-Cooled Square Ribbed Channel

CHEN Yujia,DU Changhe,LI Liang

(Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China)

To clarify the underlying principle of heat transfer enhancement in a steam-cooled square ribbed channel, the flow field and heat transfer characteristics of a square ribbed channel were numerically simulated by 3-D steady RANS equations coupled with standardk-ωturbulence model. The influences of Reynolds number, inlet aspect ratio and rib pitch on the flow and heat transfer characteristics were investigated, the heat transfer correlation of square ribbed channel was analyzed, and then the relationship of Nusselt number with Reynolds number, inlet aspect ratio and rib pitch was obtained. The result indicates that heat transfer enhancement is caused by the existence of ribs which destroy the thick heat transfer boundary layer. As Reynolds number grows up, the average Nusselt number and thermal enhancement factor increase while the friction factor increases slightly. Larger inlet aspect ratio also leads to greater thermal enhancement factor and better average Nusselt number, and the friction factor also increases obviously. The increase of rib pitch results in a growing average Nuusselt number. When the rib pitch increases, the friction factor increases firstly and then decreases, while thermal enhancement factor decreases firstly and then increases.

square ribbed channel; steam cooling; flow and heat transfer; heat transfer correlation; numerical investigation

10.7652/xjtuxb201603010

2015-08-21。 作者简介:陈宇佳(1993—),男,本科生;李亮(通信作者),男,副教授,博士生导师。

时间:2015-12-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20151210.1134.014.html

TK474.7

:A

:0253-987X(2016)03-0062-06