考虑气动和湿汽损失综合影响的低压多级透平优化

李亮,薛太旭,李森

1.西安交通大学能源与动力工程学院,710049,西安;2.西安航天动力技术研究所,710025,西安)



考虑气动和湿汽损失综合影响的低压多级透平优化

李亮1,薛太旭2,李森1

1.西安交通大学能源与动力工程学院,710049,西安;2.西安航天动力技术研究所,710025,西安)

针对叶轮机械多级透平优化的问题,在考虑湿蒸汽透平中气动损失和湿汽损失的综合影响的基础上,采用响应面方法对某300 MW汽轮机低压缸末三级透平进行了优化。优化变量为末三级静叶的安装角和型线沿叶高的积叠规律,安装角优化通过改变多级透平级之间的压力平衡,来改变湿蒸汽透平级内过冷度的分布,降低非平衡热力学损失和水滴的直径,使得末三级的湿汽损失减小了20.71%,由此获得了通过调整低压透平静叶安装角从而减小湿汽损失的方法。静叶积叠规律的优化中通过改善反动度沿叶高的分布、减小叶根边界层分离和降低二次流损失提高了气动效率,同时引起级内过冷度和出口流速沿叶高变化,使一次水滴和二次水滴的直径减小,导致气动损失降低了0.52%,湿汽损失进一步降低了9.48%。该结果可为多级透平优化提供参考。

低压多级透平;气动损失;湿汽损失;响应面方法;优化

火电和核电汽轮机低压缸做功能力大,对整个机组的性能有重要影响。低压缸的末几级透平工作于湿蒸汽区,这样不仅存在气动损失,还存在由于湿蒸汽流动导致的湿汽损失,并对低压透平的性能产生重要影响[1]。

多级透平优化是叶轮机械领域的一个重要研究方向,其中响应面方法取得了很大成功。该方法最早由Box和Wilson提出[2],其特点是在合理选取设计变量的条件下,只需计算较少的样本空间就可以得到比较理想的最优值。Rubechini等用响应面方法对某多级蒸汽透平进行了优化[3],李瑜等也用该方法对某低压七级蒸汽透平进行了优化[4]。然而,这些对蒸汽透平所进行的工作仅考虑了气动损失的影响,而未考虑湿汽损失的影响,因此其优化结果还不能真实反映湿蒸汽透平中的实际流动情况。李瑜等开发的湿汽损失定量计算程序[5],可以对多级蒸汽透平中的湿汽损失进行详细计算。本文基于该程序,在考虑蒸汽透平中气动损失和湿汽损失的综合影响下,对某300 MW汽轮机的低压末三级透平进行了优化。

1 优化策略

低压缸共包含6个透平级,其中末三级工作在湿蒸汽区。为了将优化计算量控制在合理的规模,同时也突出湿汽损失的影响,本文仅对末三级透平的静叶进行了优化。由于低压透平每级静叶均由十几个截面构成,其变量数依然相当可观。因此,本文仅选取末三级静叶的安装角和沿叶高的积叠规律这两组参数作为优化变量。

安装角变化影响叶栅出口面积,引起流速变化并改变各级间的压力平衡,从而起到重新分配各级焓降的目的;各级焓降的改变不仅影响低压透平的气动特性,也会影响湿蒸汽的成核和水滴生长过程,从而对湿汽损失产生影响[1]。各截面叶型沿叶高的积叠规律是控制静叶三维成型的关键参数,对端壁二次流和级的泄漏特性产生影响[3],级内流动特性的改变进一步影响级内的凝结过程,从而改变湿汽损失的大小。

按照上述优化策略,优化过程分为2个步骤,首先对末三级静叶的安装角进行优化,为了考虑多级透平之间的相互影响,气动特性的计算在整缸(六级透平)环境下进行;在此基础上,冻结各级进、出口边界条件,依次对末三级静叶各截面叶型沿叶高的积叠规律进行优化。

2 响应面优化方法

响应面方法通过正交设计确定样本空间,进而建立优化变量与目标函数之间的数理统计关系,其基本步骤包括建立优化变量的响应面,限制变量范围,在响应面上寻找目标函数的极值。优化变量与目标函数之间的关系为[6]

(1)

式中:y是目标函数;xi和xj是优化变量;m是优化变量数;βi是响应面函数系数,由最小二乘法计算;ε为随机误差。

应用响应面方法时忽略样本的随机误差,计算时样本数为(2m+2m+1)。在建立响应面函数后进行显著性检验,如果响应面函数对优化变量的变化不敏感,则需要重新选取样本空间以及重新建立响应面函数关系。目标函数的最大值和相应的优化变量值都是通过响应面获得。

本文中低压透平优化的目标函数为效率,限制条件为流量的变化须小于±0.1%,功率不能减小。

3 求解流动和湿汽损失的数值方法

低压蒸汽透平内的流动采用非平衡凝结流动模型来模拟,其数值方法详见文献[7-8]。在多级透平计算中,动、静叶交接面采用混合平面模型进行参数的传递,收敛标准为每个控制方程的均方根残差小于10-5,且低压透平的进、出口流量偏差小于0.1%。

在获得多级蒸汽透平的三维流动计算结果后,进一步利用文献[5]开发的多级透平湿汽损失的定量计算程序得到各级的湿汽损失。

图1给出了低压六级透平的几何模型,前四级后分别设有4个抽汽口。低压透平计算中给定进口流量、总温、出口背压、各抽汽口的流量和转速。

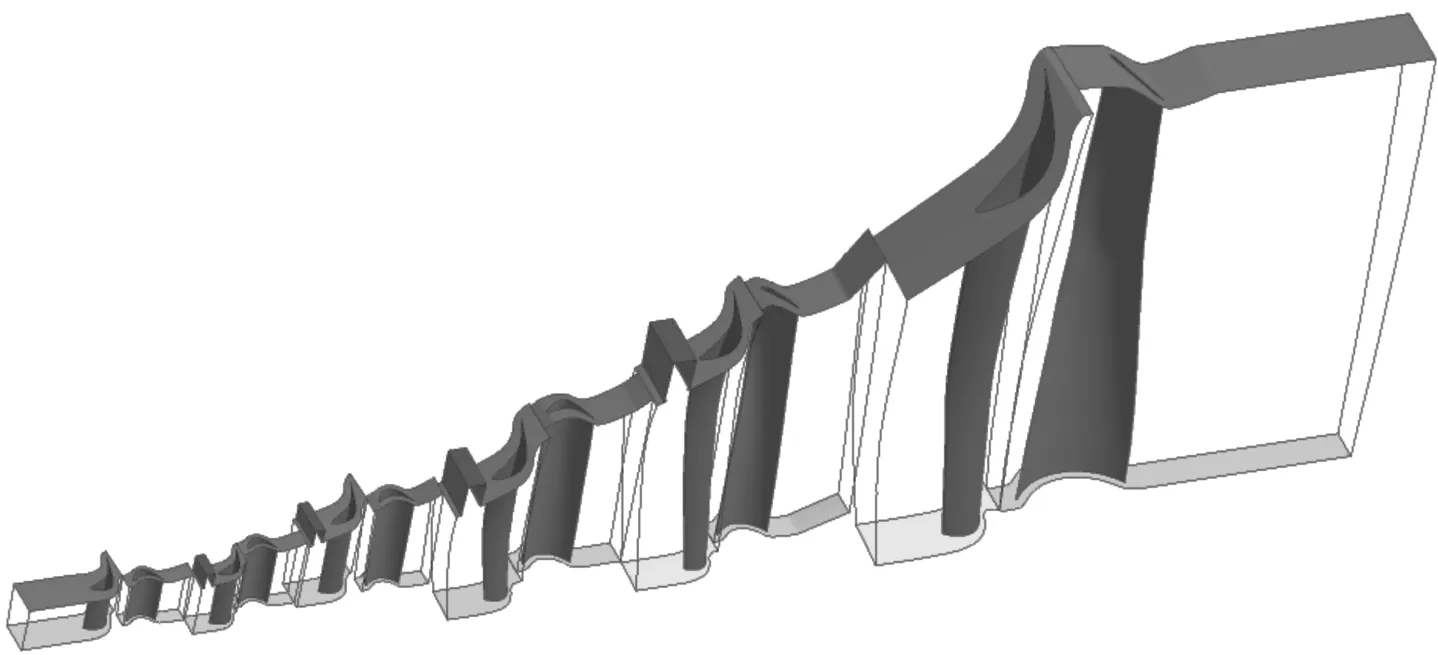
图1 低压透平的几何模型

对于带抽汽口的低压透平,考虑湿汽损失后的效率

(2)

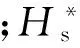
4 低压多级透平优化

4.1 末三级静叶安装角的优化

图2给出了各级静叶安装角旋转方向的定义。在优化末三级静叶安装角时每级静叶均以径向为轴进行整体旋转,允许的旋转角度为-2°～2°,优化变量数为3。建立响应面需要计算15个(23+2×3+1)计算流体动力学(CFD)样本,该样本数按照响应面方法的要求来选取[6]。这些样本数据经最小二乘法计算可以得到功率、流量和效率的响应曲面。图3中仅以效率为例给出了相应的响应曲面。

图2 静叶安装角旋转方向的定义

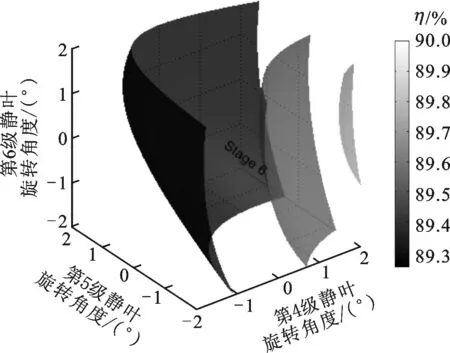
图3 效率对末三级静叶安装角的响应曲面

按照流量变化须小于±0.1%以及功率不能减小的约束条件,得到效率最大时末三级静叶安装角分别旋转1.96°、-2°、0.98°。采用三维数值模拟对上述优化结果进行了验证,结果如表1所示。可以看到,低压透平流量的变化可以忽略,功率和效率均有所提高,湿汽损失降低了20.71%。

图4给出了末三级静叶安装角优化前后各级焓降的变化。可以看到,前二级焓降变化可以忽略,后四级焓降变化较大,第3级和第5级焓降增加明显,第4级焓降减小明显。

表1 末三级静叶安装角优化前后总体性能的变化

图4 末三级静叶安装角优化前后各级焓降变化

4.2 末三级静叶积叠规律的优化

按照本文优化策略,在4.1节优化结果的基础上对末三级静叶各截面叶型沿叶高的积叠规律进行了优化,本文中积叠规律仅涉及弯曲和扭转。图5给出了控制静叶弯曲和扭转的方法。

保持静叶各叶高截面的叶型不变,仅沿周向平移和绕截面型心扭转。固定中截面叶型,将静叶分为上下2个部分。如图5a所示,叶顶截面型线沿周向的相对平移量用a表示,叶根截面的用b表示。从叶顶和叶根到中截面各型线的平移量可以线性或非线性变化,本文选用了较为简单的线性变化规律,这样用2个变量(a,b)即可控制静叶沿叶高的弯曲规律。静叶弯曲规律优化的约束条件定义如下:当a=b=0,即(0,0)代表直叶片、(1,1)代表原始叶片时,a和b允许的变化范围均为-1～3。如图5b所示,静叶各截面型线绕型心的扭转规律采用类似的方法,由变量(c,d)控制,静叶扭转时约束条件的定义方法与静叶弯曲类似,c和d允许的变化范围为-1～3。

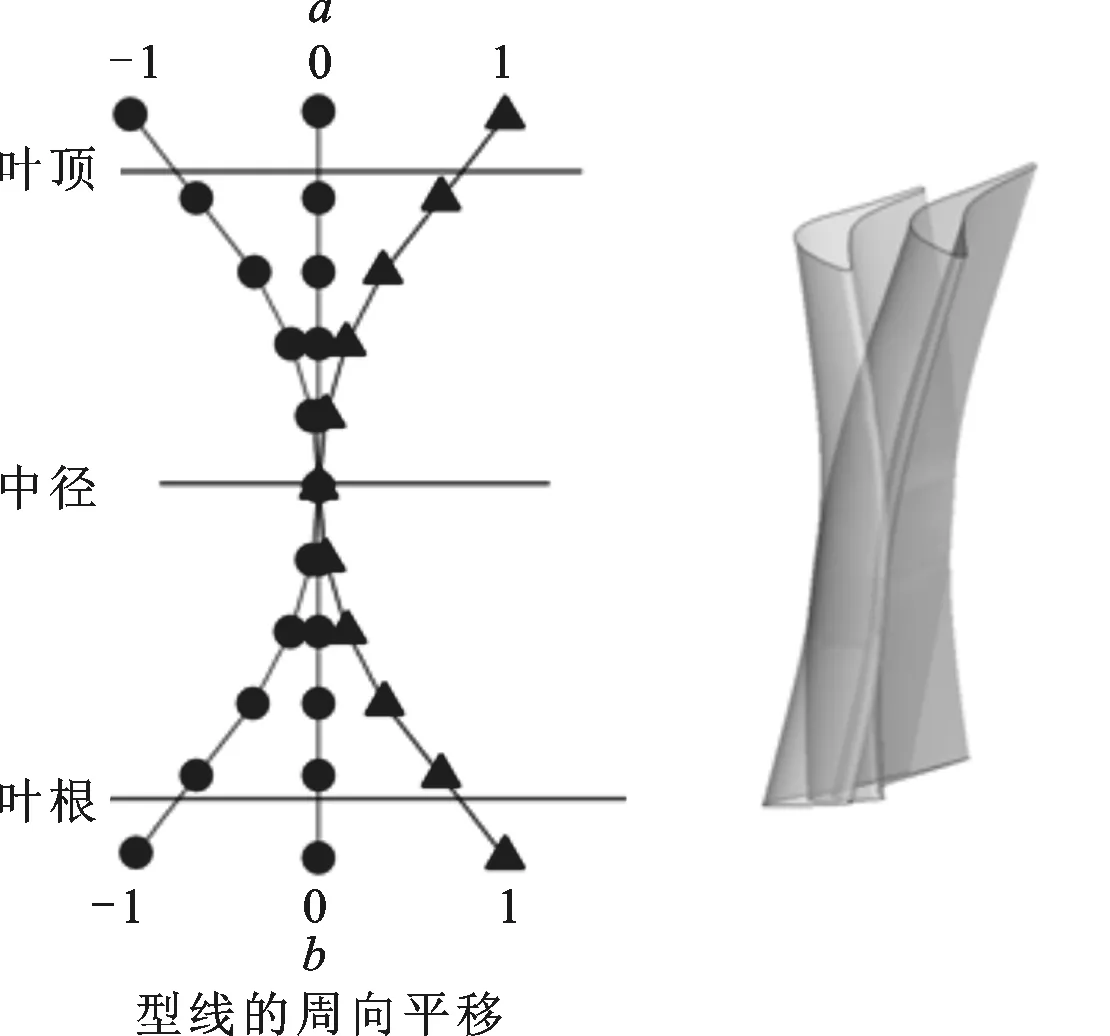
(a)静叶弯曲控制

(b)静叶扭转控制图5 控制静叶弯曲和扭转的方法

在安装角优化结果的基础上,冻结各级进、出口边界条件,依次对末三级静叶的弯曲和扭转规律进行了优化。优化前后静叶的变化如图6所示,其中末级静叶叶型的变化最大。

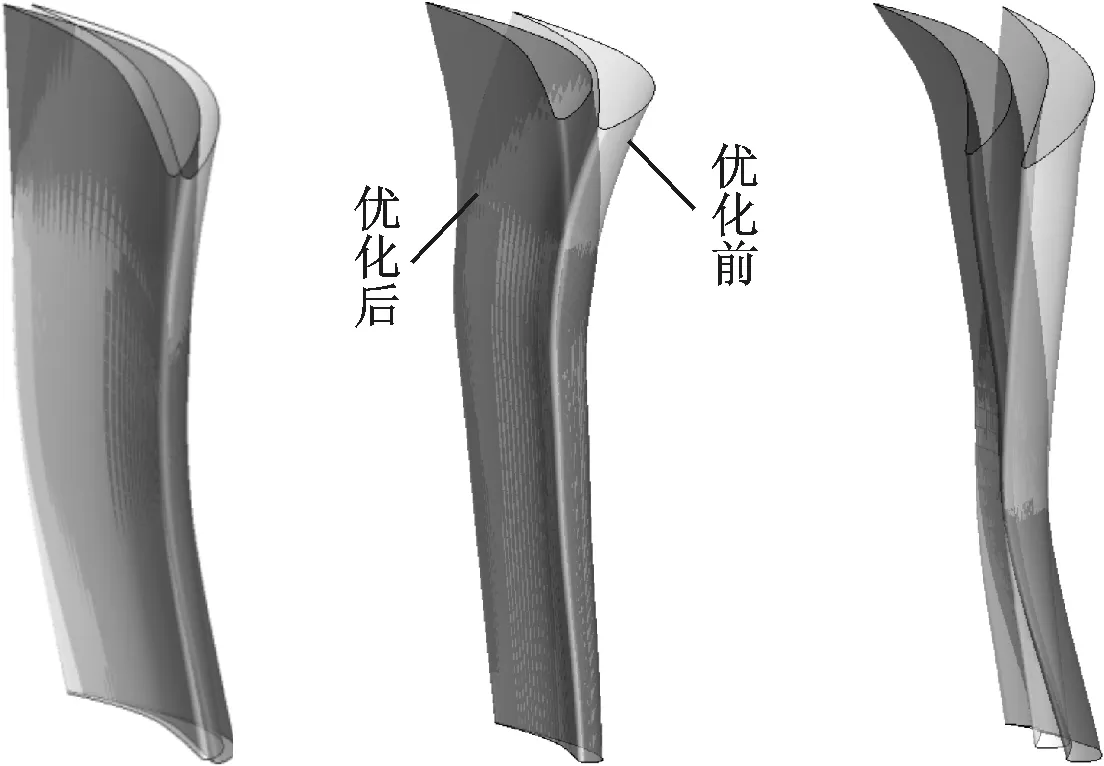
(a)第4级 (b)第5级 (c)第6级图6 优化前后静叶叶型对比

静叶积叠规律优化后低压透平总体性能的变化如表2所示。可以看到,在流量变化可以忽略的条件下,低压透平的功率、效率进一步提高,湿汽损失进一步减小。

表2 静叶优化前后低压透平总体性能参数对比

5 低压透平性能提高的原因分析

由表1看到,改变末三级静叶安装角的主要影响是湿汽损失降低了20.71%,效率和功率的提高基本上是湿汽损失减小的结果。由表2看到,改变静叶各截面叶型沿叶高的积叠规律,不仅使得湿汽损失进一步降低了9.48%,功率和效率也进一步提高了0.6%和0.52%。纯粹气动损失的降低是功率和效率提高的主要原因,这可以从功率和湿汽损失的变化看出,即末三级静叶积叠规律优化后,功率进一步增加了0.41 MW,而湿汽损失仅仅减少了0.05 WM。

在湿蒸汽问题的研究中,设法减少湿蒸汽透平的湿汽损失一直是努力的方向。本文经过2个优化步骤后湿汽损失共降低了30.19%,其降幅相当可观。对于本文优化的低压透平,由于6个透平级中真正工作在湿蒸汽区的仅为末二级,因此湿汽损失减小对低压透平总体性能的提高并不显著。但是,对于核电汽轮机的高压缸,由于透平级均工作在湿蒸汽区,所以降低湿汽损失对高压缸性能的影响相当可观。

5.1 优化安装角降低湿汽损失的原因

改变安装角后多级透平各级间的压力重新进行了平衡,各级内汽流的膨胀率随之改变,从而引起过冷度发生变化。过冷度是湿蒸汽非平衡凝结过程中成核和水滴生长的直接原因[1],因此观察过冷度的变化就能了解湿蒸汽非平衡凝结过程的主要变化特点。

图7给出了安装角优化前后子午面上末三级的过冷度分布。可以看到,在第4级静叶出口处过冷度开始缓慢增加。在安装角优化前的透平中,第4级动叶出口约80%叶高处、第5级静叶沿整个叶高以及在动叶叶顶附近均出现了过冷度为20 K左右的区域,这些位置会发生一次成核,导致热力学损失产生;在末级静叶和动叶出气边也出现了过冷度较高的区域,这些区域会发生二次成核,引起热力学非平衡损失。反观安装角优化后的透平,第4级动叶出口处过冷度仅在10 K以下,不足以引起凝结,因此与优化前透平相比出现湿度的位置会推迟到下一级;第5级静叶的过冷度达到20 K,沿叶高均发生成核;第5级动叶、第6级静叶过冷度较高的区域消失,第6级动叶叶顶附近过冷度较高的区域显著减小。

图7 安装角优化前后末三级过冷度的变化

过冷度的上述变化,一方面直接引起非平衡热力学损失降低,另一方面也后移了凝结发生的位置,缩短了水滴生长的时间,减小了一次水滴和叶栅尾缘二次水滴的平均粒径。这些均是导致级组中湿汽损失减小的原因。要将末三级上述参数的变化一一呈现出来,需要大量的篇幅,因此本节仅给出过冷度的变化,在下节将以末级为例给出液相其他参数的变化。

为了给湿蒸汽透平的设计提供降低湿汽损失的具体操作方法,对比图7所示的过冷度变化情况和图4所示的各级焓降调整情况,可以得到有益的启发。优化前,第5级静叶是发生成核的主要区域,但在第4级动叶出口附近也出现了大范围的高过冷度区域,通过增加第3级(最后1个过热蒸汽透平级)的焓降和减小第4级(第1个湿蒸汽级)的焓降可以消除第4级动叶出口的高过冷度区,使得第4级动叶出口的过冷度缓慢增加。参考图8可知,优化前透平采用冲动式设计,焓降主要发生在静叶,通过增加第5级的焓降,将一次成核限制在第5级静叶,同时消除了该级动叶顶部的高过冷度区域。此外,优化前透平末级也出现了高过冷度区域,通过减小该级焓降,可有效减小高过冷度区域的范围。

优化程序给出的焓降调整策略,无论对火电还是核电的低压缸设计都具有参考价值,该策略可总结为:①增加最后1个过热蒸汽级的焓降,同时降低第1个湿蒸汽级的焓降;②降低末级的焓降,同时增加次末级的焓降;③对于设计完成的机组,仅需调整静叶安装角。核电的高压透平,由于所有透平级均工作于湿蒸汽区,与低压透平显著不同,因此还需要进一步分析。

5.2 静叶积叠规律优化降低气动和湿汽损失的原因

静叶的弯曲和扭转对低压透平的性能有显著影响。静叶积叠规律优化后各级性能参数的变化如表3所示。可以看到,优化后末三级的气动损失和湿汽损失均有不同程度地减小,其中末级效率的提高和湿汽损失的降低最为明显。

表3 静叶积叠规律优化后各级性能参数的变化

由图8还可以看到,优化后末三级反动度均呈现叶顶减小而叶根增加的趋势,反动度沿叶高的变化趋势不仅能改善叶根附近的边界层分离情况,还能有效降低叶栅内沿叶高的压力梯度,从而限制径向二次流的发展,再配合静叶端部扭曲规律的优化,角区二次流也得到了有效抑制。图9以末级静叶为例给出了叶顶角区二次流的抑制情况。级组内边界层分离和二次流损失减少是气动效率提高的原因。本文的几何模型中未包括隔板汽封和叶顶汽封,可以预见,当考虑汽封中漏汽损失影响时,透平效率会进一步提高。

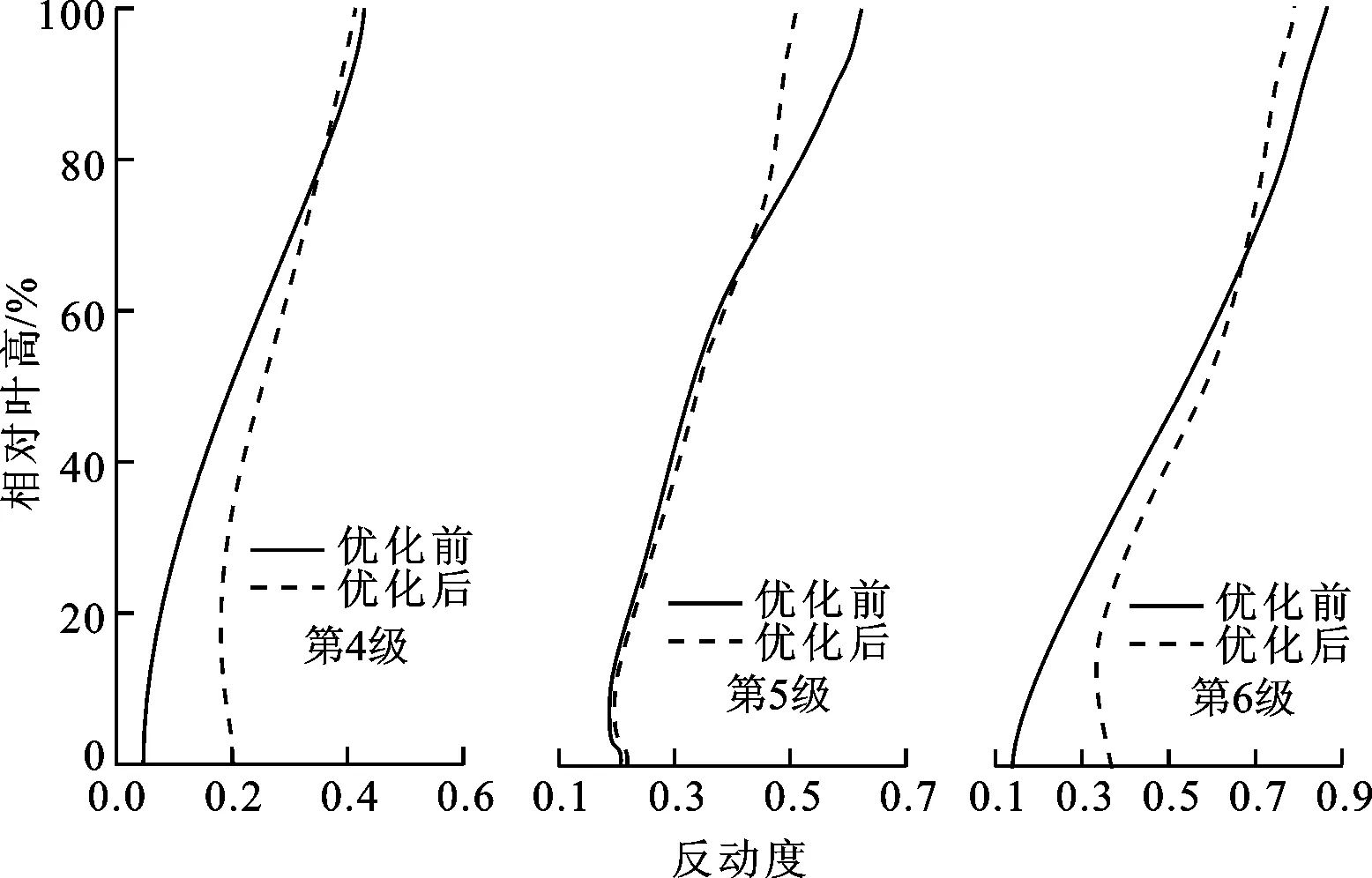
图8 优化前后末三级反动度的变化

图9 优化前后末级静叶叶顶角区二次流的变化

图10和图11以末级为例给出了子午面上一次水滴的直径和叶片尾缘二次水滴的直径。为了对比,同时给出了5.1节中仅对安装角优化后的结果。由图10可以看到,安装角优化后一次水滴的直径明显减小,其最大值从优化前的0.33 μm减小到0.21 μm,而积叠规律的优化进一步减小了一次水滴直径,但减幅较小,表明积叠规律优化仅对级内的过冷度分布起到了局部调整的作用。

图10 优化前后末级中一次水滴直径的分布

图11 优化前后末级静、动叶出气边二次水滴的分布

由图11可以看到,静叶尾缘形成的二次水滴直径在安装角优化后略有增大,动叶尾缘二次水滴直径基本不变。这是由于叶片尾缘二次水滴的大小取决于尾缘处蒸汽的剪切力和水滴表面张力的对比关系的原因[5],安装角优化后末级焓降减小,蒸汽流速、剪切力相应降低,从而造成静叶尾缘二次水滴直径增大。但是,静叶积叠规律优化可以显著改变级内出口气流速度沿叶高的分布,从而显著影响二次水滴的大小。积叠规律优化后静叶尾缘叶顶附近的二次水滴直径明显减小,对于动叶,尽管叶顶附近的二次水滴直径增大,但在小于60%叶高处二次水滴直径均大幅度减小,在叶根附近尤为显著。

积叠规律优化后,一次水滴和二次水滴的直径总体上减小是湿汽损失进一步降低的原因。

图12给出了安装角优化前后各列叶栅出口湿度的变化,静叶弯曲与扭转之后的湿度分布几乎与安装角优化后的重叠,在此不再给出。优化前非平衡凝结从第4级动叶开始,而优化后非平衡凝结从第5级静叶开始,第4级湿度为0,这与图7所示的过冷度变化对应。末二级中,除第5级静叶出口及叶顶附近和第6级静叶出口及叶根附近的湿度分布明显变化以外,其余位置的湿度分布与优化前大体相似。低压透平出口截面的平均湿度由优化前的9.71%增加到优化后的9.90%。

图12 各列叶栅出口湿度沿叶高的分布

图13 优化前后末三级湿汽损失的总体变化

图13和图14给出了优化前后末三级湿汽损失的总体变化和各损失项的详细变化。各项湿汽损失中,热力学损失取决于过冷度的大小,而其他4项的损失均与水滴的大小相关。从图13看到,末三级热力学损失所占比例最大,水滴阻力损失所占比例最小,其他损失所占比例相差不多。优化后,热力学损失降低了6.56%,与图7所示的过冷度变化对应,其他损失均不同程度降低,这是一次水滴和二次水滴直径减小的缘故。从图14看到,优化后第4级的热力学损失基本降为0,第5级的热力学损失略有增大,而末级的热力学损失减小,其余损失均不同程度减小。

图14 优化前后末三级湿汽损失的详细变化

6 结 论

在采用响应面优化方法,以效率为目标,同时考虑气动损失和湿汽损失影响的基础上,对某低压透平进行了优化,结论如下。

(1)通过调整静叶安装角可以调整各级焓降,优化各级过冷度分布,从而达到减小湿汽损失的目的。调整低压透平安装角的策略为:增加最后1个过热蒸汽级的焓降,降低第1个湿蒸汽级的焓降;降低末级的焓降,增加次末级的焓降。本文算例中,在该策略下末三级的湿汽损失降低了20.71%。

(2)通过优化透平级静叶沿叶高的积叠规律,能有效改善反动度沿叶高的分布,减小叶根附件边界层分离,降低二次流损失,提高气动效率,同时也会影响级内的凝结过程和叶片尾缘二次水滴的大小,降低级内的湿汽损失。本文算例中,优化后气动损失降低了0.52%,湿汽损失进一步降低了9.48%。

综合考虑气动损失和湿汽损失的多级透平优化是进一步提高汽轮机效率的一种途径,但由于湿蒸汽流动复杂,所以期待未来通过相关试验测量来验证本文的结论。

[1] MOORE M J, SIEVERDING C H. Two-phase steam flow in turbines and separators [M]. Washington DC, USA: Hemisphere Publishing Corporation, 1976.

[2] BOX G E, WILSON K. On the experimental attainment of optimum conditions [J]. Journal of the Royal Statistical Society: Series B Methodological, 1951,

13(1): 1-45.

[3] RUBECHINI F, SCHNEIDER A, ARNONE A, et al. A redesign strategy to improve the efficiency of a 17-stage steam turbine [J]. ASME Journal of Turbomachinery, 2012, 134(3): 031021.

[4] LI Yu, LI Liang, ZHAO Tong, et al. Aerodynamic optimisation of a low-pressure multistage turbine using the response-surface method [J]. Journal of Mechanical Science and Technology, 2013, 27(8): 2537-2546.

[5] 李瑜, 宁德亮, 李亮, 等. 汽轮机中湿汽损失的定量计算 [J]. 西安交通大学学报, 2014, 48(1): 25-30. LI Yu, NING Deliang, LI Liang, et al. Quantitative evaluation of wetness losses in steam turbine [J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 25-30.

[6] BOX G E, DRAPER N R. Empirical model building and response surfaces [M]. New York, USA: John Wiley & Sons, 1987.

[7] 李瑜, 李亮, 钟刚云, 等. 末级透平对低压缸气动和凝结特性的影响 [J]. 西安交通大学学报, 2012, 46(7): 16-20, 86. LI Yu, LI Liang, ZHONG Gangyun, et al. Influence of last stage turbine on aerodynamic performance and condensation characteristic of low pressure cylinder [J]. Journal of Xi’an Jiaotong University, 2012, 46(7): 16-20, 86.

[8] LI Liang, YANG Jiandao, YOU Wei, et al. Investigation of the vapour-liquid two-phase flow in the low-pressure cylinder of a 1 000 MW nuclear power steam turbine [J]. Journal of Power and Energy, 2014, 228(2): 178-185.

[本刊相关文献链接]

李瑜,李亮,钟刚云,等.末级透平对低压缸气动和凝结特性的影响.2012,46(7):16-20.[doi:10.7652/xjtuxb201207004]

叶冬挺,张荻,蓝吉兵,等.合成射流控制下低压高负荷透平叶片边界层分离大涡模拟.2011,45(3):58-64.[doi:10.7652/xjtuxb201103011]

刘小民,周海洋,王星,等.低压透平叶片表面合成射流非定常流动控制机理研究.2011,45(3):95-101.[doi:10.7652/xjtuxb201103018]

刘小民,周海洋.低压透平叶片流动分离主动控制的数值研究.2010,44(9):21-26.[doi:10.7652/xjtuxb201009005]

蓝吉兵,谢永慧,张荻.采用球窝控制边界层分离流动的大涡模拟.2010,44(9):27-32.[doi:10.7652/xjtuxb201009006]

(编辑 苗凌)

Optimization for Low-Pressure Multi-Stage Turbine Considering Influences of Aerodynamic Losses and Wetness Losses

LI Liang1,XUE Taixu2,LI Sen1

(1. School of Energy and Power Engineering, Xi’an Jiatotong University, Xi’an 710049, China;2. Xi’an Aerospace Propulsion Institute, Xi’an 710025, China)

The last three stages of a low-pressure steam turbine are optimized with the response surface method simultaneously considering the influences of aerodynamic losses and wetness losses. The stagger angles and stacking lines of the last three stages are chosen as the design variables. Adjusting the stagger angles, the pressure distribution, consequently the supercooling distribution, among the multi-stage turbine are changed. As a result, both the non-equilibrium thermodynamic loss and the water droplet diameter are reduced. The wetness losses in the last three stages decrease by 20.71%. The strategy for adjusting stagger angles to reduce the wetness losses is concluded. The optimization of stacking lines improves the radial reaction distribution, reduces the boundary layer separation and secondary losses to heighten aerodynamic effects. Meanwhile the optimization of stacking lines also leads to changes of supercooling and outlet velocity in a turbine stage resulting in decrease in the primary and secondary water droplet sizes. The aerodynamic loss is reduced by 0.52%, and the wetness loss is further reduced by 9.48%.

low-pressure multi-stage turbine; aerodynamic loss; wetness loss; response surface method; optimization

10.7652/xjtuxb201603004

2015-07-14。 作者简介:李亮(1974—),男,博士,副教授,博士生导师。

时间:2015-12-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20151210.1131.010.html

TK262

:A

:0253-987X(2016)03-0022-07