计算气动声学中的伽辽金玻尔兹曼方法研究

邵卫东,李军,2

(1.西安交通大学能源与动力工程学院,710049,西安;2.先进航空发动机协同创新中心,100191,北京)



计算气动声学中的伽辽金玻尔兹曼方法研究

邵卫东1,李军1,2

(1.西安交通大学能源与动力工程学院,710049,西安;2.先进航空发动机协同创新中心,100191,北京)

为获得气动声学的高精度和低耗散特性的数值方法,发展了伽辽金玻尔兹曼方法和相应的无反射边界条件。首先,引入新粒子分布函数到格子玻尔兹曼BGK方程中并重构欧拉方程;然后,在空间上采用高精度的交点间断伽辽金有限元方法,在时间上采用显式五级四阶龙格库塔离散方法对解耦得到的对流步方程进行离散求解;最后,通过数值通量构造速度边界、声学硬壁面边界和无反射边界条件。采用包含声反射和多普勒效应的数值算例进行验证,可得模拟值与解析解吻合一致,从而证明了伽辽金玻尔兹曼方法和无反射边界条件用于气动声学计算的有效性和准确性。

计算气动声学;伽辽金玻尔兹曼方法;无反射边界条件

气动声学问题一般有两类数值解法:基于Lighthill声类比理论[1]及拓展的声比拟预测方法;直接模拟研究噪声的产生机理及传播特性的计算气动声学(CAA)方法。通过计算流体动力学或试验得到流场信息并结合声比拟方法预测噪声在工程中有广泛的应用[2-3],但声比拟方法既不能考虑流场与声场的相互作用,又不能预测非线性气动噪声,故要从更本质的角度研究流动发声机理就必须采用CAA方法。

在CAA中两大关键技术是高精度的时空离散格式和无反射边界条件(NRBC)[4-5]。Tam等提出了色散相关保持差分格式[4],Hu等提出了低耗散低色散龙格库塔格式[6],柳占新等发展了五对角紧致差分格式[7]。这些高阶格式能够显著减少每个波长所需的网格点数,但处理无反射边界时仍需重新构造且精度降低。与Navier-Stokes方程的高阶格式相比,格子玻尔兹曼方法(LBM)[8]具有更低的耗散特性和更快的计算速度,但采用LBM直接模拟[9-10]要有规则的几何和强大的计算资源。邓义求等用LBM研究了点源辐射等声学现象[11],但与NRBC的结合并不理想。Min等将间断伽辽金有限元与LBM结合起来研究了黏性流动而没有考虑其在无黏声传播中的应用[12-13]。

为兼具高精度格式和LBM的优点,本文发展了时空上高精度离散求解无黏速度空间BGK方程的伽辽金玻尔兹曼方法,建立了相应的NRBC,并用声反射和多普勒效应的算例进行了验证。

1 伽辽金玻尔兹曼方法

1.1 无黏速度空间BGK方程

玻尔兹曼方程在离散速度空间下并考虑BGK近似的方程为

α=0,1,…,Nα

(1)

式中:fα为沿格子速度eα=(eαx,eαy)的粒子分布函数;λ为弛豫时间;Nα为离散速度数。本文采用D2Q9模型为

(2)

平衡态粒子分布函数定义为

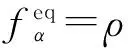
(3)

式中:ρ、u为宏观密度和速度;cs=3-1/2为格子声速;tα为权系数,t0=4/9,t1,2,3,4=1/9,t5,6,7,8=1/36。

对式(1)沿特征线积分有

fα(x+eαΔt,t+Δt)-fα(x,t)=

(4)

对式(4)右端进行积分有

fα(x+eαΔt,t+Δt)-fα(x,t)=

(5)

式中:τ=λ/Δt为归一化弛豫时间;ϑ为隐式所占的比例,本文中取为0.5。

(6)

于是式(5)可重写为

gα(x+eαΔt,t+Δt)-gα(x,t)=

(7)

式(7)的求解又可分为:

碰撞步

(8)

对流步

gα(x+eαΔt,t+Δt)=gα(x,t)

(9)

则宏观物理量密度ρ、速度u=(u,v)、压力p可由粒子分布函数表示为

(10)

(11)

式(9)准确描述了对流过程,但是要求均匀网格和单位CFL数,计算时间长且对不规则几何无法求解。为此,求解可替代的纯对流方程

(12)

1.2 时空离散格式

交点间断伽辽金有限元方法具有局部守恒性和选取数值通量的灵活性,从而获得在一般非规则网格上的高精度并保证波占优问题的稳定性,故对式(12)应用此法求解。

引入通量Gα(g)=eαgα,式(12)变为

(13)

(14)

对式(14)中通量进行分步积分得

-∫Γkφn·Gα(g)dΓ

(15)

式中:Γk为Ωk的边界;n=(nx,ny)为外法向量。

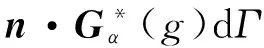
(16)

对式(16)再次分步积分,单元弱形式方程为

(17)

为引入迎风特性,对式(17)右端中数值通量采用Lax-Friedrichs通量,即

(18)

式中:C=max(n·∂G/∂g)=n·eα。

则式(17)右端中数值通量为

(19)

在单元Ωk中定义新粒子分布函数

(20)

采用双线性四边形等参单元将单元内的点(x,y)∈Ωk映射到参考域内的点(ξ,η)∈I=[-1,1]2上。采用高斯GLL积分点的一维拉格朗日插值基函数为

(21)

(22)

N+1个高斯GLL积分点的集合{ξ0,ξ1,…,ξN}是方程(22)的解,则二维张量基可定义为ψij(ξ,η)=li(ξ(x))lj(η(y))。将式(20)代入式(17),并选取试验函数为张量基φ=ψi*j*,则离散弱形式为

(23)

式(23)中的导数项有

(24)

(25)

式(24)、(25)中几何项可逐点计算

(26)

对式(23)采用高斯积分法则,可得单元Ωk上的半离散形式

(27)

式(27)中的每一项有

Mk=(ψij,ψi*j*)Ωk=

(28)

(29)

(30)

(31)

对式(27)两边左乘质量矩阵Mk的逆矩阵,得

(32)

显式五级四阶龙格库塔法[14]的稳定区域和存储空间都优于经典龙格库塔法,对式(32)应用该方法,得

k(i)=aik(i-1)+ΔtL(p(i-1),t+ciΔt),i∈[1,…,5]

p(i)=p(i-1)+bik(i)

(33)

式中:ai、bi、ci为文献优化的常数。

本文取参考长度Lref、速度Vref和密度ρref为10-5m、343.4 m/s和1.2 kg/m3,文中变量均以参考量作归一化处理。

1.3 边界条件的构造

速度边界条件通过数值通量施加,将式(19)简化为

(34)

定义交界面邻近单元的粒子分布函数为

(35)

对于声传播的硬壁面,物理量满足

(36)

式中:u′=(u′,v′)为声粒子速度;p′为声压。

以图1为例,邻近单元的粒子分布函数为

(37)

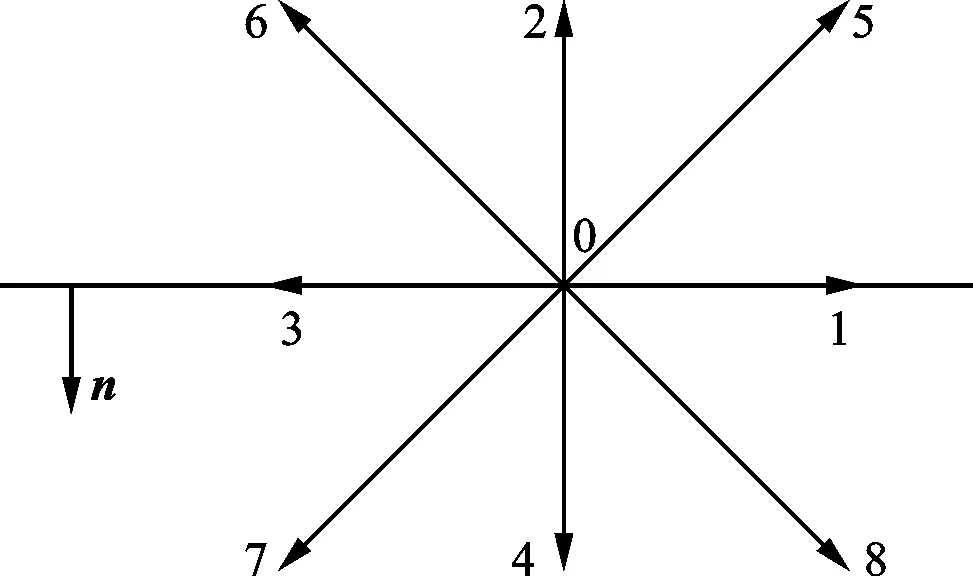
注:0～8表示粒子速度的方向图1 壁面粒子分布函数示意图

根据流体黏性对声的吸收和衰减原理,构造无反射边界条件。考虑沿x轴正方向波数k=2π/Λ和圆频率ω=csk的平面声波从源x=0处开始传播,产生的正弦波的幅值U=csΔρ/ρ0,相应的密度ρ=ρ0+Δρsin(ωt)。上述算例的解析解为

u(x,t)=Uexp(-asx)sin(ωt-kx)

(38)

取x方向足够长和y方向为周期性边界条件,这里取ρ0=1.0,Δρ=0.017 321,Λ=50,υ=10υair=0.044,υair表示空气黏性系数。采用伽辽金玻尔兹曼方法求解上述算例,图2给出了声粒子速度在t=3 000时模拟值和解析解的比较。二者吻合较好,说明了该方法可以模拟声的吸收和衰减作用。

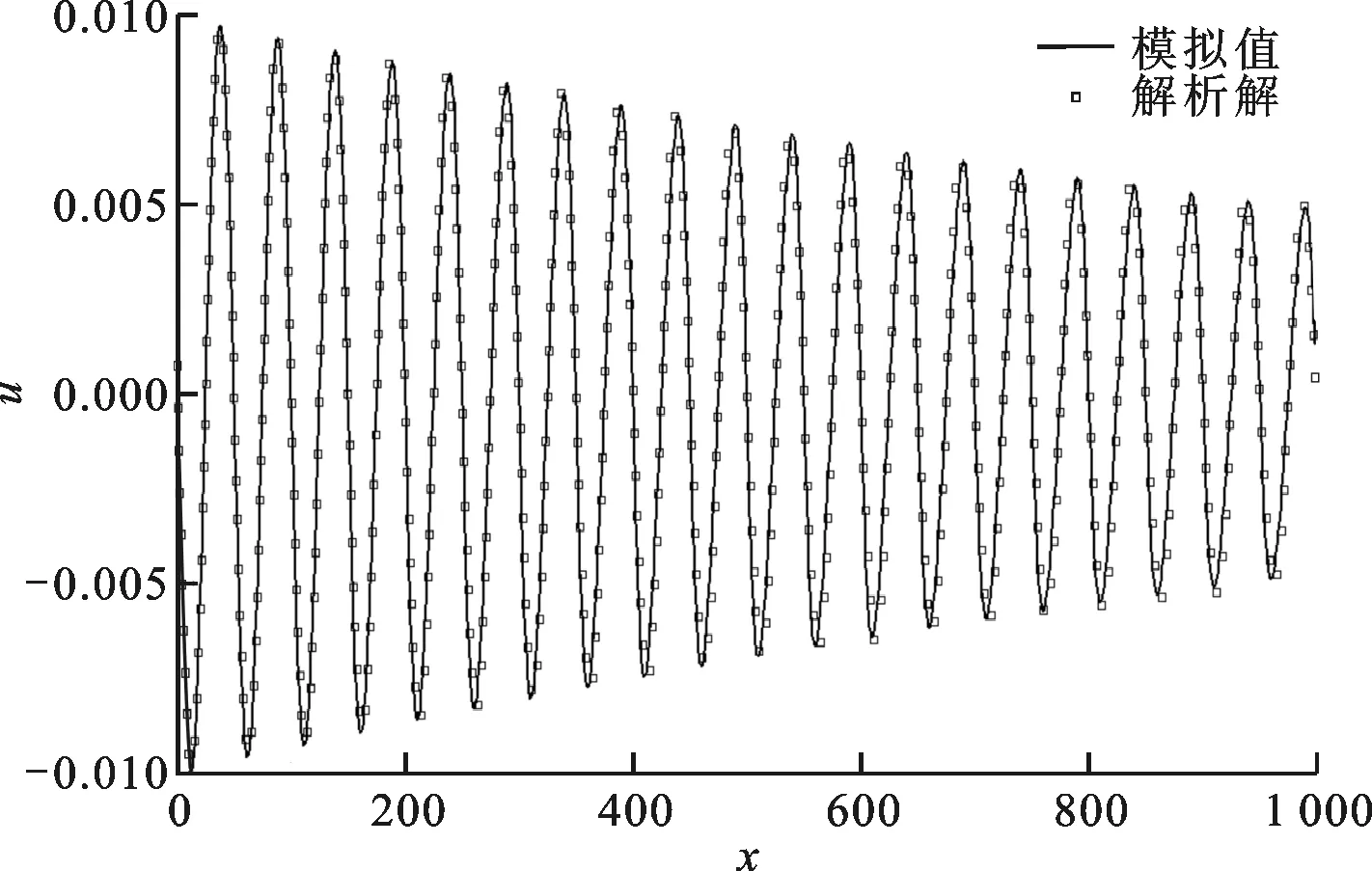
图2 声粒子速度的模拟值与解析解的比较

图3 运动黏性系数对声粒子速度的影响

考察3种不同运动黏性系数25υair、50υair和100υair对声吸收的影响,图3给出了t=3 000时的声粒子速度沿x轴分布。声波沿着传播方向衰减,因此其幅值越来越小。当运动黏性系数增加,声粒子速度幅值减小且衰减较为明显。

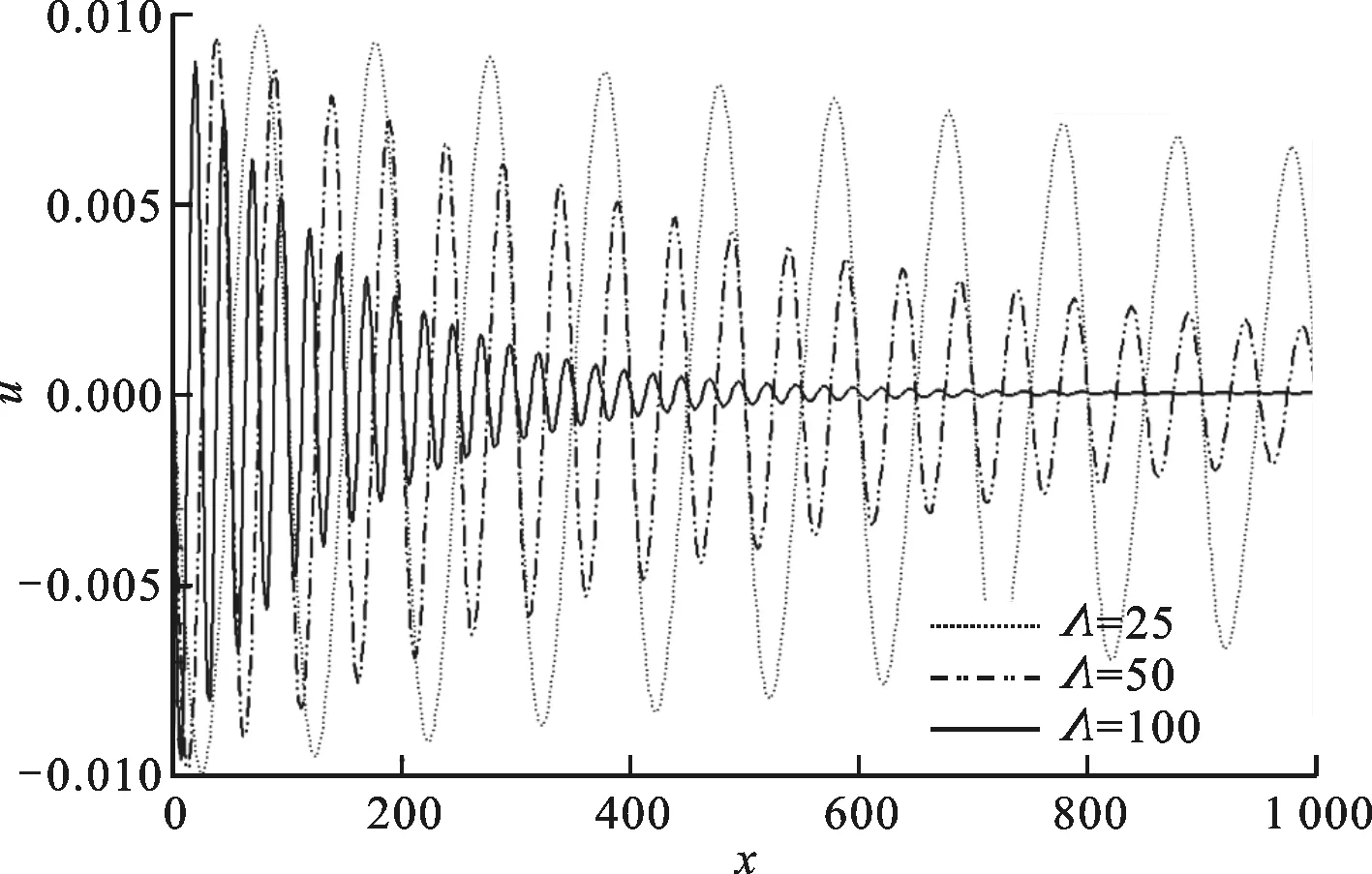
图4 波长对声粒子速度的影响

考察3种不同波长25、50和100在运动黏性系数υ=25υair时对声传播的影响,图4给出了t=3 000时的声粒子速度沿x轴正方向分布。声粒子速度幅值沿着波的传播方向衰减,而随着波长的增加衰减变得缓慢。

由傅里叶级数可知,任意声波可由许多正弦波叠加而成。对声波的衰减可转换为对每一个正弦波的衰减,声粒子速度幅值满足

|u(x,t)|/U=σ

(39)

式中:σ=1%为给定的衰减程度。由式(38)可得,在给定最大波长下衰减声波到给定范围所需的最小距离为

(40)

基于式(40)构造无反射边界条件,为尽可能减小计算域的大小,采用高运动黏性系数来建立高黏性吸声区(HVAZ)。在HVAZ和无黏区(IZ)之间需要添加过渡吸声区(TAZ)来缓和物理量的剧烈变化,从而提高数值计算的稳定性。对于对流步3个区域求解方程相同,而对于碰撞步IZ、TAZ和HVAZ 3个区域弛豫时间对应的黏性系数取为0、2υair和100υair。

2 数值算例与验证

为验证上述方法和边界条件的可行性,本文研究了包含声反射和多普勒效应的算例:初始脉动源在马赫数Ma为0.5的亚声速平均流中与硬壁面相互作用,计算网格如图5所示。初始t=0脉动源为

(41)

式中:xs=0,ys=25为初始源位置;β=ln(2/25)为源形状因子。为了长距离传播而不产生激波,选取源压力脉动幅值ε=0.01,并给出解析解[15]

[J0(ζξ)+J0(ζη)]ζdζ

(42)

(a)脉动声源传播的计算域

(b)脉动声源传播的计算网格图5 脉动声源传播的计算域和网格

HVAZ的边界采用速度边界条件,壁面采用声学硬壁面边界条件,初始粒子分布函数采用麦克斯韦平衡函数。为验证网格的无关性,选取Ma=0.5并使用12 221和17 061个节点来对比4个不同时刻声压的模拟值和解析解。图6给出了两种不同网格数目计算得到的声压与解析解的比较,可知两种网格数目获得的数值解均与解析解吻合一致。采用12 221个节点足够描述该物理现象且该方法能够捕捉声波的变化。随着传播距离的增大,声压的幅值逐渐减小。

图6 沿着直线x=y,s=(x2+y2)1/2的声压分布

图7给出了4个不同时刻的声压分布云图。t=15时刻之前声波各向同性地向四周传播且在t=15时刻几乎到达壁面;在t=45时刻波前撞击壁面而形成反射波;随着时间推进,反射波跟随着原始波传播并在壁面附近相互干涉。随着与壁面距离的增加,声压减弱。两种波在t=75、100时刻都光滑地离开右边界而没有受到HVAZ边界的干扰,证明了NRBC构造的有效性。由于平均流作用,向右传播的波前速度是向左波前速度的3倍。

图7 4个不同时刻的声压分布

图8给出了4个不同时刻计算声压和解析解沿着壁面的分布比较,二者吻合一致,从而证明了声学硬壁面边界条件构造的准确性。在t=15时刻声波刚到达壁面,只能在壁面上形成单波峰且声压值较小;随着时间推移,声波撞击壁面区域变大,故能形成双波峰且声压值较大;在t=75、100时刻右波峰已经传出了右边界。

图8 声压沿着y=0的分布比较

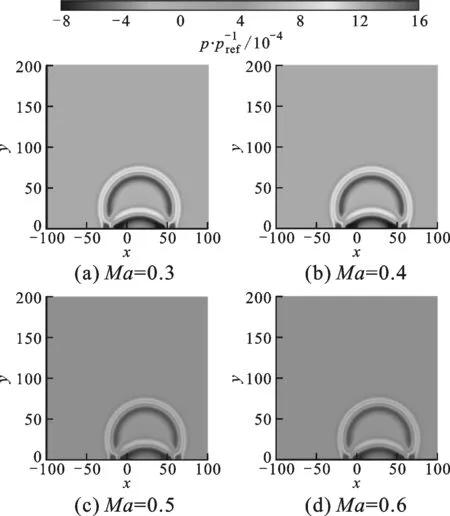
图9 t=45时刻不同马赫数下的声压分布

进一步研究了4种不同马赫数下声波与壁面的干涉情况,图9给出了t=45时刻不同马赫数下的声压分布。仔细观察发现,随着马赫数的增大,左波前向左传播的距离逐渐减小,右波前向右传播的距离逐渐增大,这一现象也可从声波与壁面干涉的位置上发现。尽管声波的位置不同,但声压大小基本一致。

图10 t=45时刻声压沿着y=0的分布

图10给出了不同马赫数下t=45时刻声压沿着y=0的分布,随着马赫数的增大,声压分布整体向右平移。这是由于多普勒效应的作用,声波右行速度为左行速度的(1+Ma)/(1-Ma)倍,与图7中Ma=0.5的结论一致。但是,声压分布的形状并未改变,波峰与波谷之间的距离也没有变化,说明在相对流体的坐标系中声波的传播速度是绝对的,也就是说以声速传播。

3 结 论

本文发展了可用于气动声学计算的伽辽金玻尔兹曼方法。将格子玻尔兹曼BGK方程解耦为碰撞步和对流步,调节运动黏性系数以获得模拟声传播的欧拉方程;对对流步方程应用空间上的交点间断伽辽金有限元方法和时间上的显式五级四阶龙格库塔方法离散求解;通过数值通量构造相应的声学边界条件。

本文研究了包含声反射和多普勒效应的算例,数值解与解析解的良好吻合证明了伽辽金玻尔兹曼方法和边界条件的有效性和准确性。随着声波与源距离的增大,声压幅值减小;随着马赫数增大,多普勒效应显著但声波相对于流体仍以声速传播。

[1] LIGHTHILL M J. On sound generated aerodynamically: I General theory [C]∥Proceedings of the Royal Society of London: A Mathematical, Physical and Engineering Sciences. London, UK: The Royal Society, 1952, 211(1107): 564-587.

[2] 余雷, 宋文萍, 韩忠华, 等. 基于混合RANS/LES方法与FW-H方程的气动声学计算研究 [J]. 航空学报, 2013, 34(8): 1795-1805. YU Lei, SONG Wenping, HAN Zhonghua, et al. Aeroacoustic noise prediction using hybrid RANS/LES method and FW-H equation [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1795-1805.

[3] MAO Y, XU C, QI D. Analytical solution for sound radiated from the rotating point source in uniform subsonic axial flow [J]. Applied Acoustics, 2015, 92: 6-11.

[4] TAM C K W. Computational aeroacoustics: issues and methods [J]. AIAA Journal, 1995, 33(10): 1788-1796.

[5] 李晓东, 旻江, 高军辉. 计算气动声学进展与展望 [J]. 中国科学: 物理学力学天文学, 2014, 44(3): 234-248. LI Xiaodong, MIN Jiang, GAO Junhui. Progress and prospective of computational aeroacoustics [J]. Sci Sin: Phys Mech Astron, 2014, 44(3): 234-248.

[6] HU F Q, HUSSAINI M Y, MANTHEY J L. Low-dissipation and low-dispersion Runge-Kutta schemes for computational acoustics [J]. Journal of Computational Physics, 1996, 124(1): 177-191.

[7] 柳占新, 黄其柏, 胡溧, 等. 计算气动声学中的高精度紧致差分格式研究 [J]. 航空动力学报, 2009, 24(1): 83-90. LIU Zhanxin, HUANG Qibai, HU Li, et al. Study on the high-accuracy compact-finite-difference schemes for computational aeroacoustics [J]. Journal of Aerospace Power, 2009, 24(1): 83-90.

[8] MARIÉ S, RICOT D, SAGAUT P. Comparison between lattice Boltzmann method and Navier-Stokes high order schemes for computational aeroacoustics [J]. Journal of Computational Physics, 2009, 228(4): 1056-1070.

[9] LI X M, LEUNG R C, SO R M. One-step aeroacoustics simulation using lattice Boltzmann method [J]. AIAA Journal, 2006, 44(1): 78-89.

[10]TSUTAHARA M, KATAOKA T, SHIKATA K, et al. New model and scheme for compressible fluids of the finite difference lattice Boltzmann method and direct simulations of aerodynamic sound [J]. Computers & Fluids, 2008, 37(1): 79-89.

[11]邓义求, 唐政, 董宇红. 格子Boltzmann方法应用于气动声学研究 [J]. 计算物理, 2013, 30(6): 808-814. DENG Yiqiu, TANG Zheng, DONG Yuhong. Lattice Boltzmann method for simulating propagating acoustic waves [J]. Chinese Journal of Computational Physics, 2013, 30(6): 808-814.

[12]MIN M, LEE T. A spectral-element discontinuous Galerkin lattice Boltzmann method for nearly incompressible flows [J]. Journal of Computational Physics, 2011, 230(1): 245-259.

[13]ZADEHGOL A, ASHRAFIZAADEH M, MUSAVI S H. A nodal discontinuous Galerkin lattice Boltzmann method for fluid flow problems [J]. Computers & Fluids, 2014, 105: 58-65.

[14]CARPENTER M H, KENNEDY C A. Fourth-order 2N-storage Runge-Kutta schemes [J/OL]. [2015-06-06]. http: ∥www.ece.uvic.ca/～bctill/papers/numacoust/Carpenter_Kennedy_1994.pdf.

[15]HARDIN J C, RISTORCELLI J R, TAM C K W. ICASE/LARC workshop on benchmark problems in computational aeroacoustics [R]. Washington, DC, USA: NASA, 1995: 10-11.

(编辑 赵炜 苗凌)

Study on the Galerkin Boltzmann Method for Computational Aeroacoustics

SHAO Weidong1,LI Jun1,2

(1. School of Energy & Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China)

To get high-accuracy and low dissipative numerical method in aeroacoustics, Galerkin Boltzmann method and corresponding nonreflecting boundary condition (NRBC) were developed. A modified particle distribution function was introduced to lattice Boltzmann BGK equation in order to reconstruct the Euler equation. After decoupling the collision step from the streaming step, we implemented the high-accuracy nodal discontinuous Galerkin spatial discretization and fourth-order, five-stage Runge-Kutta time marching scheme to solve the resulting advection equation. Velocity boundary condition, acoustically hard wall boundary condition and NRBC were constructed through numerical flux. A benchmark problem including acoustic reflection and Doppler effects was used to test the functionality and accuracy of this method and NRBC. Computational results are in good agreement with the analytical solution, implying that it is a promising method for computational aeroacoustics.

computational aeroacoustics; Galerkin Boltzmann method; nonreflecting boundary condition

10.7652/xjtuxb201603021

2015-08-06。 作者简介:邵卫东(1989—),男,博士生;李军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51376144)。

时间:2015-12-28

http:∥www.cnki.net/kcms/detail/61.1069.T.20151228.1956.006.html

V2111 3

:A

:0253-987X(2016)03-0134-07