色噪声激励下非线性随机经济周期模型及其稳定性分析

严惠云,师义民,苏剑,李爽

(1.西北工业大学理学院,710072,西安;2.西安交通大学数学与统计学院,710049,西安;3.西安财经学院统计学院,710100,西安)



色噪声激励下非线性随机经济周期模型及其稳定性分析

严惠云1,师义民1,苏剑2,李爽3

(1.西北工业大学理学院,710072,西安;2.西安交通大学数学与统计学院,710049,西安;3.西安财经学院统计学院,710100,西安)

针对经济变量之间的非线性关系和不确定因素对经济系统的随机干扰问题,根据Goodwin消费函数和Puu函数建立了色噪声激励下的非线性动力学经济周期模型,利用统一色噪声近似原理和等效非线性化方法将模型进行了简化,由此得到了一个等效非线性白噪声模型,以获取判断动力系统稳定性的最大Lyapunov指数。研究结果表明,最大Lyapunov指数与噪声的自相关时间、边际消费率及噪声强度有关。当最大Lyapunov指数的正、负号发生变化时,系统的稳定性也随之改变。若将突发战争、国家宏观经济政策调控等经济系统的外干扰看作色噪声,边际消费作为模型参数,则在边际消费率较小的情况下可以通过加大对经济系统的干预,如国家的经济政策调整等,来稳定经济系统的发展状态。该研究结果可为实现宏观经济的持续增长研究提供参考。

经济周期模型;Gauss色噪声;非线性动力学;Lyapunov指数;边际消费

经济系统是一个复杂系统,其复杂性表现为经济变量之间的非线性关系和不确定因素对系统的随机干扰。非线性动力学方法能准确刻画复杂系统的非线性特性,有效分析复杂系统的演化过程。20世纪30年代法国的物理学家Le Corbeiller提出了利用非线性力学的振动理论来研究经济周期问题[1],自此研究者应用非线性动力学方法从定性到定量对经济问题进行了研究,此后的20年中非线性经济周期模型的研究处于兴盛时期,非线性经济周期模型[2-3]表现出了与线性周期模型完全不同的特征,其极限环[4-6]、Hopf分岔[7]、全局分岔及吸引子[8]、瞬态混沌[9]等复杂的动力学现象引起了学者的研究兴趣,近些年已经从对确定性经济周期模型的研究转化为随机经济周期模型的研究[10-11]。

目前的研究成果中,在对系统的稳定性、分岔和混沌行为进行研究时,外部激励局限于周期扰动或白噪声。白噪声的功率是无限的,事实上真实的噪声具有有限的功率,因此作为外在干扰,白噪声不能描述真实的外激励情况,而具有有限功率的色噪声则更为符合实际情况[12-15]。由于色噪声激励下的随机经济系统具有非常复杂的动力学行为,因此目前还未发现色噪声激励下的随机经济系统的研究成果,现有的成果大多局限于理论研究,实证研究较少,模型的假设与实际情况存在着较大的差异。

鉴于以上情况,本文拟将突发战争、国家宏观经济政策调控等经济系统的外部干扰看作高斯色噪声激励,建立了高斯色噪声激励下的非线性动力学经济周期模型,采用部分线性化方法有效弱化了模型的非线性强度和复杂性,接着应用最大Lyapunov指数研究了该模型的稳定性,最后结合历史数据对模型的稳定性变化做了实证分析,以期能有效分析真实经济系统稳定变化的原因,进而为国家的宏观经济调控决策提供参考依据。

1 经济周期模型及其等效非线性化

1.1 经济周期模型

根据Goodwin的消费函数[4]和Puu的投资函数[16],在参考文献[10]的基础上建立了如下无量纲的经济周期模型

(1)

式中:Q(t)为高斯色噪声,满足

色噪声激励下的模型(1)不是一个马尔可夫过程[17],因此本文利用统一色噪声近似原理[18]将模型(1)简化成一个便于讨论的高斯白噪声激励下的非线性模型。

1.2 模型(1)的噪声白化

根据统一色噪声近似原理,模型(1)可以由白噪声激励下的方程组来近似,即

(2)

式中:Γ(t)为高斯白噪声,满足〈Γ(t)〉=0及〈Γ(t)·Γ(t′)〉=2Dδ(t-t′)。

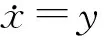
(3)

对式(3)中的第3个等式的两边关于t进行求导,再将求导后的结果带入式(3)的第2个等式中可得模型

(4)

式中:c(y)=-vy3-uy-(1-α)x。

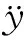
(5)

将式(5)带入式(1)就可得到模型(1)在高斯白噪声激励下的近似经济周期模型

(6)

可以看出,由于γ(y,τ)是y的非线性函数,且出现在模型(6)的分母上,因此模型(6)是一个关于y的强非线性模型,没有办法直接对其计算最大Lyapunov指数。本文考虑将模型(6)部分线性化,得到相应的一个等效非线性模型,从而降低模型(6)的非线性强度和复杂性。

1.3 模型(6)的等效非线性近似

(7)

(8)

为了检验模型(8)的近似精度,在取不同参数值的情况下,计算了模型(6)和模型(8)的数值解,结果如图1～图3所示。

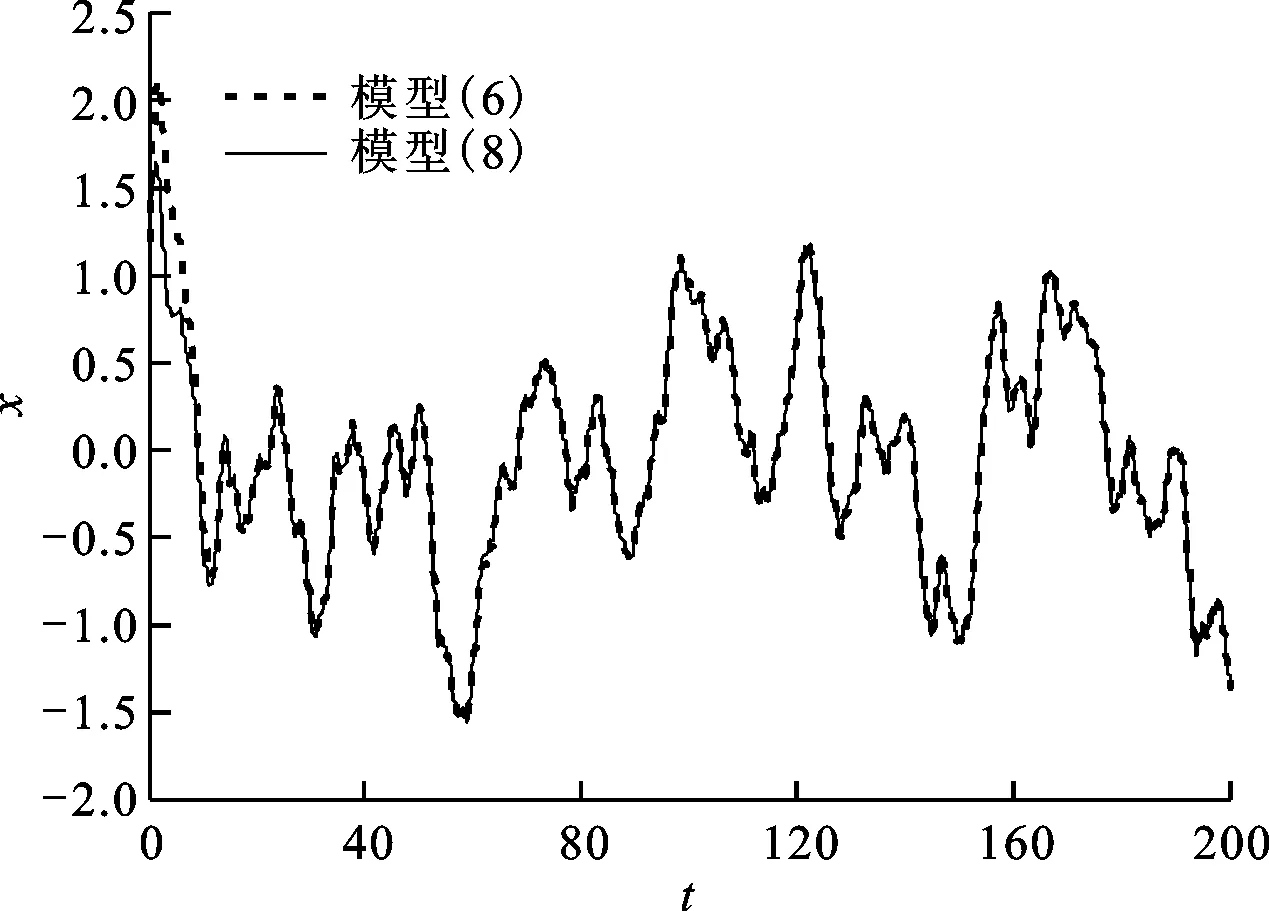
图1 τ=0.25、L=0.2时模型(6)和模型(8)的数值解

图2 τ=0.9、L=0.2时模型(6)和模型(8)的数值解

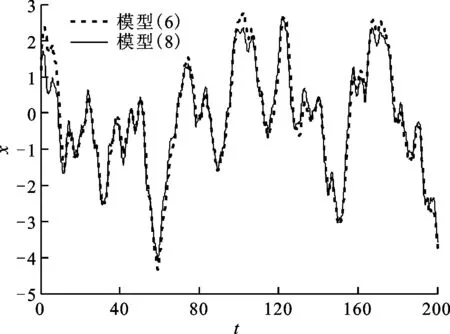
图3 τ=0.5、L=0.9时模型(6)和模型(8)的数值解

由图1～图3可以看出,平衡点(0,0)附近,模型(8)对模型(6)的近似比较理想。因此,下面就以模型(8)来讨论模型(1)在平衡点(0,0)处的稳定性随噪声及参数的变化情况。

2 最大Lyapunov指数的计算

最大Lyapunov指数因为计算简单,通常被用于判断动力系统的稳定性[19]。本文利用拟非可积哈密顿系统的随机平均法[20]计算了模型(8)的最大Lyapunov指数。

(9)

模型(9)的Wong-Zakai修正项为

修正后的模型(9)为

(10)

(11)

则有

因为

所以

由此,可以得到模型(8)的最大Lyapunov指数

(12)

3 经济周期模型稳定变化的实证分析

根据遍历性定理[21],模型(8)表示的经济系统稳定的充分必要条件是最大Lyapunov指数λ<0。从式(12)可以看出,λ是边际消费率α、噪声的自相关时间长度τ及噪声强度L的三元函数。由于λ<0的解析解无法得到,因此将λ的正负号随τ、α及L的变化用蒙特卡洛图表示,如图4～图7所示。

图4 L=0.001时不同τ下λ随着α的变化

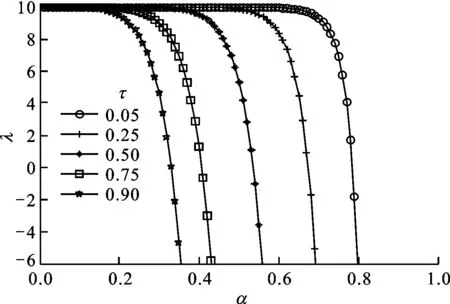
图5 当L=0.01时不同τ下λ随着α的变化

图6 当L=0.1时不同τ下λ随着α的变化

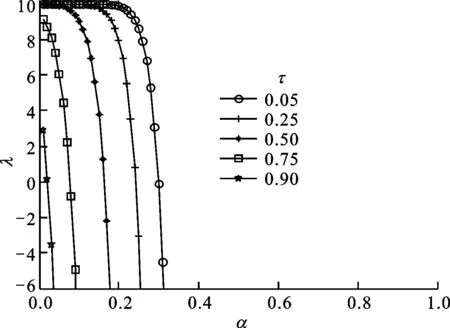
图7 当L=0.5时不同τ下λ随着α的变化

由图4可以得知如下结论。

(1)当经济系统的外激励强度、外激励的自相关时间长度及边际消费率发生变化时,系统的稳定性会随之发生改变。

(2)当L=0.001、α<0.5时,无论τ取何值,λ均大于0。由此可知:当α<0.5时,在外部激励影响很小的情况下,模型(8)定义的经济系统将处于不稳定状态。

当外激励的噪声强度发生变化时,边际消费率及噪声的自相关时间对模型稳定性的影响也会发生变化,对比图4～图7可以得知如下。

(1)在L逐步增大的过程中,经济系统稳定性的内在条件由较大的边际消费率变化到了较小的边际消费率。这正说明,外激励的强度对经济系统稳定性的作用,即在较小的边际消费率的情况下,可以通过加大对经济系统的干预,如国家的经济政策调整等,来稳定经济系统的发展。

(2)噪声的自相关时间长度会影响经济系统的稳定性。在L不变的情况下,噪声的自相关时间越长,系统稳定时的边际消费率就越小。如果将噪声的自相关时间看作是经济干预的周期长度,那么自相关时间越短,干预就越频繁。频繁的经济干预本身就会干扰经济的正常发展,影响经济系统的稳定性,因此建议在实现宏观经济的持续增长期间,国家在对宏观经济调控时应该制定持续有效的经济政策,朝令夕改的经济政策只能让经济的发展更不稳定。

(3)文献[22]测算出中国在1998年的边际消费率为0.375 7(其他年份均大于0.5)。事实上,1997年发生的亚洲金融危机影响到了中国的经济发展,中国1998年的经济发展出现了不稳定现象。为了稳定经济发展,中国政府在1998年实行了积极有力的财政政策和货币政策,促使经济增长率很快得到了提升[23]。这说明本文的实证分析符合中国经济发展的现实情况,验证了该经济周期模型的有效性。

4 结 论

本文采用非线性动力学方法研究了高斯色噪声激励下的经济系统的稳定性,获得的主要结论如下。

(1)在经济系统的平衡点附近,以边际消费率为内因,将其他干扰看作外因,得到色噪声激励下的随机非线性经济周期模型。实证分析表明,边际消费率、噪声自相关时间长度及噪声强度均会影响经济周期模型的稳定性。

(2)当边际消费率小于0.5时,经济系统将出现不稳定性现象,此时政府可以通过宏观政策调控来促进经济的稳定发展,同时所施行的财政政策及货币政策应该比经济平稳发展时期的调整力度大一些,政策调控的频率要小,才能有效的恢复经济的稳定发展。

[1] ICHIMURA S. Toward a general nonlinear macro dynamics theory of economic fluctuations [M]. New Brunswick, NJ, USA: Rutgers University Press, 1954: 192-226.

[2] KALDOR N. A model of the trade cycle [J]. Economy, 1940(50): 78-92.

[3] KALECKI M. A macro dynamic theory of business cycles [J]. Econometrics, 1935(3): 327-344.

[4] GOODWIN R M. The non-linear accelerator and persistence of business cycle [J]. Econometrics, 1951(19): 1-17.

[5] HICKS J R. A contribution to the theory of the trade cycle [M]. Oxford, UK: Oxford University Press, 1950: 56-72.

[6] HICKS J R. Harrod’s dynamic theory [J]. Econometrics, 1949(16): 106-121.

[7] SZYDLOWSKI M, KRAWIEC A. The stability problem in the Kaldor-Kalecki business cycle model Chaos [J]. Solitons and Fractals, 2005, 25(6): 299-305.

[8] AGLIARI A, GARDINI L, PUU T. Some global bifurcations related to the appearance of closed invariant curves [J]. Mathematics and Computers in Simulation, 2005, 68(3), 201-219.

[9] LI Shuang, LI Qian, LI Jiaorui, et al. Chaos prediction and control of Goodwin’s nonlinear accelerator model [J]. Nonlinear Analysis: Real World Applications, 2011, 12(4): 1950-1960

[10]沈菲. 经济系统中的随机分岔与混沌现象研究 [D]. 天津: 天津大学, 2005: 38-78.

[11]李伟, 徐伟, 赵俊峰. 一个经济周期模型的稳定性及其近似计算 [J]. 数学的实践与认识, 2008, 38(12): 120-124.

LI Wei, XU Wei, ZHAO Junfeng. The stability and approximate solution of a business cycle model [J]. Mathematics in Practice and Theory, 2008, 38(12): 120-124.

[12]WANG Nan, SONG Aiguo. Set-reset latch logical operation induced by colored noise [J]. Physics Letters: A, 2014, 378(22/23): 1588-1592.

[13]NAKANISHI T, TSURUHA K. Simulation study of beam extraction from a synchrotron using colored noise with digital filter [J]. Nuclear Instruments and Methods in Physics Research Section: A Accelerators, Spectrometers, Detectors and Associated Equipment, 2009, 608(1): 37-41.

[14]KANG Yanmei, JIANG Yaolin. A semi-analytic method for computing the long-time order parameter dynamics in mean-field coupled overdamped oscillators with colored noises [J]. Physics Letters: A, 2008, 372(46): 6826-6832.

[15]HU D L, HUANG Y, LIU X B. Moment Lyapunov exponent and stochastic stability of binary airfoil driven by non-Gaussian colored noise [J]. Nonlinear Dynamics, 2012, 70(3): 1847-1859.

[16]PUU T, SUSHKO I. A business cycle model with cubic nonlinearity [J]. Chaos, Solitons and Fractals, 2004, 19(3): 597-612.

[17]HUANG Yong, TAO Gang. A feedback control strategy for the airfoil system under non-Gaussian colored noise excitation [J]. An Interdisciplinary Journal of Nonlinear Science, 2014, 24(3): 03311.

[18]JUNG P, HANGGI P. Dynamical systems: a unified colored-noise approximation [J]. Physical Review, 1987, 35(1): 4464-4466.

[19]胡岗. 随机力与非线性系统 [M]. 上海: 上海科技教育出版社, 1994: 197-198.

[20]朱位秋. 非线性随机动力学与控制: Hamiltonian理论体系框架 [M]. 北京: 科学出版社, 2003: 286-295.

[21]OSELEDEC V I. A multiplicative ergodic theorem: Lyapunov characteristic number for dynamical systems [J]. Transaction of Moscow Mathematical Society, 1968, 19(19): 197-231.

[22]YAN Huiyun, SHI Yimin. Nonlinear dynamical analysis and demonstration on Chinese business cycle [J]. Applied Mathematics and Computation, 2011, 218(5): 1547-1552.

[23]王灏. 中国财政货币政策协调研究 [D]. 天津: 南开大学, 2009: 120-149.

(编辑 苗凌)

Stability of Business Cycle Model with a Gauss Colored Noise Excitation

YAN Huiyun1,SHI Yimin1,SU Jian2,LI Shuang3

(1. School of Science, Northwestern Polytechnical University, Xi’an 710072, China;2. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, China;3. School of Statistics, Xi’an University of Finance and Economics, Xi’an 710100, China)

For nonlinear relationships between economic variables and uncertainties to the economic system of random interference problem, a nonlinear dynamical business cycle model with Gauss colored noise is established via Goodwin consumption function and Puu investment function, and the model is simplified with a uniform colored noise approximation theory and equivalent nonlinear method. Furthermore, an equivalent nonlinear white noise model is obtained, then the largest Lyapunov exponents of the determined stability of the economic system is sought out. The approach shows that the largest Lyapunov exponent is related to the correlation time of noise, marginal consumption and noise intensity. The stability of the economic system varies with the change design of Lyapunov exponents. Choosing the sudden war, national macroeconomic policies and economic system interference as Gauss colored noise, and taking the marginal consumption as a model parameter, for the small marginal consumption rate, the economic system development can be stabilized by increasing interventions in the economic system, such as adjustment of national economic policies.

business cycle model; Gauss colored noise; nonlinear stochastic dynamics; Lyapunov exponent; marginal consumption

10.7652/xjtuxb201603022

2015-07-07。 作者简介:严惠云(1977—),女,讲师。 基金项目:全国统计科学研究计划资助项目(2013LY067);陕西省教育厅基金资助项目(2014JK1276);陕西省统计研究中心基金资助项目(14DJ04)。

时间:2015-12-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20151210.1127.002.html

O322

:A

:0253-987X(2016)03-0141-06