燃气透平叶片尾缘开缝结构冷却性能的数值研究
高炎,晏鑫,李军
(西安交通大学叶轮机械研究所,710049,西安)
燃气透平叶片尾缘开缝结构冷却性能的数值研究
高炎,晏鑫,李军
(西安交通大学叶轮机械研究所,710049,西安)
采用包含流体域和固体域的耦合传热数值求解方法,研究了压力侧开缝结构对典型燃气透平叶片尾缘冷却性能的影响,并利用已有的实验数据考核了数值方法的有效性和精度。通过计算获得了不同冷气量、开缝唇厚条件下尾缘部位的冷却性能。结果表明:在所考核的3种涡黏湍流模型中,标准k-ω湍流模型可以较好地模拟叶片尾缘的冷却性能;采用流固耦合传热计算方法可以较好地模拟尾缘开缝出口区域冷却气体的温度分布;增大吹风比可以有效加强内部冷却通道内的对流换热,并增大尾缘开缝出口区域的气膜冷却系数;开缝的高度固定时,唇厚越大,狭缝出口台阶处形成的旋涡尺度增大,减轻了主流流体对狭缝出口壁面的直接冲击,导致狭缝出口区域的总体冷却效果稍微提高,但整体流动损失增大。
尾缘开缝;耦合传热;吹风比;唇厚
现代燃气透平的进口温度远高于叶片材料的熔点,因此需要采用严格的冷却手段来保证叶片的安全性和寿命。为保证机组的气动效率,涡轮叶片的尾缘通常设计得尽可能薄,这就要求尾缘区域必须采用更为有效的冷却措施来避免局部烧蚀[1-2]。在尾缘处通常采用开缝结构进行冷却,即在尾缘压力面侧切除部分结构,使内部冷却通道在此形成一道狭缝,当冷却气体从狭缝内喷出时,会在尾缘区域形成气膜,对高温区进行冷却。为了保证开缝结构的强度并增强冷却通道中的对流换热效果,开缝结构中通常会设置数排肋柱或定位筋等。
目前,国内外已开展了较多关于叶片气膜冷却的研究,但对叶片尾缘气膜冷却性能却关注较少。Taslim等研究了喷射角度、开缝高度、唇厚、吹风比对开缝结构内冷却性能的影响[3],发现开缝高度、唇厚及吹风比对尾缘区域冷却有很大影响,喷射角度的变化影响不大。Holloway等对尾缘开缝结构进行了实验和数值研究[4],研究表明开缝出口流场具有明显的周期性和非定常特性。Ames等对带尾缘开缝结构的叶片进行了实验研究[5-6],分析了带多排圆形肋柱的尾缘开缝结构对叶片内流场及冷却效果的影响。Martini等对冷却通道内肋柱的形状和布置进行了一系列的实验和数值研究[7-9],比较不同肋柱结构对冷却效果的影响。随后,Effendy等在文献[2]实验研究的基础上对叶片尾缘吸力面主流的影响进行了详细的数值研究[10]。国内的徐虹艳等在叶片尾缘内部以射流孔和旋流腔代替肋柱,来研究旋流腔室对叶片尾缘冷却效果的影响[11]。周超等对二维涡轮叶片尾缘开缝结构在跨声速条件下的冷却性能进行了数值研究[12],发现冷却气流在开缝出口后的区域具有明显的脱离再附着现象,壁面温度呈现先增大后减小的趋势。王掩刚等对尾缘开缝喷气与主流的掺混及干扰作用进行了一系列的实验及数值研究,分析了开缝结构对叶片尾缘区域流场的影响[13-14]。
上述对尾缘开缝结构内冷却性能的数值研究中,均采用给定恒定壁温、单纯采用流体域的方法进行流动传热特性计算,这种简化且没有考虑固体与流体之间的相互传热作用,会对冷却系数的计算结果产生很大影响。本文在Martini等实验研究的基础上,利用商用计算流体动力学软件ANSYS-CFX,采用包含流体域、固体域的热流耦合数值求解方法,研究了尾缘开缝结构对动叶尾缘区域内冷却性能的影响。
1 计算模型和数值方法
图1、2分别给出了尾缘开缝结构与本文数值计算模型,表1给出了尾缘开缝结构的主要几何参数。由于实验中狭缝出口后的固体近似为绝热材料,因此本文数值计算时设置开缝出口后的固体表面为绝热壁面。定义狭缝出口在x方向坐标为0,绝热壁面在x、z方向的长度L3、s分别为40、24 mm,分别对应x/H为0~10和z/H为0~6。表2给出了本文数值计算边界条件。计算时出口静压为105.5 kPa,与实验条件保持一致,工质采用理想空气。
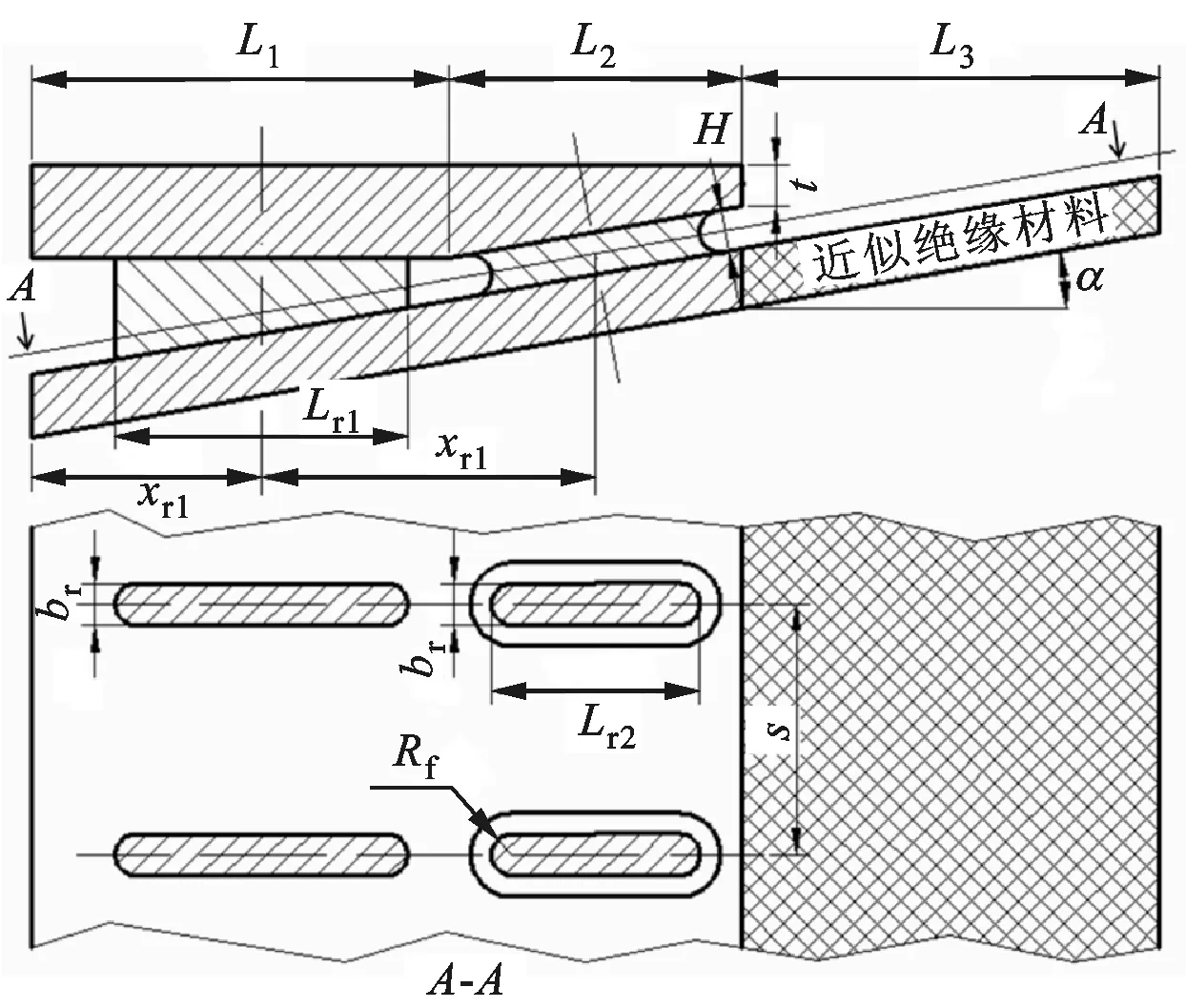
图1 尾缘开缝结构

图2 数值计算模型
图3给出了本文数值计算网格,计算网格采用ANSYS-ICEM生成的多块结构化网格。为了提高网格质量,两个肋柱壁面附近均采用O型网格。
计算时,流体域边界与固体域边界设置为流固交接面,两个界面之间进行热量传递时保证热通量守恒,温度传递时采用插值传递的方式。当动量与质量方程的均方根残差小于10-5、能量方程的均方根残差小于10-6时,计算结果收敛。

表1 尾缘开缝结构主要几何参数
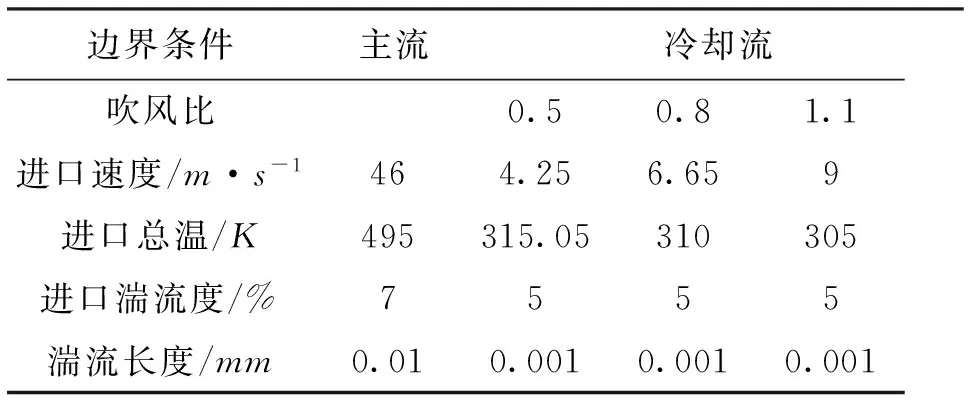
表2 数值计算的边界条件

图3 本文数值计算网格
对控制方程的空间离散采用有限体积法。湍流模型采用标准k-ω两方程湍流模型,计算离散精度为二阶。
本文中吹风比定义为
M=ρcuc/(ρhguhg)
(1)
式中:ρc、ρhg为冷却气体和主流流体进口处的密度;uc、uhg为冷却气体和主流流体进口处的速度。
绝热冷却效率定义为
ηaw=(Thg-Taw)/(Thg-Tc)
(2)
式中:Taw为绝热材料壁面的温度;Thg、Tc为主流高温流体和冷却气体进口处的温度。
能量损失系数定义为
(3)
式中:Ps2、Pt2为出口静压和总压;Pt1、Ptc为主流流体和冷却气体进口总压;mhg、mc为主流流体与冷却气体的流量;Tt1、Ttc为主流流体和冷却气体的进口总温;k为比热容。
主流总压损失系数定义为
φ=2(Pt1-Pt2)/(ρu2)
(4)
式中:u为出口气流平均速度。
2 结果分析
2.1 冷却通道的流量系数和流场结构
本文冷却通道中的流量系数定义为
(2k/(k-1)RTtc[(Ptc/P3)k-1/k-1])1/2}
(5)
式中:P3为狭缝出口的静压;A3为狭缝出口的面积;R为气体常数。
图4给出了冷却通道内流量系数与吹风比的关系。采用k-ω和SSTk-ω湍流模型计算得到的流量系数与实验结果吻合良好,偏小3%左右,而采用k-ε湍流模型计算得到的流量系数比实验值偏大10%左右。
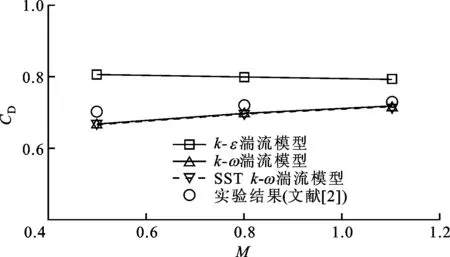
图4 冷却通道内流量系数与吹风比的关系

图5 肋2表面静压孔位置及压力比的分布
图5给出了肋2表面静压孔位置及压力比的分布,从图中可以看出,采用k-ω和SSTk-ω湍流模型计算得到的静压孔位置x1、x2、x3、x4处的压力比Pi/Ptot,L1基本一致,均与实验值吻合良好,而采用k-ε湍流模型计算得到的压力比值比实验值大。由此可见:采用k-ω和SSTk-ω湍流模型比采用k-ε湍流模型计算得到的冷却通道流量系数和肋2表面压力分布结果与实验值吻合得更好。
图6给出了能量损失系数及主流总压损失系数与吹风比的关系。从图中可以看到,主流总压损失系数随着吹风比的增大而逐渐减小,总体能量损失系数基本保持不变。吹风比增大时,冷却气体与主流流体的速度差减小,掺混过程中的流动损失减小,因此主流总压损失系数降低,而吹风比增大又会使冷却通道内的流动损失增大,综合作用下得到的总体能量损失系数基本保持不变。实际设计时,过大的吹风比会对叶片尾迹流动产生很大干扰,降低下级叶栅进口温度,影响透平级效率,因此需要根据具体工况确定合适的吹风比。
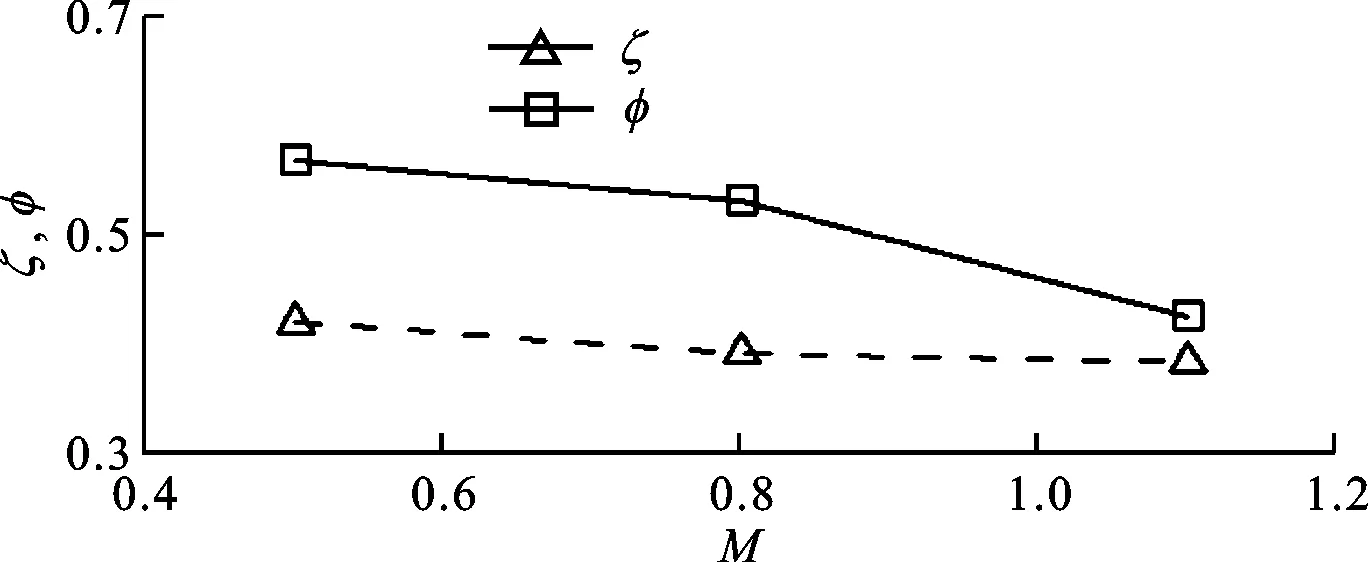
图6 损失系数与吹风比的关系
2.2 网格无关性验证
分别采用100万、200万、400万和800万的流体域网格来研究网格疏密对绝热壁面冷却效率分布的影响。图7给出了不同网格数时,绝热壁面展向平均冷却效率的分布。从图中可以看出,在相同的吹风比条件下,采用网格数为200万、400万、800万的流体域网格计算得到的绝热壁面冷却效率分布基本一致,最终本文采用400万的流体域网格对尾缘狭缝内的流动传热特性进行研究。
2.3 数值方法的验证
图8给出了采用不同湍流模型时,绝热壁面展向平均冷却效率分布。在x/H为0~4之间的区域,采用k-ε、k-ω和SSTk-ω这3种湍流模型计算得到的绝热壁面展向平均冷却效率变化规律与实验结果规律一致,均是随着x/H的增大而逐渐增大;在x/H>4时,实验得到的绝热壁面冷却效率逐渐下降,而数值计算结果仍然保持缓慢增长的趋势,比实验值偏高。总体来看,3种湍流模型中采用k-ω湍流模型的计算结果与实验值吻合较好,与文献[2]的数值计算结果最接近,准确度也高于文献[10]的数值计算结果。
从图8中可以看到,采用RANS方法计算得到的绝热壁面冷却效率分布规律均与本文计算结果一致。采用RANS方法求解时得到的绝热壁面下游区域的冷却效率相比实验结果偏高,这是由于狭缝出口区域具有周期性旋涡脱落的非定常流动特性[4],如果要对该区域的冷却效率进行更加准确的预测,则需要使用更加精确的模型,如DES,LES等。
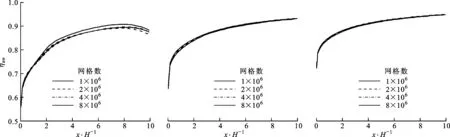
(a)M=0.5 (b)M=0.8 (c)M=1.1图7 不同网格密度得到的绝热壁面展向平均冷却效率分布

(a)M=0.5 (b)M=0.8 (c)M=1.1图8 不同湍流模型得到的绝热壁面展向平均冷却效率分布
2.4 耦合传热与纯流体域计算结果比较
图9给出了采用耦合传热计算方法与采用流体域计算方法计算得到的绝热壁面展向平均冷却效率分布。采用流体域计算时,设置所有固定壁面温度为380 K[10]。本文采用纯流体域方法计算得到的绝热壁面展向平均冷却效率分布与文献[10]的数值计算结果基本一致,与文献[2]的数值计算结果相比总体偏低,与采用耦合传热计算方法得到的结果相比在M=0.5时总体较高,在M=0.8、1.1时总体较低。在M=0.8、1.1时,采用耦合传热计算方法得到的绝热壁面展向平均冷却效率与文献[2]的数值计算结果十分接近,并且与实验值吻合更好。
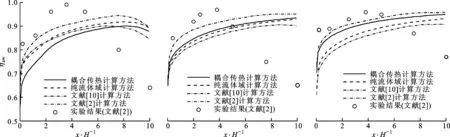
(a)M=0.5 (b)M=0.8 (c)M=1.1图9 不同计算方法得到的绝热壁面展向平均冷却效率分布
图10给出了采用两种计算方法得到的子午面(z/H=3)固体及流体温度分布。采用耦合传热计算方法得到结果中,与主流流体接触的固体表面温度明显高于400 K,因此采用流体域计算时,设置壁面温度为380 K会使计算得到的主流近壁面区域温度较低,主流在开缝出口处与冷却气体的掺混温度也较低。耦合传热计算方法得到的结果中显示,吹风比增大使得固体内平均温度显著降低,说明增大吹风比对固体的冷却效果十分明显。在3种吹风比条件下,耦合传热计算方法得到的肋柱表面的平均温度分别在400 K,380 K和370 K左右,计算得到的冷却气体的温度相比于纯流体域计算结果在M=0.5时整体较高,在M=0.8时基本一致;在M=1.1时整体较低。冷却气体温度分布与肋柱温度分布规律相一致,冷却通道内固体表面温度对冷却气体温度分布有很大影响。加入固体域进行耦合传热计算时,固体表面的温度分布与采用流体域计算时设定的恒定壁温条件相差很大,对主流流体和冷却气体温度分布计算结果均有明显影响。
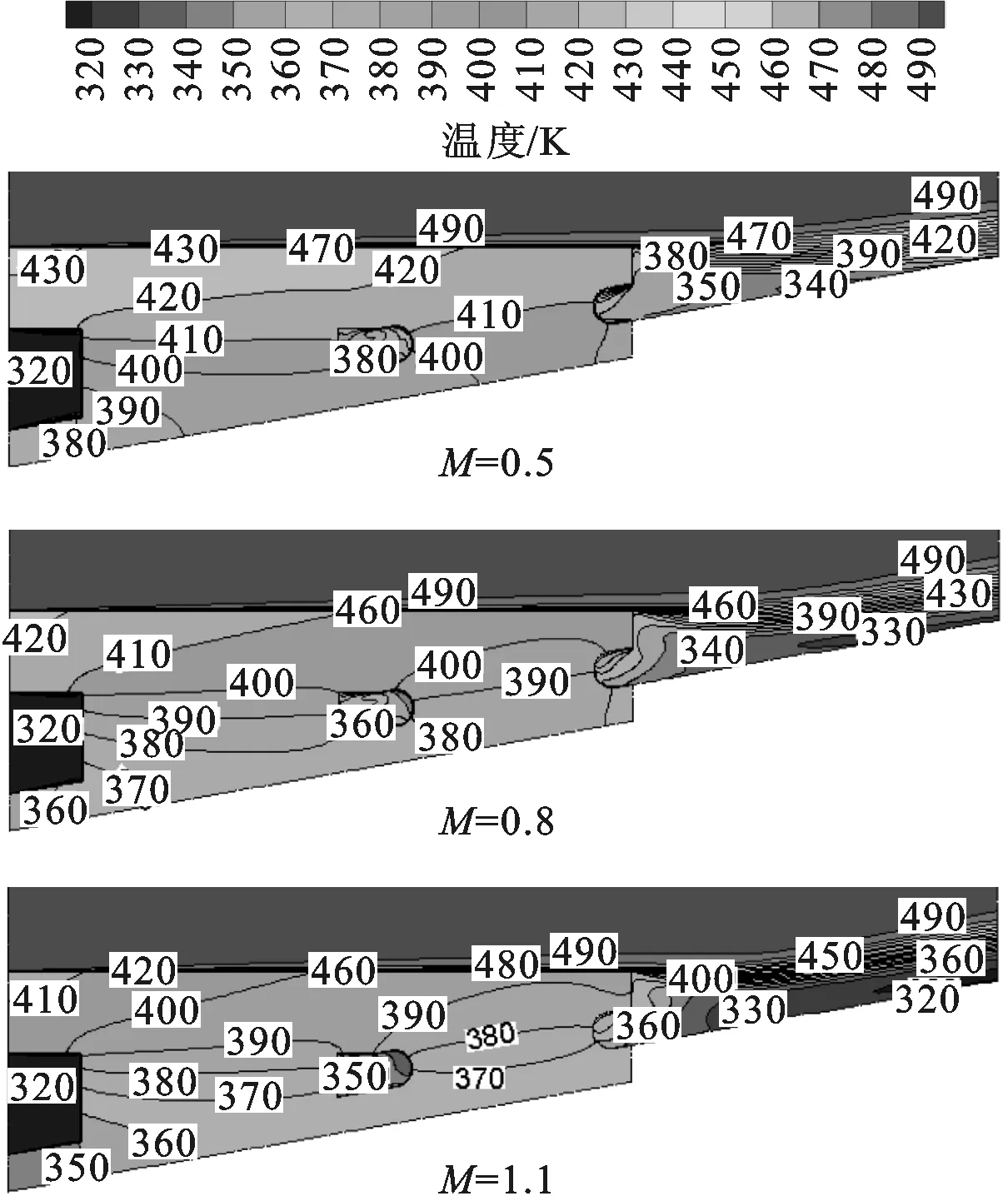
(a)耦合传热计算结果

(b)纯流体域计算结果图10 子午面固体及流体温度分布
图11给出了吹风比为0.8时,z/H=1截面上温度比(T/Thg)的分布。冷却气体对绝热壁面上游区域温度的影响,主要是通过冷却气体在冷却通道下壁面附近存在的热边界层的作用。冷却气体在冷却通道内被加热,呈现出两侧近壁面温度高、中间温度低(与进口温度相差不大)的分布规律。冷却气体在通过狭缝出口时,绝热壁面附近气体仍具有较高的温度,在流动过程中近壁面气体温度逐渐降低。因此,在1点处绝热壁面温度Tw1最高,冷却效率较低,沿着流动方向冷却效率逐渐增大。在5点附近区域的气流温度最低,存在冷却效率的最大值。在6点位置以后,主流高温气体开始作用到绝热壁面,使绝热壁面温度持续增大,冷却效率下降。

图11 z/H=1截面温度比(T/Thg)分布
图12给出了两种计算方法得到的绝热壁面冷却效率分布。采用纯流体域计算时,由于壁面温度均设置恒定,在不同吹风比条件下形成的热边界层相差不大,因此绝热壁面冷却效率分布基本一致。采用耦合传热计算方法时,随着吹风比的增大,固体温度逐渐降低,所形成的热边界层温度逐渐降低,作用距离缩短,因此在狭缝出口处绝热壁面的冷却效率逐渐增大,低冷却效率区域逐渐减小,高冷却效率区域逐渐增大并向绝热壁面上游移动。
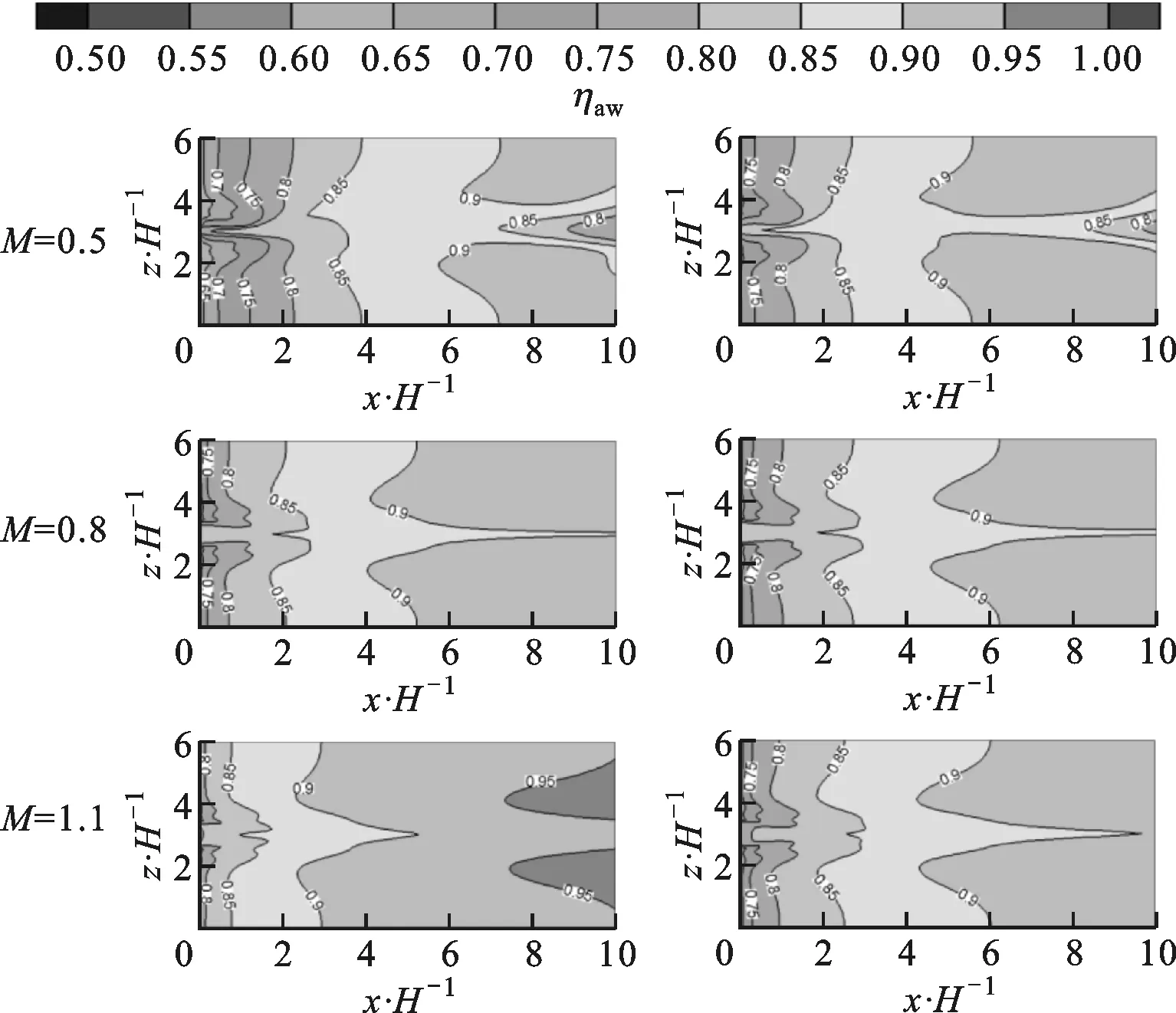
(a)耦合传热计算 (b)纯流体域计算图12 绝热壁面冷却效率分布
热边界层只存在于偏离肋柱即z/H为0~2和z/H为4~6之间的区域,主要是这些区域冷却气流具有比较明显的层流流动,而在z/H为2~4之间的区域由于肋柱的作用而存在十分复杂涡系结构,流动换热情况比较复杂。在肋柱背风面低压的作用下,冷却气体流经肋柱后存在一个向中间偏转并加速的过程,造成等冷却效率线沿流动方向存在两处明显的突出。部分偏转气体会在x/H为2左右的区域形成旋涡,并带动一部分气体反向流向肋柱,因此在z/H为2.5~3.5、x/H为0~2之间区域的冷却效率与x/H为2附近的冷却效率基本一致,等冷却效率线存在一个与流动方向相反的突出。在z/H为2.5~3.5之间区域,受肋柱背风面低压的影响,主流流体会更快地作用到绝热壁面上。从图10可以看到,随着吹风比的增大,绝热壁面z/H为2.5~3.5之间的下游区域冷却效率显著增大。吹风比增大,使得冷却气体的流速提高,可以有效减轻主流流体对绝热壁面直接冲击,改善绝热壁面上的气膜冷却效果。
综上,冷却气体温度分布尤其是绝热壁面上游热边界层的温度分布,对绝热壁面冷却效率的分布有很大影响。只有采用包含固体域和流体域的耦合传热计算方法,考虑流体与固体之间的耦合传热作用,才能更好地模拟狭缝出口区域冷却气体的温度场以及绝热壁面的冷却效率分布。
2.5 唇厚对绝热壁面冷却效果的影响
采用k-ω湍流模型及耦合传热方法研究不同开缝唇厚(t/H=0.25,0.5,1,1.5)对尾缘开缝结构出口绝热壁面冷却效果的影响。图13给出了吹风比为0.8、不同唇厚时,绝热壁面展向平均冷却效率的分布。
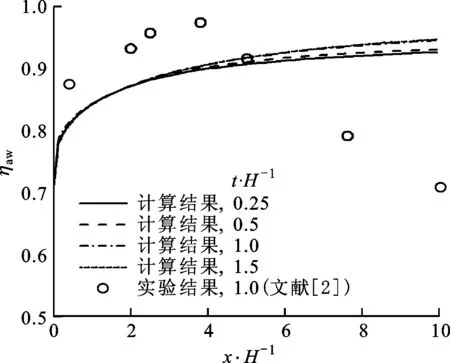
图13 绝热壁面展向平均冷却效率分布
在x/H为0~3的区域,不同唇厚时,绝热壁面展向平均冷却效率基本一致,在x/H>3的区域,t/H增大时冷却效率稍微增大。t/H为1和1.5时,得到的冷却效率相差很小。说明适当增大唇厚可以改善狭缝出口区域冷却效果,但是唇厚增大到一定程度时,冷却效果不再有效改善。
图14给出了吹风比为0.8,不同唇厚时,绝热壁面上的冷却效率的分布情况。唇厚对绝热壁面冷却效率的影响主要集中在z/H为2.5~3.5之间区域,其他区域的冷却效率分布基本一致。
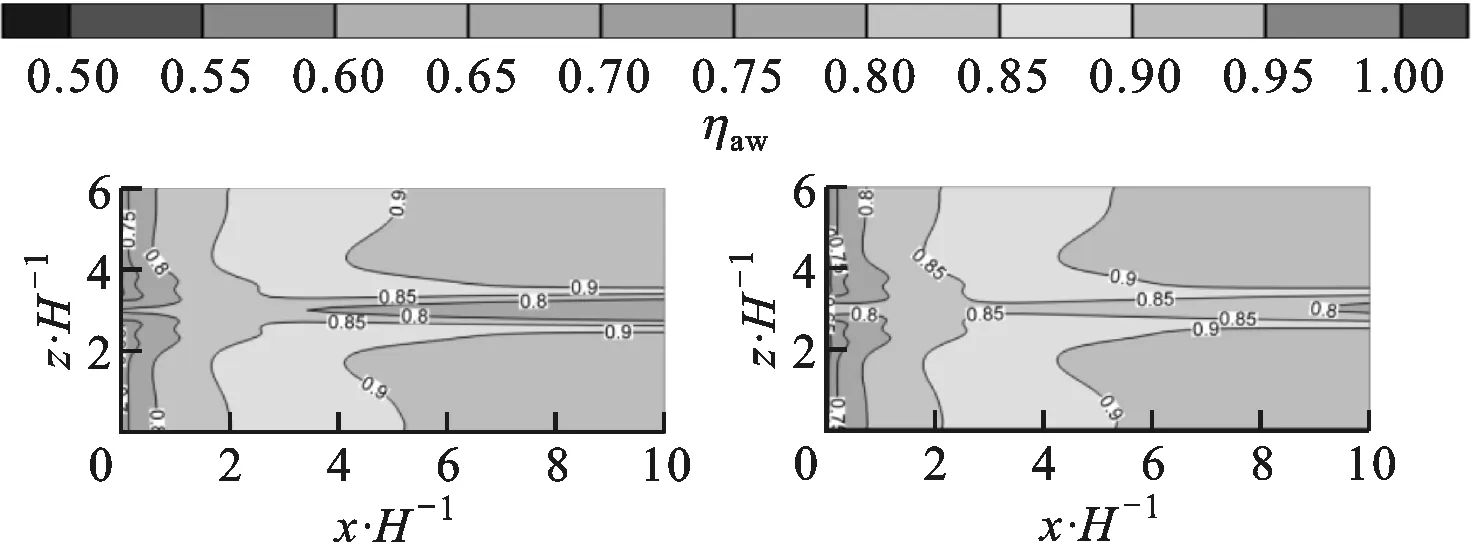
(a)t/H=0.25 (b)t/H=0.50

(c)t/H=1.00 (d)t/H=1.50图14 绝热壁面冷却效率分布
图15给出了能量损失系数及总压损失系数与唇厚的关系。从图中可以看到,能量损失系数及总压损失系数均随着唇厚的增大而增大。适当增加唇厚虽然可以使狭缝出口区域的冷却效率有所提升,但是要以较大的流动损失为代价。在实际设计过程中,通常需要根据叶片尾缘的具体结构来选取适当的唇厚,来满足冷却、流动、强度等方面的要求。

图15 损失系数与唇厚的关系
图16、17分别给出了M=0.8,不同唇厚结构的计算结果中,z/H=1和z/H=3这两个截面的温度比(T/Thg)和速度比(U/Uhg)的分布。从图16可知,唇厚的增大使冷、热气流开始混合的位置后移,但是对温度的整体分布规律以及热边界层的影响较小,只是增加了温度梯度的高度。因此,不同唇厚时,绝热壁面z/H为0~2和z/H为4~6之间区域的冷却效率分布规律基本一致。从z/H=3截面的温度比分布可以看到绝热壁面表面附近的低温区域显著增大,唇厚的改变主要影响了该位置附近的流场结构。

(a)z/H=1 (b)z/H=3图16 各截面温度比(T/Thg)分布
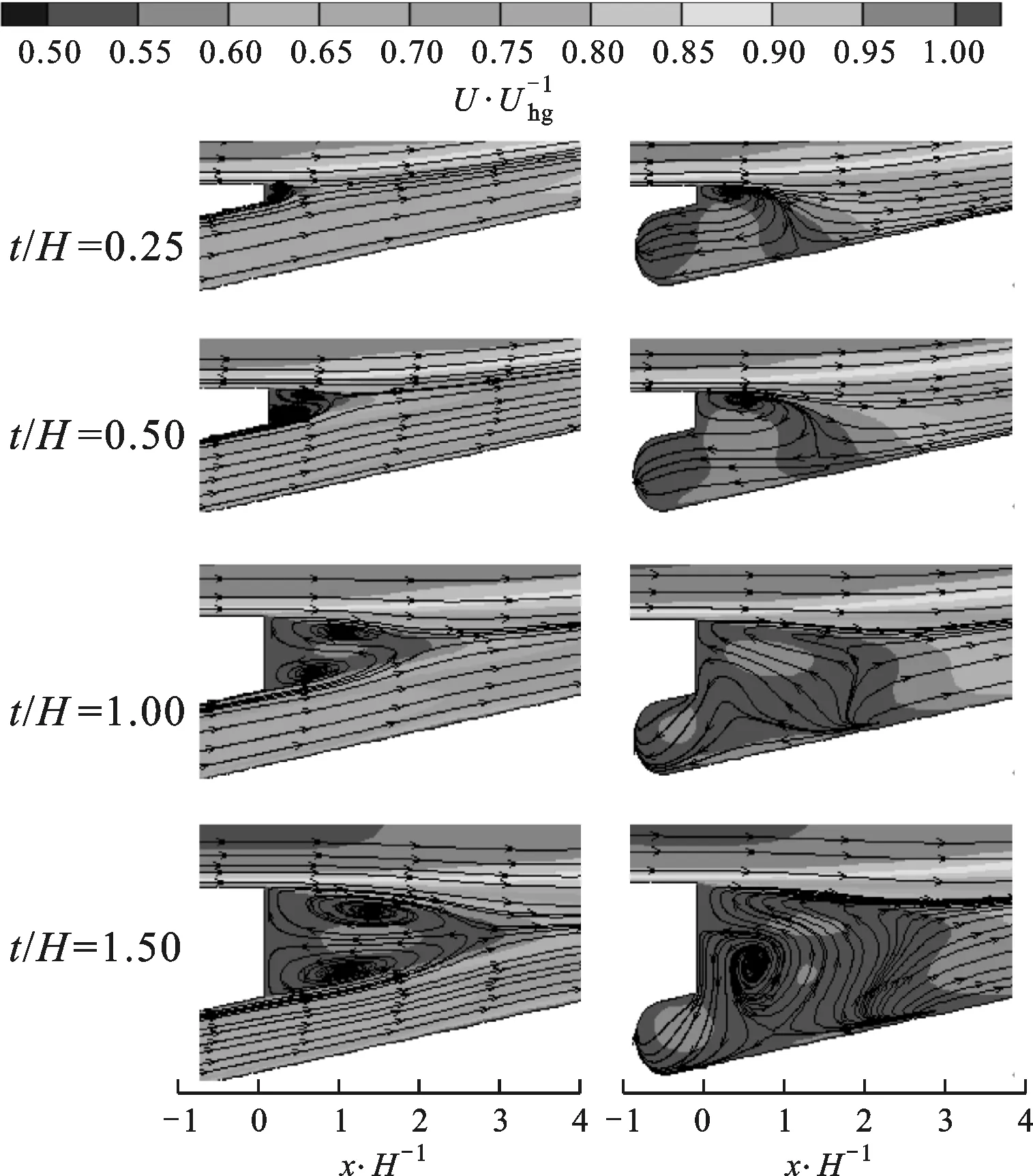
(a)z/H=1 (b)z/H=3图17 各截面速度比(U/Uhg)分布
从图17中可以看到,在z/H=1截面,主流流体和冷却气体高速流过台阶,并在台阶处形成了两个方向相反的旋涡。在肋柱背风面低压的驱动下,这两个旋涡在自身旋转的同时还会向肋柱附近逐渐移动。由于主流流速比冷却气体流速高很多,因此在出口台阶处形成的旋涡的流体主要来自冷却气体。唇厚的增大使得在狭缝出口台阶处形成的旋涡尺度增大,但是对绝热壁面附近的流场结构影响较小,因此不同唇厚时形成的热边界层相差不大。
图18给出了x/H=1截面的流线分布。从图中可以看到,z/H=1截面台阶处形成的两个旋涡发展至z/H=3截面附近时,下部的旋涡会脱离台阶向下游偏转,并与肋柱背风面形成的旋涡相互作用,形成更加复杂的流场结构。从图18中可以看到,z/H=3截面两侧各存在两个旋涡,由于台阶背风面区域气体流速很低,在两侧旋涡的作用下气流速度会稍微增大,因此在图17,z/H=3截面的速度比分布中,对应旋涡的位置出现局部高速区域。

图18 x/H=1截面流线分布
从图17,z/H=3截面的流线分布可以看到,唇厚的增大,使流场结构发生了显著变化。在t/H=0.25和0.5时,唇厚较小,主流流体的作用较强,在狭缝出口台阶处只存在一个由主流驱动形成的顺时针旋转的旋涡,冷却气体驱动产生的旋涡发生偏转向下游流动。唇厚的增大使得主流流体与冷却气体之间的距离增大,相互作用减弱。在t/H=1和1.5时,主流流体在台阶处的作用减弱,仅带动部分流体发生偏转流动,未形成明显旋涡。在t/H=1.5时,冷却气体驱动形成的旋涡得到充分发展,分出一部分气体向下游偏转流动后,在台阶处仍能保持着旋涡形式。在t/H=1.5时,由于流场结构的变化,所以绝热壁面上冷却效率分布的规律有很大不同。从图17可以看到,在绝热壁面x/H为1~2之间的区域仍然受x/H=2处旋涡反向流动的作用,但是在x/H为0~1之间的区域受到了来自台阶处旋涡的冲击作用,由于台阶温度较高,使得该区域冷却效率相对其他唇厚的计算结果较低。绝热壁面z/H为2.5~3.5,x/H>3的区域冷却效率主要受主流高温流体的影响。主流流体在肋柱背风面低压的作用下会更早作用到绝热壁面,引起冷却效率下降。唇厚的增大显著增大了主流流体与绝热壁面的距离,减弱了主流流体对绝热壁面的直接冲击。从图14中可以看到,绝热壁面z/H为2.5~3.5,x/H>3之间的区域,冷却效率随着唇厚的增大逐渐增大,冷却效果改善。
3 结 论
采用包含流体域和固体域的耦合传热数值求解方法,研究了压力侧开缝结构对典型燃气透平叶片尾缘冷却性能的影响,比较了与纯流体域计算结果之间的差异,研究了吹风比和唇厚对尾缘开缝出口区域冷却效果的影响,得到如下结论:
(1)当吹风比为0.5、0.8和1.1时,尾缘开缝结构内冷却通道的流量系数基本保持在0.7左右,能量损失系数基本保持在4%左右,主流总压损失系数分别为5.7%、5.3%和4.3%左右;
(2)与流体域、设置壁面温度恒定的计算方法相比,采用耦合传热计算方法、考虑流体与固体之间的耦合传热作用时,在高吹风比下可以更好地模拟狭缝出口区域冷却气流的温度场以及绝热壁面冷却效率的分布;
(3)增大吹风比可以有效增强冷却通道内的对流换热,改善开缝出口区域的气膜冷却效果,减少主流流体的总压损失,但是会增加冷却通道内的压力损失;
(4)开缝唇厚的增大使主流流体远离绝热壁面,由此减弱了主流流体对绝热壁面的直接冲击,改善了尾缘开缝出口区域的气膜冷却效果,但是会使能量损失和主流总压损失增大。
[1] HORBACH T, SCHULZ A, BAUER H J, et al. Trailing edge film cooling of gas turbine airfoils-effects of ejection lip geometry on film cooling effectiveness and heat transfer [J]. Journal of Heat Transfer, 2010, 41(8): 849-865.
[2] MARTINI P, SCHULZ A, WHITNEY C F, et al. Experimental and numerical investigation of trailing edge film cooling downstream of a slot with internal rib arrays [J]. Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy, 2003, 217(4): 393-401.
[3] TASLIM M E, SPRING S D, MEHLMANN B P, et al. An experimental investigation of film cooling effectiveness for slots of various exit geometries [C]∥26th AIAA/SAE/ASME/ASEE Joint Propulsion Conference. Reston, VA, USA: AIAA, 1990: 2266.
[4] HOLLOWAY D S, LEYLEK J H, BUCK F A, et al. Pressure side bleed film cooling: part 2 unsteady framework for experimental and computational results, GT2002-30472 [R]. New York, USA: ASME, 2002.
[5] AMES F, FIALA N, JOHNSON J, et al. Gill slot trailing edge heat transfer: effects of blowing rate, Reynolds number, and external turbulence on heat transfer and film cooling effectiveness, GT2007-27397 [R]. New York, USA: ASME, 2007.
[6] FIALA N, JASWAL I, AMES F, et al. Letterbox trailing edge heat transfer: effects of blowing rate, Reynolds number, and external turbulence on heat transfer and film cooling effectiveness, GT2008-50474 [R]. New York, USA: ASME, 2008.
[7] MARTINI P, SCHULZ A. Experimental and numerical investigation of trailing edge film cooling by circular wall jets ejected from a slot with internal rib arrays [J]. ASME Journal of Turbomachinery, 2004, 126(2): 229-236.
[8] MARTINI P, SCHULZ A, BAUER H J, et al. Film cooling effectiveness and heat transfer on the trailing edge cut-back of gas turbine airfoils with various internal cooling designs [J]. ASME Journal of Turbomachinery, 2006, 128(1): 196-205.
[9] MARTINI P, SCHULZ A, BAUER H J, et al. Detached eddy simulation of film cooling performance on the trailing edge cut-back of gas turbine airfoils [J]. ASME Journal of Turbomachinery, 2006, 128(2): 292-299.
[10]EFFENDY M, YUFENG Y, JUN Y, et al. Comparison study of turbine blade with trailing-edge cutback coolant ejection designs [C]∥51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA, USA: AIAA, 2013: 0548.
[11]徐虹艳, 张靖周, 谭晓茗. 涡轮叶片尾缘内冷通道旋流冷却特性 [J]. 航空动力学报, 2014, 29(1): 59-66. XU Hongyan, ZHANG Jingzhou, TAN Xiaoming. Vortex cooling performance in internal cooling channel of turbine blade trailing edge [J]. Journal of Aerospace Power, 2014, 29(1): 59-66.
[12]周超, 常海萍, 崔德平, 等. 涡轮叶片尾缘斜劈缝气膜冷却数值模拟 [J]. 南京航空航天大学学报, 2006, 38(5): 583-589. ZHOU Chao, CHANG Haiping, CUI Deping, et al. Numerical investigation of the cooling flow downstream of a turbine guide vane trailing edge slot [J]. Journal of Nanjing University of Aeronautics and Astronautics, 2006, 38(5): 583-589.
[13]王掩刚, 刘波, 姜健, 等. 涡轮叶片尾缘开缝喷气的数值模拟和试验研究 [J]. 航空动力学报, 2006, 21(3): 474-479. WANG Yangang, LIU Bo, JIANG Jian, et al. Experiment and numerical simulation investigation of turbine blade with trailing edge ejection [J]. Journal of Aerospace Power, 2006, 21(3): 474-479.
[14]王掩刚, 刘波, 曹志鹏. 喷气流与栅后流场掺混及干扰效应的探讨 [J]. 推进技术, 2002, 23(3): 223-225. WANG Yangang, LIU Bo, CAO Zhipeng. Mixing process in symmetry trailing edge slot for a turbine blade [J]. Journal of Propulsion Technology, 2002, 23(3): 223-225.
[本刊相关文献链接]
姚尔人,王焕然,席光.一种压缩空气储能与内燃机技术耦合的冷热电联产系统.2016,50(1):22-27.[doi:10.7652/xjtuxb201601004]
郭涛,管志成,孙光普,等.调频振子-液体联合水平减振的流固耦合机理研究.2016,50(1):28-33.[doi:10.7652/xjtuxb 201601005]
胡鹏,王伟,邓康耀,等.排气再循环与燃烧边界条件耦合对增压汽油机有效热效率的影响.2016,50(1):34-40.[doi:10.7652/xjtuxb201601006]
丁文俊,宋保维,毛昭勇,等.海洋动能发电装置在水下探测航行器的安装位置对发电性能的影响.2016,50(1):108-114.[doi:10.7652/xjtuxb201601017]
白浩,王伊卿,董霞,等.Ti6Al4V钛合金脉冲激光抛光微裂纹产生机理与尺寸特征研究.2015,49(12):117-123.[doi:10.7652/xjtuxb201512019]
宋明毅,吴伟烽,李直.汽车空调压缩机气阀运动规律模拟.2015,49(12):144-150.[doi:10.7652/xjtuxb201512023]
祝培源,郭振东,陈红梅,等.排汽缸全局气动优化及设计知识挖掘方法.2015,49(11):26-32.[doi:10.7652/xjtuxb2015 11005]
李彪,李黎川.新型磁链观测算法及其在永磁同步电机无位置传感器控制中的应用.2015,49(11):102-109.[doi:10.7652/xjtuxb201511017]
康乐,胡欲立,张克涵.水下磁谐振式无线电能传输系统的分析与设计.2015,49(10):41-47.[doi:10.7652/xjtuxb201510 007]
(编辑 赵炜 苗凌)
Numerical Investigations on the Cooling Performance of Trailing Edge Cutback in Gas Turbine Blade
GAO Yan,YAN Xin,LI Jun
(Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China)
A conjugate heat transfer method, which takes both the fluid and solid domains into consideration, was utilized to investigate the effect of pressure side cutback geometry on the cooling performance in a typical gas turbine blade. In order to validate the present numerical methods, the computed film cooling coefficient and pressure were compared with the experimental data. After the reliability and accuracy of the numerical method have been demonstrated, the influence of blowing ratio and lip thickness on the cooling performance was studied in detail. It shows that, among the selected three standardk-εturbulence model,k-ωturbulence model and SSTk-ωturbulence model, thek-ωturbulence model has superior accuracy in predicting the cooling performance of the blade trailing edge cutback. The conjugate heat transfer method considering both fluid domain and solid domain could properly resolve the temperature distributions near the cutback lip. As the blowing ratio increases, the convection heat transfer in the blade cutback channel is enhanced, and the corresponding film cooling coefficients are increased at the cutback outlet. If the height of the ejection slot is fixed, the scale of the vortices at the slot exit is increased with the increase of lip thickness. Such flow pattern reduces the impact effect of mainstream to the trailing edge cutback, which leads to a slight improvement of the overall cooling effectiveness at the cutback outlet region. However, the loss coefficient of the whole flow region is inevitably increased.
trailing edge cutback; conjugate heat transfer; blowing ratio; lip thickness
10.7652/xjtuxb201603005
2015-06-20。 作者简介:高炎(1991—),男,博士生;晏鑫(通信作者),男,副教授。
时间:2015-12-28
http:∥www.cnki.net/kcms/detail/61.1069.T.20151228.1956.002.html
TK11
:A
:0253-987X(2016)03-0029-09

