蒙特卡罗方法下线性模型的异方差性检验方法
王佐仁,徐生霞
(西安财经学院 a.统计学院;b.西安统计研究院,陕西 西安710061)
【统计理论与方法】
蒙特卡罗方法下线性模型的异方差性检验方法
王佐仁a,b,徐生霞a
(西安财经学院 a.统计学院;b.西安统计研究院,陕西 西安710061)
在已有的异方差性检验方法的基础上,运用蒙特卡罗方法,借助permutation检验思想,在不假定随机扰动项服从同一分布族的条件下,通过从大样本中提取大量的子样本,不断对线性模型进行拟合和检验,根据异方差为真的频率大小,给出了一种新的异方差检验方法。随机模拟表明本检验方法优于传统方法。
异方差性;蒙特卡罗;随机模拟;统计检验
一、引 言
总体的方差因总体不同而不同,即使是同一分布族,也会因总体不同而改变,即常常表现为异方差性。绝大多数统计方法,都是把同方差性作为前提条件,因此在应用这些统计方法时,必须注意到这个前提条件。否则,不考虑异方差性,套用这些统计方法,或许会得到虚假的结论。例如,回归模型的统计方法是对随机扰动项作了同方差的假定,用它研究中国家庭支出模式时,由于高收入人群对商品拥有更大的自由选择权,高收入家庭在购买商品的支出上,一般比低收入家庭的方差大[1]。如要套用现有的统计方法,其研究结论应当受到质疑。因此,在实际应用中,有必要对异方差的检验方法进一步探讨。
关于异方差问题的研究,除了古典的检验方法外,最早可以追溯到20世纪20年代,主要以国外学者为主,他们通过实例对统计模型中的随机扰动项存在异方差性的现象进行了总结和描述,得出了异方差的一些检验方法,如G-Q检验、布罗施-帕甘检验、怀特检验、Park检验、Glejser[2]51-80[3-6]检验等方法。国内学者主要集中在关于异方差不同检验方法的比较研究上[7]。
上述检验方法,丰富了统计理论,起到了奠基性的作用,但也有一定的局限性。如,G-Q异方差检验方法,是在随机扰动项为正态分布族且方差为单调型的情况下给出的。布罗施-帕甘异检验、怀特检验、Park检验、Glejser 检验是通过一次性检验对其存在性进行判断,结论存在着较大的误判风险。其次,所用到的随机模拟检验,没有给出确定的分析。另外, 假设条件仅仅停留在单一总体分布族的讨论上,至今还没有发现不同总体分布族条件下的研究成果。
理论上,线性模型含有普通参数、半参数,也含有随机参数和随机变量,模型的结构是复杂的[1]。模型中因变量的分布依赖于参数、半参数的取值及其随机参数和随机变量的分布。因变量的随机性只与随机扰动项有关的模型是一类比较简单的线性模型,在经济社会研究领域常被使用。本文在前人研究成果的基础上,针对这类线性模型,对其随机扰动项不作同一分布族的条件限制,运用蒙特卡罗随机模拟方法,借助Fisher在20世纪30年代提出的利用样本数据的全(或随机)排列,进行统计推断的permutation检验思想[8-10]。通过大量重复试验结果,依据频率大小,给出异方差的检验方法。
二、理论基础

(1)


根据定义,普通变量或向量X的取值可能是无穷的,对于X的无穷取值范围,一般情况下,理论上要证明这样的模型具有同方差性是不可能的,除非用此模型刻画的物理对象能够说明具有同方差性。既然如此,在理论研究中常常假定该模型具有同方差性,从而得出了完美的统计方法。而异方差性的证明反而容易一些,只要能够说明对于X的有限取值(如n个),随机扰动项εxi(i=1,2,…,n)的方差至少有两处不同就行了。
二十世纪四十年代,蒙特卡罗提出了一种统计随机模拟方法,其依据是频率收敛于概率的结论。即,设随机变量X的值域为I,对于任一波雷尔集I1,当P(X∈I1)=p时,若令:


三、异方差性的检验方法
关于只与随机扰动项εX有关的线性模型异方差检验方法讨论,本文将用多元线性模型进行总体概述,用一元线性回归模型进行具体阐述。
设(X1i,X2i,…,Xpi,Yi)(i=1,2,…,n)为容量为n的样本,于是可得:
Yi=β0+β1X1i+β2X2i+…+βpXpi+εi
(2)
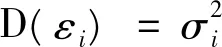
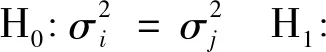
按照permutation检验思想,可用蒙特卡罗方法将已有的异方差检验方法进行优化。由于涉及到的检验方法比较多,且每种检验方法与permutation的嵌套思路一致,为了叙述方便,本文选择怀特检验进行叙述。
(一)异方差检验方法的优化


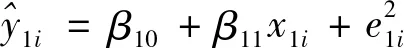

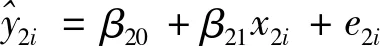

(二)多个线性模型异方差性的检验方法
按照一个线性模型异方差的检验思想,可以得到多个线性模型异方差性的检验方法。为方便起见,不妨用一元线性模型叙述。
设有n个一元线性模型,从第i个线性模型中得到一个容量为ni的样本(xij,yij),(j=1,2,…,ni;i=1,2,…,n),由此得到:
yij=βi+αixij+εij
(5)

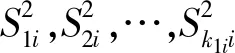



对于多个因变量的随机性只与随机扰动项有关的多元线性模型,同样按照本方法可以检验异方差性。值得指出的是,这些检验方法只适合在大样本情况下进行。在信息技术迅猛发展的时代,完全可以应用计算机技术,实施这些检验方法。
四、随机模拟
针对一元线性模型,将对上述提到的检验异方差的方法与传统的检验异方差方法在两种不同的情况下进行比较:一种是在同样的样本容量下,比较两种检验方法p值的大小;另一种是在同一个p值设定下,比较所需要的样本个数的多少。本文随机模拟的前提条件是在大样本情况下进行。
在R软件中生成一组均值为5,标准差为1的正态随机数(n=100);令方程为:y=8+0.7x+ε,并在R软件中产生一组没有固定规律的、容量为100的随机数作为随机扰动项的数据;(如图1所示,左图是随机扰动项的散点图,根据图形我们很难判断随机扰动项的分布及单调类型;右图表示的是x与因变量y之间的相关关系散点图)。
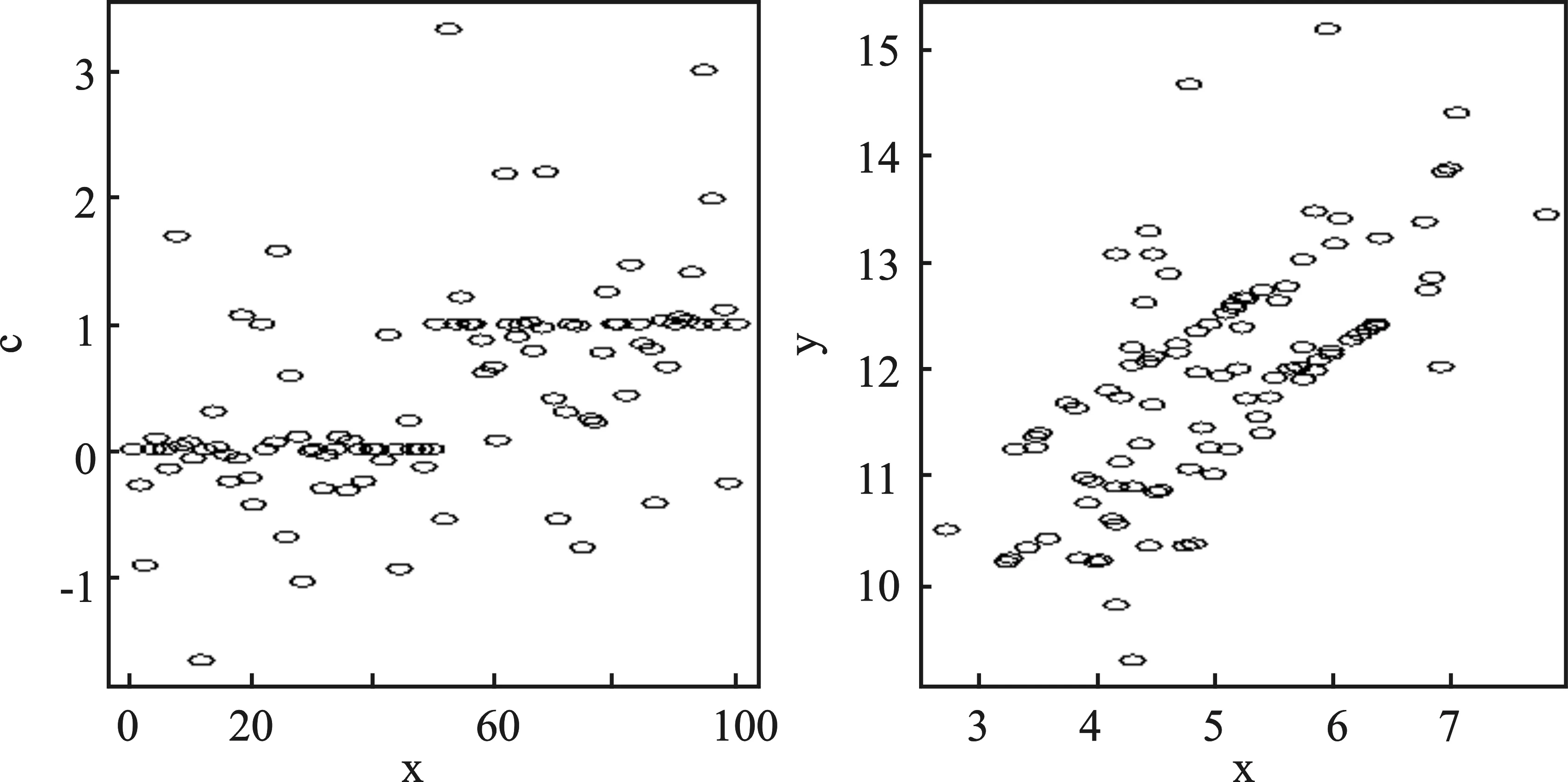
图1 散点图
根据右图,可以看出x,y之间存在一定的线性依存关系。对所得到的随机数据分别利用传统方法和新的异方差检验法进行10 000次的随机模拟,利用得到的p值来判断存在异方差的概率值。
经过模拟计算,结果为表1。从表1可以看出,相同样本容量下,新方法的p值为0.957,传统的检验方法p值为0.954,小于新方法下的值。另一方面,在同样的异方差性检验值p为0.95的情况下,所需要的样本容量存在差异,新方法的样本量为9 926,传统方法的样本量为9 958,新方法比传统方法需要的样本容量少22个。所以,随机模拟的结果表明,本文中所提出的异方差性检验方法是有效的。
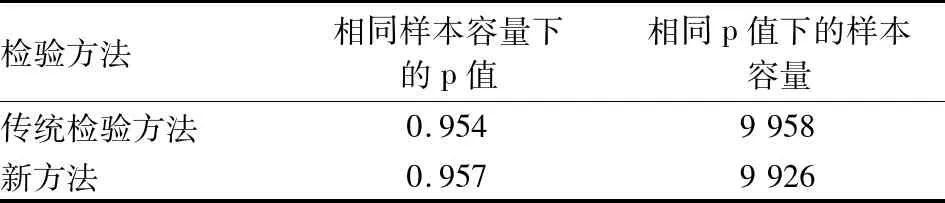
表1 两种检验异方差方法有效性的比较
五、实例分析
从股票市场上选择四个总体,分别为创业板块、深证综合板块、中小板块、上海综合板块。把2015年7月17日—2015年8月3日工作日期间每1分钟股票最高价和最低价作为指标变量,每个总体选择1 920个样本观测值,将对每一总体异方差性存在与否进行检验。
D1,D2,D3,D4分别代表创业板块、深证综合板块、中小板块、上海综合板块。X1,Y1分别代表创业板块的最低价与最高价;X2,Y2分别代表深圳综合板块的最低价与最高价;X3,Y3分别代表中小板块的最低价与最高价;X4,Y4分别代表上海综合板块的最低价与最高价;ε1,ε2,ε3,ε4分别代表四大板块模型中的随机扰动项。
根据实际数据,做因变量和自变量之间相关关系的散点图,对四个总体的模型选择做初步的判断,如图2。从图2不难看到,四大板块的变量间均呈现线性关系,部分一元线性回归模型分别如下:
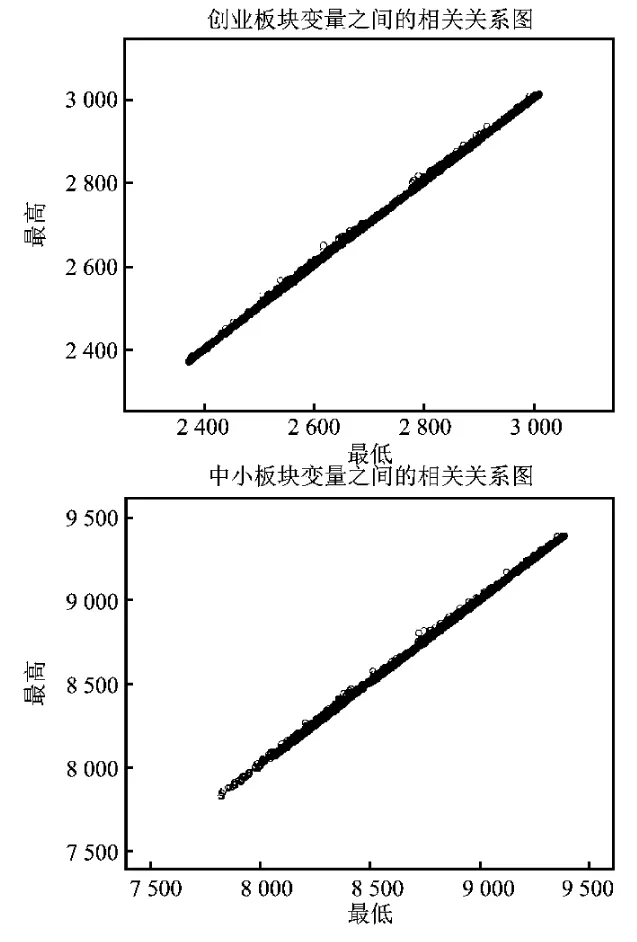
图2 板块变量间相关关系散点图
创业板块:Y1j=β1j+α1jX1j+ε1j
深证板块:Y2j=β2j+α2jX2j+ε2j
中小板块:Y3j=β3j+α3jX3j+ε3j
上海板块:Y4j=β4j+α4jX4j+ε4j
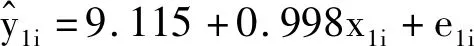


图3 创业板块残差与最低价之间的散点图
同理,对其余三个总体深证综合板块、中小板块、上海综合板块X2,X3,X4做异方差性检验,得到结果分别是:p2=0.007,p3=0.004,p4=0.008,认为随机扰动项也是存在异方差的。
六、结 论
在大样本条件下,对线性模型的随机扰动项不作条件限制,运用蒙特卡罗方法,借助permutation检验思想,通过在大样本中大量提取子样本,按照子样本数据,不断对线性模型进行初步的拟合和检验,根据异方差检验结果频率的大小,得出了一种新的随机扰动项异方差性的检验方法。这种方法只有当线性模型随机扰动项的异方差检验结果具有较高的频率时,才做出异方差为真的推断,降低了传统检验方法下用一次观察值得出检验结论的误判风险。但这种方法的不足之处是计算量大,需要借助于先进的计算工具,使用信息技术按照计算程序去完成。
[1] 王佐仁,杨琳.贝叶斯统计推断及其主要进展[J].统计与信息论坛,2012(12).
[2] 威廉 H 格林.计量经济分析[M].北京:中国社会科学出版社,1998.
[3] Breusch T S ,Pagan A R. A Simple Test for Heteroscedasticity and Random Coefficient Variation[J].Econometrica,1979,47(5).
[4] Park R E.Estimation with Heteroscedastic[J].Econometrica,1966,34(4).
[5] Stephen M Goldfeld, Richard E Quandt.Some Tests for Heteroscedasticity [J].Journal of the American statistical Association,1965,60(310).
[6] lejser H.A New Test for Heteroscedasticity[J].Journal of the American statistical Association,1969,64(325).
[7] 白雪梅.异方差性的检验方法及评述[J].东北财经大学学报,2002(6).
[8] 郁菁.回归模型异方差性的检验与消除研究———以SPSS为分析工具[J].长沙民政职业技术学院学报,2007(12).
[9] 尹增谦,管景峰,张晓洪,曹春梅.关于蒙特卡罗方法及应用[J].物理与工程, 2002(3).
[10]黄群,林洁梅,赵佳因.两个一维总体分布相等性的permutation 检验[J].辽宁工程技术大学学报:自然科学版,2012 (12).
(责任编辑:张爱婷)
Heteroscedasticity Testing Method by Linear Model Under the Monte Carlo Method
WANG Zuo-ren , XU Sheng-xia
(a.School of Statistics,b.Shaanxi Statistical Research Center; Xi'an University of Finance and Economics ,Xi'an 710061, China)
Existing Heteroscedasticity testing method is presented in this paper, on the basis of using the Monte Carlo method, with the help of a thought of permutation test, without assuming that submitting to the identically distribution family of the random disturbed term, through a large amount of extracted from large sample sample, constantly to fit linear models and inspection, according to Heteroscedasticity for really frequency size, put forward a new Heteroscedasticity testing method is given. Stochastic simulation shows that the test method is better than traditional methods.
Heteroscedasticity; Monte Carlo; stochastic simulation; statistical tests
2016-04-08;修复日期:2016-06-17
王佐仁,男,陕西乾县人,教授,硕士生导师,研究方向:抽样调查技术,随机过程及其应用; 徐生霞,女,硕士生 ,研究方向:抽样调查技术,随机过程及其应用。
F224.0∶O212
A
1007-3116(2016)11-0033-05

