非正态分布下具有自回归误差项的空间自回归模型变量选择研究
王周伟,陶志鹏,张元庆
(上海师范大学 商学院,上海 200234)
【统计理论与方法】
非正态分布下具有自回归误差项的空间自回归模型变量选择研究
王周伟,陶志鹏,张元庆
(上海师范大学 商学院,上海 200234)
将变量选择引入空间计量模型,讨论具有自回归误差项的空间自回归模型的变量选择问题。在残差非正态独立同分布的条件下,通过最大化信息熵,提出空间信息准则,并证明其在该模型变量选择中具有一致性。模拟研究结果表明:无论对单个系数还是对全部系数,空间信息准则都能很好识别,且与经典的赤池准则相比具有较大的优势。因此,空间信息准则是一种更为有效的变量选择方法。
空间计量分析;SARAR模型;变量选择;空间信息准则
一、引 言
在计量经济学实践中,随着信息技术的高速发展,研究者能够获得越来越多维度的信息变量,这使得在构建经济模型时,选用某种有效性判别方法确定哪些变量引入模型成为整个建模过程中比较关键的一步,这就是变量选择问题。早在20世纪70年代,Akaike基于信息论提出线性模型变量选择的赤池准则,也称为AIC准则(Akaike Information Criterion)。此后,学术界对此进行了广泛的后续研究:早期的研究主要集中在探讨构建经典线性模型时利用AIC准则选择变量的大样本统计性质[1-2],结果表明在一定条件下,AIC准则(或AIC准则的等价形式)在线性模型的变量选择中具有良好的大样本统计性质;进入21世纪后,学术界更为广泛地探讨了AIC准则在非经典线性模型中的拓展应用,如广义线性模型、联立广义线性模型等[3-5]。
然而,上述这些研究都没有考察变量之间的空间关系。随着新经济地理学的兴起,近30年来空间计量分析快速发展,已成为了主流计量经济学的一个重要分支而被广泛认可和接受[6],并在空间经济研究中也得到了广泛应用,如区域经济增长理论、税收理论等众多领域[7-8]。对于空间计量经济学理论的研究,学术界关注的焦点主要集中在模型的估计和检验[9-12],迄今为止国内外都很少有文献对空间计量模型变量选择问题进行研究。由于模型存在空间相关性(Spatial Dependent)从而Gauss-Markov假设不再成立,而经典线性回归中基于该假设构建的变量选择方法也随之失效,这就需要探讨经典变量选择方法能否以及如何扩展应用到空间计量经济模型中。此外,在实证应用中,由于空间相关性的存在,空间经济现象将更加错综复杂,被解释变量会受到更多因素的影响。所以,在构建空间计量模型时,为了减少遗漏变量所带来的偏差,学者们往往会引入众多解释变量。然而,在模型中加入大量无关紧要的变量又会对模型估计精度和可靠性产生很大的负面影响,这就需要一种方法解决空间计量经济模型的变量选择问题。
在空间计量模型中,目前较为常用也是最为基础的模型是具有自回归误差项的空间自回归模型(Spatial Autoregressive Model with Autoregressive Disturbances,SARAR模型)。为解决SARAR模型的变量选择问题,在残差非正态独立同分布的条件下,本文将推导出经典AIC准则的空间形式,即空间信息准则(Spatial Information Criterion,SIC)。
二、SARAR模型的变量选择问题
SARAR模型把被解释变量和误差项的空间相关性同时引入模型,是更加一般的空间模型,最早由Kelejian和Prucha提出。设n维向量y=(y1,y2,…,yn)′为被解释变量,xj=(x1j,x2j,…,xnj)′为候选解释变量,其中j=1,2,…,p*其中p为有限值,讨论问题均要求p<∞,对于p→∞这一理论上存在的情形,本文不进行分析。,解释变量矩阵为X=[x1,x2,…,xp],SARAR模型如下所示:

(1)

记{1,2,…,p}的幂集M为指标集,对于任意α={j1,j2,…,jp(α)}∈M对应的模型,候选解释变量矩阵为X(α)=[xj1,xj2,…,xjp(α)]。为了表示方便,在下文中将该候选解释变量集称为变量集α,参数θα的拟极大似然估计量如下所示:
令P(λα)=In-λαW1,Q(ρα)=In-ραW2,In是一个n×n的单位矩阵,中心化对数似然函数为:
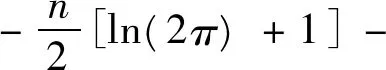
(2)
其中
(3)
其中‖‖为欧式范数,M(α)=In-Q(ρα)X(α)[X′(α)Q′(ρα)Q(ρα)X(α)]-1X′(α)Q′(ρα),对于式(2),其得分函数为:
(4)

(5)
其中
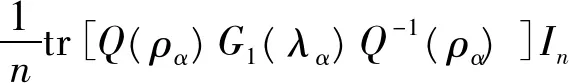
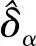
(6)
在此基础上,βα的拟极大似然估计量为:

(7)
进而,对于被解释变量的估计为:
(8)
三、SIC准则及其变量选择的大样本统计性质讨论
(一)SIC准则
对于候选解释变量集与α*之间的差异,本文采用Kullback-Leibler距离进行度量。对于任意的α∈M与α*之间的距离为:
(9)
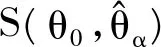
(10)
由式(9)(10)可知,SARAR模型的变量选择过程实质上就是最大化信息熵,或最小化Kullback-Leibler距离,这与Akaike提出的AIC准则类似。但是,由于空间相关性的引入,基于线性模型的AIC准则不再成立。对于SARAR模型的变量选择问题,本文将AIC准则推广为SIC准则,具体可以概括为命题1。

其中K=p(α)+3,K为未知参数空间的维数,p(α)为变量集α中解释变量的个数。
证明:以下利用最大熵原理进行证明命题1,即:

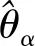


(11)
又由于ln(•)单调递增,从而式(11)可以化简为:
综上,命题1得证。


在具体的变量选择过程中,首先将解释变量标准化以去除量纲,将被解释变量中心化以保证截距项为0。在算法实现中,可以将逐步AIC方法[13]进行推广为逐步SIC方法,具体包括前向法和后向法。若SIC准则对于SARAR模型的变量选择过程是一致的,则两者是等价的,一致性证明将在下文中给出。
(二)基于SIC准则的SARAR模型变量选择的大样本统计性质
本部分将采用统计决策论方法,对SIC准则在SARAR模型变量选择过程中的大样本统计性质进行探讨。为了对SIC准则的有限性进行测度,本文采用式(12)所示的损失函数:
(12)
将式(8)带入式(12)得:
L(α)=
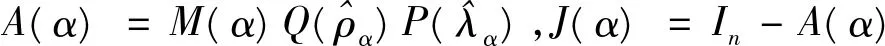

(13)
这里Eα[•]表示基于α求期望。

为了对命题2进行证明,首先证明引理1引理2成立。
引理1证明:由式(3)得:
(14)
(15)
又由于ln(•)单调递增,从而式(15)与SIC准则等价,引理1得证。
引理2:在命题2的条件下,以下等式成立:
(16)
其中op[L(α)]表示L(α)在概率测度下的高阶无穷小量。
引理2证明:将式(3)式(12)带入Γ(α)得:
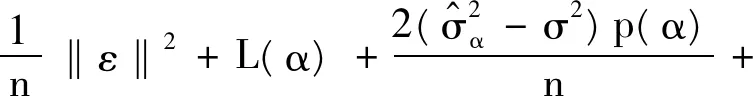
(17)
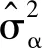
(18)
由切比雪夫不等式可知,对于任意的γ1>0,有:
(19)

(20)
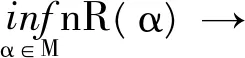
(21)


(22)
另一方面,由式(12)式(13):
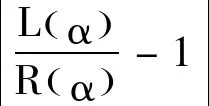


(23)
由式(18)、(21)、(22)、(23),引理2得证。
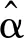
四、基于SIC准则的变量选择效果模拟研究
以下通过Monte Carlo模拟对SIC准则的有限样本性质进行研究,样本数据由式(24)所示的模型生成:
y=λW1y+x1β1+x2β2+x3β3+x4β4+ (In-ρW2)-1ε
(24)

(25)
其中r为候选解释变量之间的相关性,r越接近1,则表明候选解释变量之间的相关替代性就越强,即候选变量之间存在共线性的问题。为了反映其变量选择结果的影响,分别设定r为0.25和0.85,代表不存在共线性和存在共线性的两种情况。
Monte Carlo模拟通过R3.2.4编程实现,采用前向法进行SIC准则变量选择,样本量分别取n=60、100、200、500,重复1 000次。为了研究本文提出SIC准则在有限样本下变量选择的表现,分别计算识别系数1、-0.5、0.1、0时的概率,分辨所有非零系数的概率(选中所有关键变量的概率)记为p1以及分辨所有系数的概率记为p2。
作为比较,本文还采用传统的AIC准则进行变量选择,并对相关结果进行计算,模拟结果见表1。

表1 不同准则下SARAR模型变量选择结果比较表
从表1中可以看出:
第一,在残差非正态条件下,对于SARAR模型的变量选择,无论对单个系数还是对全部系数,本文提出的SIC准则都能很好识别,且随着样本量的增加,识别效果随之提升。
第二,总体而言,SIC准则的识别效果明显优于AIC准则。当系数明显非零时(系数为1和-0.5),SIC准则和AIC准则都能很好识别;而当系数为不明显的非零数时(系数为0.1),SIC准则显著优于AIC准则,即SIC准则可以明显降低错选变量的概率,且当残差的方差较大、变量间相关系数较大时,SIC准则更加具有优势。
第三,方差以及变量之间的相关系数都会对SARAR模型变量选择的效果产生影响。当方差和相关系数都越小,SIC准则的选择结果越精确。
五、总 结
本文讨论了SARAR模型在残差非正态独立同分布条件下的变量选择问题,提出了一种新的SIC准则,并对其大样本统计性质进行了讨论。该准则可以看作AIC准则从线性模型到空间模型的推广。模拟结果表明:与AIC准则相比较,SIC准则在空间模型的变量选择过程中更具优势;值得一提的是,SIC准则基于较为一般的空间模型,且只要求残差独立同分布,这就使SIC准则的适应条件更加宽泛,且更符合经济现实。
[1] Li K. Asymptotic Optimality for Cp, CL, Cross-Validation and Generalized Cross-Validation: Discrete Index Set[J]. The Annals of Statistics, 1987,15(3).
[2] Shao J. An Asymptotic Theory for Linear Model Selection[J]. Statistica Sinica, 1997,7(2).
[3] Yanagihara H, Kamo K, Imori S, et al. Bias-corrected AIC for Selecting Variables in Multinomial Logistic Regression Models[J]. Linear Algebra and its Applications, 2012,436(11).
[4] Kamo K, Yanagihara H, Satoh K. Bias-Corrected AIC for Selecting Variables in Poisson Regression Models[J]. Communications in Statistics: Theory & Methods, 2013,42(11).
[5] Wang D R, Zhang Z Z. Variable Selection in Joint Generalized Linear Models[J]. Chinese Journal of Applied Probability and Statistics, 2009,25(3).
[6] Anselin L. Thirty Years of Spatial Econometrics[J]. Papers in Regional Science, 2010,89(1).
[7] 汪辉平, 王美霞, 王增涛. FDI、空间溢出与中国工业全要素生产率——基于空间杜宾模型的研究[J]. 统计与信息论坛, 2016(6).
[8] 龙小宁, 朱艳丽, 蔡伟贤, 等. 基于空间计量模型的中国县级政府间税收竞争的实证分析[J]. 经济研究, 2014(8).
[9] Kelejian H H, Prucha I R. A Generalized Spatial Two-Stage Least Squares Procedure for Estimating a Spatial Autoregressive Model with Autoregressive Disturbances[J]. The Journal of Real Estate Finance and Economics, 1998,17(1).
[10]Lee L. Asymptotic Distributions of Quasi-Maximum Likelihood Estimators for Spatial Autoregressive Models[J]. Econometrica, 2004,72(6).
[11]Yang Z. LM Tests of Spatial Dependence Based on Bootstrap Critical Values[J]. Journal of Econometrics, 2015,185(1).
[12]周少甫, 白羽. 空间面板杜宾模型的Bootstrap Wald-COMFAC检验研究[J]. 统计与信息论坛, 2016(5).
[13]Yamashita T, Yamashita K, Kamimura R. A Stepwise AIC Method for Variable Selection in Linear Regression[J]. Communications in Statistics-Theory and Methods, 2007,36(13).
[14]Whittle P. Bounds for the Moments of Linear and Quadratic Forms in Independent Variables[J]. Theory of Probability and Its Applications, 1960,5(3).
(责任编辑:郭诗梦)
Research on Variable Selection in Spatial Autoregressive Model with Autoregressive and Non-Normal Disturbances
WANG Zhou-wei, TAO Zhi-peng, ZHANG Yuan-qing
(School of Finance and Business, Shanghai Normal University, Shanghai 200234, China)
Introducing variable selection in spatial model, we consider how to select variable in Spatial Autoregressive Model with Autoregressive Disturbances. Based on the assumption that the residuals are independently and identically distributed, we obtain Spatial Information Criterion(SIC) by minimizing information entropy.We prove the selection consistency of the introduced criteria and evaluate their performance by Monte Carlo simulation.The results suggest that no matter for one or for all coefficients, they can be recognized by SIC. What's more, SIC is better than AIC for the variable selection of spatial model. Therefore, SIC is a much efficient one.
spatial econometrics analysis;SARAR model;variables selection;SIC
2016-03-08;修复日期:2016-07-16
国家自然科学基金项目《基于流动性视角的资产定价模型重构研究》(71471117);教育部人文社会科学研究青年基金项目《变系数空间面板数据模型变量选择方法及应用》(15YJC790150)
王周伟,男,山西闻喜人,博士后,教授,研究方向:金融管理,数量经济; 陶志鹏,男,陕西咸阳人,硕士生,助理研究员,研究方向:空间计量,变量选择; 张元庆,男,山东济宁人,数量经济学博士,副教授,研究方向:空间计量,变量选择。
F224.0∶O212.1
A
1007-3116(2016)11-0027-06

